測速應答機相位誤差分析及精度提升方法

葉 雷，李忞詝，梁琴琴，崔穎升

(上海航天電子技術研究所，上海 201109)

0 引言

在現代測控系統當中，多采用測速應答機配合地面基站實現高精度的多普勒測速功能[1-3]，由于下行載波頻率需與上行載波頻率滿足固定轉發比進行相參轉發，因此相參轉發的方法是整機設計時需要重點考慮的因素之一[4-5]。近年來，隨著大規模現場可編程門陣列(Field Programmable Gate Array，FPGA)、數字信號處理(Digital Signal Processing，DSP)等數字技術的應用及發展，具有通用化、數字化和小型化等特點的測速應答機逐步設計實現，應答機呈現出新的發展趨勢[6-10]。

近期，面向整體的多路相參轉發數字應答機設計方法[11-12]被提出，該方法可實現多路信號轉發應答機需求。采用數字中頻拓展、通道共用的方法，省略了傳統的中頻頻變過程，精簡了系統流程。同時結合FPGA、數字鎖相環(Digital Phase Lock Loop，DPLL)等進行數字信號處理的方法[13-15]，實現應答機的數字化、軟件化。

為了進一步提高數字測速應答機的精度和可靠性，需要對應答機系統中的各個參量進行細化分析[16-18]。其中，相參轉發信號相位誤差是直接影響其高精度測速性能的因素之一，該因素不僅與系統中采用的數字鎖相環路有關，還受到系統軟硬件多方面性能和參數的限制[19-23]。

本文基于相參轉發數字測速應答機，理論分析了影響數字測速應答機轉發信號相位誤差的多個因素，給出了限制轉發相位精度的關鍵參數。分析指出，數字測速應答機在數字信號處理過程中使用的數字鎖相環、轉發比、直接數字頻率合成器(Direct Digital Synthesizer，DDS)[24]等模塊參數的量化誤差是相參轉發相位誤差的主要來源，進而提出一種在中頻轉發信號時合理提高變量位寬，從而提升數字測速應答機相位精度的方法。結合硬件元器件精度指標以及軟件資源占用率，通過定量計算選取最優位寬，并指出了進一步提升性能的可行方案，為現有測速應答機系統的設計提供了理論借鑒。

1 相參轉發數字測速應答機

相參轉發測速應答機目前多采用固定本振相參轉發方式[25-26]，直接根據轉發比ρ轉發中頻信號，為同時滿足轉發信號頻率fT=ρfR及fIT=ρfIR，可得到轉發比ρ=(MT2-MT1)/(MR2+MR1)，頻率流程如圖1所示。通過集成設計方法[11]，選取合適的值滿足MT2=MR2，MT1=MR1,可以實現數字應答機收發本振的共用，得到應答機更為簡化的轉發方式。

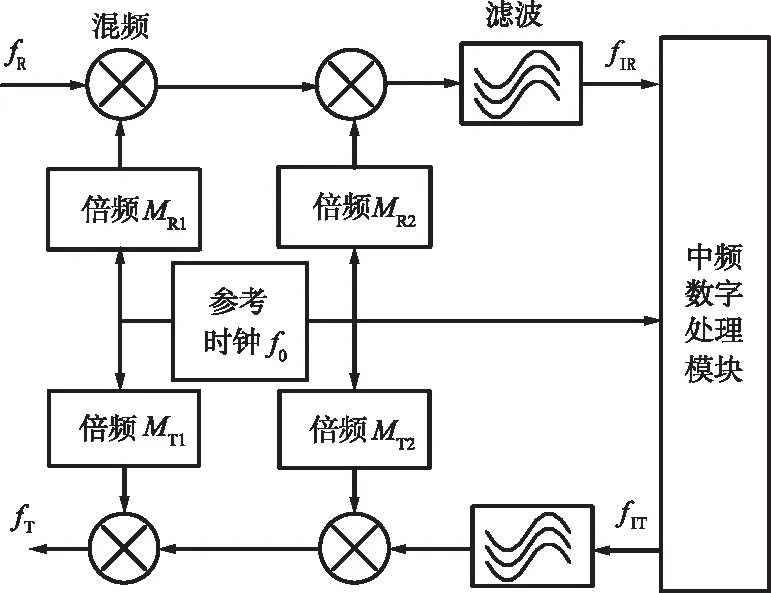
圖1 固定本振相參轉發頻率流程Fig.1 Flow chart of coherent transponder with fixed local oscillator

在中頻數字處理模塊中，使用DDS技術[11]在FPGA芯片內實現信號的相參轉發，DDS主要由頻率控制字、相位累加器和波形存儲器組成，在參考時鐘的驅動下，相位累加器對頻率控制字進行累加，得到相位碼對波形存儲器尋址，波形存儲器輸出相應的幅度碼。該技術具有頻率切換速率快、分辨率高以及易于實現等優點，目前已廣泛應用于通信、雷達和航空航天等領域[4]。

2 相位誤差分析

在基于相參轉發體制的數字應答機中，系統捕獲信號后，應答機生成的相應轉發信號已與接收信號相參鎖定，轉發信號的相位信息具有連續性，不存在相位翻轉、跳變等情況。此時，該轉發信號的相位信息可通過轉發頻率以及初始相位信息表示，因此對轉發信號的相位誤差分析可由轉發信號的頻率精度分析入手。對于一般的數字應答機，轉發頻率誤差來自于軟件與硬件2個方面。軟件方面，中頻轉發信號由數控振蕩器(Numerically Controlled Oscillator，NCO)生成，其頻率誤差由輸入NCO的頻率控制字精度決定；而硬件方面，頻率誤差主要取決于系統采用晶振的短期穩定度能力，該指標影響到頻率源在對信號進行下/上變頻時刻的瞬時相位差。目前，晶振的10 ms短穩指標多優于1×10-11。在環路跟蹤狀態下，信號的收發時延在ms量級，短穩造成的瞬時相位差相對于FPGA數字量化誤差可以忽略。因此，數字應答機的轉發相位誤差主要來自于軟件方面的頻率數字量化誤差。

2.1 中頻相參轉發

測速應答機的數字中頻相參轉發原理如圖2所示。

圖2 中頻相參轉發原理Fig.2 The principle diagram of midfrequency coherent transponder

經歷了下變頻后的中頻接收信號通過由數字鑒相器、環路濾波器和數控振蕩器構成的全數字鎖相環進行相位跟蹤，相位鎖定后，環路濾波器輸出與接收信號相參的頻率控制字，此時通過中頻信號轉發比ρ可對該頻率控制字進行縮放，得到需要的中頻轉發信號頻率控制字，最終獲取的頻率控制字再輸入到數控振蕩器中生成中頻轉發信號進行輸出。

2.2 轉發誤差分析

在鎖相環結構中，當接收信號相位被鎖定時，輸入信號和接收鎖相環輸出信號的頻率誤差被限制在一定范圍內，若其中的環路濾波器階數較高，其帶來的頻率誤差很小，相比于環路數控振蕩器輸出的頻率誤差而言可忽略不計。對各個信號進行量化之后，系統的轉發頻率誤差受限于各參數量化后的最小頻率分辨率。實際轉發過程中，對信號進行的轉發計算以及截位等運算都是通過對應頻率控制字進行計算得到。在各參數量化之后，中頻轉發信號fIT可表示為：

(1)

式中，ρ為量化后的轉發比；fclk為本振時鐘信號；KPLL為信號鎖定后接收鎖相環輸出頻率控制字；bDDS為DDS輸出位寬。

在理想情況下，各參數為量化值加上對應量化誤差。通過DDS輸出中頻轉發頻率時，輸出頻率為：

(2)

式中，KIT為轉發輸出信號頻率控制字；εDDS為輸出頻率量化引入誤差。

對照組患者主要結合病患實際情況給以常規藥物治療，如：鈣通道拮抗劑、硝酸、依那普利等藥物，若血壓高的患者還要配以心得安、利血平、氫氧噻嗪等降壓藥物，同時注意飲食健康，確保低脂低鹽飲食；觀察組患者在上述常規治療的基礎上增加纈沙坦藥物治療，80 mg/次，1次/d。在加入纈沙坦治療的過程中，需要根據患者身體情況（如血壓是否正常、是否有不良反應等），每周進行藥量調整，藥量盡量控制在40～160mg/次，若患者一切正常則可以繼續使用纈沙坦治療。

在信號轉發計算過程中，數字量化會導致無法實現嚴格的轉發比，記轉發比誤差為ερ，結合環路振蕩器數字量化引入的鎖定誤差εPLL，在信號鎖定之后得到的轉發信號頻率控制字如下：

(3)

結合式(1)～ 式(3)可計算出輸出信號誤差ε=fIT0-fIT，即：

(4)

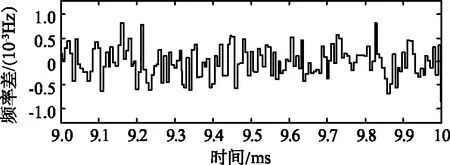
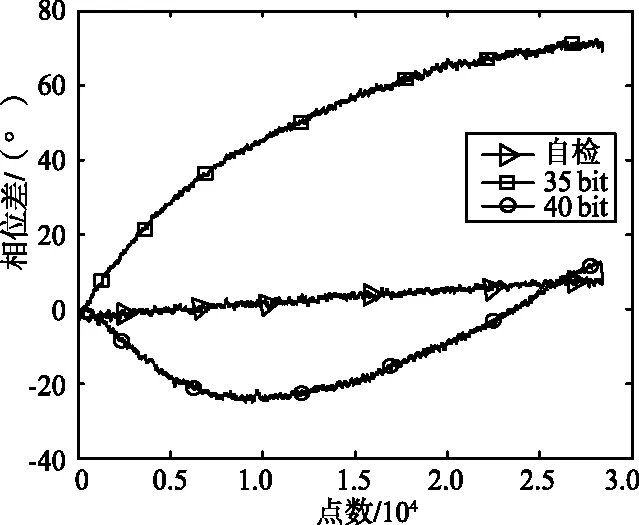
由于bDDS+n=bPLL+bρ，lb(KPLL)

(5)

3 相位精度提升

根據式(5)不難發現，在設計測速應答機數字信號處理過程中，通過提高相參轉發過程中的各參數頻率量化的精度，從而使得相位精度也獲得相應的提高。當本振時鐘頻率fclk確定時，轉發信號的相位誤差主要與接收鎖相環相位精度、轉發比以及輸出信號頻率的量化誤差有關。

在實際應用中，頻率源元器件的穩定度指標也會影響轉發信號相位精度，因此，在相參轉發數字信號處理中，在滿足技術指標要求情況下，增加接收信號鎖相環、轉發比以及輸出信號DDS變量的位寬可以有效降低轉發信號的相位誤差，提高轉發精度；當轉發精度高于頻率源元器件穩定性時，繼續提高變量位寬并不會優化應答機轉發信號相位精度，反而會消耗軟件資源，增加軟件資源占用率。

考慮當fclk=100 MHz時，若上述所有位寬相等，則轉發的頻率和相位隨位寬的變化如圖3(a)和圖3(b)所示。可以看到，轉發頻率和相位誤差與位寬在對數單位下呈現線性關系，若需要轉發相位精度小于0.01°/s，位寬至少需要38 bit才能滿足。

(a)轉發頻率誤差隨位寬變化

(b)相位誤差隨位寬變化圖3 轉發頻率誤差和相位誤差隨位寬變化Fig.3 Transmit frequency error and phase error vary with bit width

根據實際設計產品指標，目前晶振短穩指標可達1×10-11/10 ms，在100 MHz主時鐘條件下得到晶振的頻率誤差為10-3Hz。根據式(5)可以得到，在鎖相環以及輸出DDS的位寬為38 bit時，系統的相位誤差為0.001 Hz，故在FPGA資源利用率最小的情況下，取鎖相環及DDS位寬為38 bit即可使系統轉發信號的相位誤差主要受限于頻率源穩定度指標。

3.1 仿真驗證

輸入信號與NCO輸出信號的頻率差如圖4所示，該誤差在4 ms后已經衰減到一個很小的量。在后端的局部放大可以發現，其頻率誤差已經被抑制在10-3Hz量級，滿足上述誤差要求。

(a) 輸入信號

(b) NCO輸出信號圖4 輸入信號與NCO輸出信號的頻率差Fig.4 The frequency difference between input signal and NCO output signal

3.2 試驗驗證

根據上述分析設計數字中頻處理軟件，結合數字雙頻連續波應答機產品對信號轉發精度進行測試驗證。在產品軟件設計中，結合式(5)可得環路振蕩器頻率、DDS輸出頻率以及轉發比量化位數在超過34 bit時可滿足相位誤差≤10°/s的設計指標，由于實際測試中存在信號源不穩定、噪聲等設備因素、環境因素對應答機轉發相位誤差造成的影響，設計取35 bit可滿足指標要求。同時根據晶振短穩指標計算得到，在鎖相環以及輸出DDS的位寬為38 bit時，系統的相位誤差為0.001 Hz，與晶振短穩指標相當，為驗證上述理論分析，進一步增加2 bit以避免其影響。故使用綜合測試儀分別試驗驗證了環路振蕩器頻率、DDS輸出頻率以及轉發比量化位數在取35，40 bit兩種情況下，接收到的轉發信號與輸出信號間的相位長期漂移，試驗結果如圖 5所示，測試時間為100 min。

由圖5可以看出，在加電100 min后，測試設備在自檢狀態下的相位差，設備自身的信號轉發模式會產生7.17°的相位漂移；在量化位數取35 bit時，加電100 min會產生71.21°的相位漂移，隨機誤差為4.105°；在量化位數取40 bit時，最大相位漂移為36.82°，隨機誤差為4.028°。通過對比可發現，在不考慮設備自身信號長期相位漂移的情況下，在提高環路振蕩器頻率、DDS輸出頻率以及轉發比量化位數之后，系統轉發信號的相位誤差有明顯改善，長期漂移從0.011 9°/s減少至0.006 1°/s，降低48.739%。

圖5 轉發信號長期相位漂移Fig.5 The long term phase shift of transmitting signal

同時對轉發信號頻率穩定度進行了計算，如表1所示。在加電測試80 min情況下，頻率穩定度從0.025 8°/s降至0.023 2°/s，提高了10%，得到更高的轉發精度。

表1 轉發頻率穩定度Tab.1 Stability of forwarding frequency

若需進一步確保轉發相位精度，需要對數字鎖相環路的相位誤差進行控制。研究表明，在被跟蹤目標為高動態情況，即多普勒頻率變化率較大的情況下，取階數為二階的鎖相環在對目標進行跟蹤時會存在一個不能忽略的相位誤差，該誤差會導致測速時引入較大誤差。為進一步提高測速應答機跟蹤能力以及加速度性能，可考慮提高環路濾波器階數的方法。

4 結束語

本文以測控系統中使用的高精度測速應答機為背景，通過對相參轉發數字信號處理模塊中的中頻轉發流程進行分析，提出一種提高鎖相環路NCO以及輸出DDS變量位寬的方法，可以降低相位誤差，提高轉發精度。仿真結果表明，信號轉發位數提高1位，能提高轉發頻率精度3.01 dBHz，當變量位數提高至38 bit時，應答機轉發信號的相位誤差與晶振穩定度指標相當。在實際應用過程中根據資源占用率及元器件性能進行綜合考慮、選取合適位數進行數字信號處理，可以有效降低相位誤差，提高轉發精度。通過在工程應答機上進行對比驗證發現，將位數從35 bit提高至40 bit可以降低轉發信號的系統誤差約48.3%，頻率穩定度提高10%，該方法對于應答機設計有一定的工程實用價值。