一種適用于高動態的高精度頻率估計方法

馬立波 ，陳敬喬

(1.北京跟蹤與通信技術研究所，北京 100094；2.中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

伴隨社會的發展和信息時代的到來，以0,1傳輸的數字無線通信已是當今主要的信息傳遞方式，廣泛應用于各種場景[1]。無線傳輸信道和數字收發設備本身的不確定性對數字通信的可靠性提出了挑戰，其中收發兩端設備間的頻率偏移就是嚴重影響數字通信性能的問題之一，嚴重時將阻斷通信[2]。所以，如何在接收端有效估計接收數據的頻率偏移量，成為保障通信穩定可靠的關鍵[3]。

在任何數字接收端都有配套的硬件設備，由于系統中使用的頻率源精度有限，由其產生的用于正交數字下變頻的本地振蕩信號是一個固定頻率的自由振蕩信號，且在實際應用中受到各種因素的影響，其實際輸出頻率與理想頻率之間存在差異，該本振信號的頻率不可能和輸入信號的載波頻率完全一致，由此必然會產生頻差[4]。另一方面，如果接收機處于移動狀態，由于相對運動產生的多普勒效應將導致接收機接收到的信號載波頻率與所發射信號載波頻率之間存在一定的偏差，即多普勒頻移[5]。當發射機與接收機相對運動且彼此接近時，接收機所收到的信號頻率將高于發射信號的頻率；而當發射機與接收機相對運動且彼此遠離時，接收機收到的信號頻率將低于發射信號的頻率，即多普勒效應[6]。

隨著高速鐵路、高速公路和低中軌衛星等移動通信業務的發展，高動態場景下的無線移動通信應用需求與日俱增，不再局限于簡單的話音通信，視頻、圖像及移動互聯網等高速數據傳輸已成為當前的迫切需要[7]。但是，高動態場景的移動通信信道條件更為復雜多變，尤其是收發雙方相對運動速度快，不可避免產生大的多普勒頻移，加深了系統碼間串擾，降低接收端解調性能，嚴重影響系統傳輸的可靠性[8]。目前接收端對數據頻偏估計的范圍和精度相互矛盾，二者難以同時滿足要求，如何在保證頻率估計范圍情況下進一步提高估計精度是實現穩定可靠的高動態無線移動通信亟待解決的問題。

實現頻率估計的方法可以分為兩大類：以硬件電路為基礎的測頻法和以離散傅里葉變換為基礎的頻譜分析法[9]。前者通過硬件電路檢測信號波形估計頻率，受噪聲影響較大，難以適應高精度要求，且成本較高；后者因FFT提高了運算速度而得到廣泛應用，其估計精度主要取決于采樣率和數據長度[10]。目前，實際應用的頻率估計方法多是基于FFT，文獻[11-17]介紹了FFT的多種變形和改進，主要是在離散傅里葉變換基礎上進行譜細化同時改善計算復雜度的算法設計。多普勒頻移對通信系統產生嚴重影響，降低接收端同步和解調性能，為解決多普勒頻偏問題，有多種方式可以選擇，其中應用最為廣泛的開環頻率估計方法是最大似然估計。Rife首先提出了采用周期圖譜估計單音信號頻率的方法，具有估計精度高、抗噪聲能力強等優點，然而計算量較大。針對計算量優化，Fitz提出采用自相關的頻率估計方法，Jiang提出采用差分前項頻偏估計方法，但其性能在信噪比方面有惡化。與相關的技術方法相比，本文中頻率估計的優點在于與通信傳輸數據固有幀結構特點緊密結合，無其他額外要求，易于實現，復雜度低。可根據系統需求靈活設計導頻符號插入間隔和提取長度改變最終的頻率估計精度；兩步頻率估計采用的估計方法靈活，可采用計算簡單的矩形窗加快速傅里葉變換估計方法，結構和計算簡單，節省硬件資源；兩步頻率估計結果簡單整合即是最終的高精度頻率估計值。

1 信號模型

發送端進行連續組幀，在數據的不同位置插入2種不同的導頻信號，這2種導頻信號包括同步導引和導頻符號，其中，同步導引為集中導頻，導頻符號為分散導頻。發送端根據頻率估計范圍和精度的要求，在數據起始位置插入同步導引p(n)(n=0,1,…,N-1)，后等間隔M插入導頻符號q(n)(n=0,1,2,…)。設定同步導引長度N，導頻符號插入間隔M，傳輸的符號速率fsym，幀格結構如圖1所示。

圖1 信號幀結構Fig.1 Signal frame structure

插入的同步導引和導頻符號無特殊格式要求，同步導引與常規同步頭一致，導頻符號可為連續“1”或特定的偽隨機序列。插入的集中導頻和分散導頻用于FFT頻率估計和載波環路跟蹤。

頻率估計原理框圖如圖2所示，首先用集中導頻即同步導引數據做FFT，完成對大頻偏的粗估計，并將信號按頻偏值fΔ1進行搬移，使得搬移后的信號接近零頻；然后用分散導頻即導頻符號做FFT，完成小頻偏的精估計。最后將大頻偏估計值fΔ1和小頻偏估計值fΔ2相加，送入數字下變頻對接收信號進行頻率搬移，完成頻偏估計及校正。

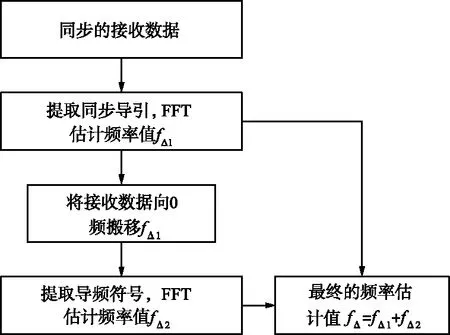
圖2 頻率估計原理框圖Fig.2 Functional block diagram of frequency estimation

2 頻率估計方法2.1 頻率估計分析

接收端在同步和位定時基礎上，對同步導引共軛相關得到恒模序列m(n)=p(n)p*(n)，此時采樣率fs1與傳輸的符號速率fsym相同，對m(n)進行N點FFT得M(k)，根據采樣率fs1和|M(k)|最大值所對應位置(可采用其他頻率估計方法)，計算頻率初步估計值fΔ1。

根據傳輸符號速率和同步導引長度計算第一步頻率估計最大值fmax1和粗估計精度fmin1，如下：

采用矩形窗加FFT估計法計算頻率值，過程如下：

以第一步估計的頻率值fΔ1在接收端產生本振信號，對后續接收數據r(n)進行差頻頻譜搬移得到r′(n)，過程如下：

式中，Re(·)表示取表達式實部；r*(n)表示r(n)的正交分量。

從搬移得到的信號中提取長度為L的導頻符號q′(n)，即將數據采樣率降低至fsym/M，頻率估計實現與第一步相同，首先將接收導頻符號與本地導頻符號的共軛q*(n)相乘，得到估計序列vL(n)，再進行FFT頻率估計，計算得到精確估計值fΔ2，該步頻率估計最大范圍和能夠達到的精度分別為fmax2和粗估計精度fmin2，計算如下：

為保證2步頻率估計之間的繼承性，第二步估計最大范圍fmax2與第一步粗估計精度fmin1需要滿足：

fmin1≤fmax2。

進一步推導得出導頻符號插入間隔M與同步導引長度N需要滿足：

完成不同采樣率數據的兩步頻率估計，得到相應的頻率估計值(頻率值存在正負之分)，將二者相加得到最終的高精度頻率估計值，即：

fΔ=fΔ1+fΔ2。

2.2 實現方式

同步導引長度N是通信系統根據應用場景和系統性能要求而定，導頻符號插入間隔M和接收端提取長度L是由頻率估計精度需求決定，M和L的乘積越大則頻率估計精度越高，同時L不變M越大，則計算復雜度越小。下面進一步對本方法的過程作詳細說明，其參數配置并不影響本方法的一般性。

設通信系統傳輸符號速率fsym=1 MB/s，同步導引為長度N=511的m序列，導頻符號插入間隔為M=128個符號，即2個導頻符號時間相距M/fsym=0.000 128 s。同步導引在同步幀起始位置，導頻符號是在同步幀和數據幀中均勻插入。

接收端通過同步導引相關峰檢測完成嚴格的時間和符號同步，進而實現以符號速率fsym的最佳采樣，得到接收數據r(n)，包含接收的同步導引、數據和導頻符號。

將接收的同步導引與接收端本地導引的共軛(由于插入的同步導引為m序列，其共軛即導引本身)相乘，得到輸入FFT頻率估計模塊的符號序列m(n)，由于m(n)長度N=511，為進行FFT運算，需要在末尾添加一個0。若傳輸信道產生的總頻偏為101 020 Hz，根據頻率估計流程圖3的方法，首先計算K值為26，則第一步估計的頻率為fΔ1=101 760 Hz。

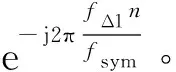
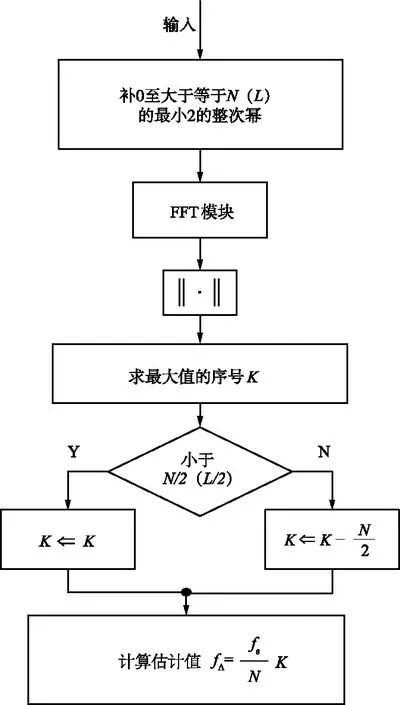
圖3 FFT頻率估計流程Fig.3 The flow chart of FFT frequency estimation

在實際實現中，FFT校頻處理要在搜幀同步并延時一定信息幀后開始啟動。在搜幀同步后延時是為了防止由于AGC未穩定時信號幅度不穩定造成FFT校頻錯誤。在速率較高時延時的信息幀數可以適當放寬(在速率為數Mb/s量級時由于速率高即使放寬十多幀，反映到時間上在毫秒量級)，在低速率時延遲的信息幀數量適當減少。可以有效地減少FFT校頻處理的時間開銷。

3 仿真

仿真模型采用BPSK調制，信號成形采用平方根升余弦脈沖，理想的符號定時同步無差分編碼和信道編碼。Es/N0=0 dB，速率1 Ms/s；數據輔助，多普勒頻率變化率為450 kHz/s。進行FFT頻率跟蹤。跟蹤后的剩余頻差如圖4所示，可以看出，剩余頻差小于符號率的2%，滿足后續載波恢復的入鎖條件。

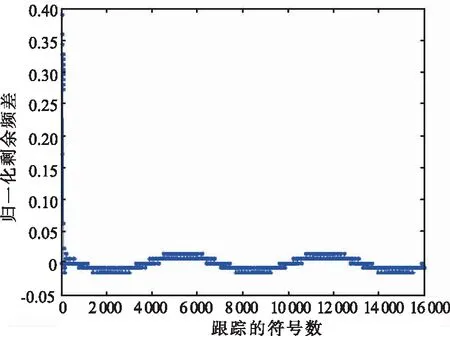
圖4 頻率跟蹤誤差Fig.4 Frequency tracking error

本地載波和原始載波的對比如圖5所示。

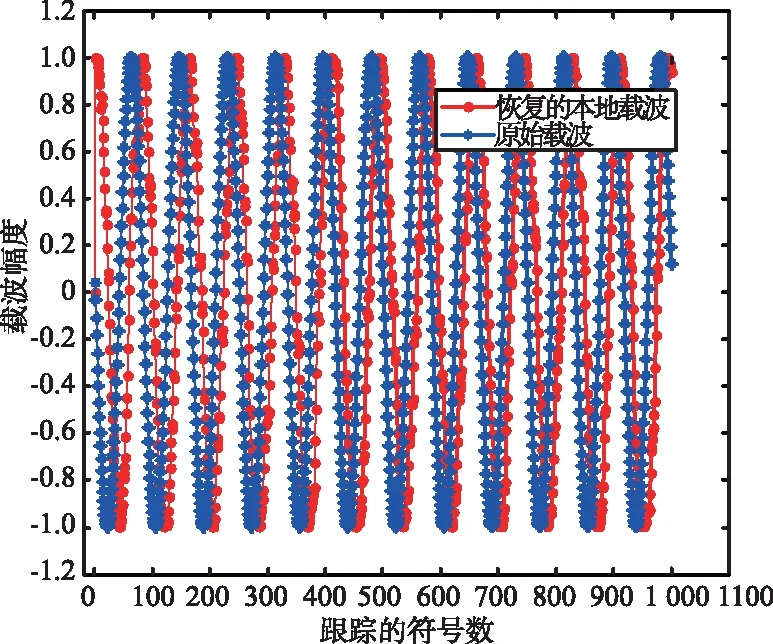
圖5 本地載波和原始載波的對比Fig.5 Comparison of local carrier and original carrier

載波同步包括載波頻偏的初始校正和后續的載波相位跟蹤。利用設計的幀結構中的冗余信息所進行的FFT頻率校正可以把初始頻偏校正至符號速率的1%之內，高精度的頻率估計有利于快速的載波環路同步和后續的載波相位跟蹤處理。

4 結束語

本文設計一種變采樣率的高精度頻率估計方法，包括依據估計精度需求進行同步導引長度和導頻符號間隔設計、基于FFT的頻率估計實現、結合頻率粗估計進行數據頻譜搬移、提取導頻符號進行頻率細估計、對2次估計結果整合得到最終頻率估計值。而且能夠根據需求，靈活設計導頻符號插入間隔和提取長度，同時滿足計算復雜度和估計精度的要求，通過兩步FFT計算實現高精度頻率估計，有效解決通信中的高動態頻偏矯正問題。經仿真驗證，在通信系統同步基礎上，本文方法能夠實現逼近克拉美羅限的估計精度，滿足后續載波相位跟蹤的要求。