一種GNSS-R鏡面反射點精確估計方法

俞永慶，杜 毅

(1.中國石油化工股份有限公司 勝利油田分公司，山東 東營 257000；2.北京航空航天大學 電子信息工程學院，北京 100191)

0 引言

全球導航衛星系統反射信號(Global Navigation Satellite System Reflectometry,GNSS-R)技術是一種新型遙感技術，以導航衛星信號作為信號源，通過處理目標物反射信號獲得反射面物理參數[1]。與傳統遙感技術相比，GNSS-R具有高時空分辨率、寬刈幅、低功耗和應用領域廣泛等優勢[2]，成為近些年的研究熱點。

鏡面反射點是反射區的中心，是確定反射區位置的參考點[3]，精確估算鏡面反射點對反演目標以及碼相位偏移[4]的確定具有重要意義。迄今為止，鏡面反射點估計方法主要有S.C.Wu算法[5]、Gleason算法[6]和線段二分法[7]。其中線段二分法利用二分查找原理對S.C.Wu算法進行改進，獲得較高的收斂速度，可快速估算鏡面反射點。但是，線段二分法采用地球橢球模型，使鏡面反射點收斂到基準橢球面之上。基準橢球面與實際地表之間存在較大偏差，特別是隨著土壤濕度[8]、植被覆蓋[9]等陸面GNSS-R應用的發展，反射點處的海拔高度已成為鏡面反射點估計時不可忽視的誤差源。針對上述問題，在線段二分法的基礎上引入Google Elevation API提供的海拔信息作為修正量，使鏡面反射點最終收斂到實際地形之上，提高鏡面反射點的估計精度。

1 GNSS-R幾何關系

GNSS-R幾何關系如圖1所示，其中O為地心，R為接收機位置，T為GNSS衛星位置，S為鏡面反射點位置，M為OS延長線與線段RT的交點，αr為向量SR與向量SM之間的夾角，αt為向量ST與向量SM之間的夾角。由幾何光學理論可知，S為鏡面反射點的充要條件是αr=αt。

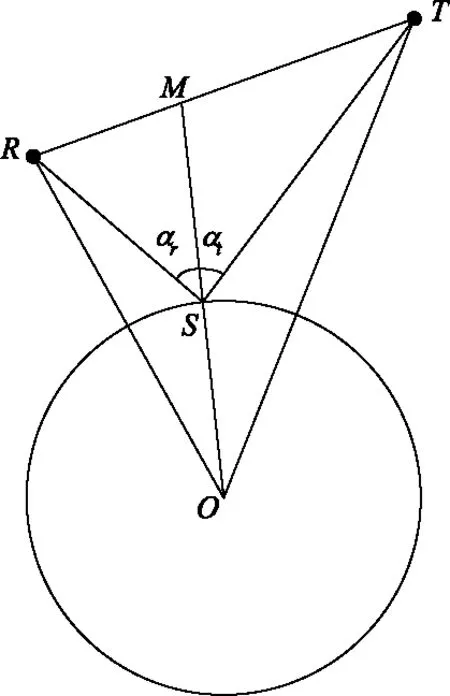
圖1 GNSS-R幾何關系Fig.1 GNSS-R geometric relationship

2 傳統鏡面反射點估計方法誤差分析

大地水準面、基準橢球面和實際地面三者之間的關系如圖2所示。

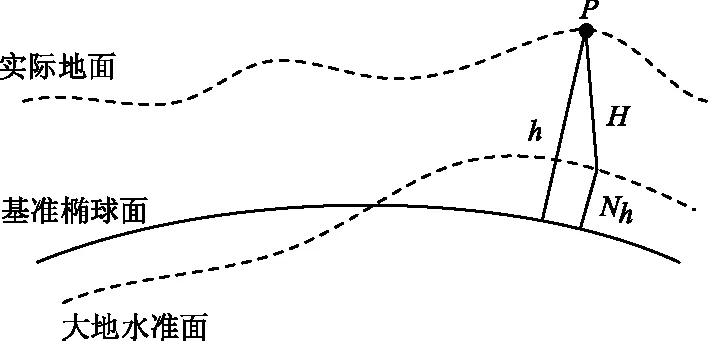
圖2 海拔誤差示意Fig.2 Schematic diagram of elevation error

P為實際地面上一點，其大地高度h是該點到基準橢球面的法線距離，其海拔高度H是該點到大地水準面的法線距離，大地高度h與海拔高度H存在如下近似關系[10]：

h≈H+Nh，

(1)

式中，Nh是大地水準面高度，即大地水準面高出基準橢球面的法線距離，由于基準橢球面是一個最接近于大地水準面的橢球面，因此P點的大地高度值可以近似視為海拔高度值，即：

h≈H。

(2)

在本文后續分析中，認為大地高度h與海拔高度H相等。由Kirchhoff幾何光學模型[11-13]可知，收斂到實際地表的鏡面反射點pe與收斂到基準橢球面上的鏡面反射點po水平方向偏差Δd滿足如下關系：

(3)

式中，a，b為常數，由衛星、接收機和鏡面反射點三者所構成的幾何關系決定；h為鏡面反射點處的海拔高度。由式(3)可知，傳統鏡面反射點估計算法的估計誤差與反射點處的海拔高度呈正相關。

3 修正海拔誤差的鏡面反射點估計算法

3.1 Google Elevation API

本文在基于線段二分法的鏡面反射點估計算法基礎上引入Google Elevation API提供的海拔高度進行誤差修正，使鏡面反射點最終收斂到實際地表。Elevation API可以提供地表任意一點的海拔數據，該接口的使用方式如圖3所示，用戶只需要輸入目標點的緯度以及經度，便可以得到該點的海拔高度。

圖3 Google Elevation API使用方式Fig.3 Application of Google Elevation API

3.2 基于線段二分法的鏡面反射點估計算法

基于線段二分法的鏡面反射點估計算法利用折半查找原理減少迭代次數，其具體工作流程如圖4所示。首先，初始化搜索區間兩端點a=R、b=T，計算ab中點M，并通過M點坐標得到其星下點S；然后，分別計算向量SR與向量SM之間的夾角αr以及向量ST與向量SM之間的夾角αt；最后，判斷αr與αt的大小關系，若αr=αt則退出迭代并輸出S點坐標；若αr<αt則令搜索區間端點b=M并進行下一輪計算；若αr>αt則令搜索區間端點a=M并進行下一輪計算。

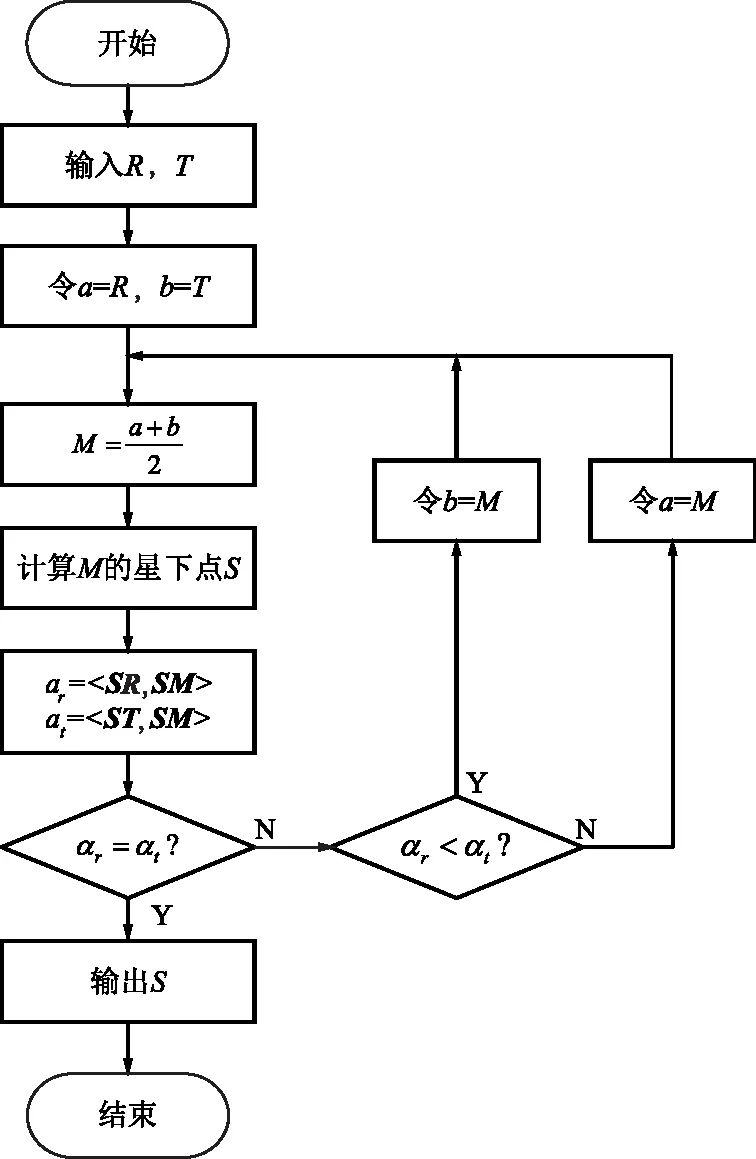
圖4 線段二分法工作流程Fig.4 Work flow of dichotomy of line segment

3.3 修正海拔誤差的鏡面反射點二分查找估計算法

訪問Google Elevation API存在大約100 ms的時延，在迭代過程中頻繁地調用API會嚴重影響計算速度。為了盡量減少API的調用次數，本文將鏡面反射點估計方法分為預估計和誤差修正2個階段。其中預估計階段與上述基于線段二分法的鏡面反射點估計算法完全一致，該階段輸出收斂到基準橢球面上的鏡面反射點坐標。誤差修正階段的工作流程如圖5所示，首先獲取預估計階段輸出鏡面反射點S的緯度以及經度，訪問API獲取S點處的海拔高度h。然后判斷h是否為零，若是則直接輸出S；否則，重新進行二分查找，在確定S點坐標時將其大地高度設置為h。

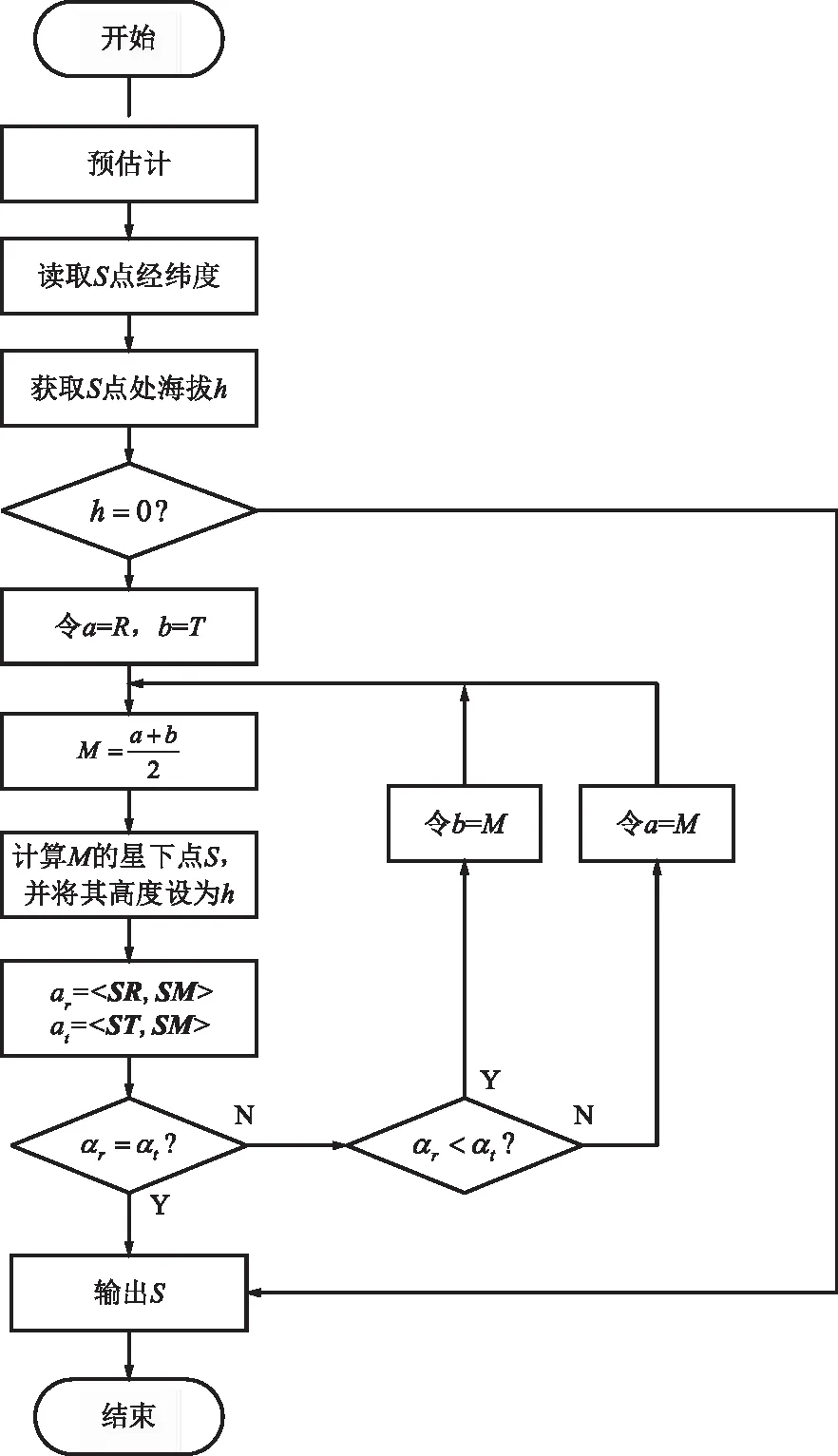
圖5 誤差修正階段的工作流程Fig.5 Work flow of error correction stage

4 反射事件時空分布統計

為了分析引入海拔誤差修正對鏡面反射點估計精度的影響，本文對傳統線段二分法和引入海拔誤差修正后的線段二分法進行對比分析。

4.1 固定探測目標

首先分析反射面海拔固定，改變接收機和GNSS衛星位置時的鏡面反射點估算精度。反演目標設置為中國最大的內陸湖泊——青海湖，其湖面海拔約3 194 m。接收機為軌道高度695 km的LEO衛星，GNSS衛星為軌道高度21 528 km的北斗MEO衛星。選取不同的接收機和GNSS衛星位置組合，共得到5組仿真數據，具體坐標設置如表1所示。

表1 接收機及GNSS衛星位置Tab.1 Positions of receiver and GNSS satellite

分別使用未進行海拔誤差修正的線段二分法和引入海拔誤差修正的線段二分法估算鏡面反射點，具體結果如表2所示。

表2 2種方法估計的鏡面反射點坐標Tab.2 Coordinates of specular points estimated by two methods

可以看出，二者在水平方向以及豎直方向上均存在一定的偏差，其中豎直方向偏差為鏡面反射點處的海拔高度。

為了進一步分析接收機和衛星位置對鏡面反射點估計偏差的影響，計算引入海拔誤差修正線段二分法得到的鏡面反射點處的衛星高度角，并計算相同條件下2種方法輸出鏡面反射點之間的水平方向偏差和豎直方向偏差，結果如圖6所示。由圖可知，水平方向偏差與高度角呈一次函數關系，通過最小二乘擬合將數據點擬合為直線，得到水平方向偏差隨高度角增加的變化率為-49.02，而豎直方向偏差與鏡面反射點處的海拔高度有關，與衛星及接收機位置無關。

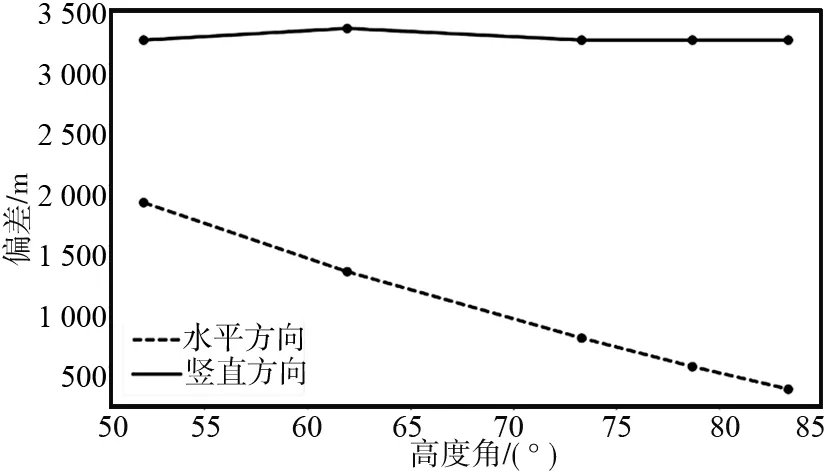
圖6 誤差與衛星高度角關系Fig.6 Relationship between error and elevation of satellite

4.2 固定接收機與GNSS衛星之間的相對位置

為了分析海拔變化對鏡面反射點估算精度的影響，假設接收機運行在北緯39°線上空，軌道高度為695 km，GNSS衛星運行在北緯30°線上空，軌道高度為21 528 km，且始終保持二者位于同一經度。令接收機和GNSS衛星繞地球運行一周，以5°為步進估算鏡面反射點。計算得到鏡面反射點處海拔高度、2種算法輸出的鏡面反射點之間水平方向偏差以及豎直方向偏差，其對應關系如圖7所示。由圖可知，鏡面反射點估算精度的提升幅度與反射點處海拔高度呈正相關。

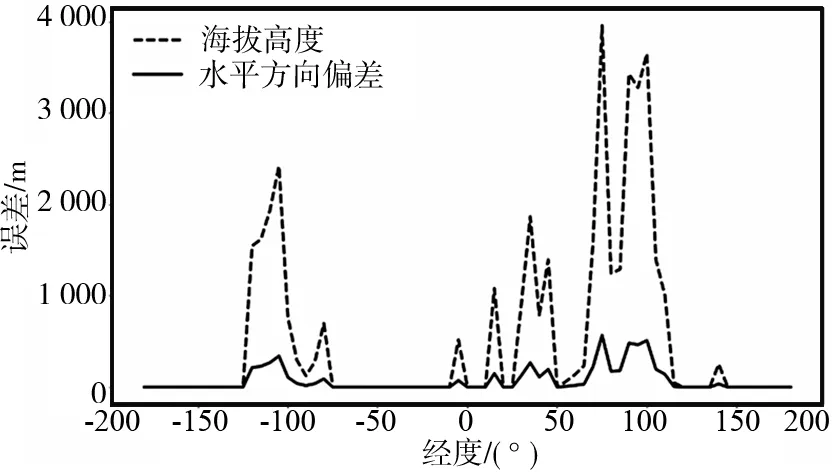
圖7 反射點處海拔高度和水平誤差與經度的關系Fig.7 Relationship between elevation of specular point and horizontal error with longitude

5 結束語

在傳統線段二分法的基礎上引入Google Elevation API提供的海拔信息對鏡面反射點進行修正，提出了一種精確的鏡面反射點估計方法。通過對比實驗驗證了該方法可消除海拔偏差，獲得更高精度的鏡面反射點。該方法繼承了線段二分法迭代次數少、運算時間短的優點，將鏡面反射點收斂到真實地表，使得鏡面反射點估算精度得到提升。但是，該方法依賴于Google Elevation API所提供數據的準確性和穩定性，并且訪問該接口有約100 ms的時延，導致整體處理速度較慢，未來可通過建立離線數據庫的方式改善接口調用延遲。