不平衡電網(wǎng)下儲能系統(tǒng)直流紋波分析及抑制策略

余萬榮，丁宇潔，李歡，肖小兵，田浩，蔣澤甫

（1.貴州電網(wǎng)有限責任公司安順供電局，貴州安順561000；2.清華大學電力系統(tǒng)及發(fā)電設備控制和仿真國家重點實驗室，北京100084；3.清華大學電機系北京100084；4.貴州電網(wǎng)有限責任公司電網(wǎng)規(guī)劃研究中心，貴州 貴陽550003）

近年來，隨著資源、環(huán)境問題日益嚴峻以及人們環(huán)保意識的增強，基于電力電子變流技術的光伏（photovoltaic，PV）、風電（wind generation，WG）等可再生能源（renewable energy sources，RES）得到了迅速發(fā)展，其裝機總?cè)萘坎粩嗌仙齕1-2]。同時，由上述單元構成的微電網(wǎng)逐漸得到推廣、應用。為降低可再生能源發(fā)電間歇性、不確定性等對微電網(wǎng)穩(wěn)定性造成的不利影響[3-4]，通常在微電網(wǎng)中配備一定容量的儲能裝置。根據(jù)不同應用環(huán)境和應用等級，目前工程中儲能主要為采用兩電平變流技術的電池儲能系統(tǒng)，但基于多電平技術的儲能系統(tǒng)正逐漸受到廣泛關注和研究[5-7]。

由于微電網(wǎng)容量等級相對較小，因此單相負載或不平衡負載很容易引起微電網(wǎng)的不平衡運行。電網(wǎng)的不平衡嚴重影響到了微網(wǎng)中變流器的安全可靠運行以及電能質(zhì)量等[8]。此外，不平衡的負載將在變流器直流母線電流中引入低頻紋波分量[9]，而文獻[10]指出低頻紋波電流將會增大燃料電池的瞬時輸出功率，這將使燃料電池容量增大，成本增加。且當二次紋波電流超過額定電流的8%時，電池效率下降，使用壽命縮短。

針對上述問題，文獻[9]通過控制方法利用LCL濾波器中的電容提供不平衡負載引入的二次脈動功率，但該方法需要較大通流能力的濾波電容。文獻[11]采用兩級拓撲方式，通過控制前級變換器抑制低頻脈動分量進入電池側(cè)，但該方法不能完全消除進入電池的低頻電流，且流經(jīng)前級變流器的功率較大，系統(tǒng)效率降低。

根據(jù)電力系統(tǒng)中“電力彈簧”的概念[12]，本文在此基礎上提出了直流母線并聯(lián)Buck-Boost型直流電力彈簧（DC electrical spring，DCES）的有源低頻電流紋波抑制方法。首先，通過建立三相兩電平變流器的開關函數(shù)模型，分析了不平衡負荷下，直流母線低頻紋波電流的產(chǎn)生機理，并給出了電流的時域表達式。隨后，建立了DCES的頻域模型，給出了采用改進型復合控制的低頻紋波電流抑制方法，并利用小增益理論對該控制策略的穩(wěn)定性進行了分析。最后，利用仿真模型和實驗樣機對DCES以及所提控制策略的可行性進行了驗證。

1 低頻紋波電流分析

為簡化不平衡負荷條件下直流側(cè)低頻紋波電流產(chǎn)生機理的分析，本文以如圖1所示的三相兩電平儲能逆變器為例進行討論，且逆變器采用正弦脈沖寬度調(diào)制（sinusoidal pulse width modulation，SPWM）。同時假設圖1中交流測三相電流ia，ib，ic均為工頻正弦波。id表示直流母線電流；Q1～Q6分別表示三相橋臂中的功率器件。

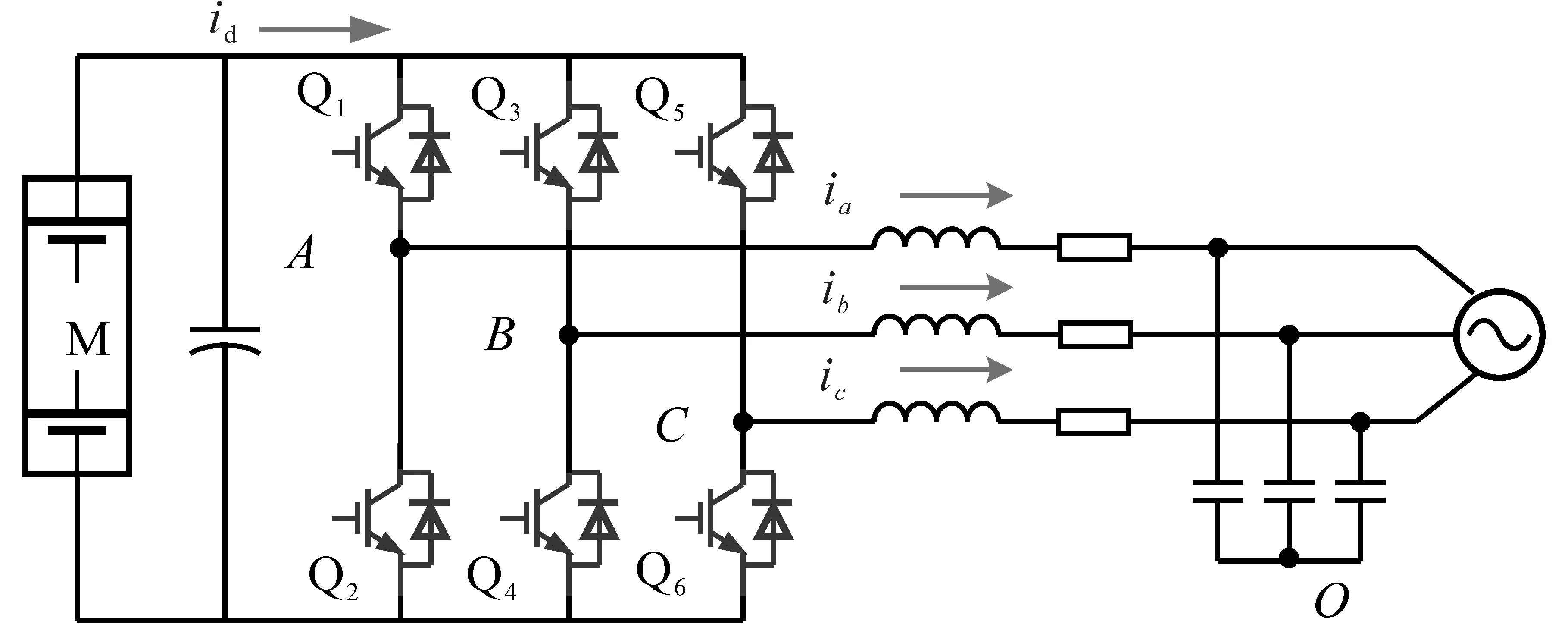
圖1 三相儲能逆變器并網(wǎng)結(jié)構圖Fig.1 Structure of grid-tied three-phase inverter

假設Sa，Sb，Sc分別為對應各相的橋臂的開關函數(shù)，且規(guī)定橋臂上與正母線相連的功率器件導通時Sj=1，j=a，b，c；與負母線相連的功率器件導通時Sj=-1。

采用開關函數(shù)的傅立葉形式構成SPWM調(diào)制逆變器的開關門信號，用以描述逆變器的電流和電壓，并通過分析得出逆變器直流側(cè)輸入電流的諧波分量。電壓型逆變器開關函數(shù)的傅里葉表達式為

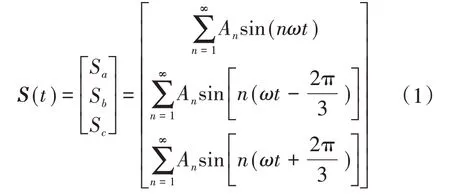
式中：ω為逆變器輸出電壓的基波角頻率；An為輸出電壓n次諧波的幅值系數(shù)，n=1，3，5，7，…。

開關函數(shù)描述的逆變器直流側(cè)電流的表達式為

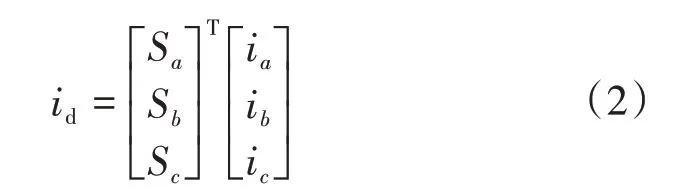
整理得

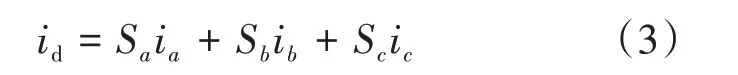
當圖1所示逆變器接入的電網(wǎng)存在三相不平衡負荷時，不考慮開關器件死區(qū)時間的影響，此時三相電流表達式為

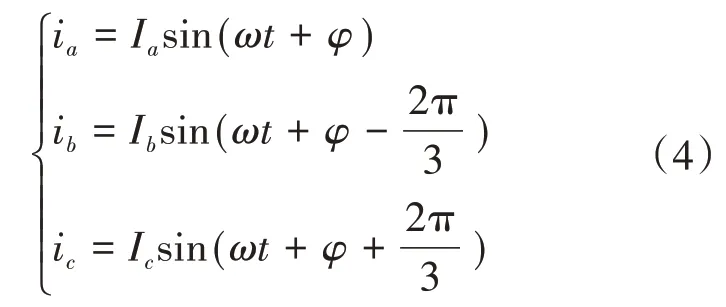
式中：φ為輸出電流相位角；Ia，Ib，Ic分別為各相電流的幅值。

對于圖1所示三相三線制逆變器，電流零序分量為0，即

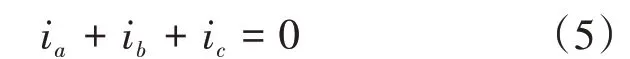
利用對稱分量法對式（4）進行處理，可得不平衡相電流中正、負序分析分別為

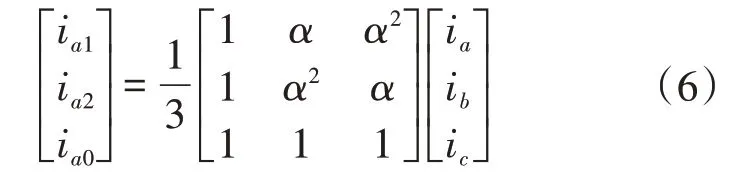
其中 α=ej120°

式中：ia1，ia2，ia0分別為正序、負序和零序電流分量。

將式（4）和式（5）代入式（6），整理得電流各序分量表達式分別為

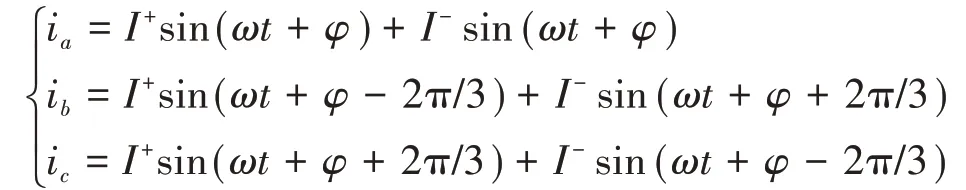
其中

式中：I+為逆變器輸出電流的正序分量幅值；I-為負序電流分量幅值；γ為輸出三相電流的不平衡度。

結(jié)合式（1）、式（3）和式（7），可得不平衡負荷情況下逆變器直流側(cè)電流時域表達式如下式：

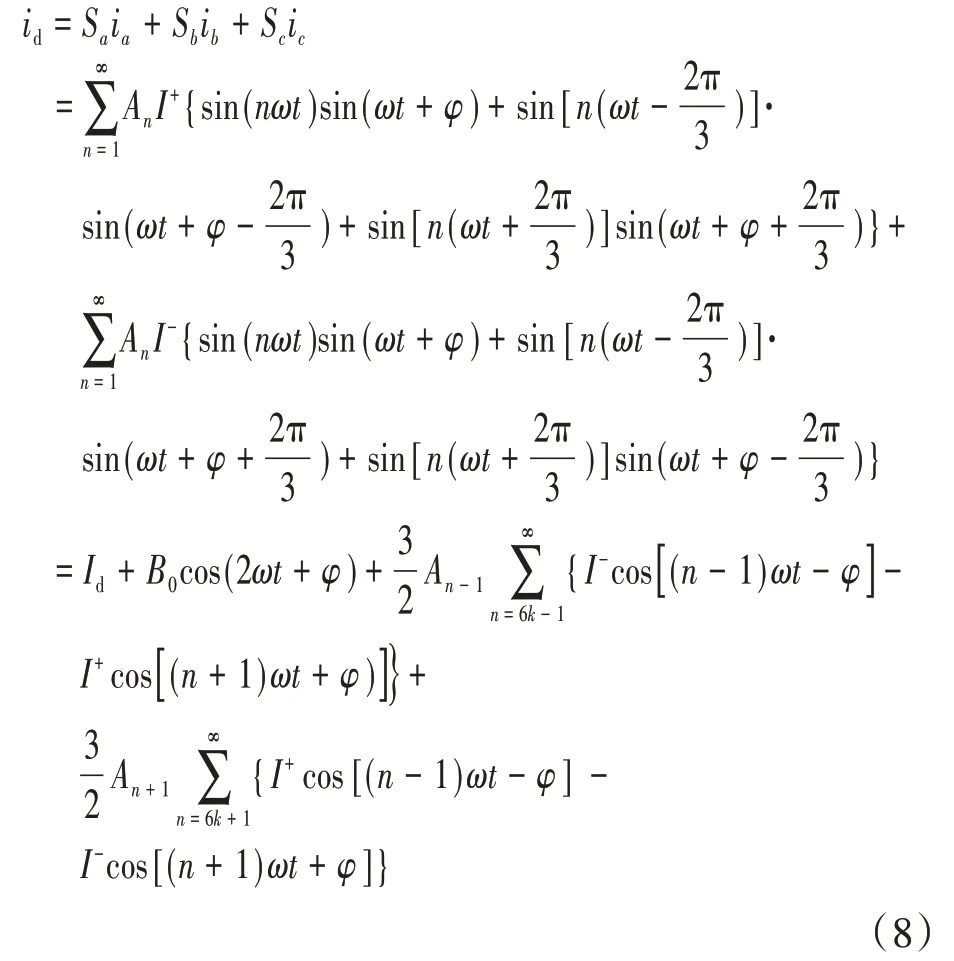
其中

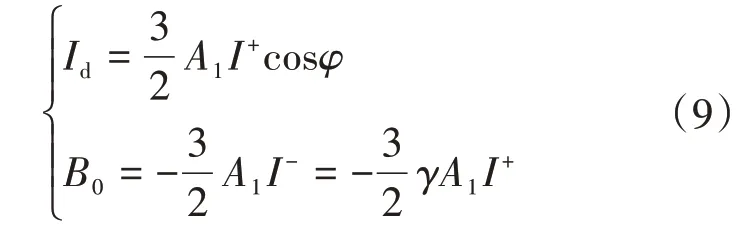
根據(jù)式（8）和式（9），可以看出，在忽略功率器件死區(qū)時間情況下，帶不平衡負荷運行時，三相逆變器的直流側(cè)電流主要包含直流分量、二次紋波分量以及其他高次諧波。其中二次電流紋波由三相不平衡負荷產(chǎn)生的負序電流引入，且其幅值與三相負荷的不平衡度γ成正比，即微網(wǎng)中負荷的不平衡度愈嚴重，逆變器直流母線上的二次電流紋波越大。文獻[10]指出，過大的低頻電流脈動將加劇儲能系統(tǒng)電池的熱老化，降低使用壽命。

此外，由于占主要成分的電流分量頻率較低，傳統(tǒng)的通過直流母線支撐電容吸收電流紋波的方法難以達到滿意效果，且大容量的電容將進一步提高系統(tǒng)成本并增加體積。針對上述問題，本文提出采用基于Buck-Boost拓撲結(jié)構的DCES對低頻電流分量進行有源抑制。

2 Buck-Boost型DCES及控制策略

圖2給出了集成DCES后的儲能變流器拓撲結(jié)構。其中，電感L、電容C以及功率器件Q7和Q8組成DCES。相比于圖1中直接在直流側(cè)并聯(lián)電容的方法，本文所提有源抑制方法能更為有效地吸收電流低頻紋波分量。

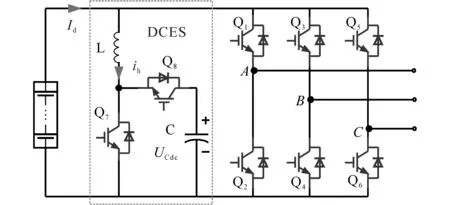
圖2 集成DCES的逆變器拓撲Fig.2 Topology of inverter integrated with DCES

2.1 DCES頻域模型

根據(jù)圖2可以看出，DCES的拓撲結(jié)構為Buck-Boost型，分析其工作原理可知，在1個二倍工頻周期內(nèi)，其先后工作與Boost模式和Buck模式。為建立DCES的頻域模型，根據(jù)上述工作模式，分別進行討論。當DCES工作在Buck模式時，其拓撲結(jié)構等效為圖3所示。其中，電阻R為電容C的等效并聯(lián)電阻。

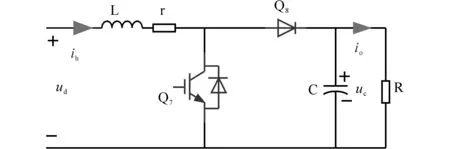
圖3 Boost工作模式下等效電路結(jié)構Fig.3 Equivalent topology of DCES under Boost mode

根據(jù)圖3，可得電容電壓uc和電感電流ih的時域模型表達式為

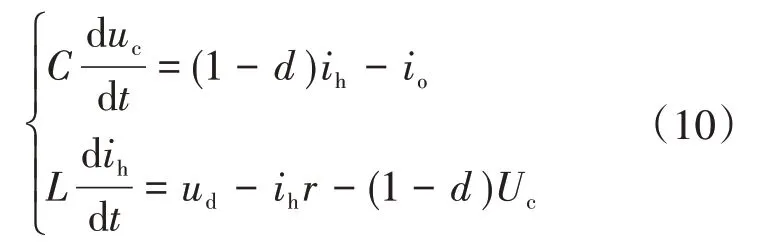
式中：ud為直流母線電壓；Uc為電容穩(wěn)態(tài)電壓；r為電感寄生電阻；d為某一時刻時的工作占空比。

對電壓、電流添加小擾動后可得

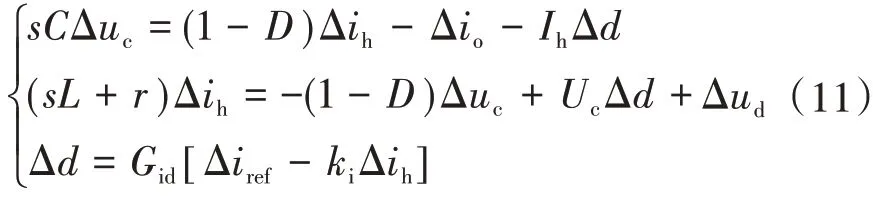
式中：ki為電流采樣增益；Gid為控制系統(tǒng)的指令增益，本文中即為復合控制傳遞函數(shù)；Δiref為電流參考量；Ih為穩(wěn)態(tài)電感電流。

考慮直流母線電壓和電容電壓波動比例很小，令Δud=0，Δuc=0，則

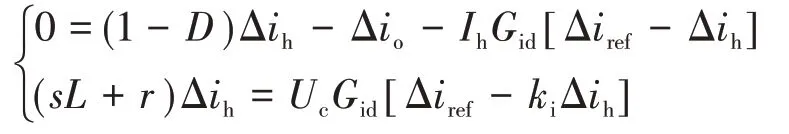
結(jié)合式（11）和式（12），可得DCES工作在Boost模式時的電流閉環(huán)控制框圖，如圖4所示，其中，G1為DCES頻域模型。

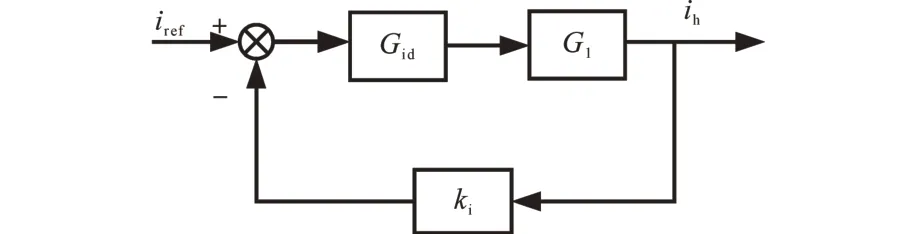
圖4 Boost工作模式下控制框圖Fig.4 Control block of DCES under Boost mode

同理，根據(jù)工作原理可推導出DCES工作在Buck模式下的頻域模型及控制框圖，其與圖4所示一致。受篇幅限制，本文中不再逐一推導。

2.2 DCES復合控制

根據(jù)DCES工作原理可知，電流ih為交流量，傳統(tǒng)的PI控制器難以實現(xiàn)無靜態(tài)誤差跟蹤，而多PR控制器并聯(lián)的方法較為復雜、計算量大。為此本文提出采用PI控制+重復控制（repetitive control，RP）的復合控制DCES方法。重復控制為基于內(nèi)模原理的一種控制方法，通過對其內(nèi)模參數(shù)的設置，可實現(xiàn)對某一頻率及其倍數(shù)頻率的交流量的無靜差跟蹤，其離散域內(nèi)的控制框圖如圖5所示。

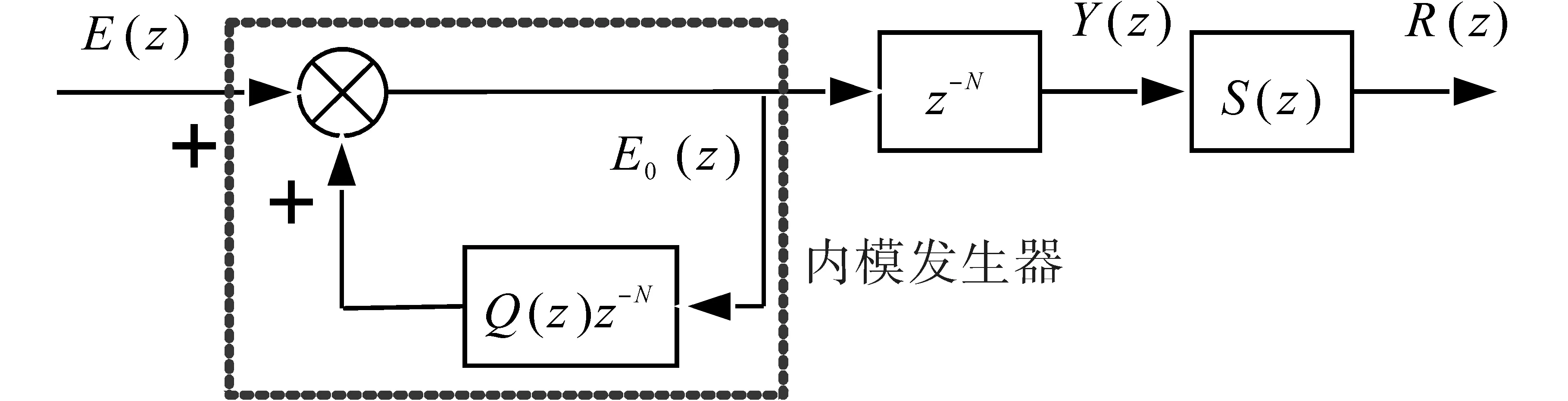
圖5 離散域下重復控制原理框圖Fig.5 Control block of repetitive control in z-domain

圖5中，E（z）為重復控制器的輸入誤差的離散量；S（z）為控制器補償函數(shù)，通常設置為二階低通濾波傳遞函數(shù)；Q（z）為提高系統(tǒng)穩(wěn)定性和魯棒性的內(nèi)模衰減函數(shù)，其通常取值為小于1的常數(shù)或一階低通濾波傳遞函數(shù)；Y（z）為輸出離散量。根據(jù)圖5，可得出離散域下重復控制的內(nèi)模傳遞函數(shù)為

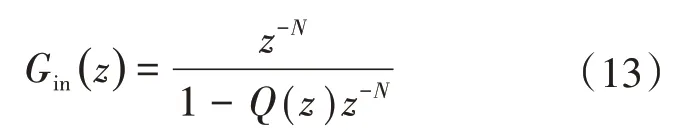
式中：N為一個紋波電流脈動周期內(nèi)的采樣點數(shù)。

參考文獻[13]，本文中選取Q（z）=0.95。

根據(jù)式（13），分別給出重復控制和準PR控制Bode圖，如圖6所示。由圖6可以看出，與準比例諧振控制方式比較，重復控制在基波及其周期頻率出均存在諧振峰值，表明其對周期次環(huán)流諧波的均具有良好的抑制效果。此外由于重復控制和準比例諧振控制對直流偏置分量的抑制效果較差，因此，為保證DCES的穩(wěn)定運行，本文提出采用PI控制+重復控制的復合控制策略。傳統(tǒng)的復合控制為上述兩種控制方式的簡單并聯(lián)，雖然便于參數(shù)整定，但重復控制器的補償函數(shù)設計困難。

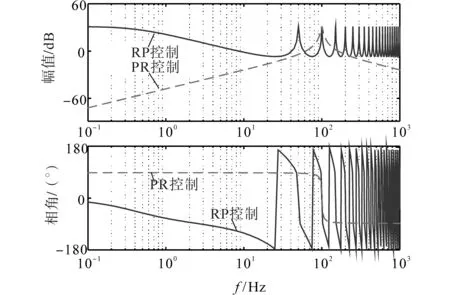
圖6 準比例諧振和重復控制Bode圖對比Fig.6 Comparison of quasi-PR control and RP control

對此，本文采用嵌入式結(jié)構的復合控制方式，根據(jù)2.1小節(jié)對DCES頻域模型的分析，令ki=1，做出DCES整體控制框圖結(jié)構，如圖7所示，其中PIv（z）為穩(wěn)壓PI控制器的離散域傳遞函數(shù)。

如圖7a所示，DCES的指令電流由兩部分構成，其一為保證DCES電容電壓穩(wěn)定的穩(wěn)壓控制環(huán)路，另一部分為變流器直流母線電流中提取得到的低頻紋波電流分量，為簡化控制過程，本文采用帶通濾波環(huán)節(jié)進行提取。

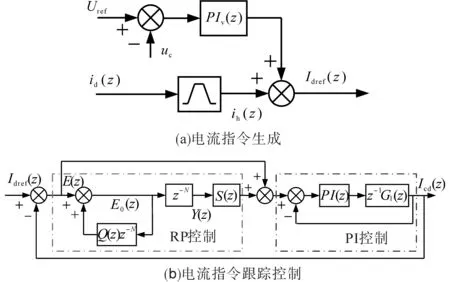
圖7 DCES控制框圖Fig.7 Control block of DCES

3 穩(wěn)定性分析及控制參數(shù)設計

根據(jù)圖7（b）所示電流環(huán)路控制框圖，可以看出，在控制過程中，指令誤差及重復控制輸出之和共同作為PI控制器的輸入。由于在暫態(tài)過程中，重復控制器需要1個周期的延時，此時控制系統(tǒng)的穩(wěn)定性由經(jīng)過前饋支路的PI控制部分決定。因此，可根據(jù)傳統(tǒng)控制設計方法，對內(nèi)環(huán)PI控制的參數(shù)進行設計。由PI控制特性可知，雖然此時PI控制無法達到無靜差的調(diào)節(jié)目的，但1個周期后，重復控制發(fā)揮作用并放大控制誤差，參與PI控制，當進入穩(wěn)態(tài)后，輸出電流即可實現(xiàn)對指令電流的無靜差跟蹤。根據(jù)圖7b可得出輸出與指令之間的離散域傳遞函數(shù)為

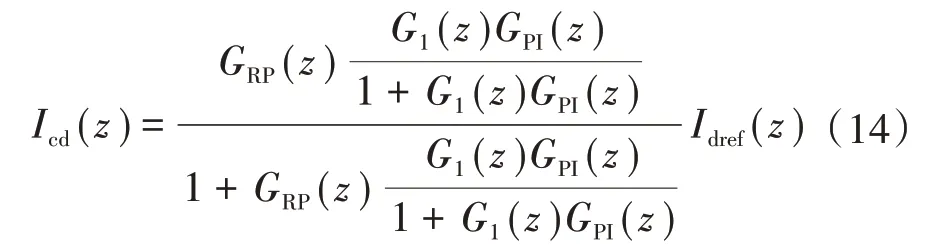
其中，GRP（z）為重復控制傳遞函數(shù)，其表達式為

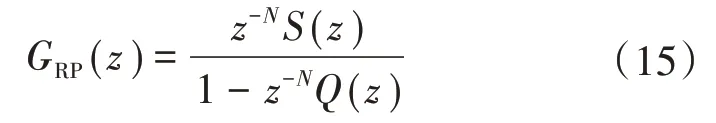
根據(jù)離散控制理論的小增益原理，為使系統(tǒng)處于穩(wěn)定狀態(tài)，離散系統(tǒng)的閉環(huán)傳遞函數(shù)的極點必須均位于單位內(nèi)。式（14）所示傳遞函數(shù)的特征方程為

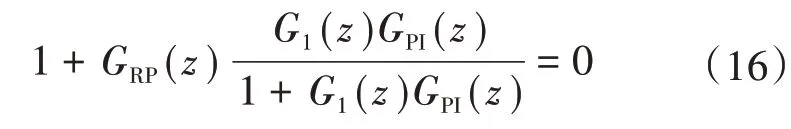
將式（15）代入式（16），整理后可得控制系統(tǒng)穩(wěn)定的條件為

在不同系統(tǒng)穩(wěn)定函數(shù)Q（z）情況下，根據(jù)式（17）可畫出添加補償函數(shù)S（z）前后系統(tǒng)穩(wěn)定條件不等式的復平面關系，如圖8所示，其中，ω∈[0,π/Ts]。

圖8 復合控制的穩(wěn)定性分析矢量圖Fig.8 Vector diagram for stability analysis of hybrid control

由圖8可以看出，當角頻率ω從零增大到奈奎斯特頻率時，所有特征根均被限制在一個單位圓內(nèi)，系統(tǒng)漸進穩(wěn)定。根據(jù)式（14）所示閉環(huán)傳遞函數(shù)特性，在高頻段時，系統(tǒng)相位存在較大滯后，補償器和控制對象在高頻段的大幅度幅值衰減導致S（eωTs）T（eωTs）的模很小，其軌跡也可能會進入第二、第三象限內(nèi)。對比取不同Q（z）時可行域與坐標軸的關系可以看出，在衰減函數(shù)取值小于1時，在系統(tǒng)小增益處的穩(wěn)定性更好。但圖7b所示控制框圖表明，較小的衰減函數(shù)將降低系統(tǒng)的增益，控制穩(wěn)態(tài)精度較差，綜合考慮本文中取Q（z）=0.95。

此外，根據(jù)式（17）及圖8可以看出，重復控制器的補償函數(shù)S（z）對控制系統(tǒng)穩(wěn)定裕度影響較大[14]。本文給定補償函數(shù)形式為

kc為重復控制前向通道增益，調(diào)節(jié)重復控制作用的強度，同衰減函數(shù)相似。

kc其取值較小時，穩(wěn)態(tài)誤差變大，但穩(wěn)定性得到提高。因此kc需要在穩(wěn)態(tài)誤差和穩(wěn)定性能之間折中考慮。

G2（z）對高頻段的幅頻特性進行矯正，主要作用為抑制高頻處的干擾，為提高G2（z）衰減能力，通常設其為二階低通濾波器，考慮補償帶寬，其截止頻率應略大于待補償環(huán)流諧波頻率。考慮其高頻衰減作用，本文中設定截止頻率為fn=1.35 kHz，阻尼系數(shù)為ξ=0.55。離散化后表達式為

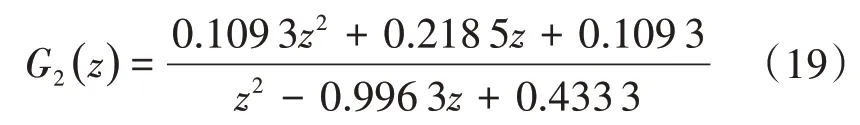
超前環(huán)節(jié)zk用來對PI控制器在中低頻段的滯后相位進行矯正。圖9給出了取不同k值時，補償后zkG2（z）T（z）的頻域特性，綜合考慮后本文中令k=4。

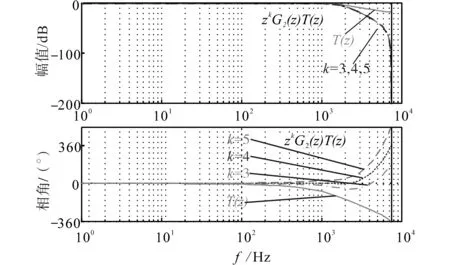
圖9 補償前后頻域特性對比Fig.9 Comparison of f-domain bode diagram between with and without compensation

4 仿真及實驗驗證

為驗證不平衡負荷下直流母線電流的頻域分布以及本文所提出的有源抑制策略及其控制設計的有效性，利用Matlab/Simulink搭建了380 V儲能變流器的仿真模型，其具體參數(shù)為：電網(wǎng)電壓Un=380 V，電網(wǎng)頻率fn=50 Hz，DCES開關頻率fs=10 kHz，DCES橋臂電感L=1.5 mH，DCES電容C=2.5 mF，比例系數(shù)kp=3.6，積分系數(shù)ki=18.8。

首先，對不平衡負荷下，儲能變流器的工作狀態(tài)進行仿真，設定三相純阻性負荷功率分別為5 kW，7 kW和6 kW。仿真結(jié)果如圖10所示。

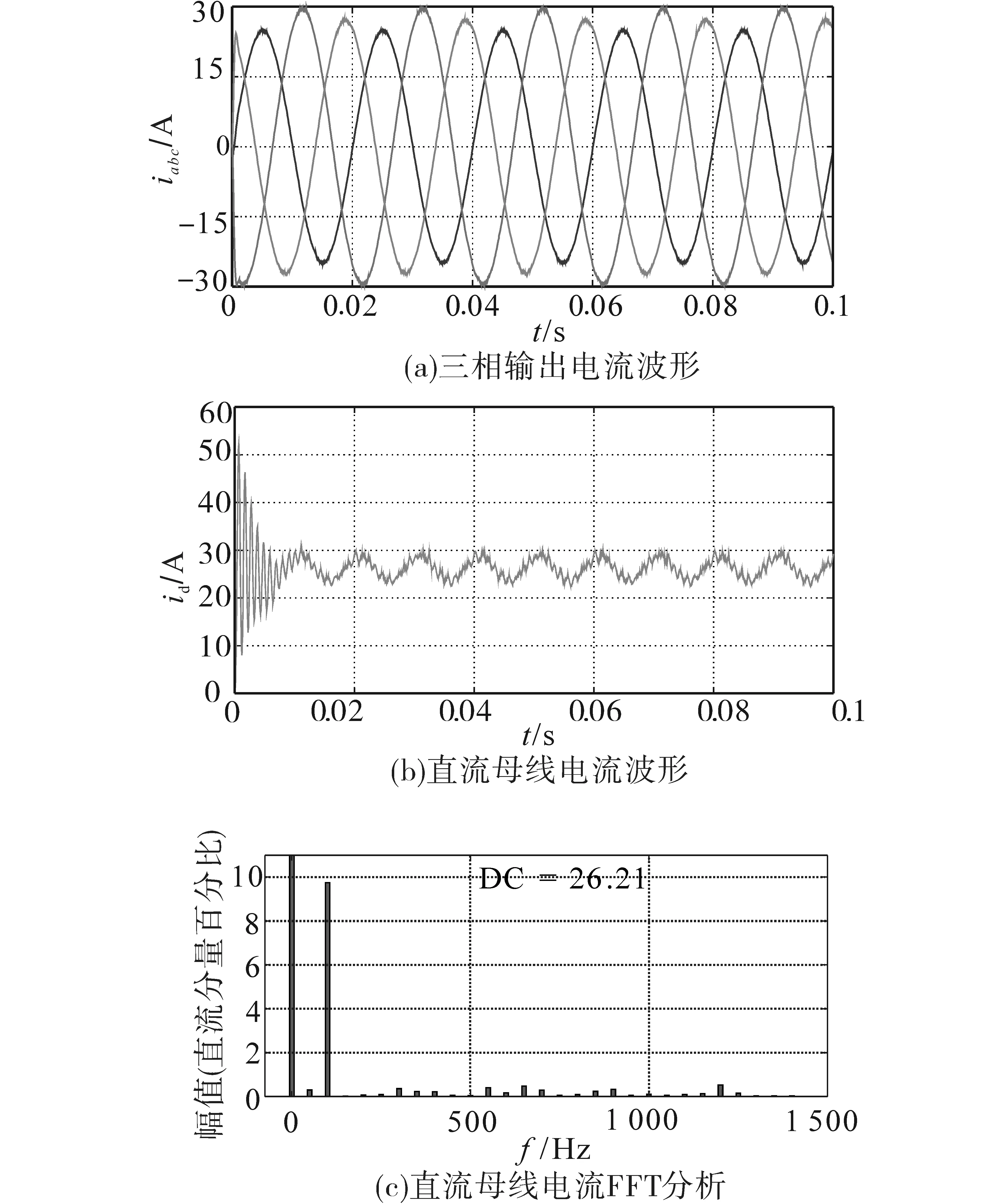
圖10 不平衡負荷下仿真波形Fig.10 Simulation waveforms under unbalance three-phase load

從圖10a可以看出，此時三相輸出電流處于不平衡狀態(tài)，而圖10b顯示直流母線電流存在脈動分量。對直流母線電流進行FFT分析，結(jié)果如圖10c所示。可以看出，此時直流母線電流中除直流分量外還存在較大分量的兩倍基波頻率的電流紋波。在不加抑制措施情況下，此低頻電流將直接進入電池內(nèi)，造成儲能電池過熱。

為驗證本文所提DCES的作用，在相同負載情況下，啟動DCES進行仿真，并對輸出相電流進行FFT分析，可得此時進入到電池的母線電流的頻域分布如圖11所示。

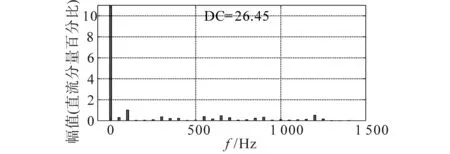
圖11 DCES工作時直流母線電流FFT分析Fig.11 FFT analysis of DC current with DCES

對比圖10c和圖11可以看出，在DCES作用后，進入儲能電池的電流中低頻紋波電流分量由開始的9.7%下降至0.86%。仿真結(jié)果對比驗證了DCES對直流母線低頻紋波電流抑制的有效性。

在仿真模型的基礎上，搭建了直流母線電壓為120 V，線電壓有效值為60 V，容量為2 kV·A的儲能實驗樣機。其中，采用TMS320F28335作為主控制器，功率器件為英飛凌的MOSFETSTW56N65M2-4，通過三相逆變器輸出連接不同阻值的電阻模擬不平衡負載。儲能變流器及DCES的開關頻率均為10 kHz。

上電后，在程序運行前期，DCES未投入使用，在某一時刻通過按鍵檢測方式啟動。實驗結(jié)果如圖12所示。

根據(jù)圖12所示實驗結(jié)果可以看出，在未接入DCES時，儲能變流器直流母線電流存在較大幅值的波動，而DCES電容電壓波動較小。實驗結(jié)果展開圖如圖12b、圖12c所示。與之對比，在投入DCES后，直流母線電流幅值基本維持在恒定值，波動很小，而DCES電容電壓的波動幅值較大，實驗結(jié)果表明，不平衡負荷引入的低頻紋波脈動功率基本由DCES電容吸收，未進入儲能電池。因此，實驗結(jié)果驗證了DCES及控制算法的有效性。

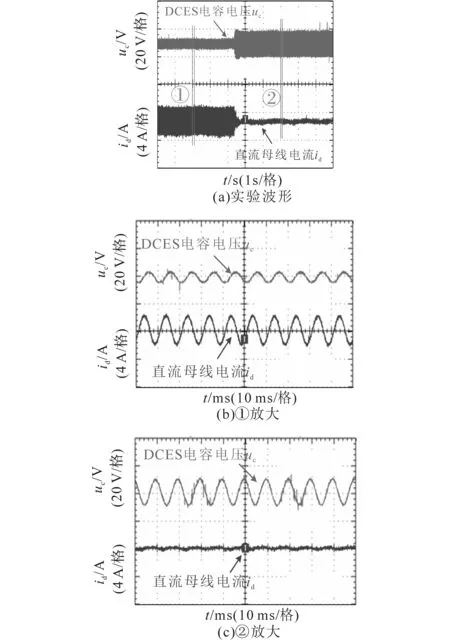
圖12 直流母線電流和DCES電容電壓實驗波形Fig.12 Waveforms of DC-bus current and DCES capacitor voltage

5 結(jié)論

本文研究了儲能變流器帶不平衡負荷時，直流母線低頻紋波電流問題的產(chǎn)生機理及有源抑制方法。利用理想情況下的兩電平變流器的開關函數(shù)等效模型，推導出直流母線電流的表達式，并指出低頻紋波電流與電網(wǎng)側(cè)所接負荷的不平衡度成正比。隨后，建立了直流電力彈簧的小信號頻域模型，并針對傳統(tǒng)PI或PR控制的局限性，給出了一種采用改進型復合控制的低頻紋波電流抑制方法，并分析了控制系統(tǒng)的穩(wěn)定性，給出了關鍵參數(shù)的設計原則。

最后，利用Matlab/Simulink仿真模型的仿真結(jié)果及等比例小型樣機實驗結(jié)果驗證了本文直流電力彈簧及控制策略的可行性。