錐體錐角變化對旋風分離器性能的影響

李 杰，馬 欣，王紅霞，鄭彥博

(1.黔南民族職業技術學院，貴州 都勻 55800，2.西南石油大學，四川 成都 610500)

0 引言

旋風分離器是一種無運動部件、結構簡單、分離性能較好的重要凈化設備。在水泥廠，石油天然氣、頁巖氣以及煤炭發電等行業有著廣泛的應用[1]。分離器內部流場極其復雜，已有很多的研究[11]。馬欣等[4]分析研究了排氣管外延長度對單級旋風分離器內部的速度流場，總壓降值以及切割粒徑的影響規律。Li等[5]創新改進排氣管的結構來優化旋風分離器的分離性能，結果表明，通過在排氣管深入段開孔，其最后的分離性能得到了相應的提高；李杰等[6]研究了排氣管內置壁面厚度對旋風分離器性能的影響，得出結論，壁面厚度為0.1D時，分離性能較好；陳啟東等[7]研究了圓柱段高度對旋風分離器性能的影響，結果表明，增加圓柱段高度，壓降顯著降低，分離效率提高。李琦等[8]研究了錐度對天然氣凈化用旋風分離器流場的影響，結果表明，在該實驗組中錐度為172°時結構最優。并未研究錐角不變，延長錐體，對分離器性能的影響。本工作主要分析了錐角不變，筒體直徑不變，延長錐體長度對旋風分離器流場及性能的影響，對旋風分離器結構設計方面具有研究意義。

1 計算模型和數值計算

1.1 結構尺寸及網格

旋風分離器幾何結構及網格示意圖如圖1所示， bz代表標準的標準stairmand型[1]，具體的結構尺寸如表1：a組旋風分離器筒體直徑保持不變，a1的筒體高度為h/2=150 mm，a2的筒體高度為a=100 mm，a3沒有筒體高度，分離器全部用錐體；b組是保持錐體的錐度不變，b1的筒體高度為h/2=150 mm，b2的筒體高度為a=100 mm，b3沒有筒體高度，分離器全部用錐體。旋風分離器bz、a1、a2、a3、b1、b2、b3的網格數依次為339818、339818、339818、339818、353160、346084、335664，網格質量均在0.6以上，能夠確保仿真的準確性和可靠性。3個截面S1、S2、S3，如圖1所示位置，分別為Z/D=2.25，2.75，3.75，其中，Z以旋風分離器的排塵口為起點。

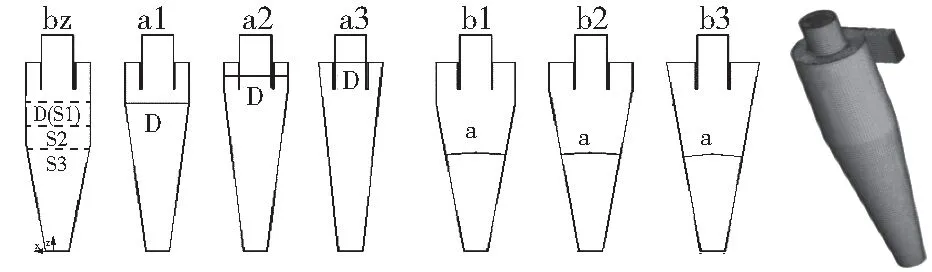
圖1 旋風分離器幾何結構圖及網格示意圖

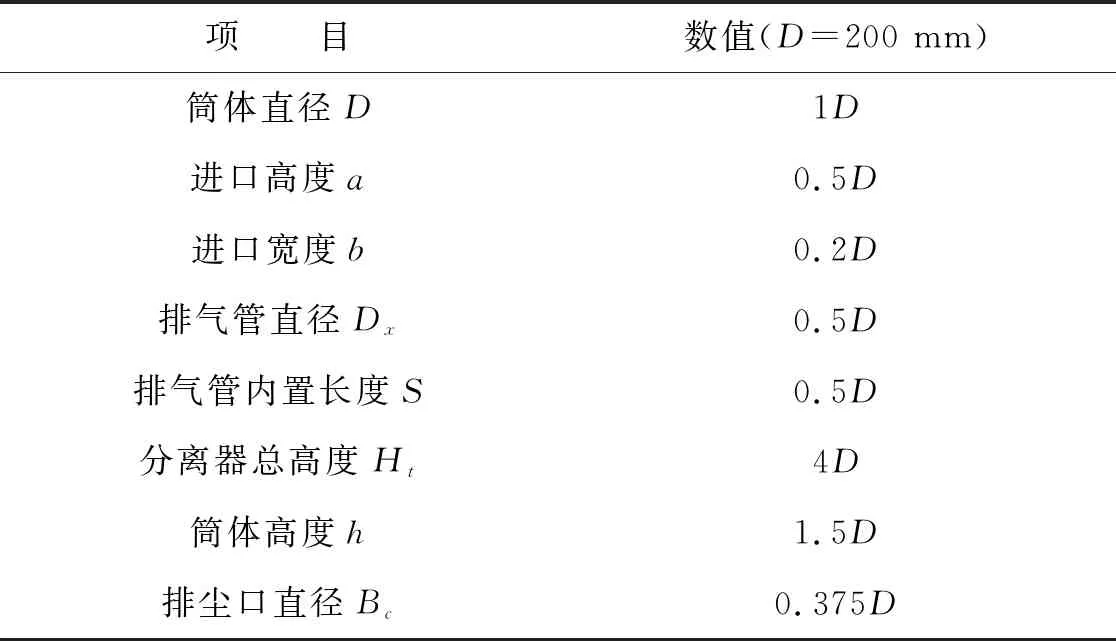
表1 旋風分離器的幾何尺寸

1.2 計算模型

旋風分離器的氣體相流域采用N-S方程和應力輸運方程采用雷諾應力模型(RSM)求解，具體計算基本方程如下：

1)連續性方程：

(1)

2)動量方程：

(2)

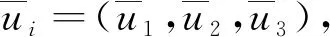
3)雷諾應力模型輸運方程

(3)

式中：擴散相，Di，j；應力產生項，Pi，j；浮力產生項，Gi，j；應力應變再分配項，Φi，j；離散相，εi，j；旋轉系統產生項，Fi，j；r自定義源項，Suser；下標i，j，k為通用坐標方向[4]。

1.3 設置邊界條件和選擇數值解法

邊界條件的設置與文獻[9]的實驗相同，氣體相設置為常溫常壓空氣，其物理化學屬性保持默認。氣體相空氣和固體相顆粒的進口速度相同：V=15 m/s，固體相顆粒密度為ρ=2700 kg/m3，質量流量設置為0.001 kg/m3；排氣管出口于氣體相設置為outflow，于顆粒相設置為escape，排氣口于顆粒相設置為trap，壁面邊界保持默認reflect[6]。湍流強度I設置為4.7%，水力直徑DH為57.2 mm。

對氣體相，本文湍流模型選用雷諾應力模型(RSM)，壓力與速度耦合選用SIMPLEC，離散格式選用QUICK，壓力插補格式選用PRESTO；對顆粒相：采用DPM方法和隨機軌道模型來處理[6]。以單相耦合計算，先進行8000步穩態求解，再進行步長為0.01，步數為400瞬態計算，得出收斂結果，進行分析。

2 數值模擬的可靠性驗證

把數值模擬結果與實驗結果進行對比分析，即把數值模擬旋風分離器內部流場的軸向速度和切向速度與實驗的進行對比驗證。Hoekstr等利用測速儀測量了旋風分離器內部流場的速度；本文數值模擬采用與文獻[2]實驗建立相同條件(幾何尺寸，進口速度)，并與之進行對比。圖2為距離排塵口942.5 mm處截面的無量綱切向速度與軸向速度的數值模擬結果與LDA實驗測量值的對比。實驗值與數值模擬的軸向速度、切向速度值基本吻合，該湍流模型和數值計算方法用來模擬旋風分離器的流場，其誤差結果范圍可接受[12]。

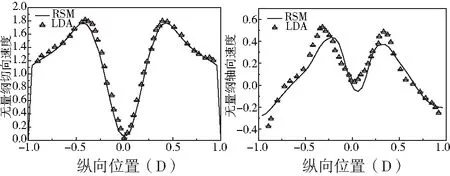
圖2 旋風分離器數值模擬值與實驗值對比結果

3 結果與分析

3.1 對旋風分離器流場的影響

3.1.1 切向速度分布

由圖3旋風分離器的切向速度云圖可看出，當筒體直徑不變時，錐體段的長度逐漸減小，筒體段長度逐漸增大，最大切向速度先增大后減小，最大值為38 m/s；當錐體的角度不變化時，隨錐體段長度逐漸增大，其最大切向速度也是先增大后減小。a1和a2的切向速度分布與標準stairmand型(bz)的切向速度分布最為相似，其中a3和b3在錐體段的渦核擺動幅度大，接近于排塵口的切向速度較大，會加劇粉塵顆粒對錐體壁面的磨損；b1和b2在排氣管下口處的切向速度云圖呈現喉結狀。由圖4切向速度曲線可以看出，a組旋風分離器在S1、S2、S3截面的切向速度總體都呈現a2>a1>bz>a3；b組旋風分離器在S1、S2、S3截面的切向速度總體都呈現b2>b1>bz>b3。通過把a組和b組與標準的stairmand型(bz)進行比較發現，錐體段延伸到旋風分離器入口高度或者說延伸到排氣管內部高度相同時，旋風分離器內部流場的切向速度最大。從切向速度曲線看只有a3旋風分離器會出現中心切向速度為負，說明在中心位置存在二次渦流現象，且二次渦流對旋風分離器的分離效率會產生一定的負影響[4]。

3.1.2 軸向速度分布

由圖3軸向速度云圖可看出，幾個模型的最大軸向速度值都出現在排氣管內；標準型(bz)與a組分離器軸向速度最大值的大小關系為a2>a1>bz>a3，標準型與b組分離器軸向速度最大值的大小關系為b3>b2>b1>bz。由曲線圖4的筒體截面S1可以看出，標準型與a組的筒體段軸向速度的大小關系為bz >a2>a1>a3，標準型與b組的筒體軸向速度的大小關系為bz >b2>b1>b3；從S2、S3截面曲線圖可以看出，a組旋風分離器與標準型的錐體段軸向速度的大小關系為a2>a1>bz>a3，同樣b組旋風分離器與標準型的錐體段軸向速度呈現b2>b1>bz>b3。呈現這種軸向速度關系的主要原因是由錐體段長度不同所導致的。

3.2 對旋風分離器壓降的影響

從圖5壓降曲線圖可看出，在a組和b組都是呈一個倒“V”形狀，隨錐體段的增長，筒體段的減短，其壓降先增加后減小。從表2可看出，旋風分離器的壓降最大值為a2和b2，以標準stairmand型為參考，壓降值的最大值增大了34.5%，壓降值的最小值降低了2.47%。產生a組和b組的壓降值變化趨勢的主要原因是由于錐體段的不斷增加，其旋流與錐體段壁面碰撞摩擦阻力增加所導致。

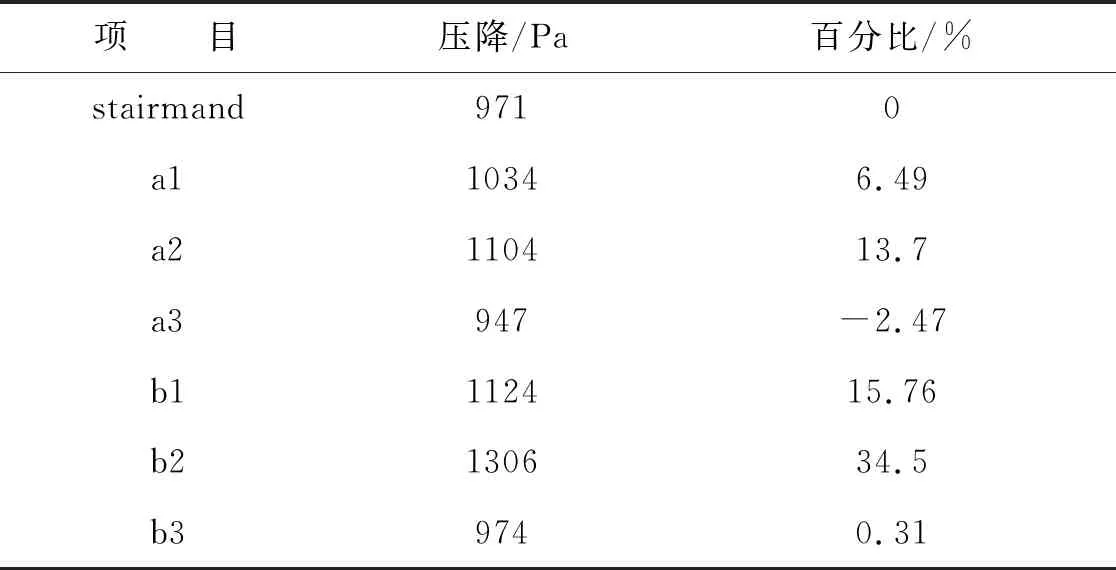
表2 bz、a組和b組旋風分離器的具體壓降

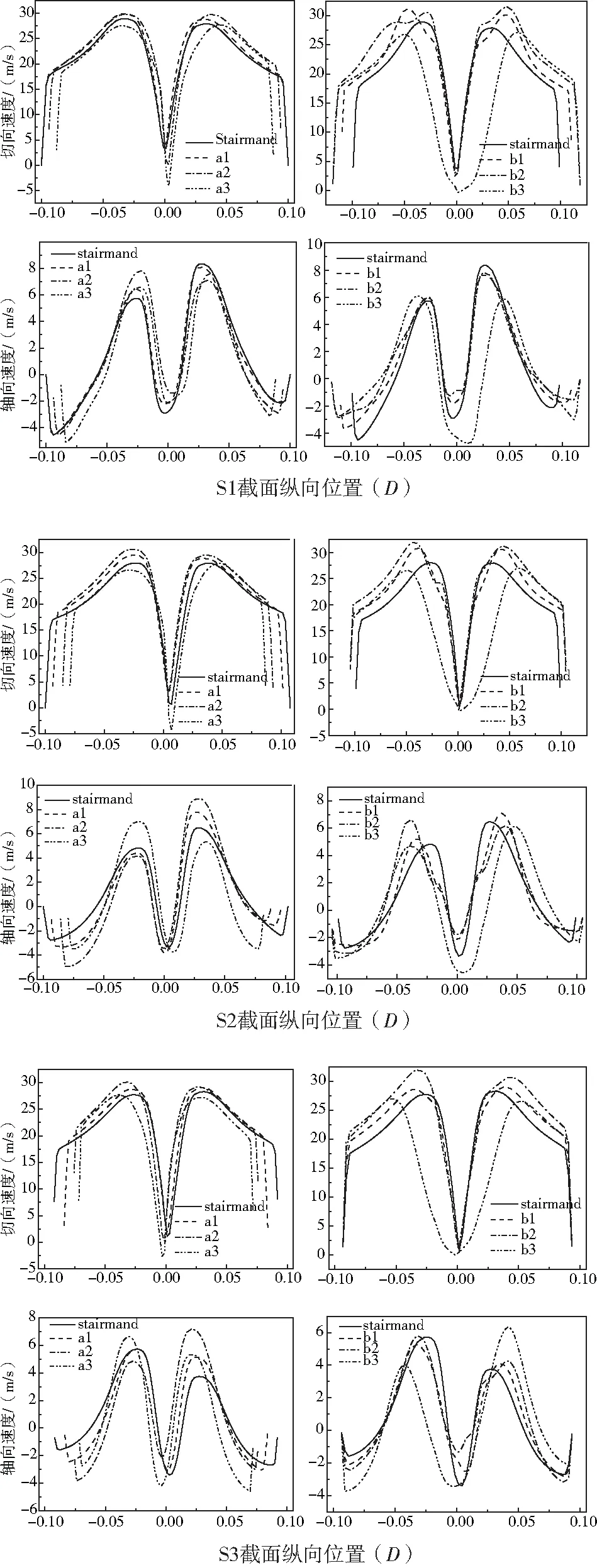
圖4 bz、a組和b組旋風分離器不同截面的切向速度和軸向速度圖

圖5 bz、a組和b組旋風分離器壓降曲線圖

3.3 對旋風分離器分離性能的影響

用切割粒徑來表征旋風分離器的分離效率，如圖6和表3所示。由圖6表3可看出，旋風分離器錐體的變化對其分離性效率有一定的影響，切割粒徑隨a組和b組的變化趨勢幾乎與壓降變化趨勢相反，呈“V”字形；隨錐體段長度逐漸增大，筒體段長度逐漸減小，切割粒徑先增大后減小；a2和b2旋風分離器的切割粒徑在各組最小，對應其分離效率最高。在錐體變化后對旋風分離器的切割粒徑除了b3外，其他模型的切割粒徑都小于標準型，即分離效率高于標準型，其主要原因是a組和b組的切線速度基本都大于標準型。a2和b2的切割粒徑為最小值，分別相對標準型分離器降低了5.97%、6.72%。綜上所述，通過流場、切割粒徑和壓降對旋風分離器的性能研究，得出結論，筒體段長度等于標準型進口高度時，旋風分離器a2和b2的分離效率最高。

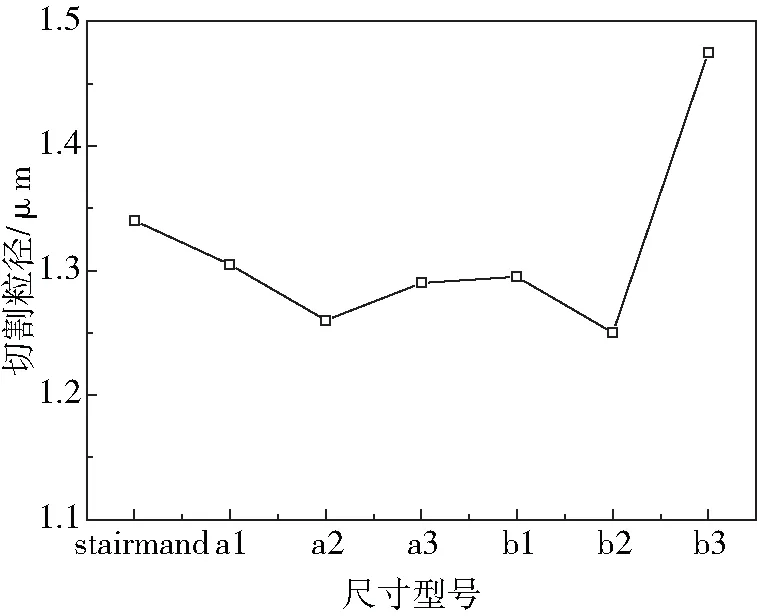
圖6 bz、a組和b組的切割粒徑的曲線圖

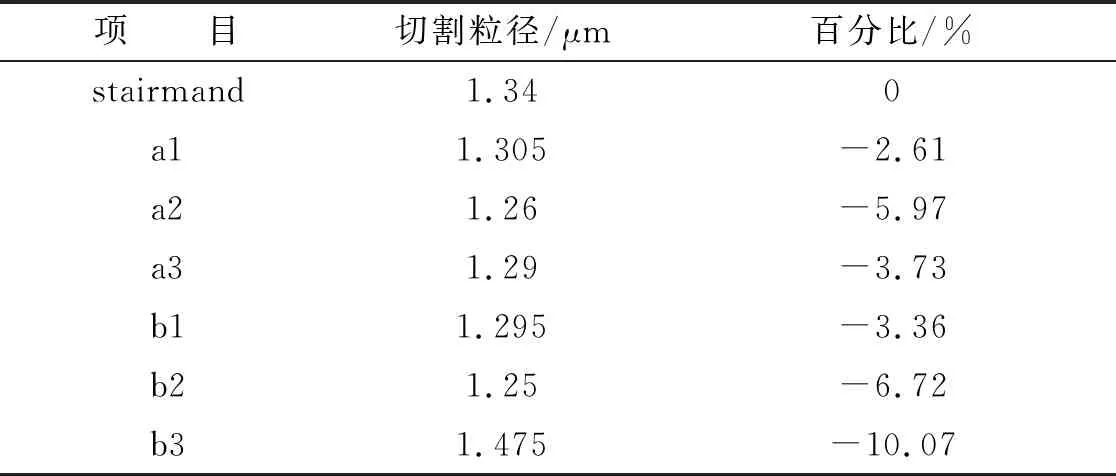
表3 bz、a組和b組的具體切割粒徑

4 小結

為了優化標準stairmand型的結構，通過數值模擬分析，得出結論：

1)a2、b2分別在a、b組的切向速度最大，并大于標準型(bz)；a2、b2分別在a、b組的軸向速度最大，卻小于bz型。a2和b2型的切向速度比標準型(bz)型大，即離心力大；軸向速度比標準型(bz)型小，即分離時間長，都有助于分離效率提高。

2)隨錐體段長度增大，筒體段長度減小，a組和b組旋風分離器的切割粒徑先增大后減小，變化趨勢幾乎與壓降變化趨勢相反，呈“V”字形，a2和b2旋風分離器的切割粒徑在各組中最小，分離效率最高，分別相對標準型(bz)降低了5.97%、6.72%。即a2和b2型的分離效率高于標準型(bz)。

3)a組和b組旋風分離器隨錐體段長度增大，筒體段長度減小，壓降先增大后減小，變化趨勢呈倒“V”形狀。以標準型(bz)為參考，a2和b2旋風分離器的壓降值為最大，分別相對標準型(bz)增大了13.7%、34.5%。即a2和b2型的壓降高于標準型(bz)。工程上應根據分離效率和壓降的綜合分析，進行設計或選型。