超高壓爆破片安全泄放裝置橡膠密封圈結構及密封性能的數值模擬

楊 超,惠 虎

(華東理工大學 機械與動力工程學院，上海 200237)

0 引言

橡膠是一種可高度變形、各向同性、壓縮性較小的聚合物材料，被廣泛用于機械、動力、汽車、石油化工和航空等領域。由于橡膠材料具有優良的超彈性能，常被用于制作密封元器件，其適用壓力也特別廣泛，靜密封的壓力范圍可從1.0×10-5MPa到400 MPa的超高壓，其密封原理是當受到外力擠壓時，橡膠密封圈依靠其自身的彈性產生較大的回彈力，將外力通過橡膠材料傳遞給接觸面，在接觸面形成接觸壓力，從而實現對容器內部介質的密封作用，用橡膠材料制作的密封元件不僅具有制造簡單、成本低廉的優勢，而且還有拆裝便捷、結構緊湊、無需螺栓預緊力的特點[1]。

但是，橡膠材料的特性非常復雜，其對外力、介質、溫度和應變速率都較為敏感，通常表現出蠕變和應力松弛等效應，因此具有較為繁瑣的材料非線性；并且，當承受較大的工作載荷時，不僅伴隨著大位移、大應變的幾何非線性，而且在實際的使用過程中，往往存在復雜的邊界條件和接觸過程的非線性問題，因此，對于橡膠制品的密封結構，其研究方法也變得十分困難。另外，橡膠材料密封圈的密封壓力理論上雖然能夠達到400 MPa，但在目前的實際工程應用中，仍然以中、低壓和真空密封為主，很少被單獨用于高壓[2]，甚至是超高壓容器及配件的密封條件，并且，橡膠材料用于高壓和超高壓密封的理論體系和結構設計規范尚不完善，因此，橡膠材料用于超高壓密封的理論和結構設計在我國仍然空白。本文就針對超高壓爆破片安全泄放裝置的密封結構，并結合橡膠材料本身的特性，展開對超高壓爆破片安全泄放裝置用橡膠密封圈結構數值模擬仿真算法的研究工作，通過穩態的靜力學分析，得到橡膠密封圈在不同結構尺寸下的內應力和接觸比壓力的分布及變化規律，并對橡膠密封圈的結構尺寸進行優化，填補我國在超高壓爆破片安全泄放裝置密封領域研究的空白。

1 自緊式橡膠密封圈的研究

超高壓爆破片安全泄放裝置的密封結構主要由爆破片、夾持器和自緊式橡膠密封圈構成，裝配結構如圖1所示。

圖1 超高壓爆破片密封結構示意Fig.1 Schematic diagram of sealing structure of ultra-highpressure bursting disc

針對超高壓爆破片安全泄放裝置的密封結構，提出一種新型的自緊式橡膠密封圈的結構型式。該密封結構主要依靠自緊式橡膠密封圈的內側面、外側面及上下側面，與爆破片和夾持器的內表面形成多個密封面。為防止超高壓爆破片安全泄放裝置在加壓初期出現低壓泄漏及向外擠出變形的情況，為此，在爆破片和夾持器之間留有預緊間隙，便于在裝配的過程中形成一定的初始密封，沒有內壓的情況下也能形成閉合密封帶，且爆破片和夾持器預緊貼合后，還能起到擋圈的作用，防止橡膠密封圈在受到內壓時出現擠出變形的失效形式。對于預緊壓縮率的確定，如果預緊壓縮率過大，就會導致密封圈內應力過大或變形嚴重而喪失原有的密封性能；如果預緊壓縮率過小，就起不到預緊的效果，預緊壓縮率ε可根據式(1)進行計算，一般情況下，預緊壓縮率在7%～30%之間選取較為合適[3]，本文取15%。

(1)

式中，H為在預緊方向上，橡膠圈的初始高度,mm；H0為在預緊方向上，密封槽預緊后的高度,mm。

在預緊載荷的作用下，自緊式橡膠密封圈發生變形，在密封面上形成一對作用力和反作用力，該作用力就是初始接觸壓力，形成一定的初始密封，在工作載荷的作用下，自緊式橡膠密封圈的密封槽在承受內部介質壓力的同時，使橡膠密封圈又發生較大變形，密封面積逐漸增加，與夾持器和爆破片之間形成工作過程中的最大接觸壓力。因此，本文將研究自緊式橡膠密封圈密封槽的寬度和高度對密封面上初始接觸壓力和在工作載荷作用下最大接觸壓力的影響，以及最大接觸壓力與介質壓力之間的關系。

2 密封失效的判斷準則

為確保橡膠密封圈及其密封結構是否安全可靠，首先確定密封結構的危險源或危險點，從而確定失效模式及失效準則。在ANSYS有限元分析中，需要采用密封失效準則來判斷密封效果的好壞，其中密封失效準則包括擠出量判據、最大剪切應力判據和最大接觸壓力判據，并需要同時滿足密封失效的三個判據。

2.1 擠出量判據

自緊式橡膠密封圈是由透鏡式密封圈改良而來，兩種密封圈最大的不同就是自緊式橡膠密封圈的內側開設了密封槽。改良前的透鏡式橡膠密封圈在預緊載荷的作用下，橡膠密封圈具有不可壓縮性，它會被擠入到介質壓力的入口側，發生較大的扭曲和擠出變形，并且，密封圈在扭曲變形的同時會發生間隙咬傷，使得密封圈在沒有進入工作狀態就已經失效，如圖2所示。因此，本文選用自緊式橡膠密封圈作為超高壓爆破片安全裝置的密封型式，并將擠出量為零作為密封失效的第一判別準則。

圖2 透鏡密封圈的扭曲變形情況Fig.2 Distortion of lens seal ring

2.2 最大接觸壓力判據[4]

在工作過程中，自緊式橡膠密封圈受到擠壓，使得自緊式橡膠密封圈與爆破片和夾持器的接觸邊界出現最大的接觸壓力，當最大接觸壓力小于工作壓力時，會導致容器內的介質泄漏，以最大接觸壓力判據可以更直觀地反映密封面上的接觸壓力與介質壓力之間的關系，如式(2)。因此，采用最大接觸壓力作為密封失效的第二判別準則。

Pmax>P

(2)

式中，Pmax為密封面上的最大接觸壓力，MPa;P為工作壓力，MPa。

2.3 最大剪切應力判據[4]

自緊式橡膠密封圈在工作過程中會產生較大的擠壓變形，使得自緊式橡膠密封圈在爆破片頂部和夾持器底部的轉角處，以及密封溝槽內的兩個轉角處產生較大的剪切應力，當剪切應力超過橡膠材料的撕裂強度時，會使密封圈發生撕裂或剪切破壞，導致密封失效，如圖3所示。因此，本文采用最大剪切應力作為密封失效的第三判別準則。

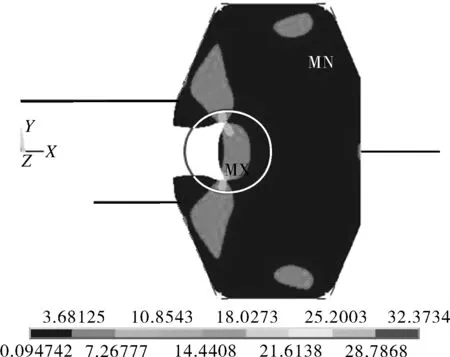
(a)

(b)圖3 自緊式橡膠密封圈的大應力部位Fig.3 High stress location of self-tightening rubber seal ring

3 爆破片安全泄放裝置密封結構的理論及數值分析

由于橡膠材料具有大位移、大應變的幾何非線性，以及復雜的邊界條件和接觸過程的非線性問題，在進行有限元數值模擬分析前，需作如下幾點假設：

(1)密封材料為近似不可壓縮的超彈性材料；

(2)密封圈材料具有確定的彈性模量和泊松比；

(3)不考慮密封圈材料松弛和蠕變效應的影響；

(4)由鋼構件制成的爆破片和夾具的剛度比橡膠材料大得多，可將爆破片和夾具視為不考慮變形的剛體，即橡膠密封圈的約束邊界；

(5)密封圈受到夾具的初始壓縮，被視為由約束邊界的指定位移引起的；

(6)橡膠材料具有各向同性，并且均勻連續；

(7)不考慮溫度變化對橡膠材料的影響。

3.1 橡膠材料本構模型的建立

在恒溫狀態下，橡膠材料具有超彈性和不可壓縮性，材料的本構關系可用下式表述：

(3)

式中，Sij為Piola-Kirchhoff應力張量分量；W為未變形體積的應變能密度函數;Eij為Lagrangian應變張量分量；Cij為Cauchy-Green變形張量分量；i,j為整數，可取0,1,2,3…。

Eij和Cij可由下式求出：

(4)

其中：δij=1(i=j),δij=0(i≠j)

式中，fij為形變梯度；Ai為材料發生形變后該質點在i方向的位置；Bi為材料未發生形變時某質點在i方向的初始位置。

由上述的本構方程可知，除了應變能密度函數W是未知數外，其余均可求得，因此，確定應變能密度函數W成為了問題的關鍵。

1940年，MOONEY[5]最早通過大量試驗證實了橡膠材料具有近似不可壓縮的特性，并且推導出應變能密度函數的計算公式：

W=C10(I1-3)+C01(I2-3)

(5)

應變能密度函數公式的推導，為當時非線性彈性理論的研究工作推進了一大步。該公式發展至今，仍然是有限元數值模擬中最常用的橡膠材料本構模型之一。在橡膠材料本構模型后續的發展中，又不斷推出了各種應變能密度函數，TRELOAR等[6]將這些研究成果分為基于分子統計學理論的統計模型和基于唯像理論的唯像模型。

首先，RIVLIN[7]在MOONEY研究的基礎上，利用級數形式推出了應變能密度函數的一般表達式:

(6)

其中，I1,I2為3個主伸長比的第一、第二不變量，其關系式為:

(7)

式中，λ1,λ2，λ3為3個主伸長比。

由于公式(6)是RIVLIN在MOONEY的基礎上推導而得，因此該式又被稱為Mooner-Rivlin模型，該模型能夠較為準確地預測橡膠材料在大變形環境下的力學行為。但該模型的計算公式較為繁瑣，計算起來相當復雜，后來又將其簡化為Neo-Hokean多項式模型，如下式：

W=C10(I1-3)

(8)

之后，YEOH[8]又根據試驗數據得出了三次方程，形成Yeoh模型，如下式：

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3

(9)

TRELOAR[9]認為，橡膠材料是由不同結構型式的線性長鏈分子交聯而成的分子鏈網絡構成，并且橡膠材料的力學性能主要取決于分子鏈網絡之間的構象熵，在外力作用下，分子鏈變形的同時改變了其中的構象熵，因此，TRELOAR基于該分子統計學理論，提出了高斯網絡模型的應變能密度函數公式:

(10)

式中，n為單位體積內的分子鏈數；k為玻爾茲曼常數，J/K；T為絕對溫度，K。

由于Treloar模型要求分子鏈末端距符合高斯分布，僅適用于小變形情況。因此，為解決該模型的缺陷，HUBERT等[10-12]分別提出了三鏈網絡模型、四鏈網絡模型和八鏈網絡模型。并且，OGDEN[13]利用TRELOAR的試驗結果，提出了可以與試驗曲線高度吻合的應變能密度函數表達式，形成了Ogden模型，如下式：

(11)

式中,ui，αi為材料常數。

通過對不同模型的分析可知，雖然高階模型對試驗曲線的擬合度更好，在大變形條件下具有較高的預測能力和準確度，但對模型初期的小變形情況誤差較大，不如低階函數的準確度高[14]，另外，利用高階模型會增加有限元的分析時間。并且，經過后續學者不斷的研究表明，對于橡膠類材料的應變能密度函數來說，一般選用雙參數的Mooney-Rivlin模型即可，該模型不僅具有較高的擬合度，而且還具有較高的計算精度。因此，綜合考慮計算成本與分析精度，本文擬采用雙參數Mooney-Rivlin模型作為橡膠材料的本構模型。

自緊式橡膠密封圈首選丁晴橡膠材料，丁晴橡膠是由丙烯氰和丁二烯聚合而成的一種合成橡膠，具有耐油和耐老化性能等特點。目前，有兩種方式可獲得丁晴橡膠材料的本構模型，一種是可以用Mooney-Rivlin的經驗公式做近似計算的方法[15-16]，但其結果的精準度難以保證；另一種是利用單軸拉伸試驗獲得的真應力-應變曲線數據，并借助ANSYS中Mooney-Rivlin二參數的擬合方法獲得Rivlin系數，ANSYS有限元軟件擬合方法的精準度較近似計算的精準度相對較高。因此，本文采用ANSYS數據擬合的方式獲取Rivlin系數，首先利用單軸拉伸的方法獲得真應力應變曲線[17](如圖4所示)，然后將數據輸入到ANSYS有限元軟件直接擬合出丁晴橡膠Rivlin系數，C10=1.702 MPa，C01=-0.02 MPa，同時根據應力-應變曲線，得到丁晴橡膠的彈性模量為11.4 MPa，泊松比為0.499，丁晴橡膠的抗拉強度一般在30～40 MPa，本文取其許用應力為15 MPa。

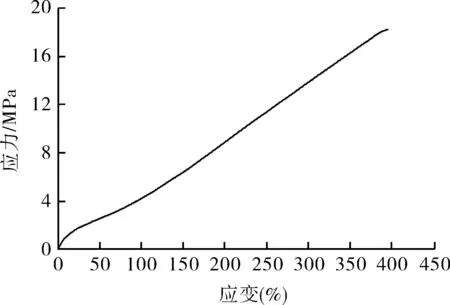
圖4 丁晴橡膠應力-應變曲線Fig.4 Butadiene rubber stress-strain curve

3.2 非線性力學分析模型

對自緊式橡膠密封圈進行有限元分析時，鑒于密封圈本身為軸對稱結構，并且，爆破片和夾具與自緊式橡膠密封圈之間的材料、邊界條件和幾何形狀也都符合軸對稱條件，因此可將自緊式橡膠密封圈的模型簡化為ANSYS二維軸對稱模型，通過平面軸對稱模型來模擬三維對稱結構。同時，根據爆破片和夾具之間密封槽的寬度，建立的自緊式橡膠密封圈的軸對稱模型的壁厚分別為9,12,15,18 mm。

劃分網格時，自緊式橡膠密封圈選用Plane 182單元，該單元是二維四節點實體單元，并具有超彈性、應力剛度、塑性、大應變和大變形的能力，是適合模擬近似不可壓縮的橡膠材料。在進行網格劃分前，首先定義單元特性和單元計算公式，分別設置為軸對稱單元和力-位移混合公式，并對網格的平滑度和長寬比進行設定和調整。另外，爆破片和夾具等鋼結構與橡膠材料的剛度相差較大，因此，將爆破片和夾具簡化為剛體邊界，剛體單元為虛擬單元而非實體單元，其單元類型是由柔體接觸單元Conta 172和剛體目標單元Targe 169的接觸對單元組成，自緊式橡膠密封圈的網格劃分如圖5所示。

圖5 自緊式橡膠密封圈數值模型Fig.5 Numerical model of self-tightening rubber seal ring

3.3 接觸方法

在預緊和密封的過程中，自緊式橡膠密封圈在大變形的過程中會使得其與夾持器和爆破片之間形成接觸區域，而有限元分析中的接觸分析是密封圈數值模擬過程中的關鍵點。在有限元分析的接觸算法中，為用戶提供了罰函數法(Penalty method)、拉格朗日乘子法(Lagrange & penalty method)、增進的拉格朗日方法(Augmented Lagrange method)、內部多點約束法(MPC algorithm)和純拉格朗日乘子法(Lagrange method)[18-19]。在通用的接觸分析計算中，最常用的是前3種接觸分析算法。

罰函數法一般通過接觸面和接觸力之間的接觸位移建立位移和力之間的線性關系，接觸位移在ANSYS程序中通過分離接觸體中節點之間的距離進行計算。從理論上說，接觸剛度大則接觸位移小，接觸剛度為無窮大時，則為零接觸，但在實際情況中，隨著接觸位移的減小，其剛度矩陣的收斂性也變得越來越差，甚至不收斂；反之，隨著接觸剛度的變小，其剛度矩陣也會有所改善，但接觸位移也隨之增大，其后果是增大最終的計算誤差。因此，要不斷地更正接觸剛度和接觸位移，反復試算，才能確定合適的接觸剛度。

在增進的拉格朗日法中，ANSYS程序是從罰函數開始，找到精確的拉格朗日乘子，對罰函數進行一些列修正迭代。與罰函數相比，拉格朗日乘子容易得到良態條件，對接觸剛度的敏感性較小。然而，在有些分析中，增進的拉格朗日法可能需要更多的迭代次數，特別是變形后網格發生畸形或是過于扭曲變形的情況。

拉格朗日乘子法與前兩種方法不同，它是將接觸力作為獨立的自由度進行計算，不需要定義接觸剛度來推算合適的接觸位移，從而避免了因接觸位移過大而產生的計算誤差，此法可實現接觸位移為零的真實接觸條件。但該方法中的剛度矩陣具有零對角元，在求解器的選擇上具有一定的限制，只能使用直接法求解器。另外，對于接觸狀態發生變化時，例如接觸狀態從接觸到分離，然后由分離再到接觸的交替式改變，拉格朗日法難以解決。

綜上所述，為提高數值模擬的計算精度，并避免由于接觸位移的確定而引起的計算誤差，本文采用拉格朗日乘子法對自緊式橡膠密封圈進行接觸分析，并利用高斯點對接觸位置進行接觸檢測。

3.4 載荷及邊界條件的施加

超高壓爆破片的密封結構在開始工作時一般分為兩個步驟，首先是將自緊式橡膠密封圈安裝在夾持器和爆破片之間的密封槽內進行初始密封，然后向密封空間注入壓力介質。因此，在有限元仿真過程中也按照兩個步驟進行。

第一步：模擬自緊式橡膠密封圈安裝的過程，首先對夾持器施加全方向的固支約束，使其起到固定位置的作用；然后根據夾持器和爆破片之間的預緊間隙，對爆破片施加Y方向的間隙位移；最后對爆破片施加X方向的固定約束。

第二步：在所有與介質接觸的自緊式橡膠密封圈施加介質壓力，以此模擬自緊式橡膠密封圈的工作狀態，確保介質壓力與接觸表面相垂直，施加的介質壓力如圖5箭頭的區域。

3.5 網格重構技術的應用

自緊式橡膠密封圈在預緊載荷的作用下會發生大的扭曲變形，特別是溝槽兩個轉角處的網格發生較大的畸變扭曲，使得在有限元分析的過程中，由于網格畸變而無法收斂導致計算終止。ANSYS有限元軟件中提供的網格重構技術很好地解決了這個問題，網格重構技術不僅能夠解決網格畸變無法收斂的問題，而且還能對原有網格進行細化，提高計算精度。本文就利用網格重構技術對施加預緊載荷以后發生畸變的位置，特別是溝槽的兩個轉角處的網格，進行網格再劃分。如圖6所示。

圖6 網格重構技術Fig.6 Mesh reconstruction technique

3.6 密封槽寬度的變化對密封性能的影響

3.6.1 預緊載荷下Mises應力和初始接觸壓力的變化

為了尋求密封槽寬度對密封性能規律性的影響，本節選取4種尺寸的自緊式橡膠密封圈，其厚度分別為9,12,15,18 mm，預緊壓縮率均為15%，密封槽寬度與密封槽厚度的比值在0.1～0.9的范圍內，每0.05取一個比值作為密封槽的寬度，每個厚度尺寸的橡膠密封圈分別設置17個尺寸。首先對其分別施加預緊位移載荷，進行有限元數值建模分析，由于篇幅有限，本節僅展示部分數值模擬的結果，用以展示自緊式橡膠密封圈在預緊載荷作用下的變形和應力狀態，如圖7所示。從圖7可以看出，當密封槽寬度與密封槽厚度的比值為0.1時，自緊式橡膠密封圈在預緊載荷的作用下，仍然會被擠出到壓力介質的入口側，造成較大的扭曲和擠出變形，并在爆破片和夾持器的轉角處伴隨有較大的Mises應力，可能會造成剪切破壞；當密封槽寬度與密封槽厚度的比值為0.3時，雖然自緊式橡膠密封圈在預緊載荷作用下未被擠出發生扭曲變形，但由于密封槽寬度尺寸太小，自緊式橡膠密封圈在預緊載荷的擠壓作用下，密封槽出現較大且不規則的褶皺擠壓變形，使得密封圈溝槽圓角處的應力過大，在此處發生應力破壞的可能性較大。

為了能更為直觀地分析4種尺寸的自緊式橡膠密封圈在不同密封槽寬度尺寸條件下，其Mises應力在預緊載荷作用下的變化情況，本文將4種尺寸密封圈的應力狀態示于圖8的曲線中。

水平托輥安裝在左、右支板兩側，由于左、右支板固定托輥軸孔為封閉孔。每次更換任一水平托輥時，均需拆卸左、右支板的固定螺栓，將左、右支板及全部托輥從電動鏟運后尾架取出，然后再進行更換安裝。

(a)b/t=0.1,t=9 mm

(b)b/t=0.7,t=18 mm圖7 自緊式橡膠密封圈應力云圖Fig.7 Stress nephogram of self-tightening rubber seal ring

圖8 Mises應力隨密封槽寬度變化的關系曲線Fig.8 Mises stress curve as a function of seal groove width

通過圖8可知，隨著密封槽寬度和密封圈厚度的比值不斷增大，其Mises應力先增大、后又不斷減小，其原因是由于隨著比值的增大，影響密封圈Mises應力的主導因素在不斷變化。當比值在0.1～0.3之間時，主要影響Mises應力的是由于橡膠密封圈的擠出扭曲變形引起的，其應力最大部位主要在爆破片和夾持器轉角部分對橡膠圈造成的剪切破壞；當比值在0.3～0.5之間時，主要影響Mises應力的是由于橡膠密封圈密封槽2個轉角處不規則的褶皺畸變引起的，褶皺使轉角處的橡膠材料發生近乎45°的大扭曲變形；當比值大于0.5時，橡膠密封圈的擠出變形和褶皺畸變都漸漸消失，對橡膠圈Mises應力起主導作用的是在預緊載荷作用下對橡膠圈輕微的彎曲變形造成的。通過圖8還可以看出，當密封槽寬度與密封槽厚度的比值大于0.5時，橡膠密封圈的Mises應力小于丁晴橡膠的許用應力，因此，當預緊壓縮率為15%時，自緊式橡膠密封圈密封槽寬度和厚度的比值應大于等于0.5。

圖9示出了自緊式橡膠密封圈密封槽寬度和厚度的比值大于等于0.5時，初始密封接觸壓力的變化情況。

圖9 初始接觸壓力隨密封槽寬度變化的關系曲線Fig.9 Curve of initial contact pressure as a functionof seal groove width

圖10 初始接觸壓力情況Fig.10 Initial contact pressure

從圖9可以看出，隨著密封槽寬度和厚度比值的不斷增大，初始密封接觸壓力不斷減小，其原因是由于當密封槽寬度不斷增大的同時，自緊式橡膠密封圈抵抗預緊載荷變形的能力越來越小，因此初始密封接觸壓力也隨之減小。但是，當初始密封接觸壓力小到一定程度時，自緊式密封圈內側面和外側面的初始接觸壓力相對上下兩個面將非常小，初始密封的效果會大打折扣，如圖10所示，在工作初期還可能會出現低壓泄漏的情況，因此，本文根據數值模擬情況，將初始密封接觸壓力定為不小于2 MPa。因此，自緊式橡膠密封圈密封槽寬度和厚度的比值應在0.5～0.65之間選取。

3.6.2 工作載荷下最大接觸壓力的變化

基于上文數值模擬給出的計算結果，橡膠密封圈密封槽寬度和厚度的比值在0.5～0.65的范圍內，每隔0.05取一個值作為密封槽的寬度，每個厚度的密封圈共設置4個密封槽跨度尺寸。同時，針對不同尺寸的密封圈分別施加100,150,200,250，300 MPa的介質壓力，分別對其進行有限元數值模擬分析。由于篇幅有限，本節只示出部分模擬結果，用以展現在不同介質壓力下，接觸壓力的分布情況，如圖11所示。由圖11可以看出，自緊式橡膠密封圈在工作載荷的作用下，發生了較大的變形，密封面積達到最大化，并且8個密封面的接觸壓力均為最大值，最大接觸壓力均大于介質壓力。

(a)t=9 mm,b/t=0.6,P=300 MPa (b)t=18 mm,b/t=0.6,P=300 MPa

圖12 最大接觸壓力隨密封槽寬度變化的關系曲線Fig.12 Curve of maximum contact pressure as a functionof seal groove width

圖12示出了不同介質壓力下自緊式橡膠密封圈的接觸壓力，當密封圈密封槽寬度與厚度的比值在0.5～0.65的范圍內，其接觸壓力均大于各自的介質壓力，因此可證明自緊式橡膠密封圈在超高壓工況下能夠很好地起到自緊式密封的作用。

3.7 密封槽高度對密封性能的影響

3.7.1 預緊載荷下Mises應力和接觸壓力的變化

圖13 密封圈預緊后發生干涉云圖Fig.13 Nephogram of interference after pretightening of seal ring

由于篇幅有限，本節僅示出部分數值模擬的結果，用以展示自緊式橡膠密封圈在預緊載荷作用下的變形和應力狀態，如圖14所示。可以看出，由于在預緊載荷作用下，自緊式橡膠密封圈發生彎曲變形，特別是其溝槽圓角處變形較大，因此也伴隨有較大的Mises應力。

圖15示出了自緊式橡膠密封圈在不同密封槽高度時的應力情況。密封槽高度與密封圈高度比值在0.2～0.6之間的Mises應力均小于丁晴橡膠的許用應力，滿足撕裂強度要求。

(a)h/H=0.2,t=9 mm (b)h/H=0.6,t=18 mm

圖15 Mises應力隨密封槽高度變化曲線Fig.15 Mises stress curve as a function of seal groove height

圖16示出了自緊式橡膠密封圈初始密封接觸壓力的變化情況。可以看出，隨著密封槽高度的不斷增大，初始密封接觸壓力不斷減小，其原因是由于當密封槽高度不斷增大的同時，自緊式橡膠密封圈抵抗預緊載荷變形的能力越來越小，因此初始密封接觸壓力也隨之減小。同時，為防止工作初期出現低壓泄漏的情況，本文將初始密封接觸壓力定為不小于2 MPa。因此，自緊式橡膠密封圈密封槽高度和密封圈高度的比值在0.2～0.4之間選取較為合理，并且，同時滿足密封槽高度為預緊位移的3～4倍。

圖16 初始接觸壓力隨密封槽高度變化的關系曲線Fig.16 Curve of initial contact pressure as a functionof seal groove height

3.7.2 工作載荷下最大接觸壓力的變化

基于以上數值模擬給出的計算結果，本節在密封槽和密封圈高度比值為0.2～0.4的范圍內，每隔0.05取一個值作為密封槽的寬度，每個厚度的密封圈共設置5個密封槽跨度尺寸。同時，針對不同尺寸的密封圈分別施加100,150,200,250，300 MPa的介質壓力，分別對其進行有限元數值模擬分析。由于篇幅有限，本節只示出部分模擬結果，用以展現在不同介質壓力下，接觸壓力的分布情況，如圖17所示。可以看出，自緊式橡膠密封圈的8個密封面的接觸壓力均為最大值，并且最大的接觸壓力均大于介質壓力。

(a)t=9 mm,h/H=0.3,P=300 MPa (b)t=12 mm,h/H=0.3,P=300 MPa

圖18示出了不同介質壓力下自緊式橡膠密封圈的最大接觸壓力，當自緊式橡膠密封圈密封槽高度與密封圈高度的比值在0.2～0.4的范圍內，其接觸壓力均大于各自的介質壓力，因此可證明自緊式橡膠密封圈在超高壓工況下，能夠很好地起到自緊式密封的作用。

圖18 最大接觸壓力隨密封槽高度變化的關系曲線Fig.18 Curve of maximum contact pressure as a functionof seal groove height

4 結語

利用ANSYS有限元數值模擬分析中的雙參數Mooney-Rivlin應變能密度函數，建立了丁晴橡膠材料自緊式橡膠密封圈的本構方程，利用拉格朗日乘子算法，對爆破片、自緊式橡膠密封圈和夾持器進行數據建模，采用ANSYS軟件中特有的網格重構技術，對數據模型的網格進行重新劃分，避免了由于網格發生畸變導致數據無法收斂的問題。

同時，又借助擠出量、最大接觸壓力和最大剪切應力等判別原則，得到了橡膠材料自緊式橡膠密封圈密封槽寬度和高度對密封性能的影響，以及最佳的開槽尺寸和確定方法：(1)自緊式橡膠密封圈密封槽寬度和厚度的比值宜在0.5～0.65之間選取；(2)自緊式橡膠密封圈密封槽高度和密封圈高度的比值宜在0.2～0.4之間選取，并且，需同時滿足密封槽高度為預緊位移的3～4倍。

該方法和確定原則為后續自緊式橡膠密封圈的研究提供了理論基礎，為我國其他種類的橡膠密封圈的結構型式設計又提出了新的思路和研究方法。