水平-豎直管道內水流沖擊滯留氣團的三維數值模擬研究

盧坤銘

(中國三峽建工(集團)有限公司，四川 成都 610041)

0 引 言

實際輸水管道系統的啟動填充過程中常會發生水流沖擊滯留氣團的復雜瞬變流，極易引起異常壓力波動，影響系統安全運行甚至導致爆管事故[1-3]。

該瞬變流現象引起了很多學者的廣泛關注。Martin[4]首次建立了水流沖擊滯留氣團現象的剛性水體數學模型，但其模型沒有考慮水氣交界面的運動。Izquierdo等[5]對Martin[4]的剛性數學模型進行了改進，考慮水氣交界面位置動態變化，建立充水排氣的剛性數學模型，并指出水體間滯留氣團的快速壓縮會引起異常壓力升高。Liou等[6]針對起伏管道系統中初始時上游閥后完全放空的充水過程，建立了相應的剛性數學模型，但未考慮滯留氣團的影響。劉德有等[7]建立了起伏變特性管道系統中水流沖擊單個氣團的剛性數學模型。剛性模型具有簡單、快捷的優點，但其應用具有一定的局限性，如滯留氣團含量較小時，可能會得到錯誤結論。Chaiko等[1]考慮水體和管道的彈性，建立了三種彈性數學模型，并給出了各彈性模型的適用范圍。其他學者[8-13]研究了水流沖擊滯留氣團的瞬變壓力及參數變化規律，發現水氣耦合作用機理復雜，且可能引起十倍于入口壓力的危險峰值壓力；同時，提出了“剛性塞”、“虛擬塞”等方法，建立了彈性水體模型。

本文針對水平-豎直管道啟動填充過程中含滯留氣團瞬變現象，考慮了水體彈性、氣體可壓縮性、水-氣交界面的動態運動，建立了相應的三維CFD數學模型。通過模型計算與實驗結果對比，驗證了所建模型能夠有效地預測快速充水過程中含滯留氣團的壓力變化；同時，研究該瞬變過程中氣團長度、湍流模型、管壁粗糙度等參數動態變化規律。

1 實驗研究

針對水平-豎直管道內水流沖擊滯留氣團的瞬變流現象，設計搭建了如圖1所示的實驗系統。整個系統主要由潛水泵、氣壓罐、電磁流量計、球閥、管道、空氣閥等組成。整個系統從上游至下游依次由蓄水池、不銹鋼多級潛水泵、螺紋式球閥、氣罐(壓力罐)、電磁流量計、球閥、進氣孔口、泄水閥、完全封閉的末端組成。水泵與氣罐之間通過不銹鋼鋼管連接，壓力罐至下游由一段1 m長的不銹鋼和多段有機玻璃透明管道組成。從氣罐出口至管道末端為水流沖擊滯留氣團的實驗研究管道，其總長為8.862 m，其中，有機玻璃管道內徑4 cm，壁厚1 cm。本實驗中，將水平管道中心線定為Z=0，共安裝8個壓力傳感器(Pressure Transducer，PT)和1個溫度傳感器，各裝置位置參數如表1所示。在最底部分別安裝2個排水閥，僅用于調節初始狀態下氣團長度，但在瞬變過程中均處于關閉狀態。各壓力傳感器性能一致，測量范圍：0～0.5 MPa。電磁流量計性能參數，公稱通徑為DN40，流量范圍0～25 m3/h。數據采集系統為美國國家儀(NI有限公司產品PCI-6221，采樣率250 kSps/s)。

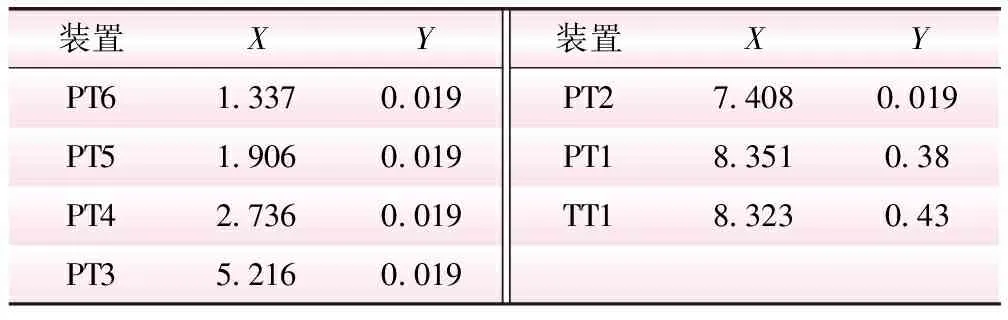
表1 水平-豎直管道傳感器位置 m

水流沖擊管道內含滯留氣團的動態特性與氣團長度、湍流模型、管壁粗糙度、入口壓力等參數有關，對于水平-豎直管道與各種參數的相互關系研究很少。表2給出了水流沖擊水平-豎直管道內含一段滯留氣團的模擬工況參數，分析了系統壓力峰值、波動周期與各參數的相互關系規律。初始時所有閥門關閉，球閥快速開啟以實現水流沖擊氣團瞬變過程，球閥開啟時間0.1 s。

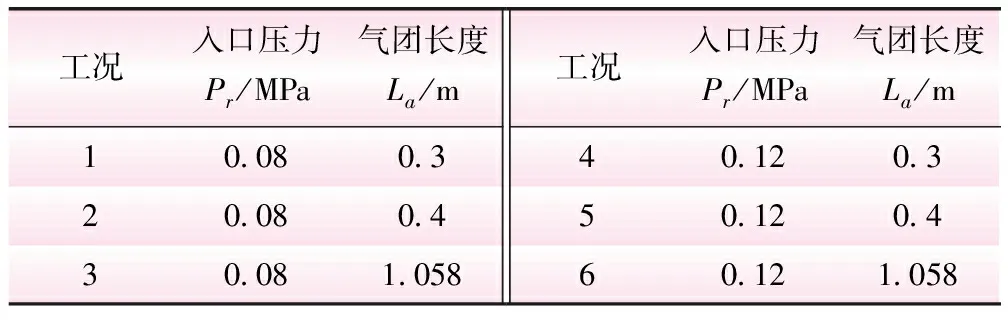
表2 水平-豎直管道模擬工況參數

2 數值模擬

2.1 控制方程

采用VOF模型追蹤水氣交界面，三維模型的基本控制方程為

連續性方程

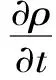
(1)

能量方程

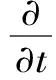
(2)

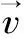
模擬中，氣體、水體均為可壓縮狀態。假定氣體遵循理想氣體定律，水體狀態方程為

(3)

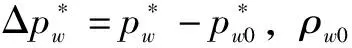
數值模型中，考慮了水氣兩相間的熱傳導、流體與固體壁面間的對流以及固體壁面內的熱阻等可能存在的熱效應，傳導熱流由傅里葉定律公式確定，即

q″cond=-λ?T

(4)

式中，λ為介質(空氣、水或壁面)的熱傳導系數，對于氣相和液相之間的熱傳導用λeff代替λ。

對流傳熱項由牛頓冷卻定律確定，即

q″conv=h(Ts-Tf)

(5)

式中，h為局部對流傳熱系數；Ts為壁面溫度；Tf為流體溫度。

壁面傳導熱阻公式為

(6)

式中，e為壁面厚度；kwall為壁面熱傳導系數。

2.2 湍流模型

本文對比了Standardk-ε、RNGk-ε這兩種湍流模型計算結果。兩種模型都適用于湍流，分子之間的黏性可以忽略，區別在于計算湍流黏性的方法不同以及控制湍流擴散的普朗特數不同，Standardk-ε湍流模型適合完全湍流的流動過程模擬，RNGk-ε則針對高雷諾數流動問題。

2.3 數值求解格式及邊界條件

該模擬選用三維雙精度求解器。采用有限體積法(FVM)進行網格離散，速度、壓力和密度的耦合方法選擇PISO算法，壓力項采用PRESTO格式，動量項、能量項采用二階迎風格式，體積分數采用Geo-Reconstruct格式進行離散，時間差分采用一階隱式格式，殘差收斂值為10-6，時間步長為0.000 1 s，計算時長3 s。

邊界條件為壓力罐下部Patch為有壓水體，阻斷水體及氣團均為大氣壓。閥門區域采用動網格模型，閥門開啟時間為0.1 s。上游管道出口與閥門進口、閥門出口與起伏管道進口設置為2對“interface”邊界條件，其他均為默認邊界條件。

2.4 網格無關性分析

本次數值模擬采用六面體結構化網格，其可以更好地適用于復雜的流動邊界。針對工況1，采用3種不同數量網格進行數值模擬計算并與實驗結果對比分析驗證，得出計算耗時與壓力誤差。通過改變網格節點數獲取不同網格數量，分別為26.2萬、33.2萬、53.8萬，對應的壓力峰值與實驗結果的誤差分別為0.7%、0.45%和0.2%。基于模擬精度與計算時間的考慮，最終選用網格數量為33.2萬的網格。

3 參數分析

3.1 氣團長度的影響

圖2給出了表2中所有工況的數值模擬結果和實驗結果對比。由圖2可知，模擬結果的壓力幅值與波動周期都與實驗結果吻合較好，特別是第1峰值結果與實驗幾乎完全吻合。對于第2壓力峰值，隨著氣團長度的增加，模擬結果與實驗結果的誤差越來越小。原因可能是因為在數值模擬過程中采用了光滑壁面，同時忽略了法蘭、流量計等的局部損失，導致計算的摩阻比實際結果小，而這一損失在流體流過管壁時顯然不同。

水流快速沖擊氣團的過程中，能量耗散主要以熱傳導、水力機械損失為主。當初始氣團長度較長時，可以觀察到在水平-豎直管道的彎管處有非常劇烈的水氣兩相作用，水氣交界面呈現不規則變化，這將導致能量主要以熱量損失為主，熱量耗散占總體能量損失的比重較大，而粘性耗散相對較小。當氣團長度較短時，因為氣團壓縮膨脹路徑較短，氣-水交界面在豎直管道內趨于穩定，且在整個過程中幾乎垂直于管道中心線，這表明對于該工況的能量耗散中以熱量損失的比例降低，主要以摩阻損失為主。同一入口壓力下，隨氣團長度減小，整個系統壓力峰值增大，且增值隨著入口壓力的增大而逐漸減小，說明長氣團工況對整個系統起到一定的緩沖作用。由圖2可知，同一氣團長度下，不同入口壓力氣團壓力峰值之差分別為169.23、165.24、149.51 kPa，遠大于入口壓力增值40 kPa，說明入口壓力越大系統壓力峰值越大，且峰值增值遠大于系統入口壓力增值。

圖2 不同氣團長度情況下，水平-豎直管道內PT1處壓力計算結果與實驗結果對比

3.2 湍流模型的影響

圖3給出了工況1、2、3、6時，不同湍流模型下，數值模擬結果與實驗結果的對比結果。

圖3 不同湍流模型下，水平-豎直管道PT1處壓力計算結果與實驗結果對比

由圖3可知，4種工況在兩種不同湍流模型下的數值模擬結果與實驗結果都十分吻合，但是仍與實驗結果存在一定的誤差，為了能夠準確地選擇湍流模型進行計算分析，采用一定的數據統計方法對各工況進行分析，相對誤差采用下式計算：

(7)

式中，Hexp為實驗工況下最高壓力；HCFD為數值模擬下最高壓力。

由圖3a、3b、3c對比可知，在同一較小入口壓力(Pr=0.08 MPa)作用下，3種工況在Standardk-ε湍流模型下的第一壓力峰值相對誤差分別為1.99%、0.05%、4.82%，在RNGk-ε湍流模型下的第1壓力峰值相對誤差分別為7.64%、4.43%、4.02%。可以明顯看出對于較短滯留氣團，Standardk-ε湍流模型能夠更準確地模擬第1壓力峰值。對于氣團較長的工況3而言，兩種湍流模型的相對誤差都大于4%，Standardk-ε湍流模型的計算結果低于實驗結果，RNGk-ε湍流模型的結果則高于實驗值。可能的原因是由于在低入口壓力較長氣團工況下，整個管道的紊流發展不充分，系統能量的損失主要以摩阻損失為主，但是兩種湍流模型的應用場景更多的是充分發展的湍流。從波動周期分析，Standardk-ε湍流模型下3種工況的模擬結果均與實驗吻合較好。由圖3a、3c對比可知，Standardk-ε湍流模型能夠很好地模擬前兩個波動周期，從第3個周期開始，工況1滯后實驗值，工況3提前實驗結果，這是因為氣團較短，水氣耦合作用增強，氣團運動速度加快，而氣團較長時，氣團壓縮、膨脹過程需要更長時間，導致波動周期滯后。

由圖3c、3d對比可知，在同一較長氣團(La0=1.058 m)不同壓力作用下，2種工況在Standardk-ε湍流模型下的第一壓力峰值相對誤差分別為4.82%和6.8%，在RNGk-ε湍流模型下的第一壓力峰值相對誤差分別為4.02%和2.33%。可以明顯看出對于較長滯留氣團，RNGk-ε湍流模型能夠更準確地模擬第一壓力峰值，且入口壓力越大，Standardk-ε湍流模型的誤差就越大，其誤差已經超過5%，可能的原因是入口壓力越大，隨著球閥的漸進式開啟，較小開度時在管壁方向會產生射流，開度逐漸加大，射流逐漸充分發展，速度越來越大，使得滯留氣團在水平和豎直管道內的速度分布不均，氣團在軸向和徑向的運動速度不同，產生不對稱壓縮現象，這非常符合RNGk-ε湍流模型的高應變率和大曲率修正，因此RNGk-ε湍流模型的模擬結果更好。從波動周期分析，2種工況中RNGk-ε湍流模型的第一壓力響應時間比Standardk-ε湍流模型分別提前0.032、0.048 5 s，且RNGk-ε湍流模型與實驗結果的誤差都在1%以內，入口壓力越大，波動周期提前時間更長，與實驗結果吻合更好。

3.3 管壁粗糙度的影響

圖4給出了不同粗糙度下，工況4和工況6中PT1壓力計算結果和實驗結果對比。由圖4a、4c可知，隨著管壁粗糙度增加，兩種工況第1、2壓力峰值與實驗結果的差值逐漸增大，但兩者還是存在一定差異，分析如下：對于工況4，當管壁粗糙度為0.01、0.1 mm時，第1、2壓力峰值的數值模擬結果均高于實驗值，且由于管壁粗糙度引起的能量耗散可以忽略不計，當粗糙度為0.5、1 mm時，壓力峰值開始出現較大衰減，且隨著粗糙度的增加衰減值也逐漸增大，第2壓力峰值的衰減程度大于第1壓力峰值。圖4b為粗糙度對第1、2壓力峰值的敏感性分析，隨著粗糙度的增加，第2壓力峰值對粗糙度的敏感性高于第1壓力峰值，其平均衰減程度為10.15%，而第1壓力峰值的平均衰減程度為5.92%，兩者接近兩倍關系，說明對于小氣團工況，增加壁面粗糙度高度，主要作用于第2個壓力峰值。

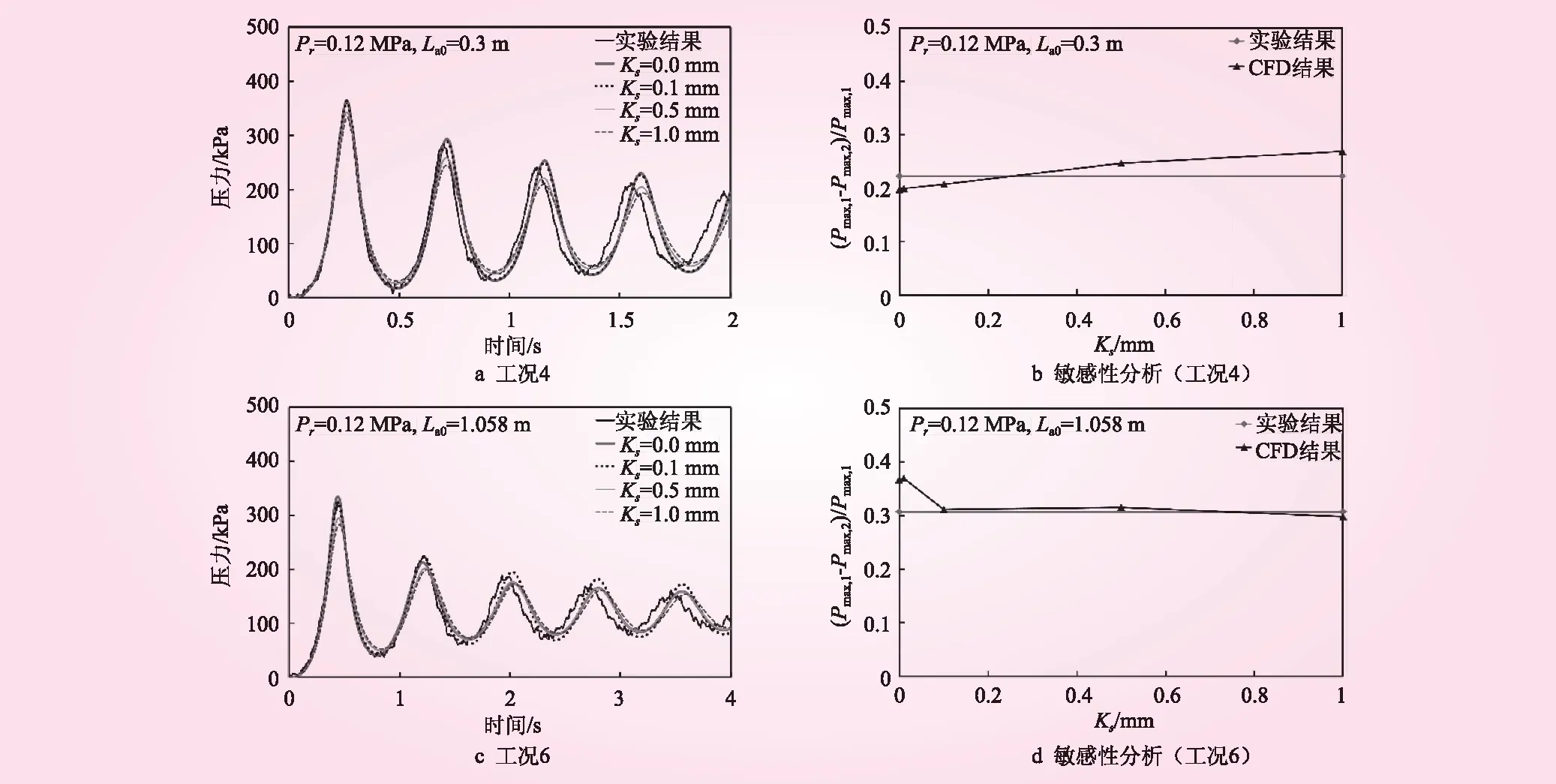
圖4 不同粗糙度，水平-豎直管道PT1處壓力計算結果與實驗結果對比

對于工況6，類似于工況4，當管壁粗糙度小于0.5 mm時，第1壓力峰值數值模擬結果高于實驗結果，平均高8.05 kPa，而第2壓力峰值的結果與實驗值吻合較好，因此管壁粗糙度引起的能量耗散可以忽略不計。隨著粗糙度逐漸增大至0.5 mm和1 mm時，兩個峰值均開始出現壓力衰減，且隨著粗糙度的增加衰減值逐漸增大。由圖4d敏感性分析可知，第1壓力峰值對粗糙度的敏感性高于第2壓力峰值，因此第1壓力峰值的衰減值大于第2壓力峰值衰減值。第1壓力峰值平均衰減10.44%，衰減值為33.72 kPa，第2壓力峰值平均衰減9.5%，衰減值為23.41 kPa，說明對于大氣團工況，增加壁面粗糙度會顯著降低兩個峰值壓力，且對第1壓力峰值影響更大。其原因是因為管壁粗糙度增大壁面剪切應力，使得在能量耗散過程中熱傳遞的比例所占比例不同。

4 結 論

(1)建立水流沖擊滯留氣團瞬變流的三維精細化模型。充分考慮了水氣兩相壓縮性、水-氣-管壁熱交換、管壁粗糙度等復雜因素進行三維建模，三維CFD模擬結果與實驗結果對比驗證了所建三維模型能準確地模擬瞬變壓力及水氣動態變化，可對水氣耦合瞬變流的進行精細深入研究。

(2)研究氣團長度、初始壓力對系統壓力峰值、壓力衰減(能量耗散)的影響。系統最大壓力隨氣團長度減小而增大，隨入口壓力增大而增大，且增值遠大于系統入口壓力增值。當初始氣團較長時，系統能量以熱量損失為主；當初始氣團較短時，熱量損失的比例降低，主要以摩阻損失為主。

(3)湍流模型是三維CFD建模的核心部分之一，影響管路系統的阻力、能量衰減的核心因素。對比發現，當氣團較長時，無論入口壓力大小均可以選擇RNGk-ε湍流模型；當氣團長度較短，入口壓力較小時，可以選擇Standardk-ε湍流模型，當入口壓力較大時，則可以選擇RNGk-ε湍流模型。

(4)管壁粗糙度對瞬態壓力的影響和氣團長度有關，總體趨勢保持一致，即隨著管壁粗糙度增加至0.5 mm時，系統壓力峰值逐漸降低，粗糙度增加越大，壓力衰減值越大。對于小氣團工況，壓力衰減主要作用于第二壓力峰值；對于大氣團工況，粗糙度會增加第一和第二壓力峰值的敏感性，且對第一壓力峰值的敏感性更高。粗糙度對壓力波動周期的影響可以忽略不計。