利用平面直角坐標系確定位置

陳金宇

生活中的難題無處不在，比如你想去某個地方卻找不到它在哪兒，想去電影院卻找不到自己的位置，想聽象棋解說卻聽不懂解說的走法等。這時候，我們所學的平面直角坐標系就派上用場了。我們一起來看兩道題。

題目1 如圖1，以小紅家為原點建立平面直角坐標系。小紅如果要從家出發去公園，應該如何走？請寫出公園坐標。同理，寫出圖中其余位置的坐標。

小紅的走法不唯一。她可以向右走兩個單位，再向上走兩個單位，也可以先向上走兩個單位，再向右走兩個單位。由此得出公園坐標為（2，2）。其他坐標以此類推。

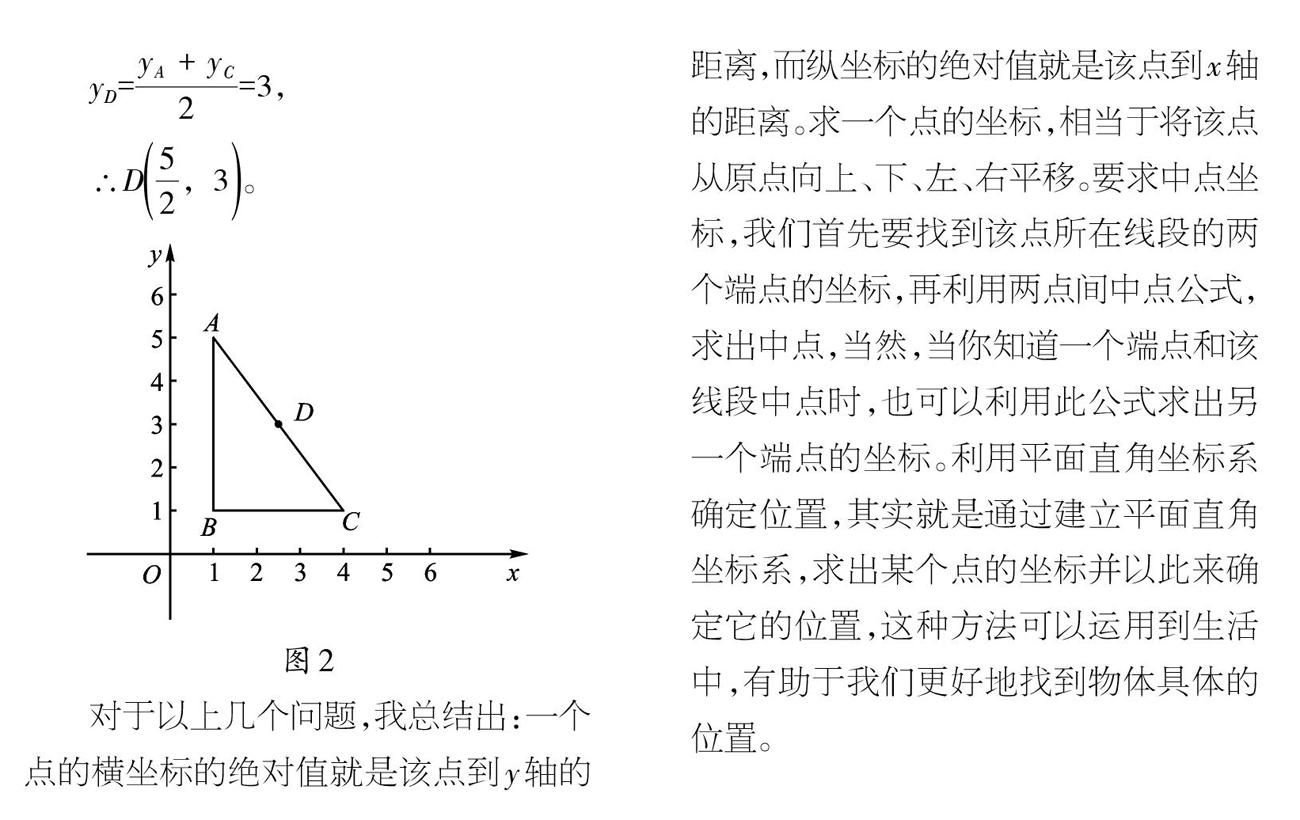
題目2 已知，等腰直角△ABC中，∠B=90°，點D為AC的中點，AB=4，BC=3，請在圖2的平面直角坐標系中標出點A、B、C、D的坐標。

由題目1的方法可求出除點D外的三點的坐標。在知道了點A、C的坐標之后，我們再根據兩點間中點公式可求點D的坐標。

對于以上幾個問題，我總結出：一個點的橫坐標的絕對值就是該點到y軸的距離，而縱坐標的絕對值就是該點到x軸的距離。求一個點的坐標，相當于將該點從原點向上、下、左、右平移。要求中點坐標，我們首先要找到該點所在線段的兩個端點的坐標，再利用兩點間中點公式，求出中點，當然，當你知道一個端點和該線段中點時，也可以利用此公式求出另一個端點的坐標。利用平面直角坐標系確定位置，其實就是通過建立平面直角坐標系，求出某個點的坐標并以此來確定它的位置，這種方法可以運用到生活中，有助于我們更好地找到物體具體的位置。

教師點評

確定平面內點的位置，通常過該點作x軸或者y軸的垂線，將問題轉化為求相關線段的長，再由點的位置求出點的坐標。運用數形結合思想和幾何知識是解答這類題的關鍵。

（指導教師：陸春霞）