基于改進變分貝葉斯濾波的SINS/DVL/LBL組合導航技術

趙俊波, 葛錫云, 成 月, 李 錦

基于改進變分貝葉斯濾波的SINS/DVL/LBL組合導航技術

趙俊波, 葛錫云, 成 月, 李 錦

(中國船舶科學研究中心, 江蘇 無錫, 214082)

為解決水下航行器捷聯慣性導航系統(SINS)與多普勒計程儀(DVL)、長基線(LBL)定位設備組合導航問題, 提出使用集中式濾波方案, 并建立了SINS/DVL/LBL組合導航模型。在組合導航過程中, 考慮到使用經典的卡爾曼濾波方法會存在由量測噪聲方差時變和野值干擾而導致濾波精度下降的問題, 通過將變分貝葉斯濾波與IGGⅢ權函數相結合, 提出了一種改進變分貝葉斯濾波方法。組合導航仿真結果表明: 文中濾波方法具有較強的自適應能力和抗野值能力, 其濾波精度優于經典的卡爾曼濾波方法和變分貝葉斯濾波方法。

水下航行器; 組合導航; 變分貝葉斯; IGGⅢ權函數; 野值

0 引言

水下高精度導航技術是水下航行器順利完成航行探測及作業任務的重要保障。近年來, 水下捷聯慣性導航系統(strapdown inertial navigation system, SINS)與多普勒計程儀(Doppler velocity log, DVL)組合導航技術日臻成熟, 并在水下航行器導航應用中發揮著重要作用[1-2]。在海洋探測及水下作業的市場需求牽引下, 水下長基線(long baseline, LBL)定位技術目前也取得了較大進展[3], 水下SINS/DVL組合導航與LBL相結合的方式逐漸成為研究熱點[4-5]。

卡爾曼濾波(Kalman filtering, KF)方法并不能處理模型噪聲方差時變的問題, 這將導致濾波精度下降甚至濾波發散[6]。在水下SINS/DVL/ LBL組合導航實際應用中, 由于DVL測速誤差方差會隨著航速或海況的變化而發生一定程度變化, 并且LBL定位誤差方差也會因偏離最佳作用區域或者信號遮擋出現一定程度的增大, 因此設備量測噪聲方差會發生變化。在上述情況下, 經典的KF方法將不再適用于SINS/DVL/ LBL組合導航。

解決組合導航量測噪聲方差時變問題通常采用自適應卡爾曼濾波方法, 這種自適應方法主要可分為2類[7]: 基于新息的自適應方法和基于多模型的自適應方法。變分貝葉斯濾波法[8-10]是近年來出現的一種基于新息的自適應濾波方法, Sarkka等[8]將變分貝葉斯估計和卡爾曼濾波方法相結合, 首次提出了變分貝葉斯自適應卡爾曼濾波(variational Bayesian adaptive Kalman filtering, VBAKF)方法。沈忱等[11]將變分貝葉斯濾波方法應用到SINS/GPS組合導航問題中, 消除了時變噪聲對卡爾曼濾波方法的影響; 郝燕玲等[12]針對SINS/GPS組合導航中量測噪聲統計特性不準確引起卡爾曼濾波精度下降的問題, 提出基于變分貝葉斯自適應無跡卡爾曼濾波的非線性融合方法; 徐健等[13]提出基于變分貝葉斯的平方根容積卡爾曼濾波算法, 并且用于水下無人航行器的航位推算與水下應答器的組合導航系統中。考慮到近年來變分貝葉斯濾波方法在處理組合導航噪聲自適應問題時發揮了很大的作用, 文中引入變分貝葉斯濾波方法來處理SINS/DVL/LBL組合導航量測噪聲方差時變的問題。

進一步考慮到DVL或LBL在使用過程中會不可避免地受到外界不確定因素干擾, 存在少數嚴重偏離真值的觀測野值, 若直接應用變分貝葉斯濾波進行SINS/DVL/LBL組合導航, 則會出現濾波精度下降的問題。為此, 文中在變分貝葉斯濾波算法的基礎上, 引入IGGⅢ權函數[14-15]對新息向量進行加權處理, 對變分貝葉斯濾波方法進行了算法改進, 提升了變分貝葉斯濾波方法的魯棒性, 有效地解決了上述濾波精度下降的問題。

1 SINS/DVL/LBL組合導航模型

對于多傳感器組合導航而言, 組合導航系統一般有集中式濾波和分散式濾波2種設計方法, 考慮到集中式濾波在實際工程中應用相對較多, 因此, 文中采取集中式濾波的方法實現SINS/DVL/LBL組合導航, 其基本原理如圖1所示。

圖1 SINS/DVL/LBL組合導航原理圖

組合導航系統一般以姿態誤差、速度誤差、位置誤差等誤差參數為系統狀態變量來設計濾波器。由于水下航行器深度參數可由深度計精確測量, 故這里忽略高度通道的狀態變量, 以降低濾波器維數, 進而減少計算復雜度。

在上述條件下, 水下SINS/DVL/LBL組合導航系統的狀態方程可寫為

水下SINS/DVL/LBL組合導航系統的量測方程為

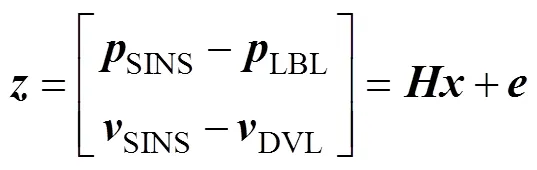
式中:為觀測量;SINS是SINS設備輸出的位置信息;LBL是LBL設備輸出的位置信息;SINS是SINS設備輸出的速度信息;DVL是DVL設備輸出的速度信息;為觀測噪聲向量;為觀測矩陣[5]。

2 改進變分貝葉斯濾波方法

2.1 變分貝葉斯濾波基本原理

變分貝葉斯濾波是一種自適應濾波方法, 是變分貝葉斯估計與卡爾曼濾波相結合的結果, 其關鍵點在于近似求解后驗概率密度的變分貝葉斯估計方法。

變分貝葉斯估計方法是在傳統遞推貝葉斯估計與期望最大化(expectation-maximum, EM)迭代估計算法的基礎上, 引入變分近似理論而提出的, 該方法將較難求解的貝葉斯估計的概率密度分解為易于求解的多個概率密度。

假設線性離線系統模型為

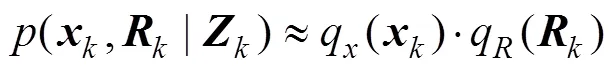
變分貝葉斯濾波算法可概括如下[7]。

1) 時間更新

2) 量測更新

2.2 改進變分貝葉斯濾波算法

在組合導航解算過程中, 為保證濾波精度, 要求當觀測數據不包含野值時, 濾波器能夠充分利用有效的新息; 當觀測數據中有少量野值時, 能夠克服其不良影響, 或者能將其影響控制在預先給定的界限內, 以確保濾波估計值盡可能接近系統的真實狀態。考慮到IGGⅢ方案是一種經典的抗差估計方法, 該方法按照IGGⅢ權函數將觀測數據按照質量劃分成了有效信息、可利用信息和有害信息3類, 在處理靜態測量平差及動態導航定位問題上取得了較好的效果[14-15]。為此, 引入IGGⅢ權函數來改進變分貝葉斯濾波算法, 進而抵抗野值的干擾。

設

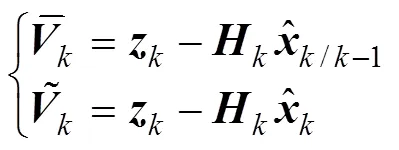
對于線性系統而言, 當系統模型誤差向量和觀測誤差向量均為零均值高斯白噪聲序列時, 新息向量也是零均值高斯白噪聲序列, 卡爾曼濾波此時為系統狀態最優估計。當觀測向量混入野值, 則觀測誤差向量不再服從高斯分布, 致使新息向量不再是標準的白噪聲序列, 從而導致卡爾曼濾波精度下降甚至發散。若將新息向量進行加權處理, 則可將新息序列進行白噪聲的近似化處理, 從而提高濾波精度。因此, 對新息的處理方法可表述為

文中的改進VBAKF算法可表述如下。

1) 時間更新

同2.1節中的時間更新, 具體可參見式(5)。

2) 量測更新

a. 循環初始化

b. 循環主體部分

c. 最終參數賦值

3 仿真驗證

為驗證文中提出的改進VBAKF算法的有效性, 對SINS/DVL/LBL組合導航系統進行1 h的MATLAB仿真。設置2組對比試驗, 分別與經典的KF方法以及VBAKF方法進行位置誤差和速度誤差對比。

為模擬水下巡航探測場景, 水下航行器以3 kn的巡航速度在水平面內按割草式循環軌跡作往復運動, 每航行1 200 s后作2次轉向運動且每次轉向90°, 然后開始反向航行。其中, 第1次通過左轉調頭, 第2次通過右轉調頭。水下航行器的航行軌跡如圖2所示, 仿真試驗以東北天3個方向建立局部導航坐標系, 并將軌跡初始點定義為坐標原點。水下航行器初始位置為經度120°、緯度25°、深度10 m、初始航向角90°、縱傾角0°、橫傾角0°, 初始速度、加速度、角速度和角加速度均為0。

圖2 航行軌跡圖

1) 自適應濾波性能

試驗假定設備DVL測速誤差標準差在1 000~ 1 500 s內為0.5 m/s, 其余時段為0.05 m/s; 設備LBL定位誤差標準差在2 500~ 3 000 s內為10 m, 其余時段為1 m。仿真結果如圖3和圖4所示。

圖3 量測噪聲方差時變情形下的位置誤差對比圖

從圖3和圖4可以看出, 在1 000~1 500 s內, DVL噪聲標準差增大到0.5 m/s, 經典的KF方法的濾波精度明顯下降, 速度誤差出現了較大波動, 最高可達0.3 m/s, 且定位精度同樣也受到了較大影響; 然而VBAKF方法和改進VBAKF方法的濾波精度幾乎不受影響。在2 500~3 000 s內, LBL噪聲標準差增大到10 m, 經典的KF方法對位置、速度的濾波精度同樣顯著下降, 定位誤差甚至增大到了5 m, 然而測量噪聲增大對VBAKF方法和改進VBAKF方法的濾波精度影響較小, 位置誤差基本上能控制在1 m以內。

圖4 量測噪聲方差時變情形下的速度誤差對比圖

由此可以看出, 當DVL或LBL量測噪聲方差增大時, 經典的KF方法的濾波精度明顯下降, VBAKF方法和改進VBAKF方法的濾波效果相當, 都能夠有效處理該問題, 實現自適應濾波, 提升濾波精度。

2) 抗野值干擾能力

試驗假定DVL和LBL的測量噪聲均為2種均值相同(零均值)、方差不同的高斯白噪聲的混合噪聲。具體而言, 若用表示測量噪聲, 則

式中:服從;服從, ; 以0.9的概率出現在量測值中, 以0.1的概率出現在量測值中。試驗中取DVL測量誤差標準差為0.05 m/s, 取LBL測量誤差標準差為1 m, 其仿真結果如圖5和圖6所示。

圖6 量測野值干擾情形下的速度誤差對比圖

由圖5和圖6可以看出, 當DVL和LBL量測值中存在野值干擾時, 經典KF方法的濾波精度最差, VBAKF方法有一定的抗干擾能力, 但濾波精度較低, 而改進VBAKF方法的濾波精度最高。由此可以看出, 改進VBAKF方法有較強的抗野值干擾能力, 其濾波精度高于KF方法和VBAKF方法。

4 結束語

針對水下SINS/DVL/LBL組合導航過程中, 使用經典的卡爾曼濾波方法可能會存在由量測噪聲方差時變和野值干擾而導致濾波精度下降的問題, 文中提出了一種改進變分貝葉斯濾波方法。該方法是一種基于新息的自適應濾波方法, 通過將變分貝葉斯濾波與IGGⅢ權函數相結合, 提升了變分貝葉斯濾波的魯棒性。最終通過Matlab仿真, 驗證了該方法在處理上述精度下降的問題上的有效性。

為考慮水下航行器偏離LBL最佳作用區域這一工況, 下一步研究會將LBL定位系統中各信標的測距信息納入觀測量, 探究引入信標測距信息觀測量對SINS/DVL/LBL組合導航濾波精度的改善效果。

[1] Leonard J J, Bahr A. Autonomous Underwater Vehicle Navigation[M]. Springer: Handbook of Ocean Engineering, 2016.

[2] 趙俊波, 葛錫云, 馮雪磊, 等. 水下SINS/DVL組合導航技術綜述[J]. 水下無人系統學報, 2018, 26(1): 2-9.Zhao Jun-bo, Ge Xi-yun, Feng Xue-lei, et al. A Review of Underwater SINS/DVL Integrated Navigation Technology[J]. Journal of Unmanned Undersea Systems, 2018, 26(1): 2-9.

[3] 孫大軍, 鄭翠娥, 張居成, 等. 水聲定位導航技術的發展與展望[J]. 中國科學院院刊, 2019, 34(3): 331-338.Sun Da-jun, Zheng Cui-e, Zhang Ju-cheng, et al. Development and Prospect for Underwater Acoustic Positioning and Navigation Technology[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(3): 331-338.

[4] 張濤, 陳立平, 石宏飛, 等. 基于SINS/DVL與LBL交互輔助的AUV水下定位系統[J]. 中國慣性技術學報, 2015, 23(6): 769-774.Zhang Tao, Chen Li-ping, Shi Hong-fei, et al. Underwater Positioning System Based on SINS/DVL and LBL Interactive Auxiliary for AUV[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 769-774.

[5] 李旻. 基于SINS/DVL與聲學定位系統的水下組合導航技術研究[J]. 艦船電子工程, 2018, 38(12): 60-64.Li Min. Study of Underwater Integrated Navigation Technology Based on SINS/DVL and Acoustic Positioning System[J]. Ship Electronic Engineering, 2018, 38(12): 60-64.

[6] 嚴恭敏, 翁浚. 捷聯慣導算法與組合導航原理[M]. 西安: 西北工業大學出版社, 2019.

[7] Mohamed A H, Schwarz K P. Adaptive Kalman Filtering for INS/GPS[J]. Journal of Geodesy, 1999, 73: 193-203.

[8] Sarkka S, Nummenmaa A. Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations [J]. IEEE Transactions on Automatic Control, 2009, 54(3): 596-600.

[9] Sarkka S, Hartikainen J. Non-linear Noise Adaptive Kalman Filtering via Variational Bayes[C]//2013 IEEE International Workshop on Machine Learning for Signal Processing (MLSP). Southampton, UK: IEEE, 2013.

[10] Huang Y L, Zhang Y G, Wu Z M, et al. A Novel Adaptive Kalman Filter with Inaccurate Process and Measurement Noise Covariance Matrices[J]. IEEE Transactions on Automatic Control, 2018, 63(2): 594-601.

[11] 沈忱, 徐定杰, 沈鋒, 等. GPS/INS組合導航的變分貝葉斯自適應卡爾曼濾波[J]. 哈爾濱工業大學學報, 2014, 46(5): 59-65. Shen Chen, Xu Ding-jie, Shen Feng, et al. Variational Bayesian Adaptive Kalman Filtering for GPS/INS Integrated Navigation[J]. Journal of Harbin Institute of Technology, 2014, 46(5): 59-65.

[12] 郝燕玲, 張召友. 基于VB-UKF的SINS/GPS自適應融合技術[J]. 華中科技大學學報: 自然科學版, 2012, 40(1): 54-57.Hao Yan-ling, Zhang Zhao-you. Adaptive Fusion Technology for SINS/GPS Based on VB-UKF[J]. Journal of Huazhong University of Science and Technology- Medical Sciences, 2012, 40(1): 54-57.

[13] 徐健, 宋曉萍, 張宏瀚, 等. 基于變分貝葉斯的DR/UTP組合導航濾波方法[J]. 儀器儀表學報, 2016, 37(12): 2743-2749.Xu Jian, Song Xiao-ping, Zhang Hong-han, et al. DR/UTP Integrated Navigation Based on Variational Bayes[J]. Chinese Journal of Scientific Instrument, 2016, 37(12): 2743-2749.

[14] 楊元喜. 自適應動態導航定位[M]. 第2版. 北京: 測繪出版社, 2017.

[15] 劉宸, 劉長建, 王賽, 等. 兩種新的IGGⅢ的改進方案[J]. 測繪通報, 2016(10): 54-57.Liu Chen, Liu Chang-jian, Wang Sai, et al. Two New Improvements of IGGⅢ Scheme [J]. Bulletin of Surveying and Mapping, 2016(10): 54-57.

SINS/DVL/LBL-integrated Navigation Technology Based on Improved Variational Bayesian Filtering

ZHAO Jun-bo, GE Xi-yun, CHENG Yue, LI Jin

(China Ship Scientific Research Center, Wuxi 214082, China)

To solve the integrated navigation problem of an undersea vehicle strapdown inertial navigation system (SINS), Doppler velocity log(DVL), and long baseline(LBL) location equipment, a centralized filtering scheme is proposed in this study and a SINS/DVL/LBL-integrated navigation model is established. During integrated navigation, using the classical Kalman filtering method leads to the problem in which the filtering accuracy is reduced due to time-varying measurement noise variance and the interference of outliers. Accordingly, an improved variational Bayesian filtering method is proposed by combining a variational Bayesian filter with an IGGIII weight function. Integrated navigation simulation is conducting using MATLAB software, and results show that the proposed filtering method has strong self-adaptive and anti-outlier abilities as well as a higher filtering accuracy than the classical Kalman filtering and variational Bayesian filtering methods.

undersea vehicle; integrated navigation; variational Bayesian; IGGⅢ weight function; outliers

TJ630; TP391.9

A

2096-3920(2021)01-0054-06

10.11993/j.issn.2096-3920.2021.01.008

趙俊波, 葛錫云, 成月, 等. 基于改進變分貝葉斯濾波的SINS/DVL/LBL組合導航技術[J]. 水下無人系統學報, 2021, 29(1): 54-59.

2020-04-20;

2020-05-23.

江蘇省自然科學基金項目(BK20180171); 海南省重大科技計劃項目(ZDKJ2019002).

趙俊波(1990-), 男, 碩士, 工程師, 主要研究方向為水下組合導航技術.

(責任編輯: 許 妍)