基于改進型ADRC的全驅動AUV建模與仿真

王 震, 王俊雄, 牛嘯辰, 蘇 偉

基于改進型ADRC的全驅動AUV建模與仿真

王 震, 王俊雄, 牛嘯辰, 蘇 偉

(上海交通大學 船舶海洋工程國家重點實驗室, 上海, 200240)

自主水下航行器(AUV)具有非線性、強耦合且易受外界干擾等特點。為進一步提高AUV的控制精度, 文中首先對六自由度全驅動AUV進行了建模, 并搭建了相應的比例-積分-微分(PID)控制器和自抗擾控制器(ADRC), 對比分析可知, 傳統ADRC待調整參數過多且跟蹤微分器(TD)環節速度較慢。針對此, 采用Asin函數對傳統ADRC的各環節進行了簡化, 改進了TD的結構, 并在相同仿真條件下對PID控制器及改進型ADRC控制器的控制效果進行了仿真。結果表明, 在對多自由度運動系統進行控制時, 改進型ADRC相較于PID的控制精度更高, 抗干擾能力也更強。

自主水下航行器; 自抗擾控制器; 比例-積分-微分控制; 路徑跟蹤

0 引言

近年來, 水下機器人被越來越廣泛的關注和應用。其中, 自主水下航行器(autonomous under- sea vehicle, AUV)因不需要人工干預就可以自行在海底作業, 無論在軍事領域(監視、偵察、檢查、排雷)還是民用領域(海底測繪、石油工業、漁業)都有著非常高的應用價值。由于AUV系統有著多變量、非線性及強耦合等特點, 實際工作中還會受到來自不同方向的水流、旋渦等因素干擾, 因此設計高抗干擾能力的AUV是其水下穩定工作的關鍵。

目前, 國內外學者多采用比例-積分-微分(pr- oportional integral derivative, PID)控制、滑模結構控制、模糊自適應控制及神經網絡控制等方法進行AUV動態控制研究, 其中PID控制器占據AUV控制的主導地位。但由于差分方法在提取微分信號時對噪聲十分敏感, 因此在很多場景下PID退化為PI控制, 通常控制器的響應速度慢且誤差較大[1]。此外, 在處理多自由度相互耦合的系統時, PID控制器往往力不從心, 難以實現較好的控制效果。自抗擾控制(active disturbance rej- ection control, ADRC)方法另辟蹊徑, 在控制多自由度問題時可以將其他通道對當前通道的干擾通過擴張狀態觀測器觀測出來, 在解決多自由度耦合問題上有著天然的優勢。

文中基于澳洲國立大學給出的Kambara水下機器人模型相關參數, 在Simulink下搭建了其六自由度(6 degree of freedom, 6-DOF)工作模型, 并采用反雙曲正弦函數構建了改進型ADRC控制器, 同時為進一步提高控制精度, 對傳統跟蹤微分器的結構進行了進一步優化; 接著對模型施加正弦擾動并通過螺旋線仿真試驗比較了改進型自抗擾、傳統PID 2種控制策略在有干擾情況下的控制效果。

1 控制對象建模

1.1 運動學建模

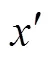
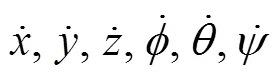
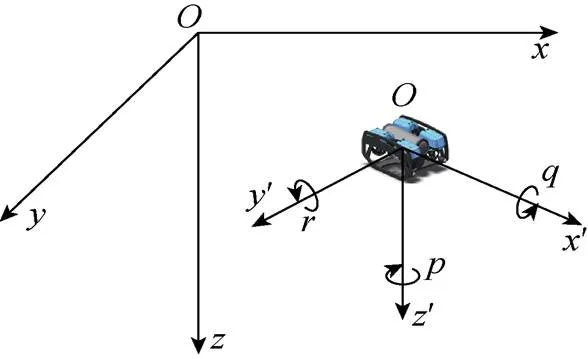
圖1 地球坐標系和載體坐標系

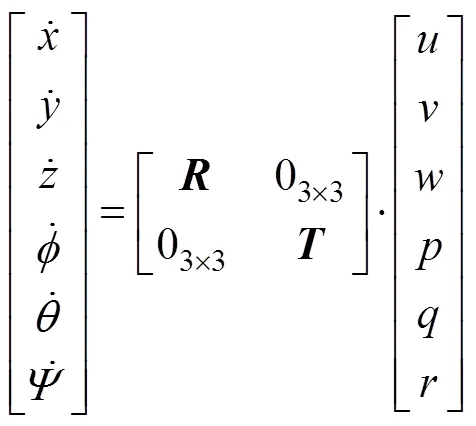
式中,、為轉移矩陣, 且

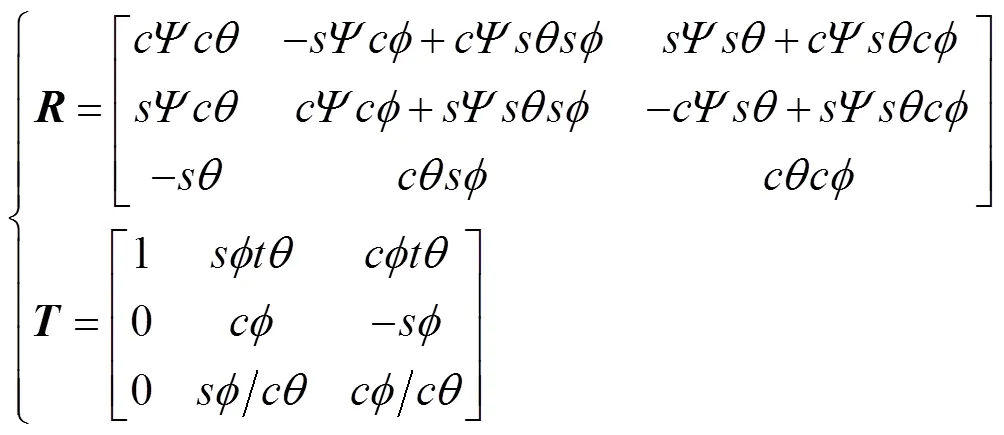
1.2 動力學建模

由于AUV在水中的運動是一個非常復雜的流固耦合問題, 為便于進一步研究, 首先對AUV的運動過程進行如下假設: 1) 假設AUV為剛體, 質量不隨時間變化; 2) 不考慮地球自轉對AUV運動的影響; 3) 模型所處流場為穩態流場, 周圍水流為靜止狀態。

根據非慣性坐標系下的牛頓運動定律, 得到AUV在載體坐標系下的運動方程

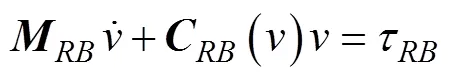
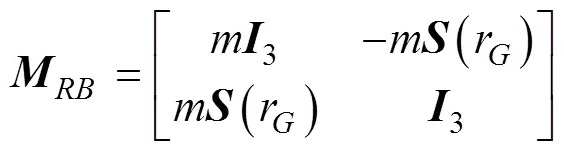
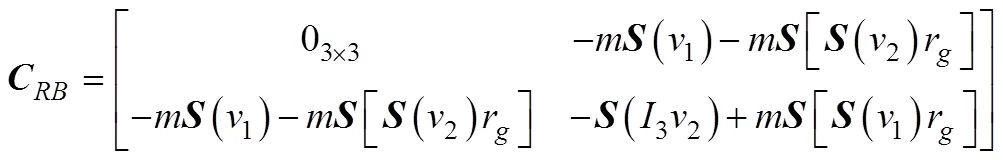
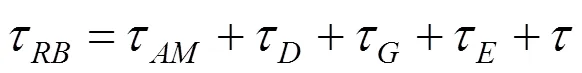
整理得AUV在理想狀態下矢量化動力學模型

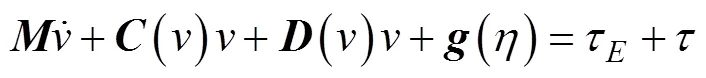
此外，神經細胞外葡萄糖濃度的增加將導致乙酰硫激酶活性降低，使Schwann細胞中脂肪過量累積，導致神經損傷。同時，葡萄糖由醛糖還原酶催化生成更多的山梨醇和果糖，產生較高的滲透壓、細胞水腫和神經纖維的變性和壞死，從而促進LA的形成。

1.3 仿真模型搭建

通過對模型進行動力學和運動學分析, 可以著手搭建控制對象的Simulink仿真模型, 仿真過程中使用模型參數如表1所示。

表1 AUV相關參數

2 控制系統設計

2.1 ADRC控制技術概述

非線性ADRC控制系統包含3個主要部分: 擴張狀態觀測器(extended state observer, ESO); 跟蹤微分器(tracking differentiator, TD)和安排過渡過程; 非線性狀態誤差反饋控制律(nonlinear states error feedback control laws, NLSEF)。圖2是一種典型的2階非線性ADRC控制系統。

2.2 ADRC控制器設計

由于ADRC控制器存在的天然解耦優勢, 可以先針對單DOF 2階系統設計相應的ADRC控制器, 之后再將其拓展到6-DOF系統。

假設被控對象狀態方程為

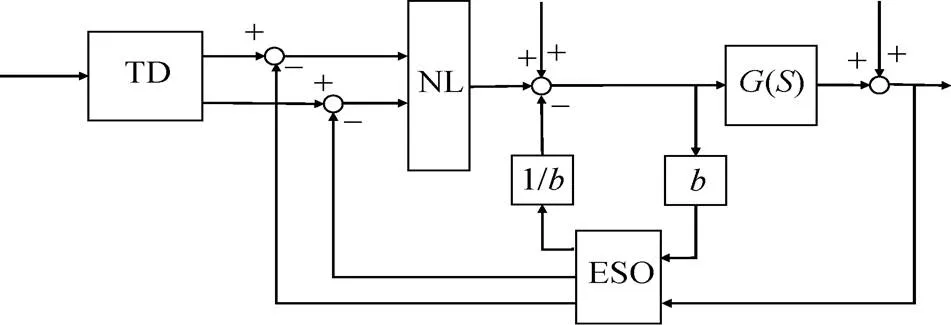
圖2 ADRC控制系統結構示意圖

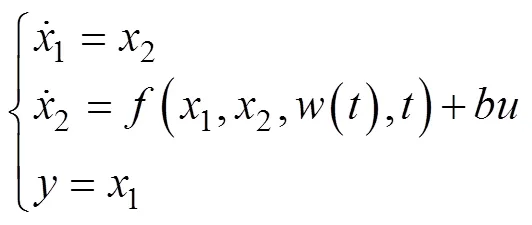
2.2.1 擴張狀態觀測器(ESO)

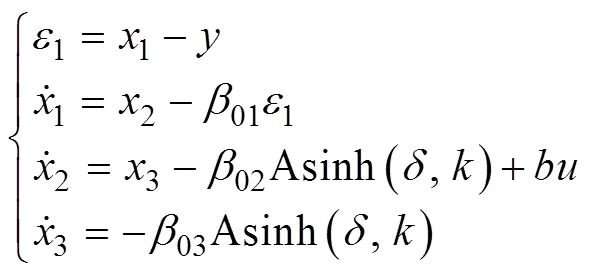
通過將信號進行解構可得相應的跟蹤信號1及跟蹤信號對應的微分信號2。傳統TD架構為

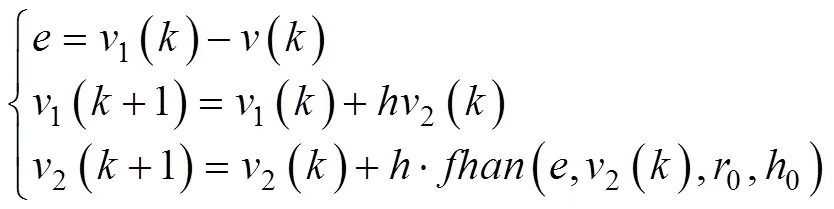
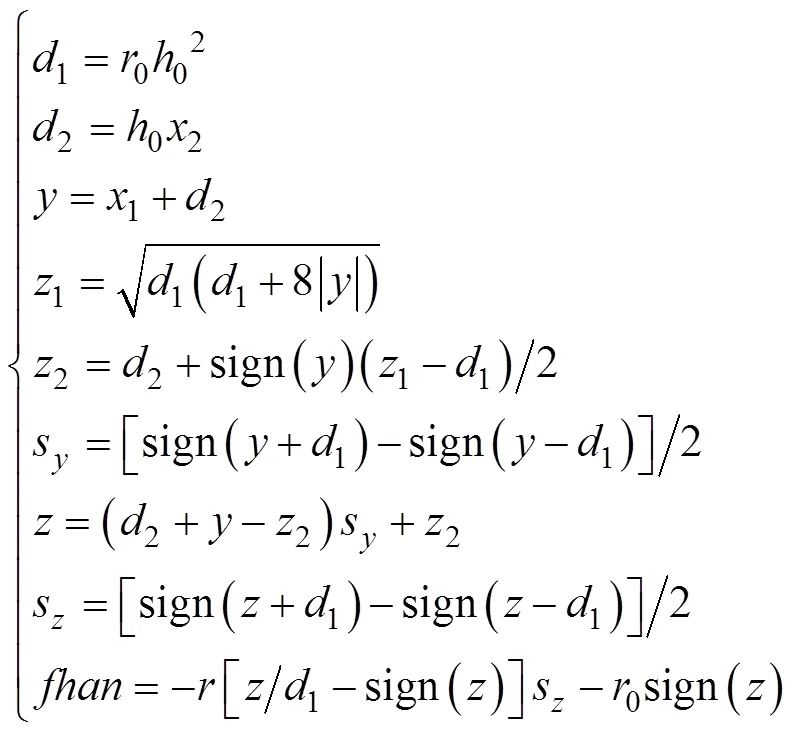
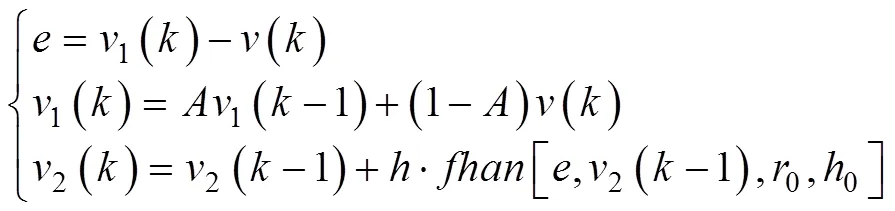
式中,為濾波參數。

2.2.3 非線性狀態誤差反饋控制律(NLSEF)

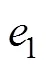
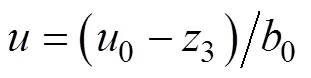
2.3 控制模型搭建

將搭建完成的控制器和控制對象聯立, 可得多自由度全驅動AUV的ADRC控制系統模型, 見圖3。

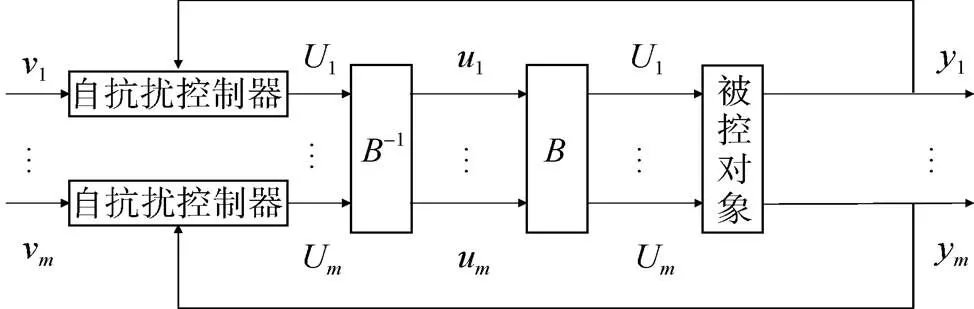
圖3 多自由度全驅動AUV控制系統

2.4 參數整定及控制器優化

非線性ADRC控制器的一般形式有多達12個控制參數, 即使是簡化后的模型也有8個控制參數。由于控制參數眾多, 且調參難度較高, 不少學者就該問題展開了一系列的研究。目前常用的參數整定方法有經驗法、人工智能法和基于時間尺度方法等。

通過動態參數整定, 將TD、ESO和NLSEF看作彼此較為獨立的3部分, 先對TD和ESO進行參數整定, 在取得較為滿意的效果之后, 結合NLSEF對ADRC控制器進行整體的參數整定。

為了簡化ESO的整定過程, 將涉及到的相關參數取為

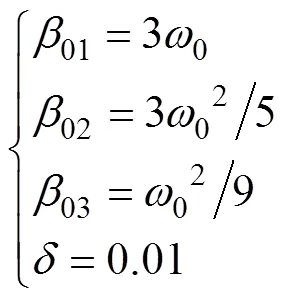
3 控制對象建模

為了驗證改進型ADRC控制器的抗擾能力及控制效果, 首先在單DOF情況下分別對PID控制器及ADRC控制器進行了在有正弦干擾情況下的位置階躍仿真。仿真時間為1 000步, 階躍信號在第100 s給出, 階躍信號峰值為50, 正弦干擾信號的表達式為

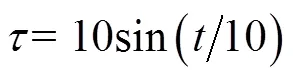
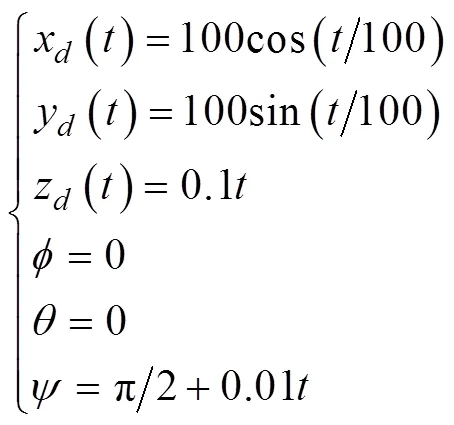
外加擾動

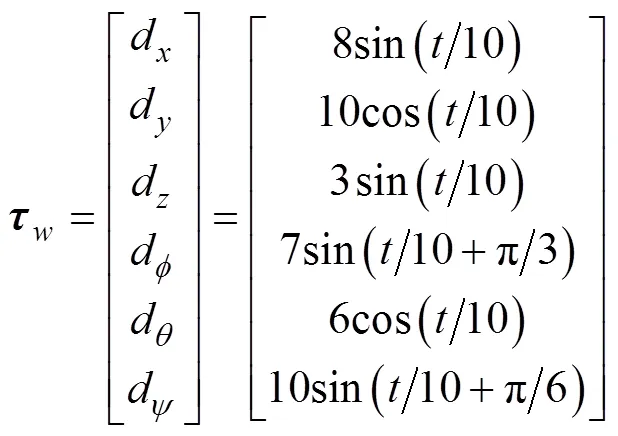
首先, 為驗證ADRC控制器的抗干擾能力, 在相同的仿真條件及控制參數下, 搭建ADRC控制系統與PID控制系統, 在進行動態參數整定后, 對2套控制系統同時施加正弦干擾信號, 并給出對y軸坐標的位置階躍跟蹤仿真結果, 如圖4所示。在施加正弦外界干擾的情況下, ADRC控制器與PID控制系統對單DOF階躍信號的跟蹤能力基本相同, 然而在達到目標位置后, PID系統存在較為嚴重的隨擾動而抖動的現象, 偏移幅度最大為0.69, 而ADRC系統雖然也受到正弦干擾的影響, 但其最大偏移幅度僅為0.18, 遠小于PID的最大偏移值, 這說明ADRC在位置階躍響應時的抗干擾能力更強。

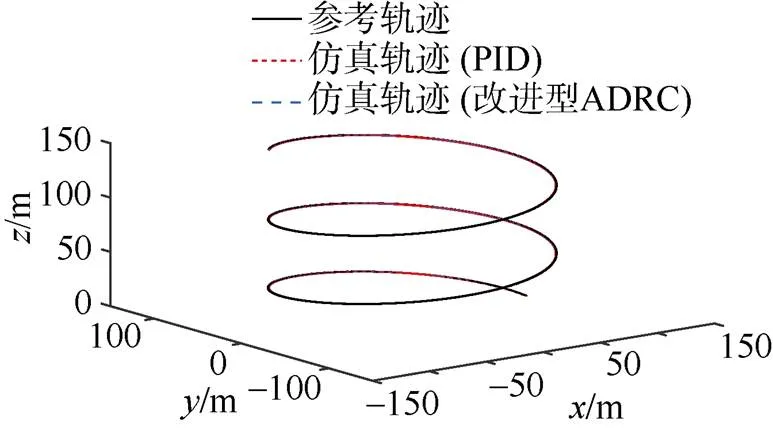
圖5 螺旋線跟蹤仿真曲線

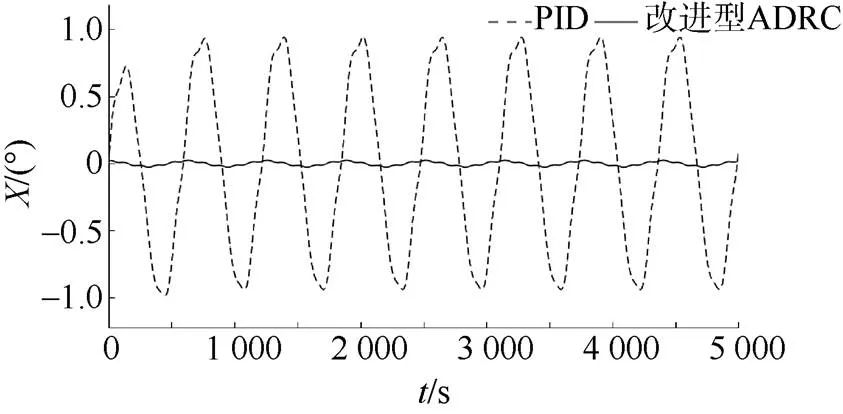
圖6 X方向跟蹤誤差曲線

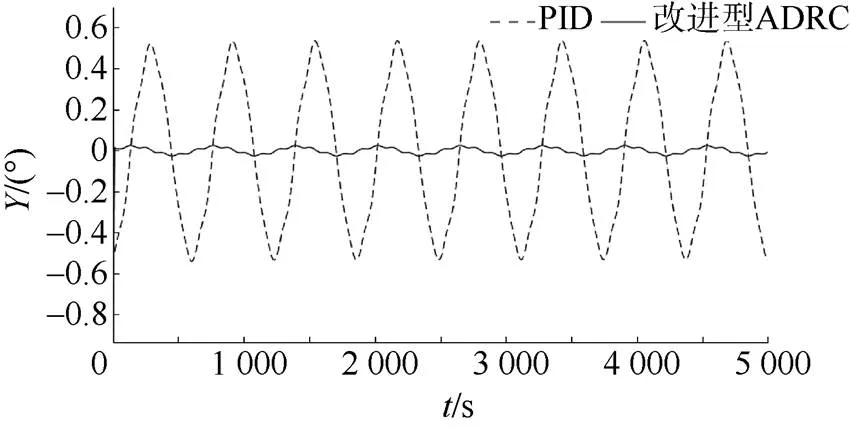
圖7 Y方向跟蹤誤差曲線

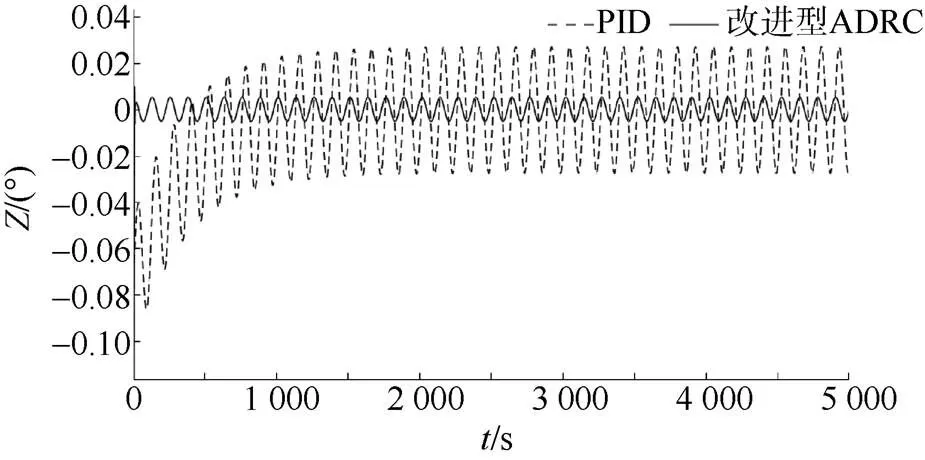
圖8 Z方向跟蹤誤差曲線

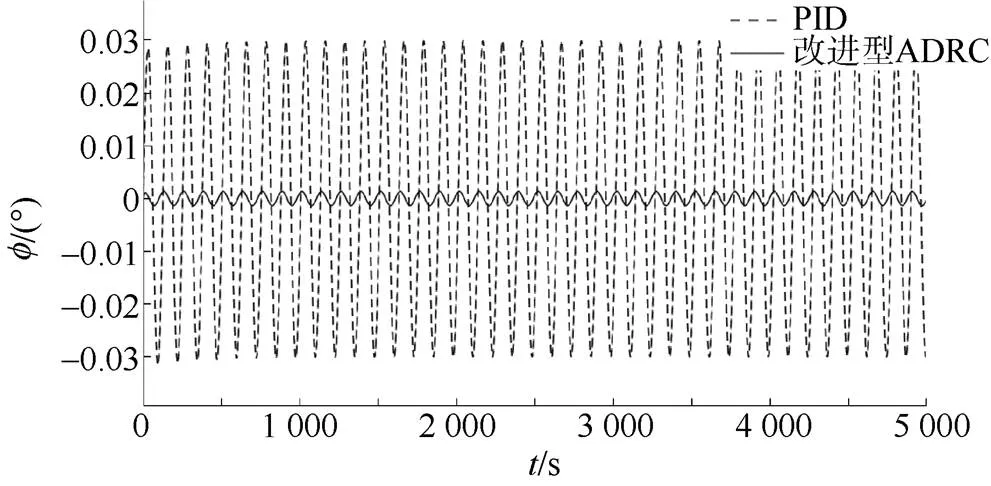
圖9 ?方向跟蹤誤差曲線

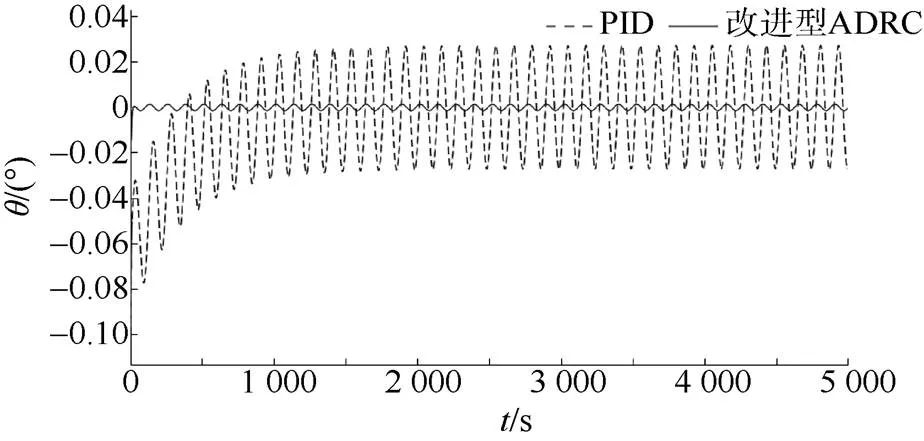
圖10 q方向跟蹤誤差曲線

圖11 ψ方向跟蹤誤差曲線

4 結束語

文中提出了一種基于反雙曲正弦函數及改進型TD搭建的ADRC控制系統, 該控制系統有著比傳統ADRC更少的待調參數, 且能夠實現對AUV的高精度控制。基于該改進型ADRC控制器的相關仿真試驗表明, 相比于傳統的PID控制器, 其更加適用于多因素耦合的水下機器人系統, 可實現更高精度的控制, 控制過程也更加穩定, 在進行螺旋線仿真時的跟蹤精度也更高。針對改進型ADRC系統結構的進一步分析論證, 將是未來的研究方向。

[1] 韓京清. 自抗擾控制器及其應用[J]. 控制與決策, 1998, 13(1): 19-23.Han Jing-qing. Auto-disturbances-rejection Controller and It’s Applications[J]. Control and Decision, 1998, 13(1): 19-23.

[2] 韓京清. 從PID技術到“自抗擾控制”技術[J]. 控制工程, 2002, 9(3): 13-18.Han Jing-qing. From?PID?Technique?to?Active?Disturb- ances?Rejection?Control?Technique[J]. Control Enginee- ring of China, 2002, 9(3): 13-18.

[3] 周濤. 永磁同步電機調速系統的自抗擾控制[J]. 光學精密工程, 2016, 24(3): 582-589.Zhou Tao. Active Disturbance Rejection Control of Speed Governing System for PMSM[J]. Optics and Precision Engineering, 2016, 24(3): 582-589.

[4] 高劍. 無人水下航行器自適應非線性控制技術[M]. 西安: 西北工業大學出版社, 2016: 15-63.

[5] 趙志良. 自抗擾控制設計與理論分析[M]. 北京: 科學出版社, 2019: 180-231.

[6] Habib C L, Zhu Q D. Path Following Control of Fully-actuated Autonomous Underwater Vehicle in Presence of Fast-varying Disturbances[J]. Applied Ocean Research, 2019, 86: 40-46.

[7] Casta?eda L A, Luviano-Juárez A, Ochoa-Ortega G, et al. Tracking Control of Uncertain Time Delay Systems: An ADRC Approach[J]. Control Engineering Practice, 2018, 78(9): 97-104.

[8] 萬磊, 張英浩, 孫玉山, 等. 欠驅動智能水下機器人的自抗擾路徑跟蹤控制[J]. 上海交通大學學報, 2014, 48 (12): 1727-1731.Wan Lei, Zhang Ying-hao, Sun Yu-shan, et al. ADRC Path- Following Control of Underactuated AUVs[J]. Journal of Shanghai Jiaotong University, 2014, 48(12): 1727-1731.

[9] 胡文華, 曹仁贏. 四軸飛行器串級ADRC軌跡跟蹤控制[J]. 武漢科技大學學報, 2019, 42(4): 299-304.Hu Wen-hua, Cao Ren-ying. Trajectory Tracking Control for Quadrotor Based on Cascaded ADRC[J]. Journal of Wuhan University of Science and Technology(Natural Science Edition), 2019, 42(4): 299-304.

[10] Horacio C E, John C R, Sergio A, et al. Rejection of Varying-frequency Periodic Load Disturbances in Wind-turb- ines through Active Disturbance Rejection-based Control [J]. Renewable Energy, 2019, 141: 217-235.

[11] Plaskonka J. The Path Following Control of a Unicycle Based on the Chained form of a Kinematic Model Derived with Respect to the Serret-Frenet Frame[C]//Methods and Models in Automation and Robotics(MMAR). 2012 17th International Conference. Miedzyzdrojie: MMAR, 2012.

[12] Fu C F, Tan W. Tuning of Linear ADRC with Known Plant Information[J]. ISA Transactions, 2016, 65: 384-393.

[13] 張勇, 陳增強, 張興會, 等. 基于自抗擾的四旋翼無人機動態面姿態控制[J]. 吉林大學學報(工學版), 2019, 49 (2): 562-569.Zhang Yong, Chen Zeng-qiang, Zhang Xing-hui, et al. Dynamic Surface Attitude Control of Quad-rotor UAV ba- sed on ADRC[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(2): 562-569.

[14] 高強, 劉俊杰, 劉文杰. 四旋翼飛行器姿態的自抗擾控制研究[J]. 計算機仿真, 2016,33(12):38-41.Gao Qiang, Liu Jun-jie, Liu Wen-jie. Attitude Regulation of Quadrotor UAV Via ADRC Methodology[J]. Computer Simulation, 2016, 33(12): 38-41.

Modeling and Simulation of Fully Actuated AUV Based on Modified ADRC

WANG Zhen, WANG Jun-xiong, NIU Xiao-chen, SU Wei

(State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

Autonomous undersea vehicles(AUVs) are nonlinear, strongly coupled, and vulnerable to external disturbances. To improve the control accuracy of AUVs, a 6-degree-of-freedom fully actuated AUV is modeled, and a proportional integral derivative(PID) controller and auto disturbance rejection controller(ADRC) are built. A comparative analysis reveals that the traditional ADRC has too many parameters to adjust, and the tracking speed of each link of the tracking differentiator(TD) is slow. Therefore, the Asin function is used to simplify each link of the traditional ADRC, and the structure of the TD is improved to solve the problem of slow tracking speed. The control effect of the PID and modified ADRC is simulated under the same simulation conditions. Simulation results show that the modified ADRC has higher control accuracy and stronger anti-disturbance ability than PID when the motion of a multi-freedom system is controlled.

autonomous undersea vehicle(AUV); auto disturbance rejection controller(ADRC); proportional integral derivative(PID) control; path tracking

TJ630.33; TP13

A

2096-3920(2021)01-0048-06

10.11993/j.issn.2096-3920.2021.01.007

王震, 王俊雄, 牛嘯辰, 等. 基于改進型ADRC的全驅動AUV建模與仿真[J]. 水下無人系統學報, 2020, 28(6): 48-53.

2019-12-04;

2020-04-04.

王 震(1996-), 男, 碩士, 主要研究方向為水下機器人路徑跟蹤.

(責任編輯: 楊力軍)