基于RBF 代理模型的袋式除塵器清灰性能優化設計

劉麗冰，沈玉鎮，熊桂龍，張 磊

（1.河北工業大學機械工程學院，天津300130；2.南昌大學資源環境與化工學院，江西 南昌 330031；3.河北工業大學人工智能與數據科學學院，天津300130）

1 引言

脈沖噴吹袋式除塵器擁有除塵效率高、使用壽命長等優勢，是目前解決工業粉塵排放的關鍵設備[1]。脈沖清灰是袋式除塵器過濾再生循環過程，其性能優劣直接關系到除塵器能否長期保持穩定運行。清灰性能受多種因素影響，影響因素與清灰性能之間存在高度非線性隱式關系。

國內外學者通過模型試驗和數值模擬的方式對脈沖清灰的影響參數進行了大量的研究。模型試驗方面，文獻[2]用直徑0.13m，長度1.5m 的濾袋進行了試驗研究，發現濾袋內外壓差沿著濾袋長度的方向一直增加，濾袋底部的內外壓差是最大的。文獻[3]應用1：1 實物模型建立了一套清灰過程測量系統，對脈沖清灰的影響因素進行了細致的研究。隨著計算機技術的發展，數值模擬被廣泛應用在清灰性能的研究中，文獻[4]以單條濾袋為脈沖清灰仿真研究對象，研究了濾袋長度、噴嘴直徑、噴吹距離和噴吹壓力對清灰效果的影響；文獻[5]通過數值模擬研究發現濾袋長度、噴嘴直徑和文丘里管喉管直徑對清灰性能影響較大；文獻[6]采用響應面法，研究了包括噴吹高度等四個清灰相關參數對清灰效果的影響，發現噴吹高度影響很小。由此可見，對袋式除塵器清灰性能的研究多使用數值模擬方法且均著重考慮單個參數對清灰性能的影響。

對于多參數耦合的復雜非線性脈沖清灰系統，若直接使用數值模擬方法來進行多參數耦合優化效率極低，難以得出精確的優化結果，應用代理模型技術可以有效解決這個難題。基于代理模型的優化是根據統計學原理首先進行試驗設計獲取樣本點和設計空間，通過得到的數據建立優化目標和設計變量之間的代理模型，進而在模型的基礎上采用優化算法進行優化獲取最優解。代理模型在優化領域得到了深入的發展和廣泛的應用，文獻[7]綜述了工程設計優化中的代理模型并總結了不同代理模型的工程應用實例；文獻[8]在飛機旋翼的優化設計中應用代理模型技術；文獻[9]將代理模型應用在客機的優化設計中；除了航空航天領域，代理模型技術還廣泛用于解決水下機器人[10]、塑件翹曲[11]、汽車吸能盒[12]等各個領域的非線性、多參數耦合優化難題。將代理模型技術引入袋式除塵器產品技術研發領域用于解決清灰性能優化問題，是一種針對復雜優化難題實現高效解決的新思路。

在常用的代理模型中RBF 代理模型具有很好的處理強非線性問題的能力，是一種計算效率較高且結構簡單的代理模型。因此對袋式除塵器清灰性能優化設計中，采用RBF 代理模型和遺傳算法相結合的方法，以數值模擬為基礎獲取優化目標響應值，應用拉丁超立方試驗設計控制清灰參數的設計空間，根據得到的試驗數據建立清灰參數與響應值之間的徑向基函數代理模型，并在此基礎上采用遺傳算法進行優化得到最優的清灰參數組合。

2 RBF 代理模型

2.1 拉丁超立方試驗設計

代理模型的構造基礎是樣本點的選取，代理模型的精度很大程度取決于樣本點選取的好壞。若想選取少量具有代表性的能反映設計空間特性的樣本點，就要進行試驗設計，合理的試驗設計能夠影響后續結果的準確性。常用的試驗設計方法主要分為基于邊界和基于空間填充兩大類。基于邊界的試驗設計方法包括全因子法、Box-Behnken 設計等。基于空間填充的試驗設計方法主要包括拉丁超立方設計、均勻設計等。基于邊界的試驗設計方法隨著設計空間維數的增加，所需樣本點個數成指數倍增長。在復雜的實際工程問題中過多的試驗次數顯然是無法接受的，因此采用基于空間填充的試驗設計方法對袋式除塵器清灰系統性能進行優化設計。

拉丁超立方試驗設計方法在各種代理模型中廣泛應用，該方法本質是控制取樣點的位置，避免在小范圍內重復取點，確保產生的樣本點能夠代表整個設計空間。拉丁超立方試驗設計的主要優點是設計空間的全部信息均已涵蓋、所取樣本點均勻分布在設計空間、樣本點個數無要求可以自定義且不需要考慮設計樣本的維數。

2.2 RBF 代理模型

徑向基函數模型是以徑向函數為基函數，以樣本點和預測點之間歐氏距離為自變量，通過線性疊加構造出來的模型。它的基本形式，如式（1）所示。

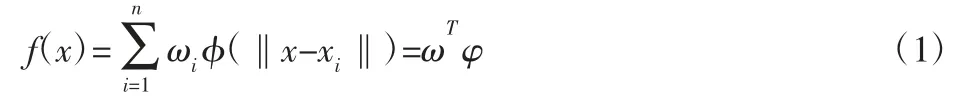
其中權重系數ω（x）=（ω1，…，ωn）T，基函數φ=（φ（‖x-x1‖），…，φ（‖x-xn‖））T。

用式（1）作預測模型，應滿足如下插值條件：

式中：f（xi）—預測值；yi—精確值；n—樣本點數量。于是有：

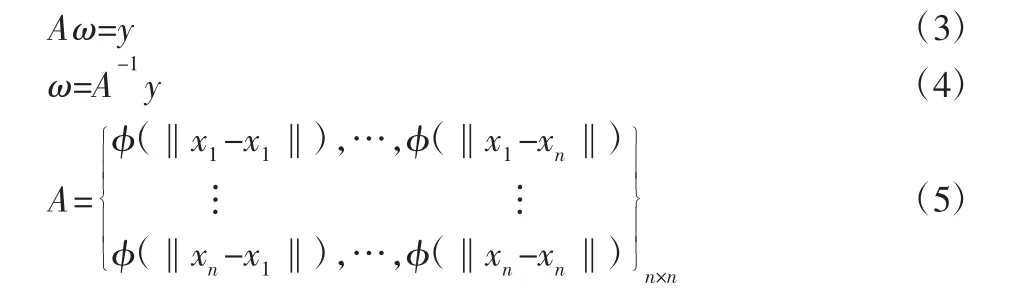
其中φ 代表徑向函數，常用的徑向函數包括：多二次函數、高斯函數、三次函數等。采用不同的徑向函數會使徑向基函數代理模型特性不同，本研究中使用多二次函數，模型具有全局估計的特點，表達式，如式（6）所示。

式中：r—預測點和任意樣本點之間的歐氏距離；c—正實數。

3 基于RBF 模型的清灰性能優化設計

3.1 數值模擬模型

以單條濾袋作為脈沖清灰仿真研究對象，將噴吹管、噴嘴、引流區域及濾袋內外部空間作為計算區域，計算對象的幾何模型，如圖1 所示。邊界條件主要設置如下：噴吹管入口采用壓力入口邊界條件，考慮到脈沖閥開關過程中壓縮空氣的壓力變化，入口邊界條件采用UDF 自定義函數；濾袋邊界條件設置為多孔跳躍介質。脈沖清灰過程中，清灰氣流屬于高度非線性的復雜流動狀態，遵循著動量守恒、能量守恒和質量守恒定律。在CFD 計算過程中采用可壓縮、非穩態的數學模型和Realization k-ε 雙方程模型。

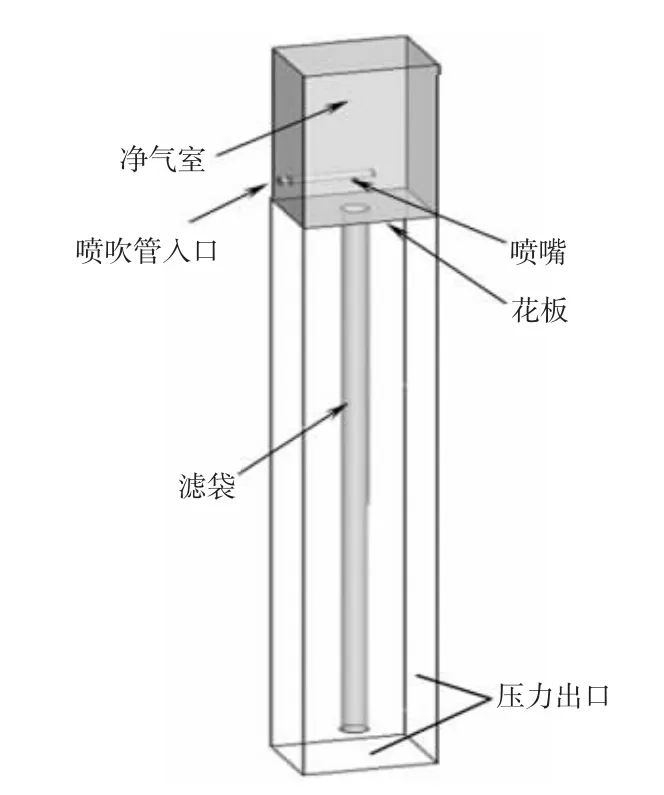
圖1 計算模型圖Fig.1 Geometric Model

3.2 清灰性能優化策略

在數值模擬的基礎上，基于RBF 代理模型進行清灰性能優化，具體的優化流程如下：

（1）分析優化問題，明確優化目標，選取對清灰性能影響較大的參數作為設計變量并確定設計空間。

（2）采用拉丁超立方試驗設計抽取樣本點，通過數值模擬計算出樣本點處的真實響應值。

（3）利用抽取的樣本點和所對應的真實響應構建RBF 代理模型，得到優化目標和清灰參數之間的關系。

（4）用均方根誤差法檢驗RBF 代理模型的精度。若滿足要求進入下一步驟，否則增加樣本點個數，優化試驗設計，直到精度滿足要求為止。

（5）采用遺傳算法尋取全局最優解，找到最優清灰參數組合。

袋式除塵器在清灰過程中，壓縮空氣從噴口在瞬間噴出，誘導數倍的二次空氣高速射入濾袋，對濾袋壁面產生沖擊作用，使得粉塵剝落，達到清灰的目的。在以往的研究中，研究者多將噴吹后濾袋側壁上獲得的壓力峰值作為衡量清灰性能好壞的主要指標。由于濾袋底部側壁壓力峰值較小，當濾袋底部滿足清灰要求時，則濾袋整體清灰性能得以保證。因此，本研究中選定距袋底1m 處的側壁壓力峰值F 來表征清灰性能，即優化目標選定為F。

對清灰性能有影響的設計參數有許多，如噴吹壓力，濾袋長度、噴嘴直徑、噴嘴個數、濾料特性等等。本研究中選取噴吹壓力P、濾袋長度L、濾袋直徑D、噴嘴直徑d 這四個可變且對清灰性能影響較大的參數作為設計變量，設計區間，如表1 所示。

確定優化目標及設計變量后，優化問題可以表述為：

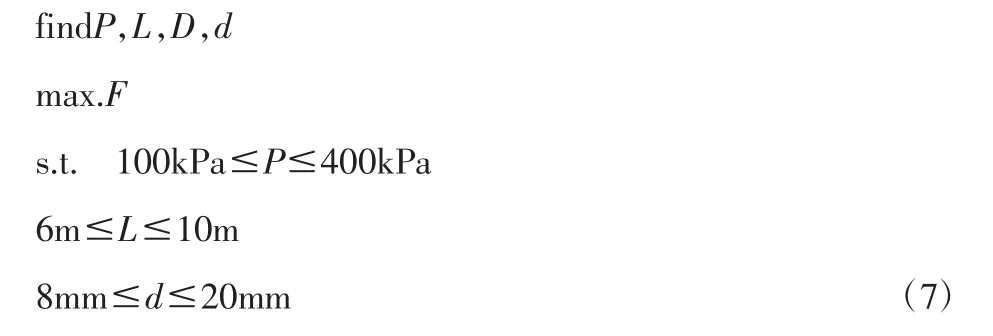
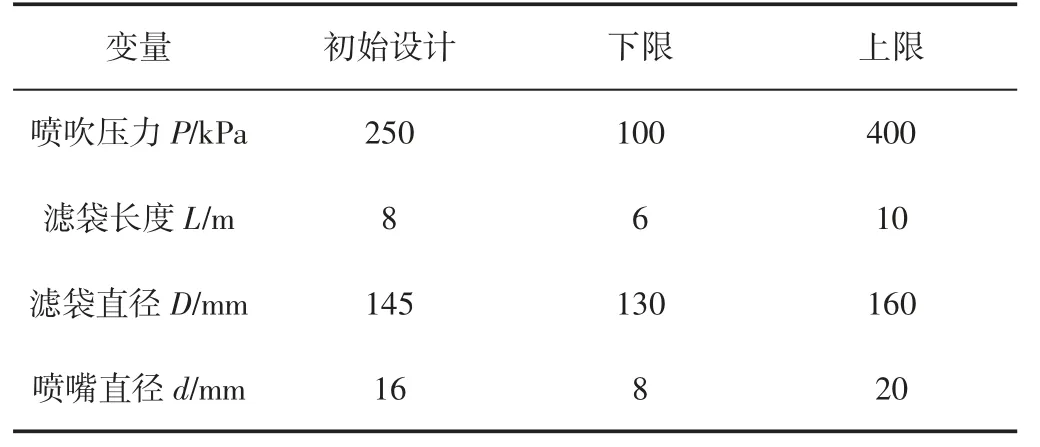
表1 變量設計區間及初始值Tab.1 Design Variable Space and Initial Size

采用拉丁超立方設計選取70 組樣本點數據，并通過數值模擬得到對應樣本點的響應值。其中70 組樣本點包括模型的擬合和模型的檢驗兩部分，RBF 模型的擬合運用前60 組數據，而RBF 模型的檢驗運用后10 組數據。拉丁超立方抽樣點及試驗結果，如表2 所示。

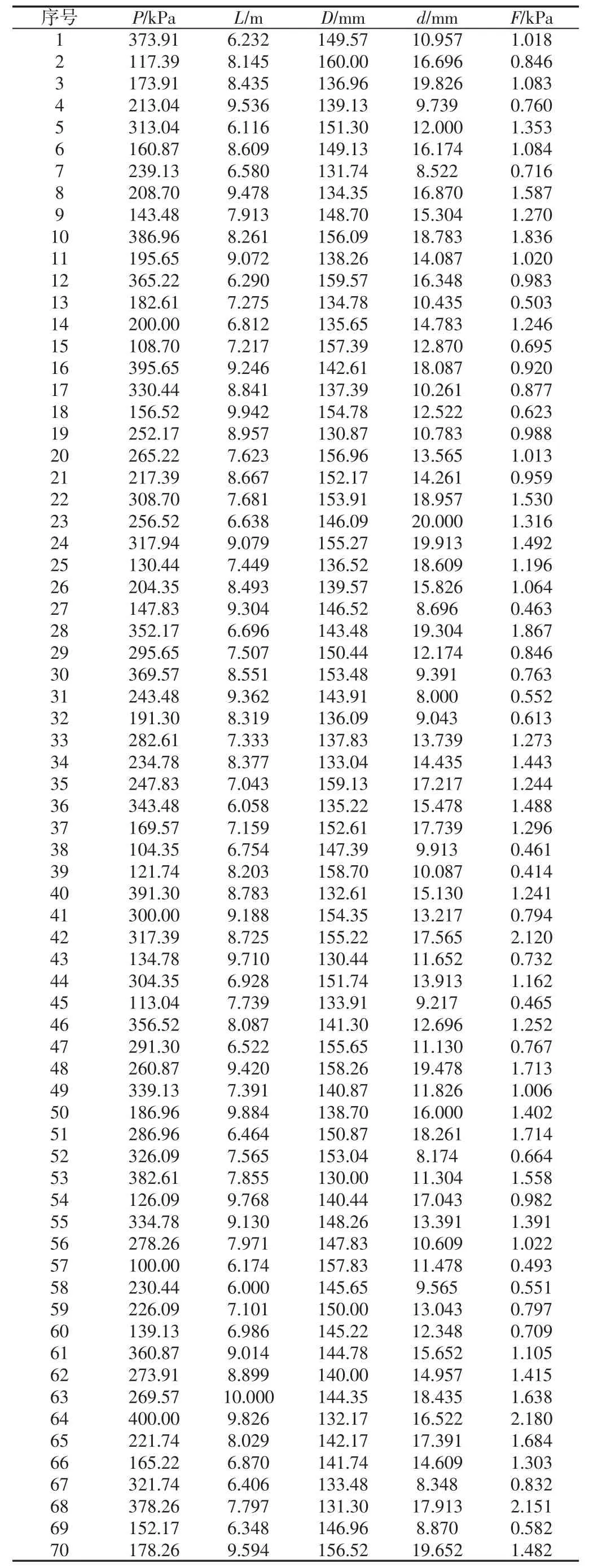
表2 拉丁超立方抽樣點及試驗結果Tab.2 Latin Hypercube Sampling Date and Experimental Result

4 清灰性能優化策略的實現

4.1 RBF 模型建立及精度檢驗

將清灰性能的關鍵參數噴吹壓力、濾袋長度、濾袋直徑、噴嘴直徑作為代理模型的設計變量，距袋底1m 處側壁壓力峰值作為代理模型輸出變量，以拉丁超立方設計得到的前60 組數據作為訓練樣本來構建RBF 代理模型。以表2 中后10 組數據作為檢測樣本檢測RBF 代理模型的精度，本研究選用均方根誤差法（RMSE）對RBF 模型進行精度檢驗。均方根誤差法的定義，如式（8）所示。

式中：nt—測試樣本點數量；yi—真實響應值；—代理模型的預測值，RMSE 的值越小說明代理模型的精度越高。十組測試樣本點的真實響應值和代理模型預測值結果，如表3 所示。

由表3 可見仿真值和預測值最大相對誤差為4.47%，表明模型的預測精度很好。計算得到RBF 模型的RMSE 值為0.024，接近于0，表明模型精度很高，可以代替數值模擬做計算。

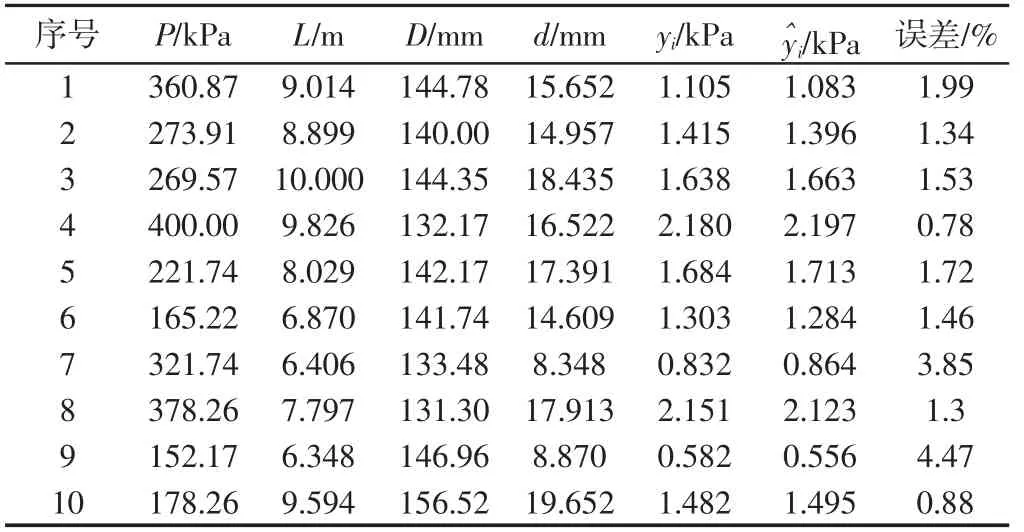
表3 RBF 模型精度檢驗Tab.3 RBF Model Accuracy Testing

4.2 遺傳算法尋優

遺傳算法（Genetic Algorithm，GA）由美國的Holland 教授于1975 年首先提出，是一種隨機全局搜索和優化方法，特別適合解決復雜和非線性問題。它本質是一種能夠進行全局搜索的并行、高效方法，優點是不依賴于梯度信息，不容易陷入局部最優。RBF代理模型能夠較好的擬合清灰參數和優化目標的關系，為尋找最優清灰參數組合，以各個清灰參數的取值范圍作為約束條件，以距袋底1 m 處側壁壓力峰值為優化目標，利用遺傳算法進行全局尋優。RBF 代理模型作為遺傳算法適應度函數的相反數，遺傳算法的種群規模數設置為M=50、終止代數T=100、交叉概率Pc=0.8、變異概率Pm=0.2。優化目標迭代過程，如圖2 所示。

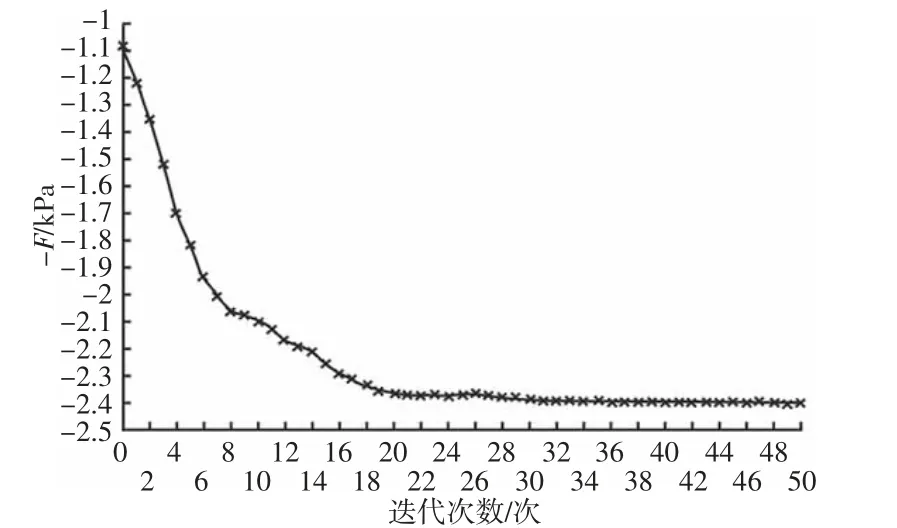
圖2 優化目標迭代過程Fig.2 Iterative Process of Optimizing Target

4.3 優化結果

遺傳算法優化得到的優化目標最優解為2.405 kPa；得到清灰參數最優組合為：噴吹壓力P=347.83 kPa、濾袋長度L=9.652 m、濾袋直徑D=143.04 mm、噴嘴直徑d=19.13 mm；將優化后的參數進行建模及仿真計算來驗證基于RBF 代理模型優化結果的正確性，得到數值模擬結果為2.294 kPa，與基于RBF 代理模型的優化結果相比，相對誤差為4.6%，說明基于RBF 代理模型的優化結果可靠。對清灰參數優化前后的數值模擬結果進行比較，其中清灰參數及數值模擬優化結果，如表4 所示。優化后的距袋底1m處的側壁壓力峰值比初始值提升了1.195kPa，說明清灰性能得到了明顯的提升，表明基于RBF 代理模型的優化方法適用于解決袋式除塵器清灰性能優化問題。

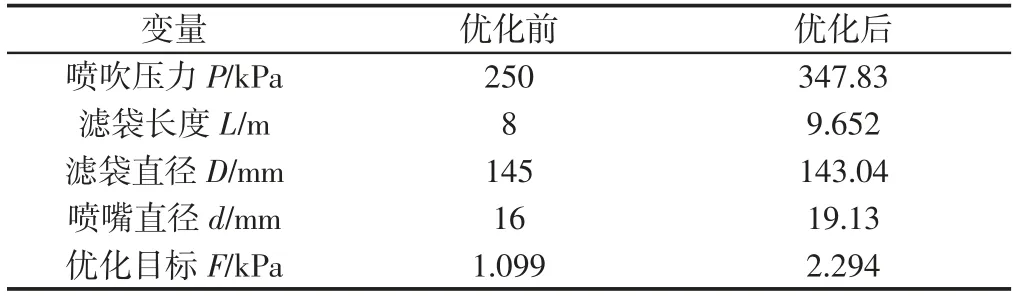
表4 數值模擬結果比較Tab.4 Comparison of Numerical Simulation Results

5 結論

（1）以噴吹壓力、濾袋長度，濾袋直徑、噴嘴直徑為設計變量，以距濾袋底部1 m 處側壁壓力峰值為優化目標，基于RBF 代理模型建立了具有較高精度的設計變量與優化目標間的近似函數關系，能替代耗時的數值模擬，節省計算資源，實現高效優化。（2）將RBF 代理模型和遺傳算法相結合，運用遺傳算法進行全局尋優，得到了全局最優解，確定了最佳的清灰參數組合。該方法簡單，易于實現多參數優化。（3）優化前后的對比結果顯示，優化后的距袋底1m 處的側壁壓力峰值最優解為2.294kPa，比初始值提升了1.195kPa，實現了對清灰性能的優化，為清灰性能優化設計提供了一種新的方法和思路。