“六招”輔助線解決全等三角形證明問題研究

龔惠芳

摘要：幾何圖形具有很強的抽象性，有些題目很難通過直觀觀察就能得到答案，人們在日常生活中遇到困難會尋求幫助，那么學習也是一樣的，通過直觀觀察找不到答案，那就試著做一些輔助的條件，來尋求題目的正確答案，給有些題目繪制出適當的輔助線往往就會有柳暗花明的感覺，一些看似很難找不到出路的幾何題目，通過繪制合適的輔助線便會很容易找到題目的答案，由此輔助線在初中平面幾何中也得到了初中幾何老師的青睞，數學老師在講解幾何難題時常常也會借助輔助線來找到答案。

關鍵詞：輔助線;全等三角;證明問題

引言：

初中幾何知識學習經常會用三角形全等的知識點來解決問題，這就要求初中學生應該熟練掌握三角形全等的知識，在學生對三角形全等性質進行學習的時候，有些題目根據條件和圖形就可以證明兩個三角形全等，但是大多數題目是需要借助輔助線來轉化已知條件，將復雜的題目簡單化才能找到答案，根據多年教學經驗，老師們也總結了很多添加輔助線的方法，以下主要對“六招”輔助線解決全等三角形證明問題研究做主要論述。

一、全等三角形的判定

通俗講全等三角形就是兩個三角形對應的邊和對應的角都應該相等。而判定三角形全等的主要方法有：SSS（三邊對應相等是全等）、SAS（兩邊及其夾角對應相等是全等）、AAS（兩角及其一角的對邊對應相等是全等）、ASA（兩角及其夾邊對應相等是全等）。

二、“六招”輔助線解決全等三角形證明問題研究

（一）圖形分割，公共邊來解圍

連接兩點線段，借助輔助線將一個四邊形劃分為兩個全等三角形。根據全等三角形的定義特征，證明兩個角相等。

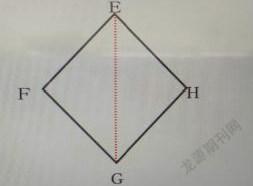
例：如圖，在四邊形EFGH中，已知EF=EH，GF=GH，求證∠F=∠H。

解析：在四邊形EFGH中沒有三角形，通過連接EG，將四邊形劃分為兩個三角形△EFG和△EHG，由于已知EF=EH，GF=GH，再加公共邊EG=EG，根據SSS（三條邊對應相等），得出△EFG和△EHG是全等三角形。據此可以得出∠F=∠H。

（二）連接兩點，同側公共邊來解圍

借助輔助線連接兩點線段，將所求角所在的三角形轉化到有共享邊的全等三角形中。根據全等三角形的定義特征，證明兩個角相等。

例：如下圖，已知EG與FH相較于O點，EF=HG，EG=FH，證明∠E=∠H。

解析：根據圖示可知，圖中雖然有兩個三角形，但是根據題意很難求證兩個角相等，但是將F點和G點相連，FG就是△EFG和△HGF的共享邊，根據SSS（邊邊邊相等）判定方法就能證明△EFG和△HGF是全等三角形，再根據全等三角形的定義就能證明∠E=∠H。

（三）延長線段，公共角來解圍

借助輔助線延長題目畫出的已知線段，通過構造公共角，求證兩個三角形全等，再根據全等三角形的定義特征，證明兩個角相等。

例：如下圖已知FH=GI，FG⊥于HF于F點，GI⊥于HI于I點，證明，FG=IH.

解析：在圖中分別含有線段FG和線段HI的三角形有好幾個，但是根據已知條件，我們很難求出兩條線段FG和IH相等，這時候我們將線段FG和線段IH分別延長相交與E點，則在△EGI和△EFH中∠E=∠E，∠EFH=∠EIG，FH=GI，則根據全等三角形的判定方法AAS（兩角及其一角的對邊對應相等的三角形是全等三角形），可以得知△EGI和△EFH是全等三角形，再根據全等三角形的定義就能證明EG=EH，EF=EI，又因為FG=EG-EF，IH=EH-EI，據此就可以推理出FG=IH.

（四）延長高線，角度轉移來解圍

當高與某角的平分線垂直，多采用借助輔助線延長垂直線段，進行所求角度的轉移。

例：在△EFH中，已知FI是∠EFH的平分線，EO⊥FI，證明∠FEG=∠GEH+∠EHG。

解析：通過直面觀察三個角好像沒什么關系，但是考慮到三角形內角以及平角的定理，我們可以將EO這條垂直線延長與△EFH的底邊FH相較于G點，那么如圖可構成△EFO和△GFO，在△EFO和△GFO中有個共用邊FO，∠FOE=∠FOG，∠EFO=∠GFO，那么根據全等三角形判定方法ASA（兩角及其夾邊對應相等的三角形是全等三角形），可得△EFO和△GFO是全等三角形，所以∠FEG=∠FGE，然而∠FGE=∠GEH+∠EHG，依次可以推理出∠FEG=∠GEH+∠EHG。

（五）加倍延長中線，倍長中線法

在日常解題中，遇到中線要借助輔助線對中線加倍延長，構造對等三角形。例：如下圖，在△EFH中，EO為邊FH上的中線，EF=EH=5，解答EO長的

值范圍。

解析：要想求得EO的取值范圍，就需要把與EO有關的線段轉化到同一個三角形中，然后根據三角形的三邊長度之間的定律求出EO的取值范圍，如圖首先把中線EO延長一倍，延長終點為G，連接FG，構成兩個三角形△FOG和△EOH，由已知條件及延長方法，根據全等三角形判定方法SAS（兩邊及其夾角對應相等的三角形是全等三角形），可得△FOG和△GOH是全等三角形，那么就把要求解的EO取值范圍轉移到了△FOG中，又因EO=OG，據此在△EFG中根據三角形三條邊的關系可以求出EO的取值范圍。

（六）平分線上圖形翻折，構造對等三角形

在角平分線的題目中，若需求解線段之間關系，往往是借助輔助線在三角形中構建對等三角形，將所求問題進行轉換。

例：圖中EH為△EGJ的中線，已知∠GHF=∠FHO，∠JHP=∠PHO，要求證明GF+PJ>FP。

解題分析：根具題意，無法直接找到三者之間的關系，往往需要借助輔助線構建全等三角形，將所求問題中的線段GF轉化為線段FO，將所求問題中的線段PJ轉化為線段PO，這樣就會將所求問題轉化到一個三角形中，再根據三角形三條邊之間的關系求解。

結語：

在初中平面幾何中輔助線具有增加條件，或將已有條件轉化到熟悉的幾何定理或性質上，起到了簡化題目的作用。這就要求教學老師要將輔助線的用法潛移默化地融入到數學題目講解之中，讓學生熟練掌握平面幾何中輔助線的應用方法與技能，養成擅于運用輔助線的良好習慣，并給以后立體幾何的學習打下堅持的基礎。

參考文獻：

[1]常海偉.三角形問題解答思路與途徑[J].數理化學習（初中版），2017，（8）.29-30.