ARIMA模型在丙型肝炎月發病數預測中的應用

劉雙，柳曉琳

(1.錦州醫科大學公共衛生學院，遼寧 錦州 121000；2.遼寧省朝陽市第二醫院，遼寧 朝陽 122000)

丙型病毒性肝炎(簡稱丙肝)，是由丙型病毒性肝炎病毒引起的一種傳染性疾病，血液途徑、性途徑、母嬰途徑為其擴散的主要方式[1]。世界衛生組織在2017年的報告中估計，全球丙肝感染率為1.0%，約有7100萬人為慢性丙肝感染病例，而中國2006年丙肝血清流行病學調查結果顯示，丙肝感染率0.43%，由此推算，中國丙肝感染者約為560萬。目前人群中尚沒有有效預防接種的生物制品進行注射，丙肝的防治已成為嚴重的公共衛生問題[2]。基于統計分析和數學模型等方法對丙肝疫情發展規律進行預測，是丙肝疫情的控制、預防以及衛生決策過程中不可或缺的科學依據。ARIMA模型是最基本應用最廣泛的模型之一[3]，它用相應的數學模型描述一組依賴于時間的隨機變量相互之間所具有的自相關性，以表征預測對象發展的延續性并從時序的過去值與現在值預測其未來值[4]。

本研究運用ARIMA模型對朝陽市2009年1月至2020年12月丙肝月發病數進行時間序列發展趨勢的研究，預測2021年朝陽市丙肝發病數，旨在為今后衛生行政部門傳染病防治和衛生應急工作部署提供參考依據。

1 資料與方法

1.1 一般資料

根據“中國疾病預防控制信息系統”中的“傳染病報告信息管理系統”，于2009年1月至2020年12月期間，收集朝陽市丙肝月發病數據。考慮到人口基數較大，最終本次研究以疾病的發病數代替了發病率進行分析預測。

1.2 方法

1.2.1 ARIMA建模步驟

應用SPSS 26.0軟件中ARIMA模型進行數據處理與分析。ARIMA模型建模過程包括4個階段：(1)數據平穩化處理：將2009年1月1日至2020年12月31日，丙肝月發病數的數據分為兩部分：2009年1月1日至2019年12月31日，丙肝月發病數作為訓練集構建時間序列模型，2018年1月1日至2018年12月31日，2020年1月1日至2020年12月31日，丙肝月發病數的數據作為驗證集評價模型預測效能，繪制丙肝月發病數時序圖判斷序列的特征及平穩性，對非平穩的原始序列采用差分的方法以達到序列平穩化，采用單位根(ADF)檢驗驗證序列平穩性；(2)模型的識別和定階：根據平穩序列自相關系數圖(ACF)、偏自相關系數圖(PACF)進行初步識別和定階，估計p、q、P、Q取值，在ARIMA模型中，P和Q的取值一般在0、1、2中選擇[5]，通過不同的取值構建多個模型；(3)模型參數估計和模型診斷：采用非線性最小二乘法對模型的參數進行估計，對參數進行t檢驗，殘差序列進行白噪聲Ljung-Box檢驗，根據貝葉斯信息準則(BIC)最小為標準綜合判定最優模型；(4)模型預測效果評價：采用平均絕對百分比誤差(MAPE)和均方根誤差(RMSE)[7-8]評價預測模型。平均絕對百分比誤差主要用來反映真實值與預測值之間差異的大小，計算公式：∑[|實際值-預測值|×100 /實際值] /樣本量。均方根誤差通常用于比較真實值與預測值之間的誤差，真實值和預測值之間的誤差越大，均方根誤差越大，計算方法：預測值與真實值差值的平方和與樣本量的比值的平方根。

1.3 統計學方法

采用Excel 2007及SPSS 26.0軟件對2009年1月至2020年12月的朝陽市丙肝月報告發病數進行錄入及整理，建立ARIMA時間序列模型預測2021年1月至2021年12月朝陽市丙肝發病趨勢。

2 結 果

2.1 數據平穩化處理

構建朝陽市2009年1月至2019年12月丙肝月發病數原始時間序列圖并進行趨勢分解，見表1、圖1，顯示該序列為非平穩時間序列，丙肝歷年發病數呈現明顯的上升趨勢(χ2=187.780，P<0.001)并具有明顯季節性效應，在2018年發病數達到峰值，之后稍作回落，每年的發病數在3月達到高峰。

對數據進行一階差分以及一階季節性差分，使序列基本平穩化，長期趨勢及季節波動基本消除，見圖2，采用單位根(ADF)平穩性檢驗P<0.001，證明序列處于平穩狀態。

2.2 模型識別和定階

根據原始時間序列特征分析，原始數據是以S=12為周期的季節性時間序列，經過一階差分以及一階季節性差分后，序列平穩化，可初步確定模型的參數d=D=1，因此初步確定模型的基本形式為：ARIMA(p，1，q)(P，1，Q)12，繪制數據預處理后平穩序列的ACF圖和PACF圖，時間序列的自相關系數在1階之后趨于平穩，偏自相關系數在2階之后趨于平穩，見圖3～4。初步判定p=1和q=2。根據相關經驗，p(P)與q(Q)取值超過2階的情況很少，所以P、Q取為0，1，2進行篩選。考慮模型的擬合效果、最小信息準則和殘差序列等有關指標綜合進行評價。

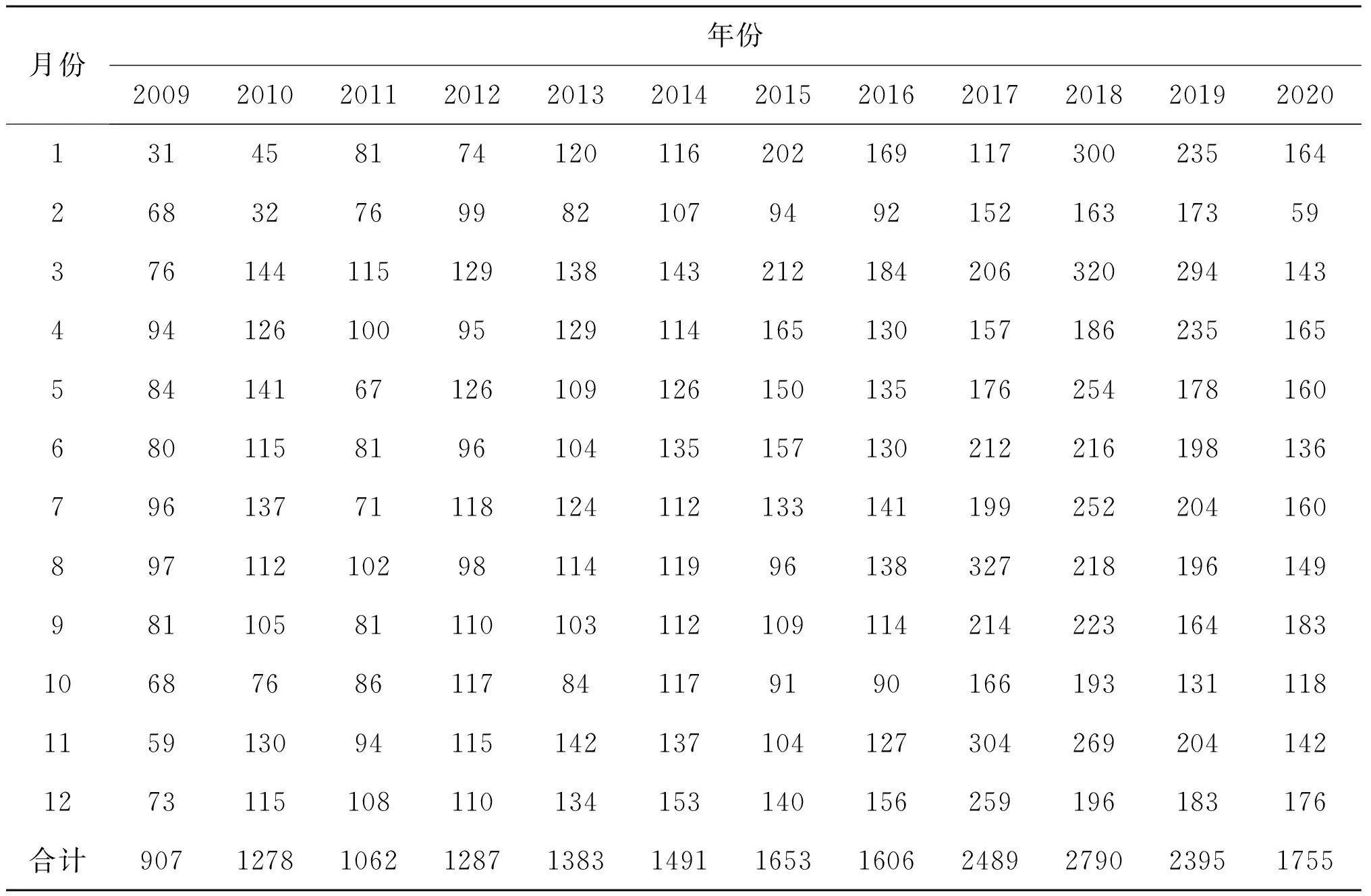
表1 2009—2020年朝陽市丙肝月發病數

圖1 2009—2019年朝陽市丙肝月發病數原始時序圖

圖2 2009—2019年朝陽市丙肝原始時間序列一階差分及一階季節性差分后平穩時序圖

圖3 丙肝月發病數預處理后的時間序列自相關圖

2.3 模型參數估計和模型診斷

利用SPSS 26.0軟件建立丙肝預測備選模型，通過白噪聲Ljung-Box檢驗和模型系數的t檢驗要求，剔除不滿足要求的模型，得到四個備選模型信息，見表2。根據BIC值最小原則選擇最優模型，其中BIC最小模型為ARIMA(1，1，2)(1，1，2)12，并通過白噪聲檢驗，P>0.05，可認為各個時滯的殘差之間無相關性，殘差序列為白噪聲序列。對確定的最優模型的參數進行t檢驗，P<0.05，模型參數檢驗具有統計學意義；模型的擬合優度值平穩R2=0.656，認為模型擬合良好，BIC=7.350，結果最小，認為模型較優，見表3。

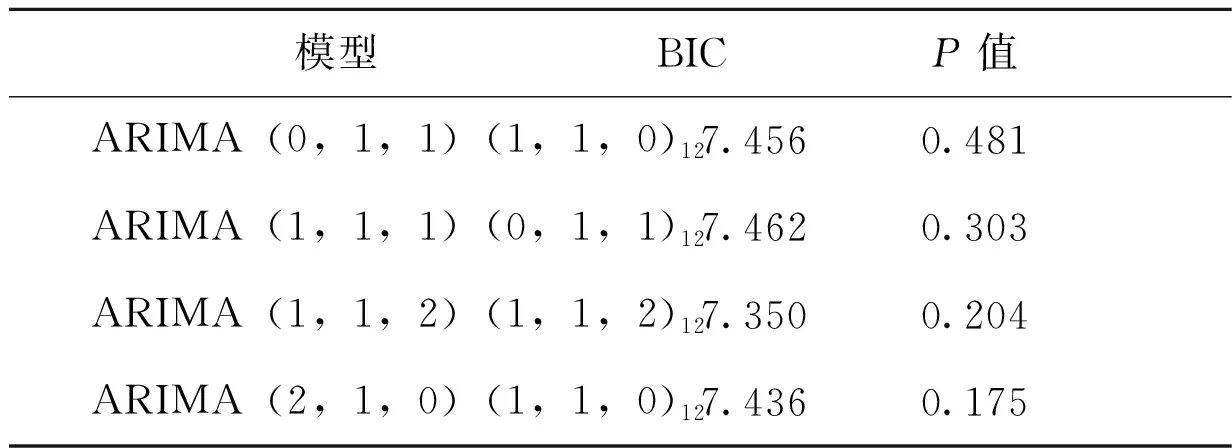
表2 丙肝備選模型信息表

表3 模型參數估計與檢驗結果情況

2.4 模型預測及效果評價

運用篩選出的最優模型ARIMA(1，1，2)(1，1，2)12對朝陽市2020年的數據進行擬合預測，采用MAPE及RMSE評價模型預測效能，根據預測值及真實值得MAPE=9.41%，RMSE=15.17，見表4、圖5。再次運用2009年1月至2017年12月丙肝月發病數據對2018年丙肝的月發病數進行擬合預測，由真實值及預測值得MAPE=6.40%，RMSE=15.92，見表5、圖5。運用朝陽市丙肝月發病數兩次對最優模型的預測效果進行評價，MAPE<10%，RMSE<20，認為模型的精度較高，預測效果良好。

運用模型ARIMA(1，1，2)(1，1，2)12對2021年12個月的數據進行擬合預測，結果顯示2021年朝陽市丙肝整體的發病數有所上升，合計發病1885例，較2020年丙肝發病數1775例上升了6.20%，預計在未來3月為丙肝的高發月，見表6。

圖5 2009—2020年朝陽市丙肝月發病數模型擬合結果

表4 2020年朝陽市丙肝月發病數預測值與真實值比較

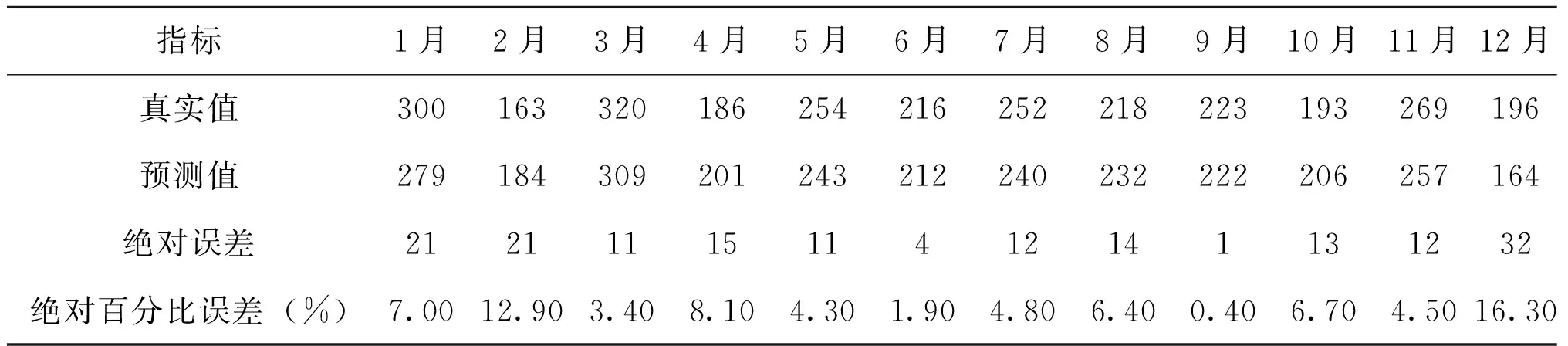
表5 2018年朝陽市丙肝月發病數預測值與真實值比較

表6 2021年朝陽市丙肝月發病數預測值

3 討 論

ARIMA模型近年來被廣泛應用于傳染病的短期預測[9]，它不僅綜合考慮了疾病可能存在的長期趨勢、季節效應、周期性及隨機波動，而且對模型的參數采用量化的方式進行檢驗并評價模型優劣，具有建模過程簡單、經濟、實用，短期預測精度高等特點[8]。丙型肝炎病毒多損害患者肝臟，因具有較強的傳染性、較廣的涉及范圍、較高的發病率和較為復雜的傳播方式，是我國常見的一種對人群威脅較大的血源及性傳播傳染病[9]。2019年新型冠狀病毒肺炎疫情席卷全球，仍是當前和未來一段時間最為嚴重的“國際關注的公共衛生事件”和“重大危機”，故本文分別對2018年、2020年月發病數進行了回代性預測，得到丙肝最優模型ARIMA(1，1，2)(1，1，2)12，平均絕對百分比誤差均小于10%，均方根誤差均小于20[10]，顯示ARIMA模型預測朝陽市丙型肝炎未來的走勢及發病數，預測精度高，效果好。運用構建的最優模型對2021年12個月丙肝發病數進行預測，若2021年朝陽市疫情的發病情況屬于正常范疇，則實際發病數應落在預測值95%置信區間內；若2021年朝陽市疫情的發病情況呈現暴發或流行趨勢，則實際發病數處于預測值95%置信區間外，建議疾控機構及衛生管理部門快速響應，控制疫情蔓延。研究結果顯示朝陽市2021年丙肝發病數呈上升趨勢，延續了2009—2020年丙肝的發病走勢，這與荊州市[11]、包頭市[12]流行趨勢相同，與各級醫療機構實驗室檢測技術的提高、疾病篩查敏感性的增強、各級疾控機構對傳染病直報工作的督導有關。在未來3月發病數有所上升，考慮與2月是中國農歷新年，就醫量明顯下降，3月新年過后，大量患者醫院就醫而導致病例增多。提示衛生管理部門應在3月加強對丙肝的防治及管理工作，做好宣傳，提高大眾防病、控病意識。

運用ARIMA模型進行丙肝預測應保證充足、完整的基礎數據，一般要求具有30個以上的時間序列數據，7～8個以上的季節周期月發病率序列值。本研究數據包含了12年共144個月的發病數，滿足ARIMA建模對數據的要求，這從一定程度上降低了ARIMA模型本身的局限性。因僅應用了“傳染病報告信息管理系統”上報的監測數據而丙肝的流行狀況往往受到經濟水平、社會環境、政治因素、人口流動和生活方式等多種因素的影響[13]。當影響丙肝流行的因素發生重大變化時，如疫苗的普及，衛生條件的改善等，將導致預測值和實際值之間明顯不符，故ARIMA只適合短期預測，不適合長期預測。需在實際應用中，不斷加入新數據，對模型反復的識別及診斷，確定最優模型，今后可多維度分析丙肝發病趨勢，提高預測的準確性，擬合出精度較高的模型[14]。

綜上所述，ARIMA模型對朝陽市丙肝未來的流行趨勢預測效果較好，這對了解朝陽市丙肝的流行病學特征、流行趨勢、未來防治重點及制定相應的預防控制措施，防止丙肝的暴發及流行具有重要的公共衛生意義，可為丙肝的防治提供科學參考。