基于康奈爾筆記法的Nyquist判據教學方法研究

王立國， 劉 麗

（哈爾濱工業大學電氣工程及自動化學院，化工與化學學院，哈爾濱150001）

0 引 言

自動控制原理課程中的Nyquist 穩定判據是美國Harry Nyquist于1932 年提出的用于確定動態系統穩定性的一種圖形方法［1-3］。Nyquist穩定判據的貢獻突出在兩方面［4-8］：①從時域到頻域，解決了微分方程模型的復雜求解問題；②應用開環傳遞函數分析閉環系統的穩定性，降低了求解的維數。但由于Nyquist穩定判據需要根據s平面上奈氏圖與（-1，j0）點的包圍關系來進行定量分析，會對初學者造成如下困惑［9-10］：①在（-∞，＋∞）內奈氏圖與實軸多次相交時難以把握環繞次數；②當奈氏圖從無窮遠處開始時，起點與終點間如何構成封閉曲線難以判斷。教學中經常發現Nyquist穩定判據的應用誤判，亟待探究一種易于理解的Nyquist判據教學方法。

康奈爾筆記法由康奈爾大學的Walter Pauk 博士提出［9］，以Keywords（關鍵詞）、Notes（注解）及Summary（概括）為主要特征，涵蓋Record（記錄）、Reduce（簡化）、Recite（背誦）、Reflect（補充）、Review（復習）5 個階段，故又稱為5R筆記術，目前該方法已在化學、生物、醫學、計算機教學與深度閱讀、英語閱讀及大學英語聽力理解中得到成功應用［11-15］。鑒于Nyquist穩定判據機理分析的抽象性、分析對象的多樣性，應用康奈爾筆記法建立其思路復雜的學習與求解方案尤其必要。

本文以哈爾濱工業大學-伊頓聯合實驗室為依托，針對Nyquist穩定判據教學及實踐教學中存在的問題，從教學理念、教學內容、教學方法等實踐環節方面進行改進。依據康奈爾筆記法將Nyquist 穩定判據適用的穩定性分析進行5R 歸納，總結為開環傳遞函數極點分析、幅頻特性與相頻特性分析、典型環節頻率特性、逆時針環繞(-1，j0)點次數分析、正負穿越分析、開環Nyquist曲線不能構成閉合軌跡分析等特定學習要點，注解其作用與實質。所做工作有助于學生對Nyquist穩定判據內容的深入理解，教學思路構建與具體案例相結合，促進自動控制原理這一課程教學與國際知名院校的接軌。

1 康奈爾筆記法

康奈爾筆記法是根據艾賓浩斯遺忘曲線［16］展開的，是以5R為特征的集記錄、復習、自測和思考于一體的筆記方法。通過筆記本三欄區間劃分，將課前預習、自測與復習相結合，快速、準確地進行課堂記錄，方便快速查找重點、有條理地學習、提煉內容要點、有針對性地思考；康奈爾筆記法的核心在于記錄、簡化、背誦、補充與復習。以Nyquist 穩定判據學習為背景，相應的康奈爾筆記總結如下。

1.1 Record（記錄）

Record（記錄），在最大的筆記欄（Notes）中先進行快速直接的記錄與收集，突出記錄對象的本質特征、數學機理與應用條件。

（1）Nyquist穩定判據的基本概念。如圖1 所示，Nyquist穩定判據：立足于Cauchy定理之上，設P 為系統在右半s平面開環極點數、Z為系統在右半s平面閉環極點數；當ω 從-∞變化到＋∞時，系統的開環頻率特性G（jω）H（jω）按逆時針方向包圍(-1，j0)點次數為N，定義Z ＝P-N，則閉環控制系統穩定的充分必要條件是Z ＝0。

（2）Nyquist穩定判據的前期知識點復習。如圖2所示，Cauchy定理：設Ω 是復平面的一個單連通的開子集，f：Ω→ 是一個Ω 上的全純函數；設γ 是Ω 內的一個分段可求長的簡單閉曲線；無論γ是自交還是卷繞數多于1，只要γ能夠通過連續形變收縮為Ω 內的一點，則滿足：

圖1 Nyquist穩定判據的基本知識點總結

與G（jω）H（jω）相對應，設F( s )為s 平面內的函數、L 為s 平面內逆時針旋轉的封閉曲線且不經過F( s )的零極點；P1為F( s )位于封閉曲線L 內的極點數、Z1為F( s )位于封閉曲線L 內的零點數；N1為F( s )按逆時針方向包圍(0，j0)點次數，則F( s )穩定的充分必要條件是Z1＝P1-N1＝0。

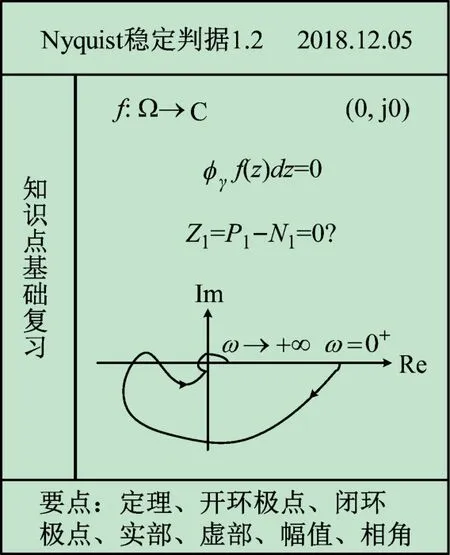
圖2 Nyquist穩定判據學習的前期知識概括

1.2 Reduce（簡化）

Reduce（簡化），提煉重點，專注于從紛繁冗雜的知識信息中獲取關鍵詞、關鍵語句，提綱契領，以便跟上授課速度，提高課堂學習效率。Nyquist 曲線繪制規則：

（1）時域到頻域的計算基礎

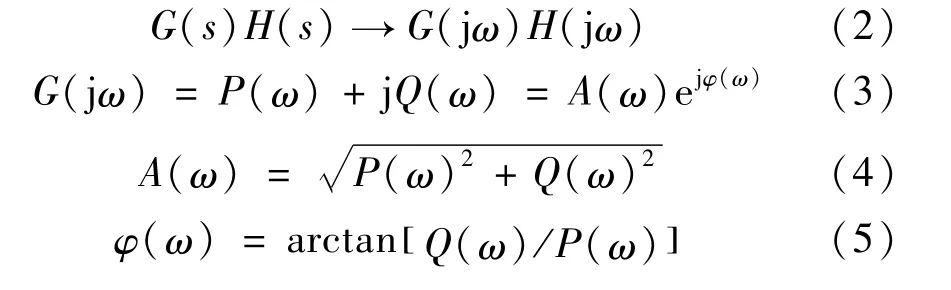
（2）頻域傳遞函數的環節簡化。如圖3 所示，式（2）～（5）可分為如下特征環節：

圖3 傳遞函數的特征環節奈氏圖

比例環節

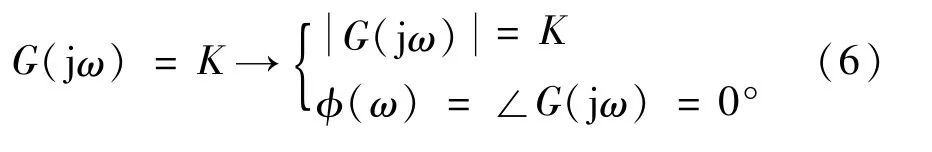
積分環節

慣性環節

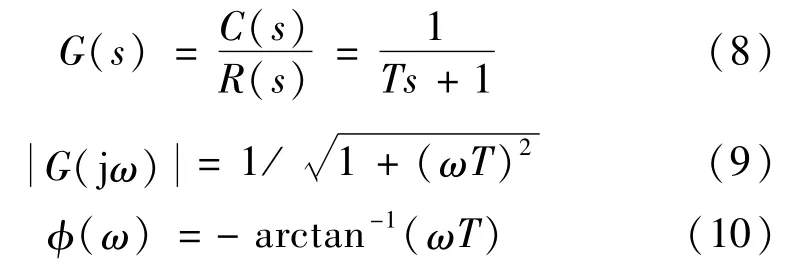
振蕩環節

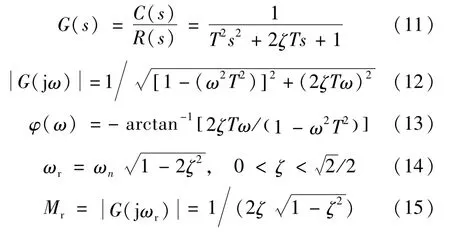
微分環節

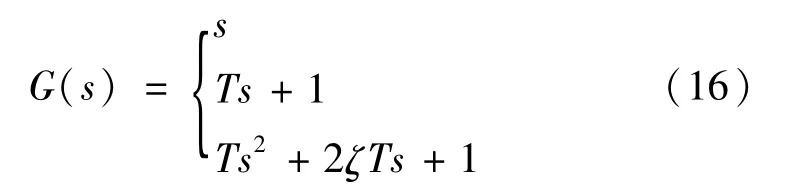
滯后環節

1.3 Recite（背誦）

Recite（背誦），通過重點與資料的對照，轉化出可以執行的學習行動。核心思想在于突出內容的實質與深度，力求精簡，方便記憶。根據講義，Nyquist穩定判據的應用準則總結為如下兩種情況：

（1）奈氏圖與負實軸(-∞，0 )只有一個交點。① 起點G（0＋）H（0＋）和終 點G（＋∞）H（＋∞）；②與實軸對稱補足( -∞，0-)部分奈氏圖；③確定P，應用Z ＝P - N 進行穩定性判定，其中N 為在( -∞，＋∞)區間內G（jω）H（jω）按逆時針方向包圍( -1，j0)點次數； ④ 如圖4 所示， 以為終點、( -1，j0)為起點構建矢量，然后以(-1，j0)為圓心、令所構建矢量沿著奈氏圖（逆時針／順時針）旋轉，判斷從到轉過的角度α，若α ＝n·( 2π)，n ＝1，2，…，則N ＝2n；若矢量逆時針繞(-1，j0)旋轉，則N為正、反之為負。

圖4 Nyquist穩定判據應用1

（2）奈氏圖與負實軸(-∞，0 )有多個交點。①確定起點G（0＋）H（0＋）和終點G（＋∞）H（＋∞）；②正穿越：當ω∈ (0，＋ ∞)，開環幅相曲線（Nyquist 曲線）從s上半平面穿過負實軸的(-∞，-1 )段到s 下半平面，穿越次數定義為N＋；反之稱為負穿越，穿越次數定義為N-；③ 要點：ω∈ (0，＋ ∞)，穿過負實軸的(-∞，- 1 )段；( -1，0 )段穿越無效；④ 與Z ＝P -N 相對應，此時Nyquist 穩定判據定義為Z ＝P -2 (N＋-N-)，詳見圖5。

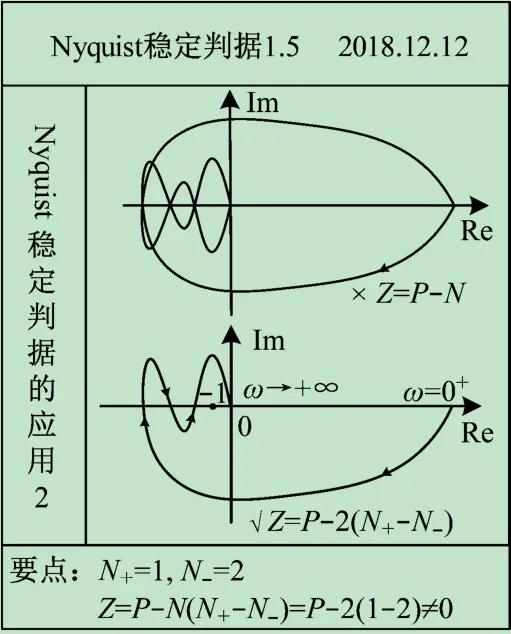
圖5 Nyquist穩定判據應用2

1.4 Reflect（補充）

Reflect（補充），對Nyquist穩定判據常規有了了解后，對于開環傳遞函數中包含積分環節的奈氏圖需要單獨處理，因為此時奈氏圖起始于無窮遠處，不構成封閉的曲線（不滿足Cauchy 定理），此時需要補足積分環節造成的缺陷。

當控制系統開環傳遞函數為如下形式時：

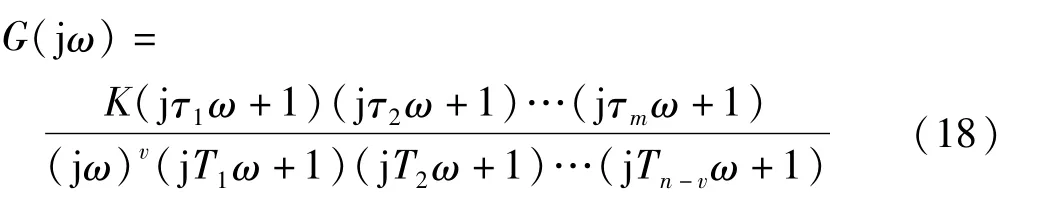
由于系統中含有v 個積分環節，奈氏圖起始于無窮遠處，開環Nyquist 曲線不能構成閉合軌跡，無法確定Nyquist曲線包圍(-1，j0)點的圈數N。

如圖6 所示，需要先把開環幅相曲線補為封閉曲線，方法是從原開環幅相曲線的ω ＝0＋這一點，逆時針補畫半徑為無窮大的v ×90°圓弧，并用虛線表示；即一個積分環節補90°，v個積分環節補v×90°。

圖6 含積分環節奈氏圖Nyquist穩定性分析

教學過程中，體現的難點在于，補足v ×90°后，學生不清楚后補曲線的方向性，此時最簡捷的方向判定方法就是令后補曲線的方向與原奈氏圖方向一致，而且只分析ω∈(0，＋∞ )這一部分奈氏圖。

1.5 Review（復習）

Review（復習），Nyquist穩定判據在筆記中主要突出頻域分析、奈氏圖繪制、不同情況下的Nyquist 判據表現形式等，核心在于總結關鍵詞，提煉應用準則、濃縮要點。與式（18）相對應（n個極點、m個零點）。

1.5.1 頻率特性

涵蓋幅頻特性與相頻特性，其中實頻特性與虛頻特性分別表示如下：

1.5.2 繪制奈奎斯特圖

如圖7 所示，核心問題：① ω→0＋時，低頻段從何處出發？②ω→＋∞時，高頻段以何種姿態收斂？③在ω為何值時穿越實軸和虛軸？④ 與坐標軸的交點為多少？給出每一點處的幅值與相角。

（1）ω→0＋時，低頻段的表達式為：

ω→0＋時，滿足表1 所示計算數據。

表1 不同數量積分環節的出發點幅值與相角分析

（2）ω→＋∞時，高頻段幅頻和相頻特性為：

滿足如下規律：①n -m ＝1，曲線沿負虛軸向原點收斂；②n - m ＝2，曲線沿負實軸向原點收斂；③n-m ＝3，曲線沿正虛軸向原點收斂。

圖7 所示是對Nyquist穩定判據的圖形總結，可解決學生對起始于無窮遠處奈氏圖畫圖、補足全圖及穩定性分析的困惑，簡單直觀、易于理解。

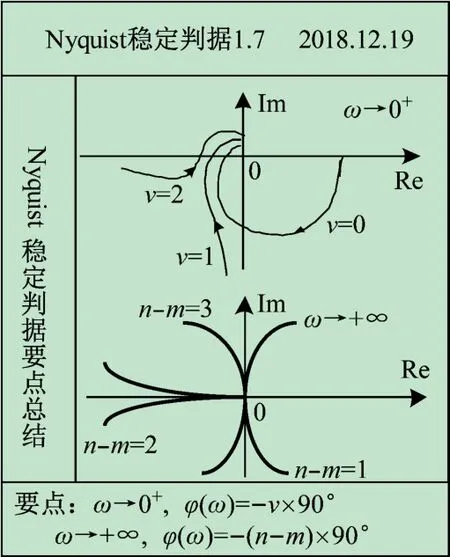
圖7 Nyquist穩定判據準則總結

2 實例分析

已知某單位負反饋系統開環傳遞函數為：

試用奈奎斯特判據判斷閉環系統穩定性。

應用康奈爾筆記法求解過程如圖8 ～11 所示。

圖8 所示為時域到頻域、起點到終點的計算過程；圖9 所示為奈氏圖與實軸交點的計算過程；圖10 ～11分別展示了如何將起始于無窮遠處的奈氏圖補足及應用Z ＝P -N及Z ＝P -2 (N＋-N-)進行穩定性分析的具體過程。與圖1 ～7 相對應，借助于康奈爾筆記法，此實例可將Nyquist 穩定判據應用過程系統、直觀地展示給學生。

圖8 Nyquist頻率特性分析

圖9 奈氏圖相關繪制過程

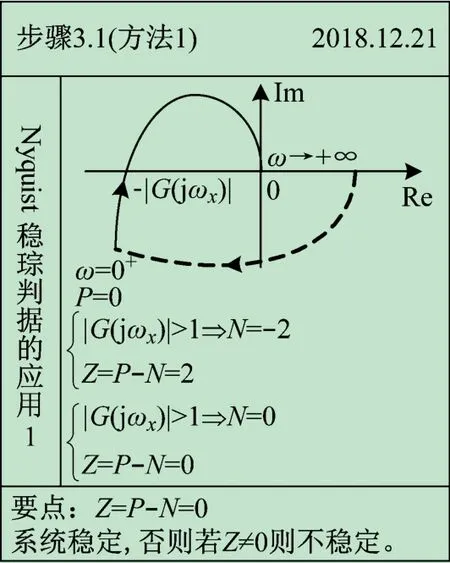
圖10 應用Z ＝P-N方法的Nyquist穩定性分析

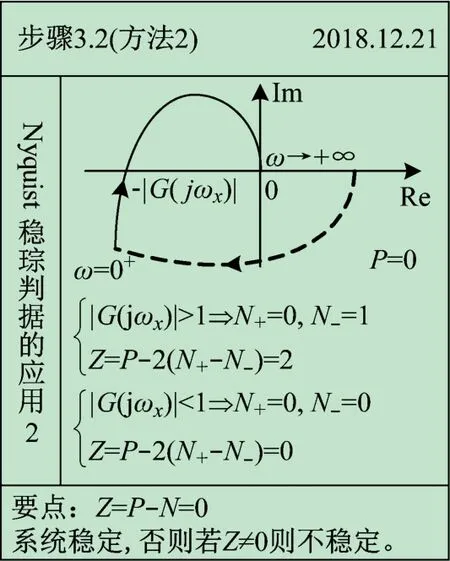
圖11 應用正負穿越方法的Nyquist穩定性分析

3 結 語

基于康奈爾大學筆記法思想，將其與自動控制原理教學中的Nyquist 穩定判據有機結合，建立機理分析、繪制規則、穩定判據與康奈爾大學筆記之間的邏輯教學體系，突出記錄、簡化、背誦、補充與復習5 個環節教學方法的改進；以哈爾濱工業大學-伊頓聯合實驗室為依托，提出了具有電氣工程教學特色的康奈爾大學筆記法思路。2018 年，將康奈爾大學筆記法思想融于自動控制原理雙語教學中，突出圖1 ～7 所示的教學體系模式，取得了較為理想的授課效果，15 人的大四授課對象中保研比例為93%，這在一定程度上驗證了所提康奈爾大學筆記法教學思想的有效性。