淺析教學(xué)中的關(guān)聯(lián)速度問(wèn)題

范財(cái)政

(大嶺山中學(xué)高中部 廣東 東莞 523820)

1 提出問(wèn)題

在速度的合成與分解問(wèn)題中，常遇到以下這個(gè)經(jīng)典例題.

【例題】如圖1所示，某人站在岸上通過(guò)繞定滑輪的繩子向岸邊拉船.他拉繩子速率不變，當(dāng)拉船的繩子與水平面成α角時(shí)，船前進(jìn)速度u多大?

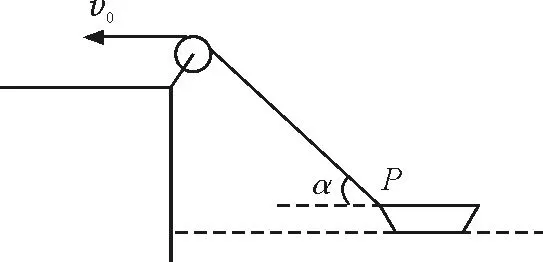
圖1 例題題圖

學(xué)生們通常以圖2的方式分解[1]，認(rèn)為u=v1=v0cosα這種分解方式顯然錯(cuò)誤，因?yàn)榇谶\(yùn)動(dòng)過(guò)程中明顯沒(méi)有豎直向上的分運(yùn)動(dòng).

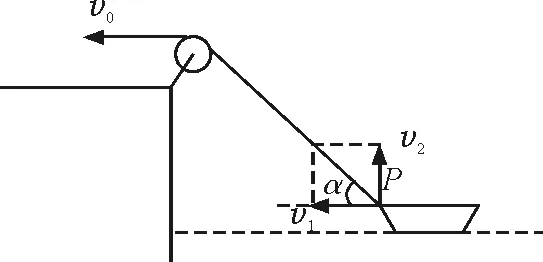
圖2 學(xué)生解題常用分解方式

在教學(xué)過(guò)程中，有許多教師認(rèn)為這是一個(gè)速度分解的問(wèn)題，常用圖3的方式進(jìn)行分解計(jì)算，船速是合速度，分解為沿繩的分速度v1和垂直于繩的另一個(gè)分速v2.因此，繩子的速度是v0根據(jù)三角形幾何關(guān)系得到船速

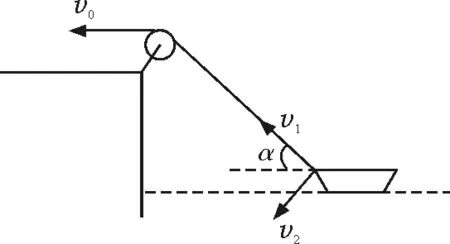
圖3 教師解題常用分解方式

這樣講解這道例題，存在什么問(wèn)題？學(xué)生經(jīng)常會(huì)產(chǎn)生疑問(wèn)，為什么船速是合速度，而繩速卻是分速度？而且為什么兩個(gè)分速度v1和v2必須垂直？

針對(duì)學(xué)生的問(wèn)題，教師的解釋如下：合運(yùn)動(dòng)與分運(yùn)動(dòng)的定義是物體實(shí)際的運(yùn)動(dòng)是那兩種運(yùn)動(dòng)的合運(yùn)動(dòng)，那兩種運(yùn)動(dòng)就是這個(gè)實(shí)際運(yùn)動(dòng)的分運(yùn)動(dòng).

在上述例題中，船沿水平方向的實(shí)際運(yùn)動(dòng)明顯就是合運(yùn)動(dòng)，所以沿繩和垂直于繩方向的兩個(gè)運(yùn)動(dòng)就是分運(yùn)動(dòng).

v1和v2如果不垂直，如圖4所示，v2在繩子方向上投影不為零，所以還應(yīng)該把v2分解.v0=v1-v2sinα，結(jié)果還是分解為圖3的情況.只有v1和v2垂直，v2在繩子的方向上投影才為零，也就是v2不能再分.

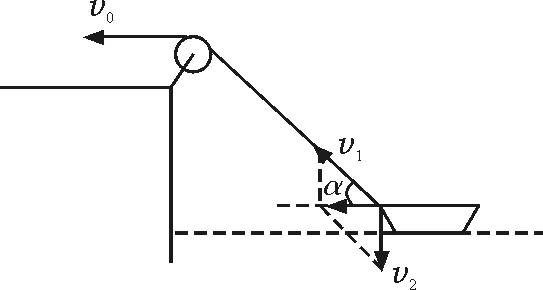
圖4 v1和v2不垂直的分解方式

那么這樣解釋是否正確？

2 分析問(wèn)題

采用速度分解的方法來(lái)解決上述例題，有許多教師認(rèn)為這是錯(cuò)誤，陳鋼等論述了這個(gè)觀點(diǎn).他們認(rèn)為[2]，上述例題中船速與繩速的關(guān)系根本就不屬于運(yùn)動(dòng)分解的問(wèn)題，既非繩速的分量為船速，亦非船速的分量為繩速.船頭沿水平面運(yùn)動(dòng)，行船的速度與拉繩的速度并不構(gòu)成速度分解與合成的關(guān)系，因?yàn)轱@然繩速與船速是因果關(guān)系，拉繩為“因”而行船為“果”，這不符合運(yùn)動(dòng)分解的邏輯關(guān)系.

而筆者認(rèn)為運(yùn)動(dòng)的分解定義中，分運(yùn)動(dòng)具有相對(duì)獨(dú)立性，分運(yùn)動(dòng)間互不相干，任何一個(gè)分運(yùn)動(dòng)可以獨(dú)立存在.而上述例題中，v1,v2兩個(gè)分運(yùn)動(dòng)并不能獨(dú)立存在，如果沒(méi)有繩速,v2就不存在，更沒(méi)有船速.

因此，使用速度分解的方法解決關(guān)聯(lián)速度問(wèn)題存在爭(zhēng)議，筆者建議使用別的更合理的方法，避免爭(zhēng)議也方便學(xué)生理解.

3 關(guān)聯(lián)速度問(wèn)題的解法

3.1 關(guān)聯(lián)速度問(wèn)題的常規(guī)解法

在解決上述例題前，先弄明白上述的船速和繩速應(yīng)當(dāng)屬于哪一種關(guān)系？圖5中船是因?yàn)槔K拉而動(dòng)的，拉繩是“因”，而船行是“果”，速度有關(guān)聯(lián)，它們符合關(guān)聯(lián)速度的特征，是典型的“關(guān)聯(lián)速度”問(wèn)題.

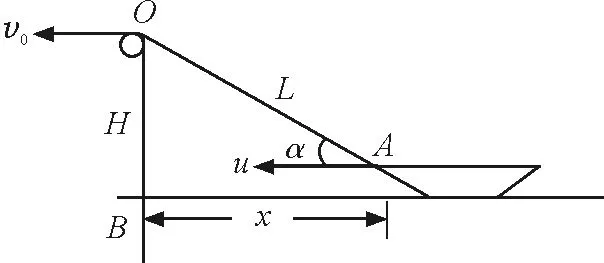
圖5 船速與繩速關(guān)聯(lián)示意圖

在機(jī)械運(yùn)動(dòng)中普遍地存在著速度的關(guān)聯(lián)關(guān)系，關(guān)聯(lián)速度的基本特征是，一個(gè)獨(dú)立的運(yùn)動(dòng)導(dǎo)致另一個(gè)相關(guān)聯(lián)的運(yùn)動(dòng)，這兩個(gè)運(yùn)動(dòng)被幾何關(guān)系約束，因此往往可以寫(xiě)出確定它們之間幾何關(guān)系的“約束方程”，根據(jù)圖5對(duì)拉船問(wèn)題可以寫(xiě)出約束方程

x2+H2=L2

(1)

兩邊對(duì)t求導(dǎo)后，得

(0≤α<90°)

對(duì)于其他的典型關(guān)聯(lián)速度問(wèn)題，例如馬拉車(chē)，滑輪拉重物等[2]，都可以使用約束方程來(lái)解決.

上述的關(guān)聯(lián)速度問(wèn)題的解決方法看似完美，但是高中的學(xué)生并沒(méi)有學(xué)過(guò)導(dǎo)數(shù)，如果對(duì)中學(xué)生講解上述方法，那么教師和學(xué)生必然是事倍功半.

3.2 關(guān)聯(lián)速度問(wèn)題的中學(xué)解法

在中學(xué)雖沒(méi)有學(xué)過(guò)導(dǎo)數(shù)，但是學(xué)過(guò)微元法，因此，教師可以通過(guò)微元法來(lái)講解關(guān)聯(lián)速度問(wèn)題.如圖5所示，設(shè)經(jīng)過(guò)極短的Δt時(shí)間，繩子收縮長(zhǎng)度ΔL，船的位移是Δx.經(jīng)過(guò)Δt后約束方程依然成立

(x-Δx)2+H2=(L-ΔL)2

(2)

將式(1)代入式(2)化簡(jiǎn)得

(3)

將式(3)兩邊除以Δt得

因?yàn)棣極短，相對(duì)2L，ΔL可忽略；相對(duì)2x，Δx也可以忽略

所以可得

(4)

由此可見(jiàn)，用微元法得出的結(jié)果與導(dǎo)數(shù)方法相同，而且又能使中學(xué)生理解.

為便于學(xué)生理解，還可以從能量的角度講解關(guān)聯(lián)速度問(wèn)題.

為什么許多學(xué)生常以圖2的方式分解繩速？因?yàn)槭芰Φ姆纸獾亩▌?shì)思維的影響，認(rèn)為速度也能這樣分解.

根據(jù)力的分解思維，學(xué)生很容易將繩拉船的力分解為水平方向和豎直方向的兩個(gè)分力.速度與力的乘積又是功率，因此我們可以得到啟發(fā)，找到適合中學(xué)生的解題方法.

如圖1所示，人拉繩做功大小與繩拉船做功大小是否相等？在忽略滑輪阻力的情況下，答案是肯定的.再因?yàn)槿藢?duì)繩做功的時(shí)間與繩對(duì)船做功時(shí)間相同，所以功率相同[3].

根據(jù)以上分析，假設(shè)人拉繩的力是F，則人拉繩的功率P1=Fv0.

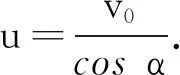
對(duì)于類似的馬拉車(chē)、滑輪拉重物的問(wèn)題，也可以使用功率相等的方法解決問(wèn)題.

4 總結(jié)

在教學(xué)過(guò)程中常遇見(jiàn)的關(guān)聯(lián)速度問(wèn)題，有許多教師都是以運(yùn)動(dòng)分解的方法來(lái)教學(xué)生.筆者認(rèn)為運(yùn)動(dòng)分解的概念還是不能與關(guān)聯(lián)速度混淆.針對(duì)關(guān)聯(lián)速度的問(wèn)題，常規(guī)的解法就是運(yùn)用“約束方程”，但是這個(gè)方法運(yùn)用了導(dǎo)數(shù)的知識(shí)，所以教師可以理解，而中學(xué)生卻不能.總之，為便于中學(xué)生理解，建議教師在講解關(guān)聯(lián)速度的問(wèn)題時(shí)，可以用微元法或從能量的角度來(lái)講解.