立體幾何中平行和垂直問題的證明

■江蘇省華羅庚中學 李普紅

平行與垂直關系的證明是高考考查立體幾何的高頻考點，大部分問題都可以用傳統(tǒng)的幾何方法解決，有一部分問題需要建立空間直角坐標系利用空間向量解決。用傳統(tǒng)法解題時，應注重線線平行、線線垂直、線面平行、線面垂直、面面平行、面面垂直等問題的性質定理和判定定理的靈活應用。用向量法解題時，應建立恰當的空間直角坐標系，準確表示各點與相關向量的坐標。

考向一:證明線面平行

例1如圖1，已知空間幾何體BACDE 中，△BCD與△CDE 均是邊長為2的等邊三角形，△ABC 是腰長為3，底邊為BC 的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD。

（1）試在平面BCD 內作一條直線，使得直線上任意一點F 與E 的連線EF 均與平面ABC 平行，并給出證明；

（2）求三棱錐E-ABC 的體積。

圖1

解析：（1）如圖2 所示，取DC 的中點為N，BD 的中點為M，連接 MN，則MN 即為所求。

連接EM，EN，取BC的中點H，連接AH。

因為△ABC 是腰長為3的等腰三角形，H 為BC 的中點，所以AH ⊥BC。

又平面ABC⊥平面BCD，平面ABC∩平面BCD=BC，AH ?平面ABC，所以AH⊥平面BCD。

同理可證EN⊥平面BCD。

所以EN∥AH。

又M，N 分別為BD，DC 的中點，所以MN∥BC。

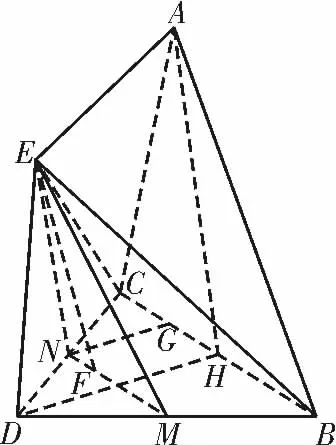
圖2

又MN∩EN=N，MN?平面EMN，EN?平面EMN，所以平面EMN∥平面ABC。

又EF ?平面EMN，所以EF ∥平面ABC，即直線MN 上任意一點F 與E 的連線EF 均與平面ABC 平行。

（2）連接DH，取CH 的中點為G，連接NG，則NG∥DH。

由（1）可知EN∥平面ABC，所以點E 到平面ABC 的距離與點N 到平面ABC 的距離相等。

又△BCD 是邊長為2的等邊三角形，所以DH ⊥BC。

又平面ABC⊥平面BCD，平面ABC∩平面BCD =BC，DH ?平面BCD，所以DH ⊥平面ABC，所以NG⊥平面ABC。

考向二:證明面面平行

例2如圖3，在長方體 ABCD-A1B1C1D1中，AB=1，AD=2，E，F分別為AD，AA1的中點，Q 是BC 上一個動點，且BQ=λQC（λ＞0）。

（1）當λ=1 時，求證：平面BEF∥平面A1DQ。

（2）試問：是否存在λ，使得BD⊥FQ? 若存在，請求出λ 的值；若不存在，請說明理由。

解析：（1）當λ=1 時，Q 為BC 的中點，因為E 是AD 的中點，所以ED=BQ。

又ED∥BQ，則四邊形BEDQ 是平行四邊形，所以BE∥QD。

圖3

因為E，F 分別是AD，A1A 的中點，所以EF∥A1D。

因為BE∩EF=E，EF?平面BEF，BE?平面BEF，所以平面BEF∥平面A1DQ。

（2）如圖4，連接AQ，BD，FQ。

因為 A1A ⊥平面ABCD，BD ? 平面ABCD，所以A1A⊥BD。

若 BD ⊥FQ，又A1A，FQ?平面A1AQ，且A1A ∩FQ=F，所以BD⊥平面A1AQ。

因為AQ?平面A1AQ，所以AQ⊥BD。

在矩 形ABCD 中，由AQ ⊥BD，得△AQB∽△DBA，則所以AB2=AD·BQ。

圖4

考向三:證明線面垂直

例3如圖5，在四棱錐P-ABCD 中，四邊形ABCD 為正方形，PA⊥平面ABCD，PA=AB，M 是PC 上一點，且BM⊥PC。

（1）求證：PC⊥平面MBD；

（2）求直線PB 與平面MBD 所成角的正弦值。

解析：（1）連接AC，由PA⊥平面ABCD，BD?平面ABCD，得BD⊥PA。

又BD⊥AC，PA∩AC=A，所以BD⊥平面PAC。

又PC?平面PAC，則PC⊥BD。

又PC⊥BM，BD∩BM=B，所以PC⊥平面MBD。

圖5

（2）由（1）知PC ⊥平面 MBD，則∠PBM 是直線PB 與平面MBD 所成角。

易證PB ⊥BC，而BM ⊥PC，不妨設PA=1，則BC=1，

考向四:證明面面垂直

例4如圖6，在四棱錐 P-ABCD 中，底面ABCD 為菱形，∠ABC=60°，PA⊥平面ABCD，E，M 分別是BC，PD 的中點，直線EM 與平面PAD 所成角的正弦值為，點F 在PC 上移動。

圖6

（1）證明：無論點F 在PC 上如何移動，都有平面AEF⊥平面PAD；

（2）當F 恰為PC 的中點時，求二面角C-AF-E 的余弦值。

解析：（1）連接AC，因為底面ABCD 為菱形，∠ABC=60°，所以△ABC 是正三角形。

因為E 是BC 的中點，所以AE⊥BC。

又AD∥BC，所以AE⊥AD。

因為PA ⊥平 面ABCD，AE ?平 面ABCD，所以PA⊥AE。

又PA∩AD=A，所以AE⊥平面PAD。

又AE?平面AEF，所以平面AEF⊥平面PAD。

由此可證明：無論點F 在PC 上如何移動，都有平面AEF⊥平面PAD。

（2）由（1）得AE，AD，AP 兩兩垂直，則以A 為坐標原點，AE，AD，AP 所在直線為x 軸，y 軸，z 軸，建立如圖7所示的空間直角坐標系A-xyz。

因為AE⊥平面PAD，所以∠AME 是EM 與平面PAD 所成的角。

又AD=AB=2a，設PA=2b，則M（0，a，b），所以AM=從而b=a，所 以PA =AD =2a，則A （0，0，0），B（a，-a，0），C（a，a，0），D（0，2a，0），P（0，0，2a）

平行或垂直關系的證明常出現在解答題的第一問，對同學們的直觀想象能力要求很高。特別地，有一類問題是只有在第一問利用幾何法證明了垂直關系，才能在后面的問題中建立空間直角坐標系解題，所以平時應注重這方面的訓練。