基于核心素養“數學運算”的公式教學探究
——以“點到直線的距離”的教學為例

揚州大學附屬中學(225002) 張 順

《普通高中數學課程標準(2017 版)》中明確界定了數學學科的六大核心素養的內涵和水平劃分.其中“數學運算”素養是指“在明確運算對象的基礎上,依據運算法則解決數學問題的素養”,并從理解運算對象、掌握運算法則、探究運算思路和求得運算結果等方面給出了三個不同水平的劃分.

基于數學核心素養之一“數學運算”的培養要求,近日,筆者在所教班級上了一節“點到直線的距離”的課.下面筆者就以此為例談談如何在數學課堂中的落實“數學運算”的培養.

1 教學內容和目標

1.1 教材分析

“點到直線的距離”是蘇教版必修二第二章第6 節的內容,旨在解決“直線l:Ax+By+C=0 外一點P(x0,y0)到直線l的距離”.教材通過上節課已經證明的一道例題四邊形ABCD為平行四邊形,接著追問如何求平行四邊形ABCD的面積,自然引到求點到直線的距離.教材對于該例題給出了兩種解法“交點法”、“三角形面積法”,接著指出“交點法”計算量較大,“三角形面積法”計算簡潔,再通過該方法求證出一般情形下“點到直線的距離公式”.

1.2 學情分析

高一第二學期學生在此之前已經學習了兩條直線平行與垂直的判定、兩點間距離公式和中點坐標公式等內容,已經具備了一定的利用代數方法解決幾何問題的能力.“點到直線距離”小學、初中時就也就有所涉及例如求三角形面積時作出一邊上的高,這個概念學生并不陌生,但學生由用尺規量出點到直線距離,上升到利用公式計算得到距離是思維層次的一大步提高.根據我所教班級學生特點學生素質較高,綜合能力較強,同時由于是文科班女生占了絕大多數,學生代數運算,尤其是多字母的代數運算的能力還是不足的特點,本節課立足于提升學生的運算素養,嘗試解釋運算背后的算理,讓學生能有所得.

1.3 教學目標

(1)通過點到直線距離公式的推導,滲透化歸思想.

(2)通過點到直線距離公式推導的幾種證法,使學生能理解算法選擇的優劣,探究優化求解的思路,提升數學運算素養.

1.4 教學重難點

重點: 點到直線距離公式的推導;

難度: 對點到直線距離公式推導過程的優化.

2 教學過程

問題1:“點到直線距離”如何定義?

預設1: 過一點作已知直線的垂線,相交于垂足,點到垂足的距離為點到直線距離.

預設2: 已知點到直線上一點的最短距離為點到直線距離.

設計意圖: 該問題一是讓學生明白我們這節課所要研究的問題,二來通過該問題的兩個預設為接下來推導點到直線距離公式的兩種方法作鋪墊.

問題2: 已知直線l:Ax+By+C= 0(A2+B2?= 0)外一點P(x0,y0),求點P到直線l的距離?

預設1: 先求過點P垂直l的直線,再求兩直線交點,最后用兩點間距離公式.該方法可能遇到的問題: 學生不會求過點P與l垂直的直線;求不出交點;求不出兩點間距離.

預設1: 先求過點P垂直l的直線,再求兩直線交點,最后用兩點間距離公式.該方法可能遇到的問題: 學生不會求過點P與l垂直的直線;求不出交點;求不出兩點間距離.

設過點P與l垂直的直線為l′:Bx?Ay+D=0,由于過點P(x0,y0)故有Bx0?Ay0+D=0,將D=Ay0?Bx0代入l′得到l′:Bx ?Ay+Ay0?Bx0=0 從而突破第一個難點.

最后再求兩點距離:

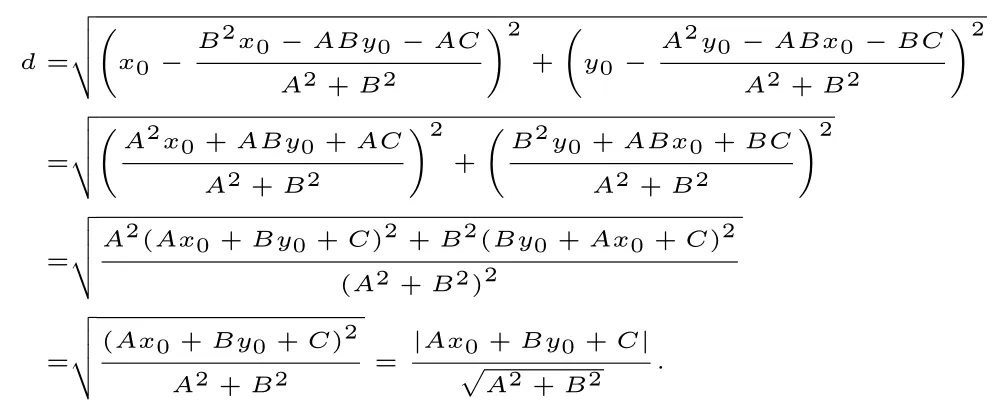
合理的進行通分合并同類項,學生運算中常見的問題是不考慮代數式得結構特征,“暴力”分解多項式從而破壞式子結構,而由于運能能力的不足,對于拆分后的式子往往沒有辦法更進一步的化簡,使得計算難以進行下去.

追問1: 上面解法較為繁瑣,計算容易出錯,那么有沒有更好的解法呢?

教師在黑板上板書如圖(1) 所示圖形, 提示學生要求PQ還能有什么方法.學生在圖形提示下會聯想到利用三角形面積求出PQ,于是有下面的解法.

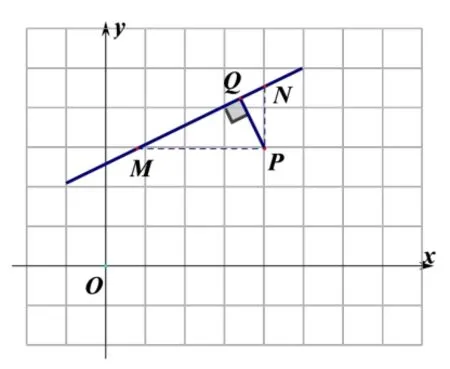
圖(1)

設P(x0,y0), 則M(xM,y0),N(xN,y0) 代入直線方程解得同理NP=；因為所以

追問2: 為什么通過三角形等面積法轉化后計算量會減少?

設計意圖: 學生能看懂該解法,但是如果沒有老師作圖提示能主動聯想通過三角形面積算兩次得到斜高的學生應該不會很多.再者利用該方法為什么能起到簡化運算的效果,是什么原因使然,對于這個問題學生想不到去追問,但這恰恰是比較重要的.通過轉化與化歸將求斜高轉化為求兩條平行于坐標軸的直角邊長度,這種轉化能簡化運算的原因就在于其問題研究的坐標系是直角坐標系, 在直角坐標系中, 平行于坐標軸的兩點距離是容易得到的|x1?x2|或者|y1?y2|,而在其它情況下會用到兩點距離公式增加計算.

預設2: 學生會想到利用直線上一點與已知點求兩者距離最小值來表示距離.

通過數學建模, 學生能建立直線上一點與已知點的函數關系式.設直線l上一點為Q(x,y), 定點P(x0,y0),于是PQ=由 于Q在 直 線l上,PQ最小時P,Q在與l垂直的直線上, 由預設(1)中解得的方程有計算時需要有目標意識, 需要我們求得的表達式結構中有(x ?x0),(y ?y0) 這兩個量, 于是對上面方程組可以變形為又觀察目標結構中有(x ?x0)2+(y ?y0)2,所以想到將方程組兩式平方再相加,得到(A2+B2)[(x ?x0)2+(y ?y0)2] =(Ax0+By0+C)2, 最后得到

設計意圖: 對于多字母運算學生在公式變形式往往像無頭蒼蠅到處亂撞,展開到哪里就到哪里.公式變形前沒能對多要求的目標式的結構有所思考,另一方還需要學生公式變形時有一定的整體意識.這種方法學生不會那么容易想到,教學時需要教師一步步去引導,指導學生如何算,怎么想.

問題3: 前面探討過通過構造三角形, 利用三角形面積來求高, 是否還有其他構造圖形的方式?

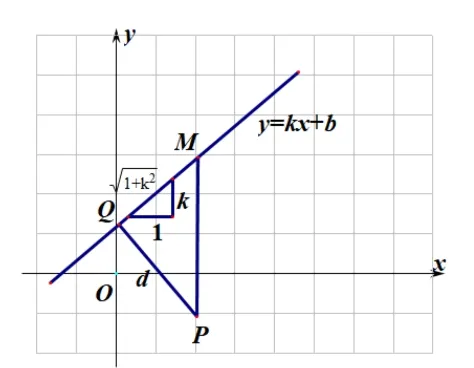
圖(2)

教師板書如圖(2) 所示圖形,為了突出重點,這里只研究直線k存在且大于零情況.教師提示學生利用相似三角形知識.在老師的提示下學生能夠得到大三角形MPQ與小直角三角形相似, 因為MP=|kx0+b ?y0|,即, 最后再化為直線一般式下情形即可得證.

設計意圖: 這種創造性的思維,教師預想的學生不可能構造出這種圖形,所以需要板書出來直接給學生,學生通過這樣的構造能體會到數形結合的思想,覺得數學美麗有趣就是成功!

3 小結

本節課用4 種方法證明了點到直線的距離: 交點法,面積法,構造函數法,構造相似圖形法.交點法難算,但是解析幾何證明題中少不了計算,當我們沒有什么巧妙解法時,計算也許是唯一的路徑,教學中也要讓學生能有面對復雜計算能算下去的信心.面積法大大減少了計算,同學們也要對其背后原因有所了解,因為直角坐標系下平行于坐標軸的線段長度容易表示.構造函數的方法是本節課重點強調的一種方法,該方法首先要能準確建模構造出函數,列出目標表達式和約束條件,而求解最值化簡過程中需要有整體思想和目標意識,時刻聯想到所要求的的目標結構.最后為了提升學生學習數學興趣,介紹了一種巧妙的構造相似三角形方法,講解這種方法主要是讓學生體會數學的美妙.