基于核心素養的高考三角函數試題分析及教學啟示

廣東省佛山市順德區第一中學(528300) 楊承根

廣東省東莞市麻涌中學(523000) 駱妃景

廣東省佛山市順德區容山中學(528303) 潘敬貞

云南師范大學數學學院(650500) 唐明超

三角函數是高中數學的核心內容之一,也是歷年高考考查的熱點和重點內容.就三年的全國卷高考真題來看,三角函數試題總體穩定,形式略有創新,趨于綜合化、試題難度有所提升.既考查學生對基本概念、基本公式的理解和應用,又考查了化繁為簡的運算能力以及數形結合、轉化與化歸等數學思想方法,試題著眼于考查學生的數學運算、直觀想象、邏輯推理等數學核心素養.文章整理和分析了2017-2019 三年全國卷關于三角函數的考點, 將試題劃分為8 個常見類型,并對真題進行評析,便于廣大師生了解高考命題規律,為高三一輪復習提供方向和建議.

1 2017-2019年全國卷高考三角函數考點及分析

1.1 考點分析

為了更清晰地分析近三年來全國卷中三角函數這一重要且必考的知識模塊的命題規律,筆者整理得以下表格:

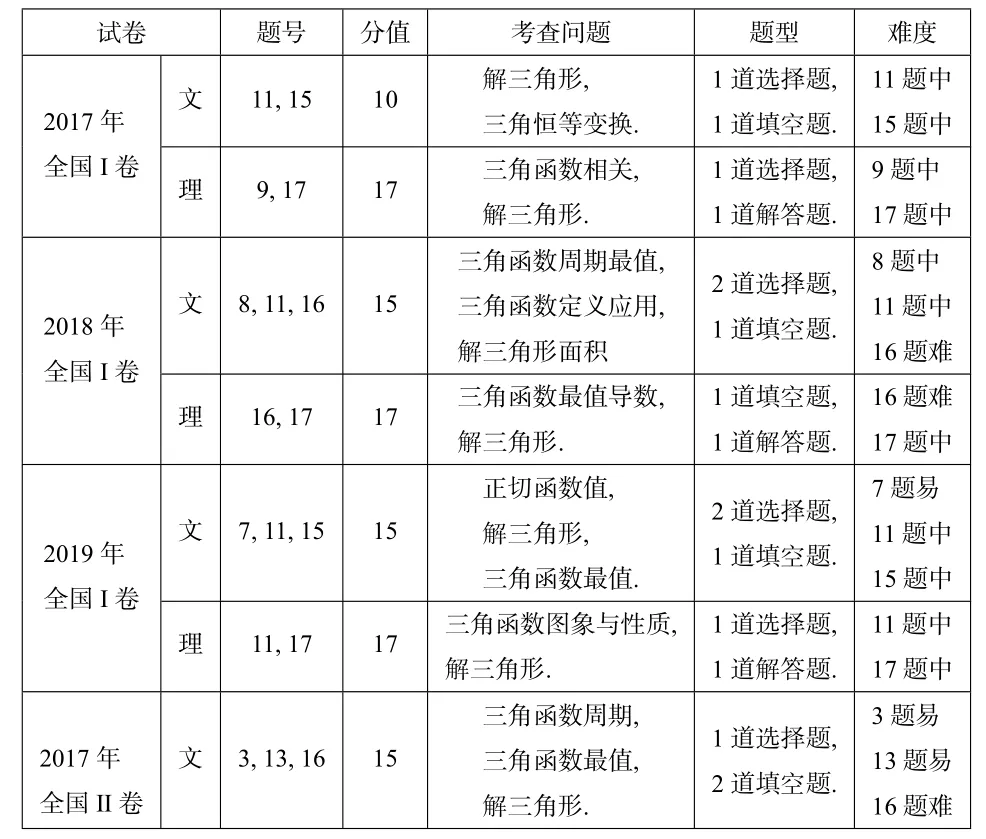
試卷題號分值考查問題題型難度2017年全國I卷文11,15 10解三角形,三角恒等變換.1 道選擇題,1 道填空題.11 題中15 題中理9,17 17三角函數相關,解三角形.1 道選擇題,1 道解答題.9 題中17 題中2018年全國I卷文8,11,16 15三角函數周期最值,三角函數定義應用,解三角形面積2 道選擇題,1 道填空題.8 題中11 題中16 題難理16,17 17三角函數最值導數,解三角形.1 道填空題,1 道解答題.16 題難17 題中2019年全國I卷文7,11,15 15正切函數值,解三角形,三角函數最值.2 道選擇題,1 道填空題.7 題易11 題中15 題中理11,17 17三角函數圖象與性質,解三角形.1 道選擇題,1 道解答題.11 題中17 題中2017年全國Ⅱ卷文3,13,16 15三角函數周期,三角函數最值,解三角形.1 道選擇題,2 道填空題.3 題易13 題易16 題難

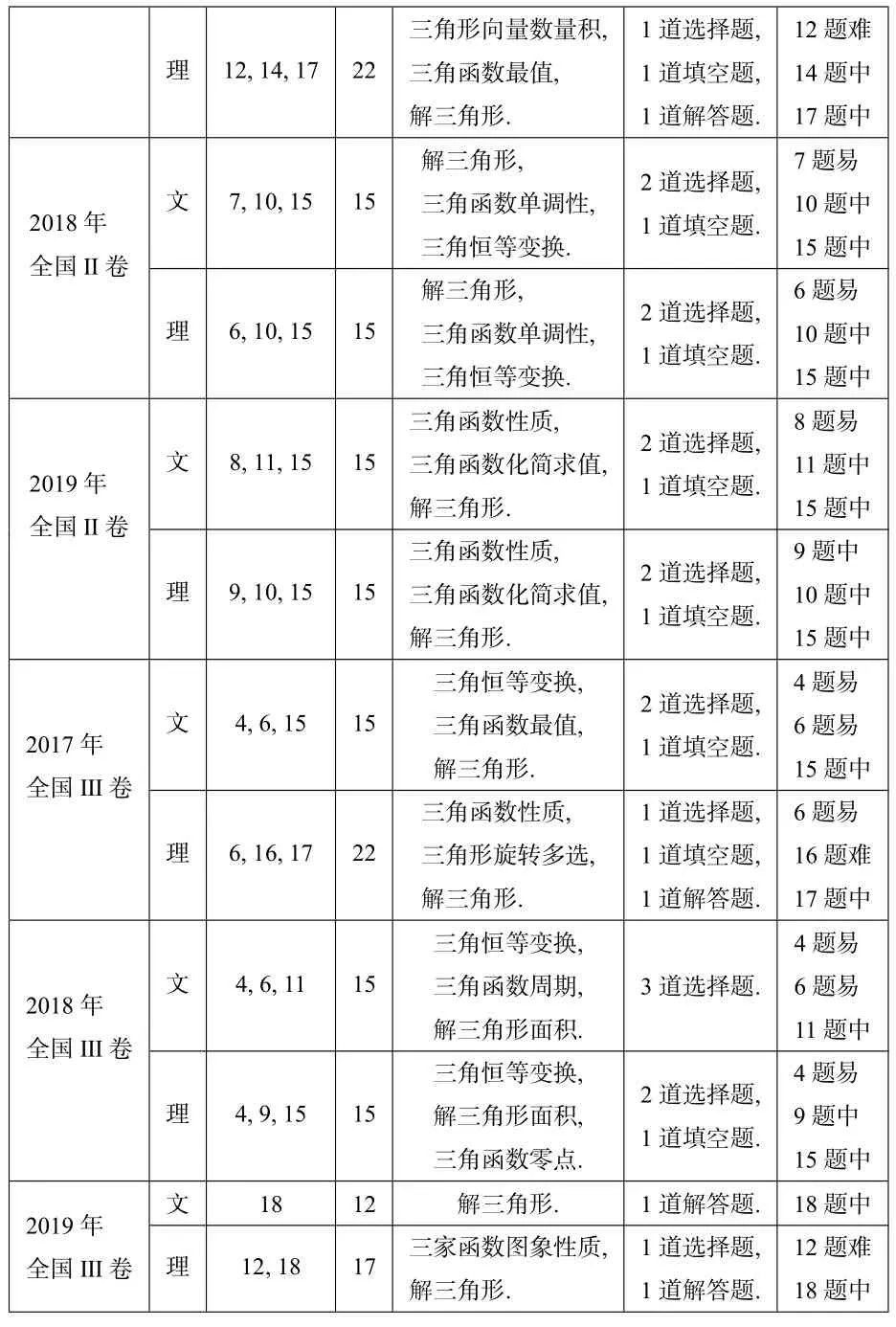
理12,14,17 22三角形向量數量積,三角函數最值,解三角形.1 道選擇題,1 道填空題,1 道解答題.12 題難14 題中17 題中2018年全國Ⅱ卷文7,10,15 15解三角形,三角函數單調性,三角恒等變換.2 道選擇題,1 道填空題.7 題易10 題中15 題中理6,10,15 15解三角形,三角函數單調性,三角恒等變換.2 道選擇題,1 道填空題.6 題易10 題中15 題中2019年全國Ⅱ卷文8,11,15 15三角函數性質,三角函數化簡求值,解三角形.2 道選擇題,1 道填空題.8 題易11 題中15 題中理9,10,15 15三角函數性質,三角函數化簡求值,解三角形.2 道選擇題,1 道填空題.9 題中10 題中15 題中2017年全國Ⅲ卷文4,6,15 15三角恒等變換,三角函數最值,解三角形.2 道選擇題,1 道填空題.4 題易6 題易15 題中理6,16,17 22三角函數性質,三角形旋轉多選,解三角形.1 道選擇題,1 道填空題,1 道解答題.6 題易16 題難17 題中2018年全國Ⅲ卷文4,6,11 15三角恒等變換,三角函數周期,解三角形面積.3 道選擇題.4 題易6 題易11 題中理4,9,15 15三角恒等變換,解三角形面積,三角函數零點.2 道選擇題,1 道填空題.4 題易9 題中15 題中2019年全國Ⅲ卷文18 12解三角形.1 道解答題.18 題中理12,18 17三家函數圖象性質,解三角形.1 道選擇題,1 道解答題.12 題難18 題中

1.2 題型與分值

總體上看,全國卷對“三角函數”的命題風格穩定與創新共存,試題所占分值大多控制在15-22 分,題型一般為一個小題和一個大題、兩個小題和一個大題或者三個小題,但也有個別年份有所波動, 比如2017年文科卷I只考查兩個小題10 分,2019年文科卷III只查了一個大題12 分,I卷理科考查的很穩定,都是一小一大17 分;由上表不難發現,三角函數試題中選擇題和填空題有易有難,也經常出現在壓軸題的位置,解答題的考查一般穩定在解答題的第一題的位置,但2019年全國文理Ⅲ卷中解三角形的解答題放在解答題第二題的位置,說明全國卷解答題的考查順序存在一些不穩定的因素.

1.3 考查知識點全面

高考全國卷數學試題對“三角函數”內容考查比較全面,題型多樣,結構靈活,難度適中.重點考查三角函數的圖象與性質,三角恒等變換,解三角形等基礎知識的理解和應用,兼顧考查數學能力、數學思想方法以及數學核心素養.①對圖象與性質的考查主要出現在選擇題,包括三角函數圖象的變換、三角函數的最值問題、三角函數的周期性、單調性、對稱性等,著重考查學生的數學運算、直觀想象等核心素養以及數形結合思想.②對三角恒等變換的考查,選擇、填空、解答題都可能會出現,包括同角三角函數的關系式、誘導公式、兩角的和、差、倍角公式等基本概念、基本公式的理解與應用,在選擇題、填空題中該部分內容主要考查化簡求值,著重考查學生的數學運算核心素養以及轉化與化歸的能力.③對解三角形的考查,文科多在選擇、填空題中,主要考查利用三角恒等變換、正弦定理、余弦定理以及三角面積公式解三角形,理科在解答題中多數與三角恒等變換結合考查.④對三角函數與其他知識的綜合運用考查,比如2018年全國I卷理科第16 題,三角函數結合導數進行考查,難度較大,考查學生的邏輯推理、數學抽象、數學運算等數學核心素養以及化歸轉化、數形結合思想.

1.4 文理差異

由上表可以看出,全國卷文科考查三角函數試題24 道,題型基本穩定在三道小題,考查分值15 分,2019年全國文科Ⅲ卷僅考查了一道解答題,分值12 分,而理科考查23 道,基本穩定為一小一大,二小一大,少數年份三小,比如2018年II卷、2018年III卷、2019年II卷.全國I卷理科都穩定在一小一大,分值17 分.文理科的小題都有以壓軸題的形式出現,但理科考查的難度相比文科較大,考查內容綜合性強,常與函數零點、函數與導數相結合,對學生的數學運算、邏輯推理等核心素養以及化歸能能力要求比較高.

2 高考動向透視

研究歷年高考真題,力求以真題引領教學方向,通過對三年高考全國卷“三角函數”命題規律分析,三角函數高考試題主要考查以下幾種類型的問題.

2.1 三角函數恒等變換

三角函數恒等變換是歷年來高考的必考點,在選擇題、填空題、解答題中都會出現,主要考查三角函數式的化簡、求值與變形,但近年來對變形技巧的要求較往年大為降低.因此,在進行三角復習時,不能盲目地追求偏、難、怪的題目,而應利用中、低檔題熟練掌握一些基本的變形技巧.

題型一 化簡求值

化簡求值這類題型主要有三種,分別為給值求值、給角求值、給值求角,但三年都集中考查給值求值,即已知某些角的三角函數值, 求其他與題設條件關聯的其他三角函數值.給角求值以及給值求角在三年的全國卷高考三角函數試題中暫無涉及.

例1(2019 全國Ⅱ文11) 已知2 sin 2α=cos 2α+1,則( )

評析: 本題主要考查二倍角公式、同角三角函數的基本關系等知識,考查考生的運算求解能力與靈活應用所學知識分析問題、解決問題的能力,考查的數學運算核心素養.

答案: B

2.2 三角函數的圖象與性質

三角函數的圖象與性質在高考中出現的頻率較高,題型比較穩定,一般都是以選擇題的形式出現,其中,三角函數的性質偶爾會結合三角恒等變換以填空題形式出現.主要考查學生將函數解析式轉化為y=Asin(wx+φ)的形式,解答關于函數圖象及性質問題的能力.其高考命題形式主要包括以下4 種題型.

題型二 三角函數圖象變換

例2(2017 全國1 理9) 已知曲線C1:y= cosx,C2:y=則下面結論正確的是( )

A.把C1上各點的橫坐標伸長到原來的2 倍,縱坐標不變,再把得到的曲線向右平移個單位長度,得到曲線C2

B.把C1上各點的橫坐標伸長到原來的2 倍,縱坐標不變,再把得到的曲線向左平移個單位長度,得到曲線C2

C.把C1上各點的橫坐標縮短到原來的倍,縱坐標不變,再把得到的曲線向右平移個單位長度,得到曲線C2

D.把C1上各點的橫坐標縮短到原來的倍,縱坐標不變,再把得到的曲線向左平移個單位長度,得到曲線C2

評析: 本題考查圖象的變換,但題目出現了兩個異名的三角函數,處理這類問題的方法比較多,但主要是化異名為同名.破解此類題目關鍵是明晰圖象變換的規律,特別要注意的是先相位變換,后周期變換,再振幅變換或者是先周期變換,后相位變換,再振幅變換.

答案: D

題型三 三角函數的最值問題

三角函數最值問題對學生的化歸轉化能力、數形結合能力、綜合應用考查比較高, 更加深刻地考查學生的數學運算、邏輯推理、直觀想象等核心素養.破解此類問題有兩種途徑, 第一, 通過恒等變形再利用輔助角公式化為y=Asin(wx+φ)+b形式,再利用正弦函數的圖象,數形結合求出最值.第二,可以利用換元法把題設轉化為有區間的二次函數最值問題.

例3(2017 全國2 理14)函數的最大值是____.

評析: 本題主要考查三角函數的圖象和性質,換元法求最值,注意還原后新元的取值范圍,考查化歸與轉化思想與數學運算、邏輯推理核心素養.

答案: 1

題型四 已知解析式確定函數性質

給出三角函數的具體解析式, 求解函數的性質、參數或者確定函數的大致圖象, 此題主要在選擇、填空題中考查, 難度中等偏上, 破解此類問題的一般方法是通過恒等變形把題設的解析式轉化為y=Asin(wx+φ)+b或y=Acos(wx+φ)+b的形式, 然后根據y= sinx或y=cosx的性質整體求解.

例4(2018 全 國III卷理科15) 函數f(x) =在[0,π]的零點個數為____.

評析: 本此題考查了三角函數的零點,屬于三角函數的圖象和性質的常考點,這類問題通的處理方法是先得出問題的通解,再結合給定區間進行對照判斷.考查邏輯推理、直觀想象等核心素養.

答案: 3 個

題型五 根據條件確定解析式

根據條件確定解析式的試題主要有兩大類: 一類是題設給出三角函數的圖象,根據圖象確定及其已知條件確定三角函數的解析式,然后再求解其他性質;第二類是根據題設所給的三角函數性質求三角函數的解析式.這兩類問題是近三年全國卷三角函數考查的熱點,文科考查的難度較小,理科考查的難度較大,綜合考查學生邏輯推理、數學抽象、數學運算、直觀想象等核心素養.破解此類問題需要學生對函數y=Asin(wx+φ)+b或y=Acos(wx+φ)+b的圖象與性質有全面、深刻的理解,要求考生能夠根據零點與對稱軸信息,以及單調區間與周期的關系,通過數形結合得出該函數周期性特征,著重考查學生的數形結合能力、邏輯分析能力.

例5(2019 全國Ⅲ理12) 設函數f(x) = sin(ωx+已知f(x)在[0,2π]有且僅有5 個零點,下述四個結論:

①f(x)在(0,2π)有且僅有3 個極大值點; ②f(x)在(0,2π)有且僅有2 個極小值點; ③f(x)在單調遞增;④f(x)的取值范圍是其中所有正確結論的編號是( )

A.①④ B.②③ C.①②③ D.①③④

評析: 本題作為壓軸題,難度較大,主要考查三角函數的圖象與性質,考查考生的數形結合能力,更加深刻地考查學生數學抽象、直觀想象、邏輯推理等數學核心素養.

答案: D

2.3 解三角形

解三角形是三角函數內容的核心考點,歷年文理科高考全國卷必考內容,解三角形是歷年高考的必考內容,文科多在選擇、填空題中,主要考查利用三角恒等變換、正弦定理、余弦定理以及三角面積公式解三角形,理科在解答題中多數與三角恒等變換結合考查,題型和分值較為穩定,屬中等難度.命題方向由以下兩種.

題型六 正、余弦定理解三角形

在解有關三角形的形時,如果已知式子中含有角的余弦或邊的二次式,通常考慮用余弦定理;如果已知式子中含有角的正弦或邊的一次式,通常用正弦定理.

例6(2019 全國I文11)?ABC的內角A,B,C的對邊分別為a,b,c,已知asinA ?bsinB=4csinC,cosA=則=( )

A.6 B.5 C.4 D.3

評析: 本題主要考查正弦定理、余弦定理的應用,考查運算求解能力以及劃歸與轉化思想,考查數學運算,邏輯推理核心素養.

答案: A

題型七 正、余弦定理與三角恒等變換的綜合應用

求解此類問題的突破口: 一是正確分析已知條件中的邊角關系,合理設計“邊往角化”還是“角往邊化”,活用正弦定理、余弦定理;而是求角的值的值時應注意三角形對角的取值范圍的限制;三是熟記兩角和、差的三角公式.

例7(2019 全國I理17)?ABC的內角A,B,C的對邊分別為a,b,c,設(sinB ?sinC)2=sin2A ?sinBsinC.

(1)求A;

(2)若√+b=2c,求sinC.

評析: 本題主要考查正弦定理余弦定理、三角恒等變換,考查考生的劃歸與轉化能力、云算求解能力,考查的核心素養是數學運算,(1)利用正弦定理進行邊角互化,再利用余弦定理,即可求出cosA的值,從而求得A的大小;(2)利用正弦定理,將邊化為角,再利用(1)的結論以及兩角差的正弦公式與輔助角公式,即可求出sinC的值.

答案: (1)A=60°;(2)

題型八 三角函數與其他知識的綜合

例8(2018 全國一理16) 已知函數f(x) = 2 sinx+sin 2x,則f(x)的最小值是____.

評析: 本題主要考查導數與三角函數的結合交匯,借助導數的方法求函數的最值,體現導數的工具作用,本題難度較大,綜合考查學生化歸轉化能力、數形結合能力,考查邏輯推理、直觀想象、數學運算、數形抽象核心素養.

答案:

3 備考建議

3.1 利用好教材,研究教材中的例題與習題

以必修五第一章“解三角形”為例,教材中至少有如下一些例題、習題需要引起重視,教師要認真研究、分析到位.

人教版A 版第18 頁練習3: 三角形射影定理: 在?ABC中,求證:a=bcosC+ccosB,b=ccosA+acosC,c=acosB+bcosA.射影定理在2013年全國II卷第17 題,2016年全國II卷第17 題,2017年全國II卷第16 題均考查過.人教版A 版第20 頁B 組第1 題: 證明三角形面積公式2017年全國卷I理科第17 題考查過.

通過對比我們不難發現,近年高考中的三角命題多是通過課本習題的一個小結論發展演變而來,通過幾個公式環環相扣來提高問題的綜合性,這樣的命題方式讓學生入手容易,但完整解決整道題需要較高的數學素養水平.

3.2 樹立“模型”意識,統籌數學思想方法,“以不變應萬變”

比如課本20 頁A 組第13 題,考查三角形的中線長問題,這是解三角形中一個基礎但重要的模型.

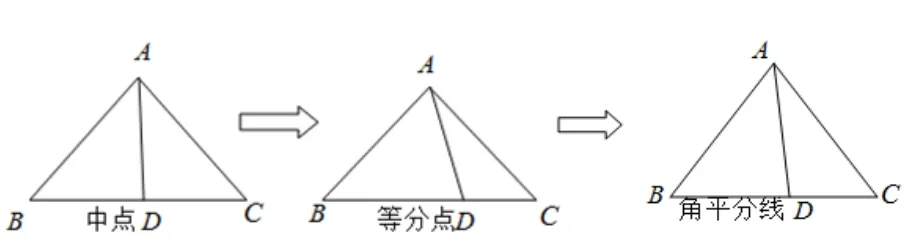
幾何圖象中有多個三角形時,首先觀察是否有“夠條件”的三角形,若有,則從夠條件的三角形解起,逐步擴展到其他三角形, 若沒有, 則要注意運用向量、方程的思想、利用“共邊”、“等角”、“互補角”等關系建立方程求解.模型是沒有背景的規律載體, 應該是具有通用性的大道理.老子說: 道生一,一生二,二生三,三生萬物.萬變不離其宗,大道歸一,大道至簡.

3.3 夯實基礎,總結方法

比如三角函數求最值：

(1)y=asinx+b,設t=sinx,化為一次函數y=at+b在[?1,1]上的最值求解.

(2)y=asinx+bcosx+c,引入輔助角化為求解方法同類型(1).

(3)y=asin2x+bsinx+c, 設t= sinx, 化為二次函數y=at2+bt+c在[?1,1] 上的最值求解, 也可以是y=acos2x+bsinx+c或y=acos 2x+bsinx+c型.

(4)y=asinxcosx+b(sinx±cosx)+c,設t=sinx±cosx, 則t2= 1±2 sinxcosx, 故sinxcosx=化為二次函數上的最值求解.

(5)y=,根據正弦函數的有界性,既可用分析法求最值,也可用不等式法求最值,更可以用數形結合求最值.

對于三角函數圖象變換問題, 首先要處理的是利用誘導公式將不同名函數轉換為同名函數, 轉換的公式為等誘導公式;另外,在進行圖象變換時,注意先有平移后伸縮和先伸縮后平移兩種,后者在考試中經常出現,但無論哪種變換,要讓學生明確每一個變換總是對變量而言,與其他量無關.

3.4 夯實基礎,注重規范大題

熟記與三角函數相關所有公式.如特殊角的三角函數值、誘導公式、恒等變換公式還有正余弦定理、三角形面積公式,同時還包括三角函數圖象平移規律,特殊三角形的邊角關系等,只有記得準和反映迅速,才能在考試中快速及時的運用相關已知條件;三角函數若考查解答題,則大多在第17題的位置,對解題的規范性要求很高,因此要培養學生規范答題的良好習慣,同時,又因為這是試卷中的第一道大題,因此難度不大,所以更要注重通性通法,做到滿分無瑕疵.