排氣系統吊鉤位置優化分析*

鄂世國，李京福，徐小彬

排氣系統吊鉤位置優化分析*

鄂世國，李京福，徐小彬

（華晨汽車工程研究院，遼寧 沈陽 110141）

排氣系統吊鉤與車身相連，它的振動對車身的有著明顯的激勵作用。文章通過有限元方法建立排氣系統模態模型，賦予發動機及懸置，橡膠吊耳等參數。基于MSC.Nastran進行模態求解，計算出從0-200Hz模態結果，驗證排氣系統的模態與怠速頻率避頻。通過平均驅動自由度位移（ADDOFD）法，找出合理的排氣系統各個吊點的布置位置。

平均驅動自由度位移法；排氣系統模態；排氣系統吊點布置

前言

排氣系統作為車輛的激勵源之一，尤其在加速過程中逐漸成為振動、噪聲主要來源之一，同時也成為了汽車NVH界廣泛關注的焦點[1]。當發動機加速過程中，排氣系統會產生劇烈的振動，嚴重影響了排氣吊點的耐久性，并且激勵力可經過吊鉤支架傳遞至車身側，嚴重影響了車輛結構的NVH性能，因此排氣系統的模態必須與發動機的激振頻率及車身的模態分開，否則系統耦合在一起會產生強烈的共振。利用有限元方法對排氣系統進行振動及模態分析，在整車開發早期能夠對排氣吊耳進行合理化布置，有效的提高了車輛的NVH性能。

1 排氣系統的模態分析

1.1 模態分析

模態分析是將線性時不變的系統振動微分方程組中的物理坐標轉換為模態坐標，使方程組解耦，成為一組以模態坐標及模態參數描述的獨立方程，坐標變換的變換矩陣為振型矩陣，其每列即為各階振型。此線性系統在原來的物理坐標中，對任何激振的響應，可以看作是此系統每階固有的振型按照特定的比例疊加而成的結果。在這個振動系統中，動力微分方程[2]為：

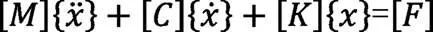
式中F為載荷向量，X是位移向量[M]，[C]，[K]分別為系統的質量、阻尼和剛度陣。對于結構的模態特性，可以通過某組模態的參量來表達。模態的參量主要是模態振型和固有頻率。由于外界的激勵施加的大小并不會影到固有頻率，當結構阻尼很小時，那么固有頻率幾乎不受任何影響，可以忽略不計，因此便可以利用無阻尼計算，來求解線性系統的模態的參量。式（1）可知：

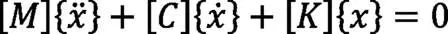
當上式的解為=?e，可將其代入（2）式中求解齊次方程（3）：

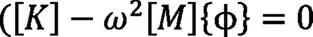
當（2）式中的特征方程等于零時，方能確定非零解的存在，即：

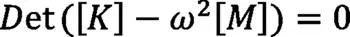
基于數學理論公式，N個共振頻率的存在會對應N個自由度的系統。

ω（j= 1,2, ……, N）。每個模態振型便是固有頻率對應的特征向量。模態振型也對應著結構撓度，它體現了結構根據頻率振動后每個自由度振幅的占比。排氣系統的結構模態參量反映出結構固有的振動屬性，同時排氣系統的結構的振動對車身的激勵起著至關重要的作用。排氣系統模態在設計過程中應當盡量對問題大的振動頻率ω與路面及動力總成激勵頻率避開。

1.2 排氣系統有限元模型的建立

汽車排氣系統通常主要包括法蘭盤、催化器、波紋管、消音器、吊鉤、橡膠吊耳、主管和尾管。研究排氣系統振動特性的主要工作是建立準確的有限元模型。對于排氣系統結構很復雜的情況，要建立有限元模型就需要進行適當的簡化。如圖1所示。

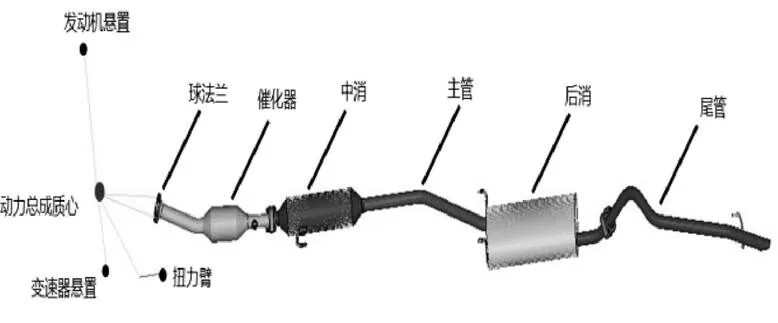
圖1 排氣系統模態模型

表1 吊耳剛度

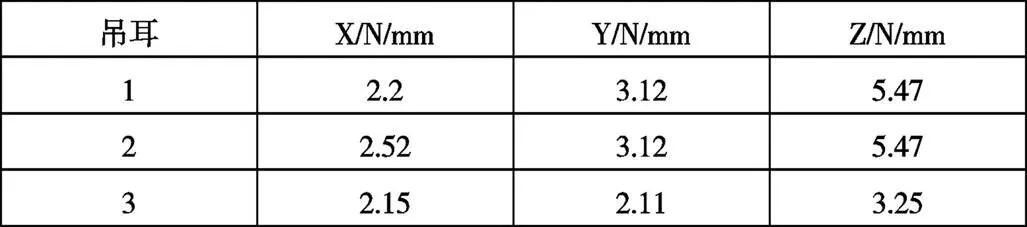
汽車排氣系統的模態仿真模型主要為殼單元，前后消和管體，網格尺寸5x5mm，法蘭盤和吊鉤為實體單元；波紋管和橡膠吊耳均采用彈簧CBUSH單元加以簡化，但需保證波紋管的長度、質量及剛度。發動機采用剛性單元RBE2，發動機質心處添加實際質量和轉動慣量。發動機，變速器與車身懸置連接采用彈簧CBUSH單元模擬，給予真實的剛度值。排氣吊鉤處的橡膠吊耳采用彈簧CBUSH單元模擬并給予真實的剛度值，如表1所示。

2 排氣系統模態計算

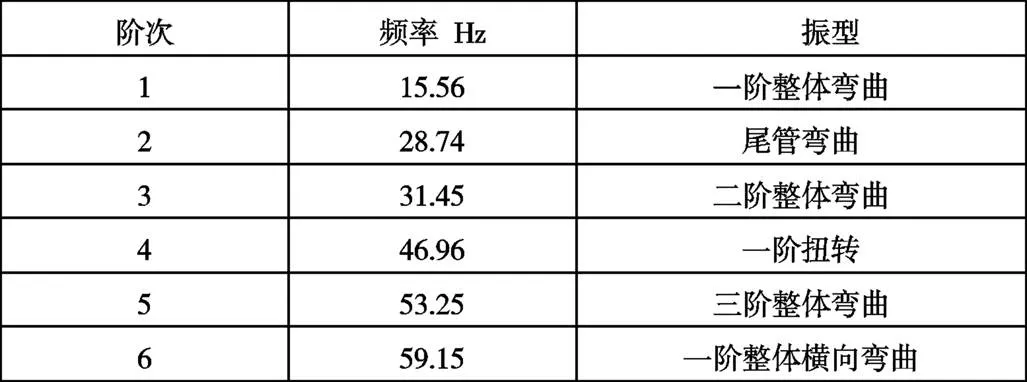
汽車怠速轉數一般為750rpm，對于四缸發動機換算成二階點火頻率為25Hz，排氣系統在真實約束條件下進行模態分析，結果需要與25Hz進行避頻，避頻頻率大于3Hz。本系統結果滿足設計要求。通過蘭索斯求模態法，計算出排氣系統前20階模態值，如表2及圖2所示。

表2 排氣系統模態振型

3 排氣系統吊鉤位置優化分析

3.1 平均驅動自由度位移（ADDOFD）法

利用模態理論，基于多個自由度的線性系統，當為單點激勵時，則作為系統激勵點p和響應點的l的頻響相關函數[3]為：

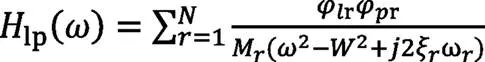
如上式中，φ是第r階的模態系數，第l個采樣點；M和ξ分別是系統的質量矩陣與模態阻尼比。當激勵頻率為ω，則有相似：

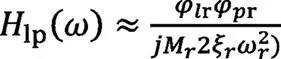
為線性系統，則那么頻響幅值與位移幅值成正比，即：

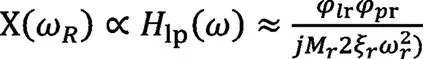
當對模態振型進行質量歸一，各階模態阻尼基本保持一致，即：

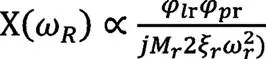
那么第j個平均自由度位移（ADDOFD）如下：

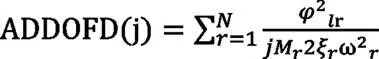
ADDOFD（j）能夠計算出某自由度在某激勵下的對應響應位移，而且利用此位移響應可以進行排氣系統吊鉤位置的最優化布置。

3.2 排氣吊點優化布置

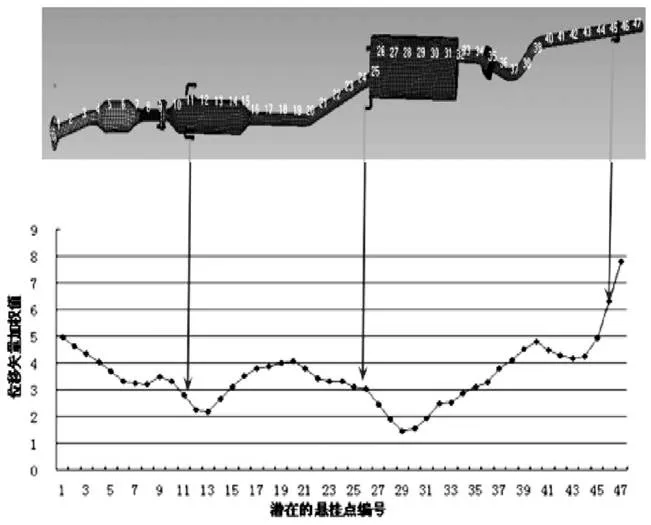
圖3 排氣吊鉤位置選取

在前處理軟件中對排氣系統的排氣歧管位置到尾管末端，每隔10mm進行選取并對其進行編號。通過后處理軟件將排氣系統各節點按照編號順序，將排氣系統從0到200Hz的各階次模態輸出，根據平均驅動自由度位移（ADDOFD）法，對各點進行平均計算。吊鉤位置合理處應該選取在曲線的波谷處，此處的系統抖動的位移較小。如圖3所示。

4 結語

本文通過前處理軟件對排氣系統的模態模型進行搭建，并計算出對應的模態頻率和模態振型。并通過計算驗證是否滿足設計要求。最后通過平均驅動自由度位移法對吊鉤位置進行合理的選取，找出最優位置。此方法節約了開發成本與開發周期，并為后期排氣系統NVH性能的控制奠定了基礎。

[1] 龐劍.諶剛,何華.汽車噪聲與振動理論與應用[M].北京:北京理工大學出版社,2006.

[2] 田麗思.MSC.Nastran動力分析指南[M].北京:中國水利水電出版社,2012.

[3] 傅志方,華宏星.模態分析理論與應用[M].上海:上海交通大學出版社,2000.

Automobile exhaust system hook location optimization*

E Shiguo, Li Jingfu, Xu Xiaobin

（Brilliance Automobile Engineering Research Institute, Liaoning Shenyang 110141）

Automobile exhaust system hook is connected with BIW. The hook will excite the BIW vibrating forcefully. The automobile exhaust system is established by FEA method. The engine, its suspension and damping rubber are provided. By MSC.Nastran, the modal is calculated. The range of modal frequency result is from 0 to 200Hz. It has proved that it is different between the modal frequency and idle frequency. By the ADDOFD method, it found out the reasonable position.

ADDOFD method;Exhaust system moda;Exhaust system hooks arrangement

10.16638/j.cnki.1671-7988.2021.02.025

U467

A

1671-7988(2021)02-78-03

U467

A

1671-7988(2021)02-78-03

鄂世國，碩士學位，中級工程師，就職于華晨汽車工程研究院，從事整車CAE仿真分析工作。