2020年高考全國(guó)Ⅲ卷理科第21題的探析

廣東省佛山市樂(lè)從中學(xué)(528315) 林國(guó)紅

一、題目呈現(xiàn)與分析

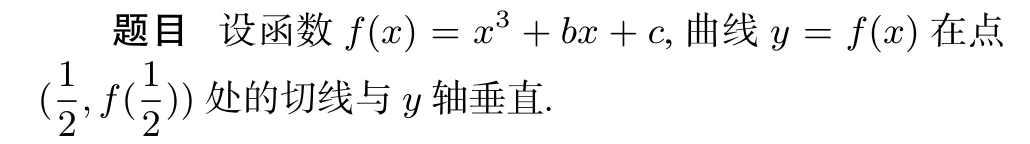
(1)求b;

(2)若f(x)有一個(gè)絕對(duì)值不大于1 的零點(diǎn),證明:f(x)所有零點(diǎn)的絕對(duì)值都不大于1.

試題分析題目結(jié)構(gòu)非常簡(jiǎn)單,是以三次函數(shù)為背景的函數(shù)導(dǎo)數(shù)題.知識(shí)方面主要考查導(dǎo)數(shù)的運(yùn)算,函數(shù)的切線方程,函數(shù)零點(diǎn)的相關(guān)問(wèn)題等;思想方面主要考查分類(lèi)討論,轉(zhuǎn)化與化歸,方程與函數(shù)等思想.綜合考查考生對(duì)函數(shù)、方程、導(dǎo)數(shù)、不等式等基礎(chǔ)知識(shí)的掌握和理解,邏輯思維轉(zhuǎn)化、推理論證及運(yùn)算等方面的能力.

試題分步設(shè)問(wèn),逐步推進(jìn),由淺入深,重點(diǎn)突出,較好地達(dá)到了考查目的.試題第(1)問(wèn)的設(shè)計(jì)面向大部分考生,考生只要能理解切線的含義,準(zhǔn)確應(yīng)用導(dǎo)數(shù)運(yùn)算法則就可以解決問(wèn)題.試題第(2)問(wèn)是零點(diǎn)有關(guān)的證明題,試題的設(shè)置為考生的解答提供廣闊的想象空間,對(duì)于考生運(yùn)用所學(xué)知識(shí),尋找合理的解題策略以及推理論證能力有較高的要求.本題層次分明,區(qū)分度高,是一道能突出選拔學(xué)生功能的好題.

由于問(wèn)題(1)較為簡(jiǎn)單,本文不作討論,下面從不同視角,給出問(wèn)題(2)的幾種證法,拋磚引玉.

二、解法探析

1 視角一:利用零點(diǎn)存在性定理

評(píng)注“函數(shù)零點(diǎn)的存在性定理”在零點(diǎn)問(wèn)題中應(yīng)用廣泛,一般來(lái)說(shuō):要求證一個(gè)函數(shù)“有且只有一個(gè)”零點(diǎn),可先用“函數(shù)零點(diǎn)的存在性定理”證明函數(shù)存在零點(diǎn);再證明函數(shù)為單調(diào)函數(shù),即得函數(shù)零點(diǎn)的唯一性.其依據(jù)為:如果函數(shù)f(x)在區(qū)間[a,b]上是單調(diào)函數(shù),并且f(a)·f(b)＜0,則函數(shù)f(x)在區(qū)間(a,b)上至多有一個(gè)零點(diǎn).如果要證明函數(shù)有多個(gè)零點(diǎn),一般要將區(qū)間分隔討論解決.兩個(gè)證法涉及函數(shù)的單調(diào)性、函數(shù)的零點(diǎn)等多個(gè)知識(shí)點(diǎn),綜合考查函數(shù)與方程的思想、轉(zhuǎn)化與化歸,分類(lèi)討論等思想,其中證法2 用到了反證法.

2 視角二:利用參數(shù)c 的范圍

有零點(diǎn)的絕對(duì)值都不大于1.

綜上,若f(x)有一個(gè)絕對(duì)值不大于1 的零點(diǎn),則f(x)所有零點(diǎn)的絕對(duì)值都不大于1.

評(píng)注證法3 與證法4 利用已知條件“f(x)有一個(gè)絕對(duì)值不大于1 的零點(diǎn)”求得參數(shù)c 的范圍,再通過(guò)c 的范圍來(lái)證明其它零點(diǎn)的絕對(duì)值都不大于1.兩種證法比證法1 與證法2 減少了分類(lèi)討論的步驟,解答過(guò)程更簡(jiǎn)捷,其中證法4 利用“三角換元”及三倍角公式,方法更巧妙.兩個(gè)證法的難點(diǎn)在于三次不等組的求解.

3 視角三:利用二次函數(shù)或二次方程

綜上,若f(x)有一個(gè)絕對(duì)值不大于1 的零點(diǎn),則f(x)所有零點(diǎn)的絕對(duì)值都不大于1.

不等式(2t±1)2≥0 顯然成立,從而f(x)所有零點(diǎn)的絕對(duì)值都不大于1.

綜上,若f(x)有一個(gè)絕對(duì)值不大于1 的零點(diǎn),則f(x)所有零點(diǎn)的絕對(duì)值都不大于1.

評(píng)注兩個(gè)證法都要將三次多項(xiàng)式進(jìn)行因式分解,這也是證法的難點(diǎn).其中證法5 因式分解后利用二次函數(shù)的相關(guān)性質(zhì)進(jìn)行證明,證法6 因式分解后利用二次方程及不等式進(jìn)行證明,兩個(gè)證法都不涉及到導(dǎo)數(shù)的有關(guān)知識(shí).

4 視角四:利用不等式

綜上,若f(x)有一個(gè)絕對(duì)值不大于1 的零點(diǎn),則f(x)所有零點(diǎn)的絕對(duì)值都不大于1.

評(píng)注證法7 利用均值不等式證明結(jié)論,證法8 利用柯西不等式證明結(jié)論,兩個(gè)證法都不涉及到導(dǎo)數(shù)的有關(guān)知識(shí),證明思路新穎巧妙.

三、解后小結(jié)

以上的幾種證法,從不同的角度出發(fā)思考問(wèn)題,各顯神通.這充分體現(xiàn)數(shù)學(xué)高考題的不拘一格,一道試題往往考查多種能力、多種思想方法;同時(shí),高考試題在命制時(shí)充分考慮到考生數(shù)學(xué)能力的個(gè)體差異,多數(shù)試題的解答方法、思維方式不是唯一,一題多解,給考生提供了較大的發(fā)揮空間.這樣通過(guò)方法的選擇、解題時(shí)間的長(zhǎng)短,甄別出考生能力的差異,達(dá)到精確區(qū)分考生的目的.

從不同的思維角度分析同一道題目,得到不同的解題方法,一題多解的方式增加了題目涉及的知識(shí)廣度,以一帶多,減少了考查同樣多的知識(shí)所需的題量.從數(shù)學(xué)知識(shí)的角度來(lái)看,通過(guò)解題發(fā)現(xiàn)知識(shí)的相互聯(lián)系,體會(huì)知識(shí)之間的轉(zhuǎn)化過(guò)程,從多角度地思考和發(fā)現(xiàn)問(wèn)題,構(gòu)建知識(shí)網(wǎng)絡(luò)體系.這樣,在學(xué)習(xí)基礎(chǔ)知識(shí)、掌握基本技能的同時(shí),能培養(yǎng)學(xué)生思維的廣闊性、深刻性、靈活性以及創(chuàng)新性,能夠使學(xué)生對(duì)學(xué)習(xí)的內(nèi)容有一個(gè)整體的認(rèn)識(shí),并將知識(shí)融會(huì)貫通,舉一反三,開(kāi)闊眼界,活躍思維,從而提煉出數(shù)學(xué)思想與方法,這正是數(shù)學(xué)教學(xué)的核心.

四、試題的背景探析

1 余弦的多倍角公式

我們知道cos(nθ)可以表示成關(guān)于cosθ 的多項(xiàng)式:cos(0)=1,cos(x)=cos x,cos(2x)=2cos2x - 1,cos(3x)=4cos3x-3 cos x,cos(4x)=8cos4x-8cos2x+1,cos(5x)=16cos5x-20cos3x+5 cos x,···.

2 切比雪夫多項(xiàng)式

記Tn(x)=cos(n·arccos x),則Tn(x)是一個(gè)n 次多項(xiàng)式,稱(chēng)為n 次切比雪夫多項(xiàng)式,其中x ∈[-1,1],n ∈N.于是T0(x)=1,T1(x)=x,T2(x)=2x2-1,T3(x)=4x3-3x,T4(x)=8x4-8x2+1,T5(x)=16x5-20x3+5x,···.切比雪夫多項(xiàng)式有許多良好的性質(zhì),例如:

性質(zhì)1Tn(cos θ)=cos(nθ),θ ∈R,n ∈N.

性質(zhì)2當(dāng)|x|≤1 時(shí),|Tn(x)|≤1,x ∈R.

性質(zhì)3函數(shù)列{Tn(x)}滿足二階遞推關(guān)系Tn+2(x)=2xTn+1(x)-Tn(x).

由證法4,可以發(fā)現(xiàn)試題與余弦的三倍角公式有關(guān).事實(shí)上,這正是試題的命題背景:切比雪夫多項(xiàng)式的性質(zhì)1 與性質(zhì)2 的綜合應(yīng)用,即當(dāng)n=3 時(shí),若|x| ≤1,當(dāng)且僅當(dāng)|4x3-3x|≤1.

切比雪夫多項(xiàng)式是高等數(shù)學(xué)的內(nèi)容,它的相關(guān)結(jié)論有著廣泛的應(yīng)用,將其“鑲嵌”在高考題中可謂獨(dú)具匠心,命題者借助具有高等數(shù)學(xué)背景的試題來(lái)考查學(xué)生對(duì)知識(shí)的掌握程度和繼續(xù)學(xué)習(xí)的潛力,雖然試題的立意是“高等”的,但解法是“初等”的,不會(huì)在解答時(shí)對(duì)考生造成思維障礙,考生只要具備靈活運(yùn)用高中數(shù)學(xué)知識(shí)的相關(guān)的能力就能完成解答.這正好契合了新課程標(biāo)準(zhǔn)的要求:獲得必要的數(shù)學(xué)基礎(chǔ)知識(shí)和基本技能,理解基本的數(shù)學(xué)概念、數(shù)學(xué)結(jié)論的本質(zhì),了解概念、結(jié)論等產(chǎn)生的背景與應(yīng)用,體會(huì)其中所蘊(yùn)含的數(shù)學(xué)思想和方法以及它們?cè)诤罄m(xù)學(xué)習(xí)中的作用.

近年來(lái),高考的命題者通過(guò)挖掘高等數(shù)學(xué)中的一些素材來(lái)命制高考試題,此類(lèi)試題也逐漸引起老師們的關(guān)注.但這并不意味著要將過(guò)多的高等數(shù)學(xué)知識(shí)下放到中學(xué)里來(lái),加重中學(xué)的負(fù)擔(dān),應(yīng)該是教師能站在高觀點(diǎn)的角度看待問(wèn)題,找到問(wèn)題的本質(zhì)內(nèi)涵,更好地指導(dǎo)中學(xué)的數(shù)學(xué)教學(xué).