分而視之,思廣則域寬
——2020年高考全國I卷理科第21題一題多解與備考策略

佛山市南海石門中學(528248) 劉依舒

教育部考試中心提出的“一核四層四翼”高考評價體系中的“四層”明確表示,“關鍵能力”和“學科素養”的考查,要把握兩個字,“思”和“廣”.思,就是對每一道試題,要多想:考查知識是什么? 解答思路有幾個? 同類試題見過沒? 答案組織順暢嗎? 廣,就是廣泛涉獵學科相關內容:除了教材、各種優質試題,還有相關讀物,學科領域最新進展.函數導數一向是考生棘手的問題,如何令考生有步驟可寫,有分可拿,是眾多一線教師矚目的問題.本文對2020年高考全國I 卷理科第21 題的解法進行分析,結合考試大綱與新高考的動向,參考一輪復習資料的習題,提出函數恒成立求參數取值范圍問題的備考策略.

一、提出問題

二、解法分析

(一)構造函數法

(二)端點效應

圖1

端點效應有時候還需要二階導去判斷凹凸性,這一部分內容課本上并沒有涉及,出題人并不希望學生使用“高觀點”的做法去解題(如洛必達法則等),對學生要求高,這些都不利于提升學生的數學核心素養.而且這也不是解決該類問題的通性通法,在一輪復習中可以引用,但不值得大力提倡.于是,我們引用“分離參數法”對該題進行研究.

(三)分離參數法

(四)數形結合法

圖2

該種解法中,本質上還是分離參數,由于直線性質較曲線性質易于研究,我們讓參數留在一次函數中,達到“定曲動直”的效果.且這樣的分離,這個函數的性質易于研究.

上述提到2017年全國Ⅱ卷函數導數題可以用端點效應解決,筆者也試了下數形結合的方法,如下:

例1(2017年高考全國Ⅱ卷)設函數f(x)=(1-x2)ex.當x ≥0 時,f(x)≤ax+1,求a 的取值范圍.

解f(x)圖像如圖3所示.y=ax+1 為過(0,1)的直線,要當x ≥0 時使得f(x)≤ax+1恒成立,只需把相切的臨界斜率a0求出來,a ≥ a0即可.f(0)=1,即y=ax+1 與f(x)在(0,1)相切即可.f′(x)=(1-2x-x2)ex,a0=f′(0)=1.所以a ≥1.

圖3

后續還要有嚴密的代數推理否定a ＜1,但由此看來,這種解法大大節省了考生計算的時間,降低了解題的難度.也不比端點效應法來得困難.

筆者在對學生一輪復習資料進行研究后發現,對函數恒成立求參數取值范圍的題目大部分都可以使用上述的數形結合的辦法進行解決,下面引用兩例說明:

例2(2020年石家莊市高三一檢)已知函數f(x)=axex-(a+1)(2x-1).第二問:當x＞0 時,函數f(x)≥0恒成立,求實數a 的取值范圍.

解 當x=1 時,f(1)=ae-(a+1)(2-1)≥0 恒成立,把一個x 值代入,先把a 的范圍縮小,方便后面的式子變形.)

f(x)可變形為 xex≥為過定點的直線.要使曲線h(x)恒在直線g(x)的上方,只需把相切的臨界斜率求出來,即可.解得.

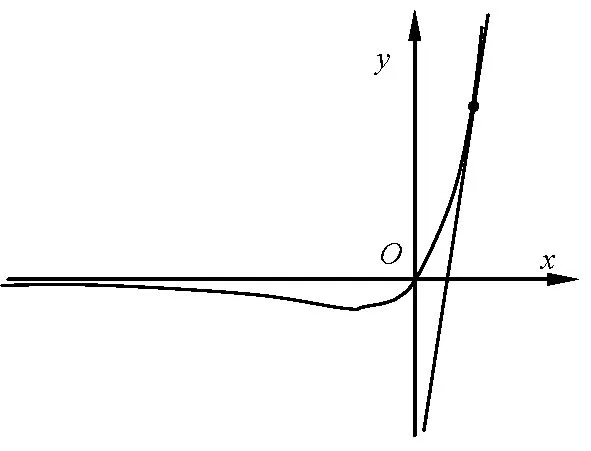
圖4

例3已知函數第二問:若函數f(x)在上無零點,求a 的取值范圍.

解f(x)在上無零點等價于2 ln x=0 在上無實根,也等價于h(x)與g(x)在上無交點,其中h(x)=(2-a)(x-1),g(x)=2 ln x.h(x)是過定點(1,0),斜率為k=(2-a)的直線,g(x)是確定的曲線.

圖5

三、總結提升

羅增儒教授在《數學解題關鍵環節的確定與教學設計》[2]中指出,數學教師必須具備將解題能力轉化為他的教學能力,對此,他需要特別關注學生發生數學問題思路的某些關鍵環節時學生的心理環節及其過渡性中介生成,從而設計教學過程循循善誘,引導學生依靠自己的認知結構的力量,重新萌生這種思路的關鍵環節.所以筆者認為,在一輪復習中滲透函數導數的做題思想與方法非常重要,不能就題論題,我們應當通過教學活動幫助學生學會思考,面對函數導數題,在深入審題的基礎上,必要時可回歸基本初等函數及其簡單組合的常見函數,將較為復雜的函數分而視之,指導學生直觀思想立意要領,運用思想引領方法,讓數學問題變得可視化,“橫看成嶺側成峰,遠近高低各不同”,站在更寬廣的領域思考問題,方能達到更高的境界.