熔融物堆內(nèi)滯留條件下RPV長(zhǎng)期結(jié)構(gòu)完整性分析
高永建,賀寅彪,曹 明
(上海核工程研究設(shè)計(jì)院有限公司,上海 200233)
自1976年三哩島核電廠發(fā)生堆芯熔化事故以來(lái),對(duì)于該類嚴(yán)重事故的安全分析及相關(guān)事故應(yīng)對(duì)策略的研究一直是核能領(lǐng)域的研究重點(diǎn)[1-2]。通過(guò)反應(yīng)堆壓力容器(RPV)外部水冷實(shí)現(xiàn)堆芯熔融物RPV內(nèi)滯留(IVR)是三代核電廠重要的嚴(yán)重事故緩解措施之一,這一措施可有效防止RPV發(fā)生失效,進(jìn)而限制RPV外的嚴(yán)重事故(如RPV外蒸汽爆炸、堆芯熔融物-混凝土相互作用等)的發(fā)生,以保證安全殼的結(jié)構(gòu)完整性。
實(shí)現(xiàn)IVR策略的關(guān)鍵是保證RPV的結(jié)構(gòu)完整性,IVR條件下RPV的失效模式分為兩類:熱工失效和結(jié)構(gòu)失效[3]。防止熱工失效的條件是熔融物傳向容器壁的熱流密度始終小于臨界熱流密度(CHF),使得RPV外壁面始終處于核態(tài)沸騰狀態(tài);防止結(jié)構(gòu)失效是研究RPV結(jié)構(gòu)在高溫和高溫差應(yīng)力聯(lián)合作用下的蠕變、斷裂等強(qiáng)度問(wèn)題。前者是后者的必要條件。
值得注意的是,日本福島核電廠事故中,在由于廠外失電和堆芯冷卻系統(tǒng)功能喪失使得堆芯無(wú)法被有效冷卻導(dǎo)致其最終熔化的同時(shí),RPV內(nèi)部壓力長(zhǎng)時(shí)不能釋放[4],同時(shí),三代核電廠的嚴(yán)重事故管理導(dǎo)則(SAMG)中還會(huì)考慮堆內(nèi)注水,進(jìn)而也會(huì)引入一定的內(nèi)壓,因此開(kāi)展考慮內(nèi)壓的IVR條件下RPV結(jié)構(gòu)完整性研究是有必要的。本文將就此展開(kāi)分析與探討。
1 分析與評(píng)價(jià)方法
RPV結(jié)構(gòu)在IVR條件下存在發(fā)生蠕變斷裂的可能性,本質(zhì)上這是由蠕變損傷引起的材料斷裂引起的。由于材料的蠕變損傷是一個(gè)時(shí)間相關(guān)問(wèn)題,且蠕變應(yīng)變會(huì)隨著時(shí)間不斷發(fā)生變化,因此,首先需計(jì)算得到不同時(shí)刻下結(jié)構(gòu)的應(yīng)力應(yīng)變響應(yīng),在此基礎(chǔ)上進(jìn)行蠕變損傷計(jì)算與評(píng)價(jià),評(píng)價(jià)流程示于圖1。
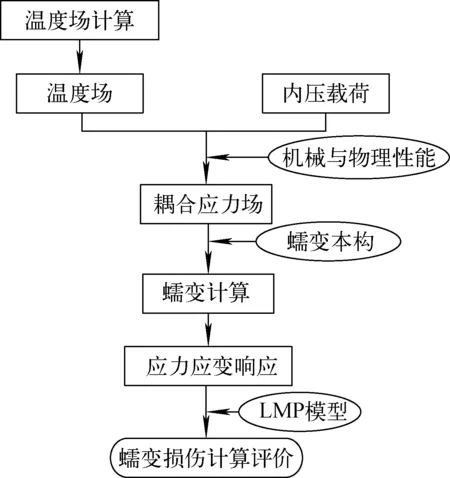
圖1 評(píng)價(jià)流程圖Fig.1 Evaluation flow chart
本文的蠕變損傷計(jì)算使用基于Larson-Miller參數(shù)(LMP)的累積損傷理論,LMP和斷裂時(shí)間tr(h)之間的關(guān)系[5]為:
LMP=0.001(20.0+lgtr)T
(1)
由式(1)變換后,可得tr的表達(dá)式:
(2)
通過(guò)數(shù)據(jù)擬合,給出初始施加應(yīng)力σ0(MPa)與LMP的擬合關(guān)系[3]:
(3)
對(duì)于給定應(yīng)力σ和溫度T下,Δt時(shí)間內(nèi)結(jié)構(gòu)的損傷增量ΔD可定義為:
(4)
通過(guò)損傷增量的累積分析獲得給定時(shí)間下總的結(jié)構(gòu)損傷:
(5)
當(dāng)D≥1時(shí),材料將發(fā)生蠕變斷裂。
需要注意的是,LMP是基于單軸恒載(拉伸)蠕變數(shù)據(jù)確定的,而實(shí)際結(jié)構(gòu)處于多軸應(yīng)力狀態(tài),若用Von-Mises等效應(yīng)力來(lái)表征應(yīng)力狀態(tài)是不合理的,因?yàn)樗鼰o(wú)法區(qū)分拉伸和壓縮,同時(shí),若用最大主應(yīng)力來(lái)表征應(yīng)力狀態(tài)也是不可行的,因?yàn)樗姆较螂S時(shí)間發(fā)生改變。Huddleston[6]較好地解決了這一問(wèn)題,他提出了多軸蠕變斷裂強(qiáng)度模型,其對(duì)等效應(yīng)力σe給出定義:
(6)
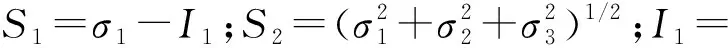
Huddleston發(fā)現(xiàn)系數(shù)a介于0.85~1.1,且1.0適用于大多數(shù)場(chǎng)合;系數(shù)b介于0.15~0.3,且0.24是推薦值。應(yīng)用以上a、b系數(shù)的推薦值,式(6)可簡(jiǎn)化為:
σe=σoee0.24(I1/S2-1)
(7)
2 載荷與材料性能
2.1 載荷
通過(guò)計(jì)算流體力學(xué)(CFD)分析獲得RPV在IVR條件下的溫度邊界,可發(fā)現(xiàn),容器壁厚方向上承受高溫度梯度載荷。本文分析時(shí)假定與熔池接觸的內(nèi)壁面溫度為RPV用鋼的熔點(diǎn)(1 327 ℃),高于熔池的內(nèi)壁面溫度隨高度呈迅速遞減;外壁面溫度假定為水的核狀沸騰溫度130 ℃。另外,RPV的內(nèi)外氣壓差假定為0.1 MPa。
2.2 材料性能
1) 機(jī)械與物理性能
鑒于SA-508 Gr.3 Cl.1的試驗(yàn)數(shù)據(jù)有所不足,并考慮到SA-533 B Cl.1的材料性能與SA-508 Gr.3 Cl.1較為接近,本文使用SA-533 B Cl.1的材料性能作為分析輸入。通過(guò)查詢文獻(xiàn)[7-10]得到SA-533 B Cl.1的屈服強(qiáng)度、楊氏模量、密度、熱傳導(dǎo)率和線膨脹系數(shù)隨溫度的變化關(guān)系,圖2示出了屈服強(qiáng)度Sy隨溫度T的變化(限于篇幅,其余參數(shù)從略)。
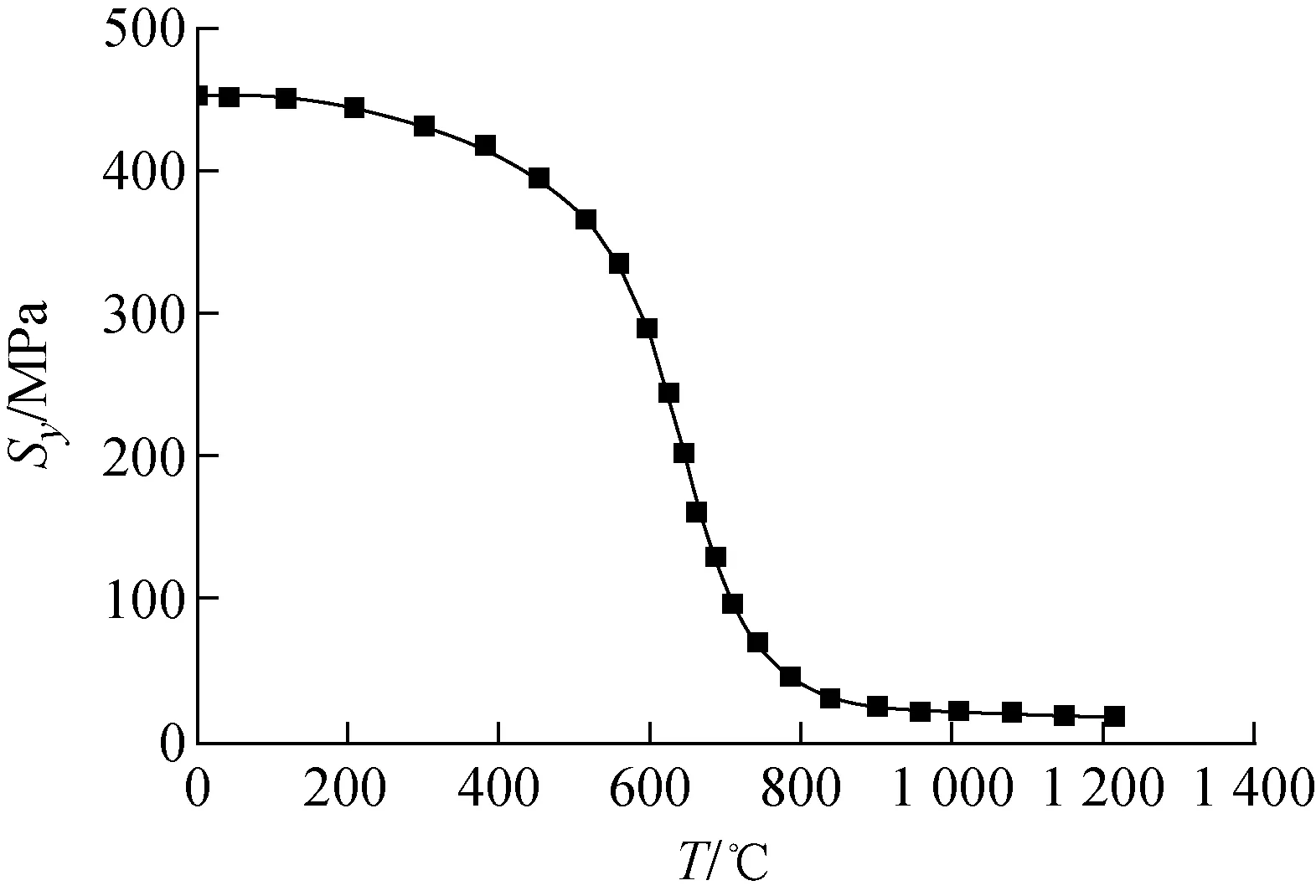
圖2 屈服強(qiáng)度隨溫度的變化Fig.2 Relationship between yield stress and temperature
2) 蠕變本構(gòu)
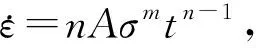

表1 蠕變本構(gòu)方程Table 1 Creep constitutive model
3) 蠕變持久試驗(yàn)數(shù)據(jù)
SA-533 B Cl.1的蠕變持久試驗(yàn)數(shù)據(jù)來(lái)源于INEL[3],其完成了溫度介于627~1 100 ℃的蠕變持久試驗(yàn),其試驗(yàn)數(shù)據(jù)列于表2。
3 分析與討論
3.1 有限元模型及邊界條件
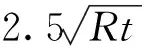
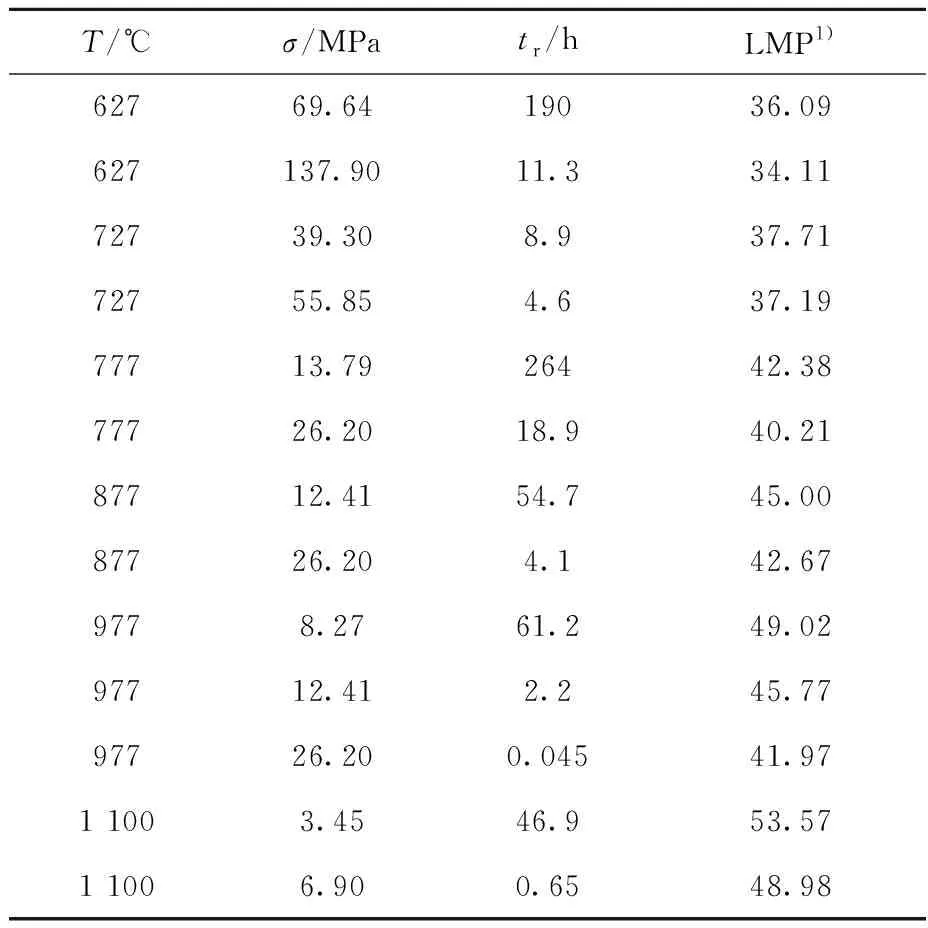
表2 蠕變持久試驗(yàn)數(shù)據(jù)Table 2 Creep-rupture test data
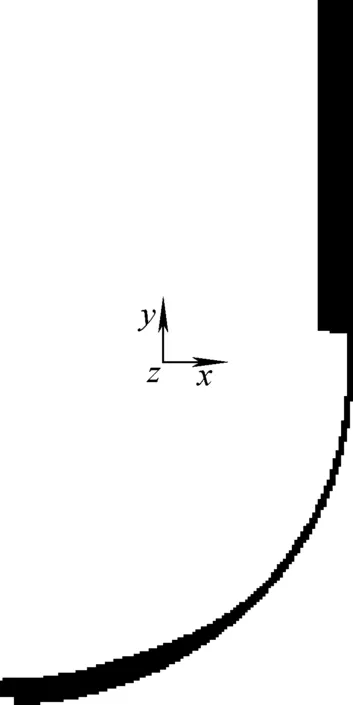
圖3 IVR條件下RPV網(wǎng)格模型Fig.3 Finite element model used in simulation
對(duì)于熱分析,根據(jù)2.1節(jié)給出的溫度邊界,在有限元模型對(duì)應(yīng)邊界施加相應(yīng)的溫度載荷;對(duì)于初始應(yīng)力(0 s時(shí)刻)計(jì)算,將熱分析得到的溫度場(chǎng)文件讀入,并在內(nèi)壁面施加內(nèi)壓載荷0.1 MPa;對(duì)于蠕變計(jì)算,將初始應(yīng)力計(jì)算得到的應(yīng)力場(chǎng)讀入,并根據(jù)表1定義不同溫度下(共定義了10個(gè)溫度點(diǎn))的蠕變本構(gòu)關(guān)系,并將蠕變效應(yīng)打開(kāi)。應(yīng)力/蠕變分析時(shí)在筒體段上端面做軸向位移約束。
3.2 蠕變損傷評(píng)價(jià)
通過(guò)蠕變計(jì)算,得到了不同時(shí)刻下的應(yīng)力應(yīng)變分布,在此基礎(chǔ)上首先利用蠕變斷裂模型進(jìn)行蠕變損傷計(jì)算,考查結(jié)構(gòu)發(fā)生局部蠕變斷裂的可能性;其次,通過(guò)觀察厚度方向上的環(huán)向應(yīng)力、子午線向/軸向應(yīng)力(徑向應(yīng)力可忽略,因?yàn)閳A柱殼/球殼在內(nèi)壓/溫度載荷下的徑向應(yīng)力是壓縮應(yīng)力)隨時(shí)間的變化,捕捉結(jié)構(gòu)上由“壓縮”應(yīng)力轉(zhuǎn)為“拉伸”應(yīng)力的位置處的溫度Tcritical,進(jìn)而判斷結(jié)構(gòu)長(zhǎng)期維持結(jié)構(gòu)完整性的可能性。
本文以結(jié)構(gòu)不連續(xù)區(qū)(也是壁厚最薄區(qū))為評(píng)價(jià)區(qū)域,選取其中3個(gè)典型評(píng)定截面(定義為路徑P1、P2和P3,如圖4所示)給出評(píng)價(jià)。
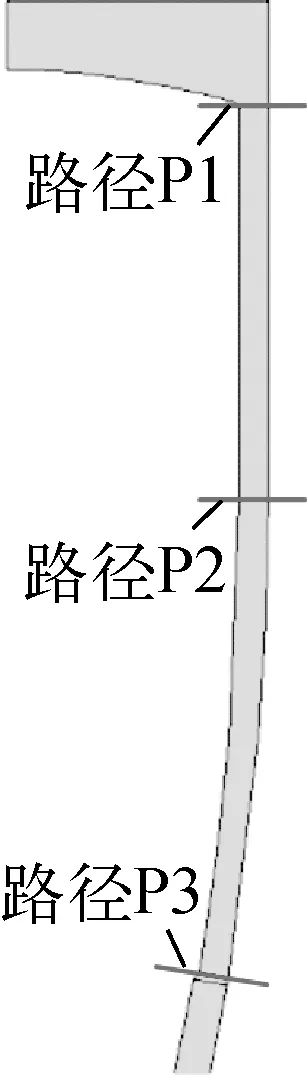
圖4 評(píng)定截面路徑Fig.4 Evaluation section path
圖5示出路徑P1損傷因子、環(huán)向應(yīng)力和子午線向/軸向應(yīng)力分布隨時(shí)間的變化,圖中橫坐標(biāo)x/t中的x為距內(nèi)壁的距離,t為路徑處的壁厚。
從圖5a可看出,只有在近內(nèi)壁面小范圍的壁厚區(qū)域內(nèi)的損傷因子超過(guò)1.0,其余大部分壁厚區(qū)域的損傷因子接近于0,說(shuō)明RPV結(jié)構(gòu)在高溫度梯度和0.1 MPa的內(nèi)壓作用下僅可能在近內(nèi)壁面小范圍的壁厚區(qū)域內(nèi)發(fā)生蠕變斷裂。
從圖5b、c可看出,路徑P1上環(huán)向應(yīng)力和子午線向/軸向應(yīng)力由“壓縮”轉(zhuǎn)為“拉伸”位置處的溫度Tcritical分別為400 ℃和320 ℃(對(duì)于P2和P3路徑的結(jié)果,限于篇幅,從略)。
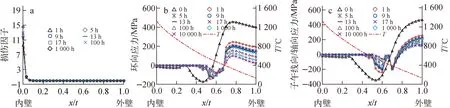
圖5 路徑P1損傷因子、環(huán)向應(yīng)力和子午線向/軸向應(yīng)力分布隨時(shí)間的變化Fig.5 Damage factor,hoop stress and meridian/axial stress on path 1 at different time
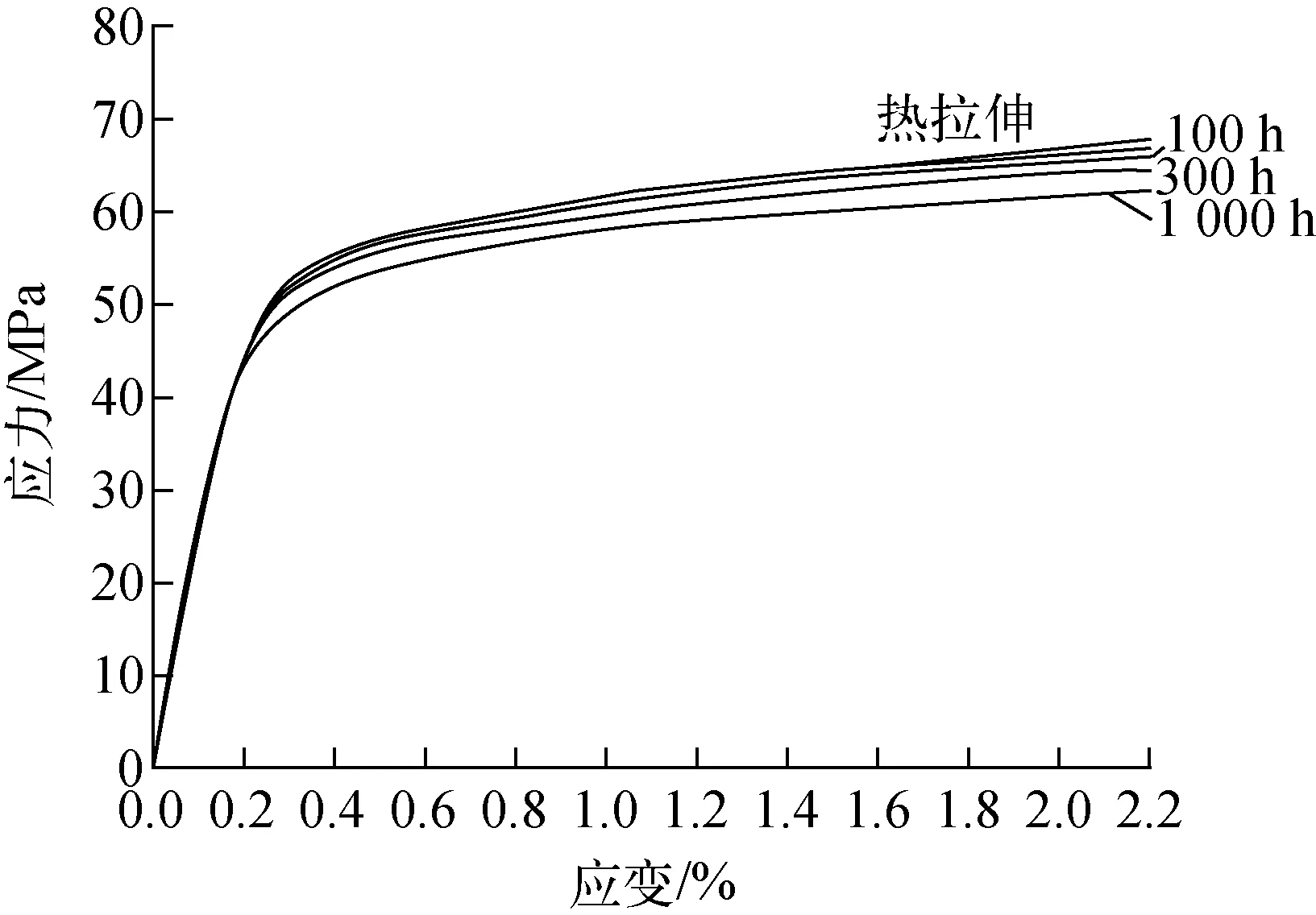
圖6 SA-508 Gr.3 Cl.1在399 ℃時(shí)的等時(shí)應(yīng)力應(yīng)變曲線Fig.6 Isochronous stress-strain curve of SA-508 Gr.3 Cl.1 at 399 ℃
ASME-BPVC-Ⅲ-NB-1120[13]中指出,當(dāng)溫度高于第Ⅱ卷D篇[14]中的溫度限制時(shí),材料的蠕變特性及持久特性將成為重要因素,SA-508 Gr.3 Cl.1在第Ⅱ卷D篇中的溫度限制Tcreep=371 ℃(700 ℉),因此,上述分析中P1路徑上環(huán)向應(yīng)力對(duì)應(yīng)的Tcritical=400 ℃,已高于Tcreep,即蠕變溫度區(qū)間在Tcreep至400 ℃的區(qū)域處于拉伸應(yīng)力狀態(tài),同時(shí)也注意到,該區(qū)域的應(yīng)力水平較低,且隨著時(shí)間的增加而下降,圖6示出了SA-508 Gr.3 Cl.1在399 ℃時(shí)的等時(shí)應(yīng)力應(yīng)變曲線[15],從曲線上看出,當(dāng)溫度處于399 ℃時(shí)且應(yīng)力小于約276 MPa時(shí),材料的蠕變效應(yīng)可忽略,因此,處于Tcreep至400 ℃區(qū)間的區(qū)域雖處于低水平的拉伸應(yīng)力狀態(tài),但不會(huì)發(fā)生蠕變斷裂。同時(shí),P2和P3路徑上環(huán)向應(yīng)力、子午線向/軸向應(yīng)力由“壓縮”轉(zhuǎn)為“拉伸”的位置處的溫度Tcritical均小于Tcreep。
此外,P1、P2和P3路徑內(nèi)壁面的區(qū)域雖可能發(fā)生蠕變斷裂,由于其外部相當(dāng)壁厚區(qū)域內(nèi)處于壓縮應(yīng)力狀態(tài),因此不會(huì)發(fā)生貫穿厚度截面上的失效(泄漏)。
4 結(jié)論
本文建立考慮內(nèi)壁面熔蝕的RPV有限元模型,在溫度場(chǎng)分析的基礎(chǔ)上,開(kāi)展蠕變計(jì)算,得到不同時(shí)刻下的應(yīng)力應(yīng)變響應(yīng),通過(guò)選取典型評(píng)定路徑并利用基于Larson-Miller參數(shù)的累積損傷理論進(jìn)行蠕變損傷計(jì)算及評(píng)價(jià),形成結(jié)論如下:結(jié)構(gòu)內(nèi)壁面區(qū)域雖可能發(fā)生蠕變斷裂,由于其外部相當(dāng)壁厚區(qū)域內(nèi)處于壓縮應(yīng)力狀態(tài),因此不會(huì)發(fā)生貫穿厚度截面上的失效;各危險(xiǎn)截面上三向應(yīng)力由“壓縮”轉(zhuǎn)為“拉伸”的位置處的溫度Tcritical多數(shù)低于蠕變溫度限制Tcreep,對(duì)于超過(guò)Tcreep的例外情況,由于Tcritical接近于Tcreep且應(yīng)力水平較低,蠕變效應(yīng)可忽略,因此,均不會(huì)發(fā)生蠕變斷裂。
可推斷,在考慮內(nèi)壓0.1 MPa的IVR條件下,RPV的長(zhǎng)期結(jié)構(gòu)完整性可保證。本文的分析結(jié)論為保證IVR條件下RPV的結(jié)構(gòu)完整性提供依據(jù),形成的研究方法可為后續(xù)核電廠RPV在IVR條件下的結(jié)構(gòu)完整性分析提供參考。

