單組率研究稀疏數據的Meta分析方法

劉 曼 陳文松 劉玉秀,3 陸夢潔 劉雅琦 袁陽丹

近年來，醫學研究中對單組率研究的Meta分析呈增長趨勢[1-3]，然而當遇到稀疏數據時，不顧方法應用條件盲目選擇的情況時有發生，導致合并結果的偏倚，甚至產生誤導的結論[4]。有學者指出，單組率研究的Meta分析若出現稀疏數據，尤其是零事件的研究較多時，常用的Meta分析方法統計性能不佳，應謹慎選擇[5]。本文針對單組率研究遇到稀疏數據時進行Meta分析的方法，擇優選出目前認為具有較好性能的基于Freeman-Tukey轉換、反正弦轉換的倒方差法和廣義線性混合模型(GLMM)方法，通過Monte-Carlo模擬比較其統計性能，為Meta分析的方法選擇提供依據、提出建議。

1 方法

Meta分析有3個重要方面，一是分析的框架，二是模型的選擇，三是異質性評價方法的選擇。

1.1 框架的選擇 單組率研究的常用Meta分析方法原理通常是基于正態分布的。對于發生率為p的總體，例數為n的樣本中某一事件的發生數e服從二項分布，若n足夠大且p不接近0或1，可用二項分布近似正態分布。然而，當n較小或p接近0或1時，由于分布的離散性，則不宜用二項分布近似正態分布。因此，二項數據建模最流行的框架是通過變換使之近似于正態分布，在進行Meta分析的倒方差法中，提出了幾種轉換方法，包括ln轉換(自然對數轉換)、logit轉換[6]、反正弦轉換[7]和Freeman-Tukey雙重反正弦轉換(FT轉換)[8-10]。前2種轉換在計算過程中，遇到零事件可能會面臨除零問題，盡管可以做連續性校正，但研究證明這些校正仍會產生偏倚，難以保證結果的穩定性，而后2種轉換則無需校正且可以保持較好的統計性能，因此不少文獻推薦選擇后兩者[6, 7,11]。

單組率的Meta分析還有另外1種分析框架即GLMM，是Stijnen等[10]提出的確切研究內似然模型(EWLM)，包括二項-正態模型(BN)和泊松-正態模型(PN)等[12]，可方便地實現稀疏二分類數據的Meta分析，他提出以各研究真實的分布代替其正態分布的假設，在單組率Meta分析中，最常用的是BN[13]，該模型包括2個部分，第1部分用二項分布對數據進行建模，假設事件數ei服從參數為pi，樣本量為ni的二項分布，即

第2部分是logit轉換后使用正態分布來模擬研究之間的異質性，即用正態分布對隨機效應進行建模

logit(pi)～Normal(μ,τ2)(2)

其中，μ是總體logit率的均值，τ2是logit尺度下的研究間方差(τ為標準差)。τ為0時則簡化為固定效應模型。令 logit(pi)=θi，因此事件數ei的真實分布為[5]，

ei～Binomial(ni, exp (θi)1+exp (θi))(3)

1.2 模型的選擇[14]在固定效應模型下，分析中的所有研究都具有共同的真實效應，合并效應是對共同效應大小的估計，其原假設是共同效應為0(對于差值)或1(對于比值)。在隨機效應模型下，假設研究中的真實效應是從真實效應的分布中抽樣的，原假設是這些效應的平均值為0(對于差值)或1(對于比值)。2種模型的選擇文獻已有詳細說明[15]，在此不贅述。固定效應模型下，若出現0事件，經模擬證明，FT轉換是優選方法，而在隨機效應模型下，因研究間變異差異較大，FT轉換可能難以保持穩定的統計性能，而在實際應用中，逆方差法應用較多，忽視了GLMM。

1.3 異質性評價方法的選擇[14]對于研究間方差τ2，目前常用的參數估計方法有3種。1種由Dersimonian和Laird提出的非迭代法[16]，另外2種是極大似然(ML)方法和限制極大似然(REML)方法。在倒方差法中，這些方法都可以應用，對于隨機效應模型，由于極大似然估計會導致方差的低估，故首選REML方法。對于二項式模型的GLMM，由于隨機效應的高維積分的密集計算，無法使用REML方法，因此大多數軟件都使用ML方法估計研究間方差。

2 Monte-Carlo模擬研究

考慮采用3個度量值評估FT轉換、反正弦轉換和GLMM在Meta分析應用中的統計性能[17]，包括點估計的相對偏倚、置信區間覆蓋率和平均寬度。所有模擬在SAS 9.4系統環境下實現。將每次Meta分析模擬的研究個數(k)設定為30，取常用的95%CI固定不變。考慮到樣本量和數據結構對結果的影響，設置了2個不同的總樣本量(6 000和60 000)，各樣本量下又分平衡和不平衡2種結構。總樣本量為6 000時，平衡結構的每個研究的樣本量設定為200，不平衡結構的最小樣本量為50，其他樣本以10為增量依次遞增至340。對總樣本量為60 000的情形，相應設置擴大10倍即可。模擬研究平均總體率(p)從非常罕見的事件(0.001、0.005、0.01)到相對常見的事件(0.05、0.10、0.30、0.50)變化，研究間標準差(τ)設置為0.005、0.3、1(logit尺度下)。基于以上模擬參數設置，共需模擬2×2×3×3×7=252種場景。基于Meta分析隨機效應模型框架，在不同模擬場景下，進行10 000次模擬，模擬分為2步，首先從給定的logit率[logit(p)]和研究間方差(τ2)的正態分布中模擬真實的logit率(ηi)，再從二項分布中模擬率為pi=eηi/(1+eηi)、樣本量為ni的Meta分析數據集。分別采用不同的變化參數設定進行Meta分析，獲得相應的點估計和95%CI估計。該隨機模擬過程反復多次進行，直至達到規定的模擬次數，再根據各次的模擬結果計算各性能評價指標。

3 結果

在不同的模擬場景下，通過Monte-Carlo模擬Meta分析獲得的不同方法的相對偏倚(圖1)、置信區間覆蓋率(圖2)和置信區間平均寬度(圖3)結果。總體來看，在總樣本量相同的情況下，平衡和不平衡2種樣本量結構下的各種方法的統計性能行為都非常接近；在總樣本量不同的情況下，不同方法間的行為表現存在明顯差別。

圖1顯示，總樣本量為6 000時，當研究間方差較小(τ<1)時，平均總體率>5%的各種方法的點估計均接近無偏；當研究間方差大時(τ=1)，FT轉換和反正弦轉換只有在率為50%時才接近無偏；而總體率<5%時，只有GLMM繼續保持無偏。總樣本量為60 000時，當研究間方差較小(τ<1)時，平均總體率>0.5%的各種方法的點估計均接近無偏；當研究間方差大時(τ=1)，FT轉換和反正弦轉換依舊表現較差，而GLMM無論在何種情況都接近無偏。

圖2顯示，樣本量為6 000時，當研究間方差較小(τ<1)時，平均總體率>5%的各種方法的置信區間的覆蓋率均接近名義水平；當研究間方差大時(τ=1)，FT轉換和反正弦轉換只有在總體率>30%時才接近名義水平，而GLMM整體上保持在名義水平附近。樣本量為60 000時，當研究間方差較小(τ<1)時，平均總體率>0.5%的各種方法的置信區間均接近名義水平；當研究間方差大時(τ=1)，FT轉換和反正弦轉換的覆蓋率轉換均較差，而GLMM的覆蓋率依舊保持在名義水平。圖3顯示，各方法間的置信區間的寬度無明顯差別，而隨著平均總體率和研究間方差的增大，各方法的區間寬度均明顯增大。

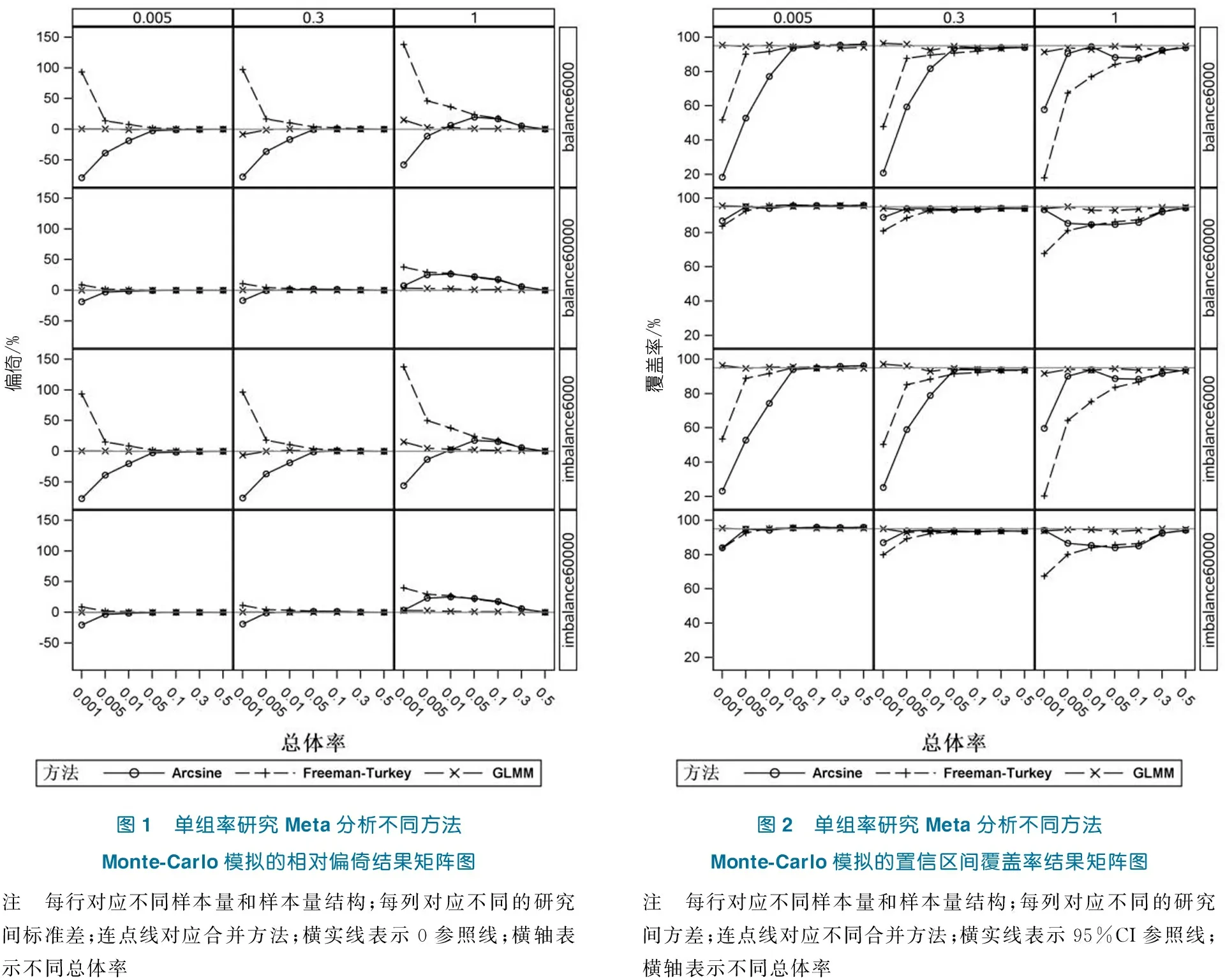
圖1 單組率研究Meta分析不同方法Monte-Carlo模擬的相對偏倚結果矩陣圖圖2 單組率研究Meta分析不同方法Monte-Carlo模擬的置信區間覆蓋率結果矩陣圖注 每行對應不同樣本量和樣本量結構;每列對應不同的研究間標準差;連點線對應合并方法;橫實線表示0參照線;橫軸表示不同總體率注 每行對應不同樣本量和樣本量結構;每列對應不同的研究間方差;連點線對應不同合并方法;橫實線表示95%CI參照線;橫軸表示不同總體率

圖3 單組率研究Meta分析不同方法Monte-Carlo模擬的置信區間平均寬度結果矩陣圖

4 GLMM的軟件實現

4.1 SAS實現 SAS中的GLMM是通過PROC NLMIXED實現的[18]，NLMIXED過程適合包括固定和隨機效應模型的非線性混合模型，考慮到隨機效應，可以為數據指定條件分布，包括正態、二項和泊松分布等，通過NLMIXED過程擬合的模型可以看作是通過MIXED過程擬合的隨機模型的擴展，在MIXED過程中可以通過ML和REML估計參數，而NLMIXED過程僅能實現ML。另外由于標準Wald方法沒有考慮τ估計的不確定性，NLMIXED過程的統計基礎是基于t分布的，其自由度df=N-l[19]。

用NLMIXED過程做Meta分析可分別估計固定效應和隨機效應模型。固定效應模型中，需指定總體率的初始值及取值范圍，并指定事件數的分布類型。在隨機效應模型中，除了總體率的初始值，還需指定研究間方差的初始值，并指定隨機項。Meta分析的GLMM的NLMIXED詳細過程見本文附錄。

4.2 R語言實現 R語言的“meta”包中的“metaprop”函數可用來做單組率的Meta分析，通過指定“metaprop”函數中的參數“method=“GLMM”，R語言就會自動調用“rma.glmm”函數擬合GLMM。默認情況下，模型中各個系數的檢驗統計量以及相應的置信區間是基于標準正態分布的，作為一種替代方法，可以設置“rma.glmm”函數中的參數“test ='t'”，該方法基于t分布獲得各個系數和置信區間。對于異質性檢驗，該函數會自動執行2種設定。①Wald型檢驗，用于檢驗與飽和模型中添加的啞變量相對應的系數的顯著性。②似然比檢驗，檢驗相同的系數集，但是通過計算-2倍固定效應和飽和模型的對數似然差來進行。對于由rma.glmm函數擬合的模型類型，這2個檢驗并不相同，甚至可能導致相反的結論。

GLMM模型不需要計算單個研究的觀察結果，因此，當事件數為零時，不必在事件計數中添加常數，直接令p=0不是問題(所有研究均為零事件的極端情況除外)。原則上，單個研究的權重可以從每個單獨研究的似然貢獻中得出，然而，該信息目前在R軟件中不可用，所以在R中無法獲得各研究權重，且只適用于logit轉換，對于單組率的其他轉換則只能使用倒方差法。

4.3 STATA實現 STATA中的“metan”命令可用來做Meta分析[20]，在“metan”中，使用基于漸近方差的正態分布來計算置信區間。對于率，此區間可能包含不允許的值，尤其是當率接近0或1時。當率為0或1時，由于估計的標準誤為零，因此無法計算置信區間，“metan”命令會自動從合并計算中排除率等于0或1的研究。

Nyaga等[21]在此基礎上開發出了“metaprop”命令，以補充“metan”，允許使用Wilson得分法和Clooper-Pearson確切法計算95%CI并結合了FT轉換，該命令還可以使用二項分布對研究內變異進行建模。需要STATA 10或更高的版本，通過鍵入“ssc install metaprop”命令安裝，還可以下載“metaprop”的更新“metaprop_one”，該命令可用來擬合GLMM，更新后的命令需要STATA 13版本。具體語句見附錄。

5 案例分析

一項發熱嬰兒單核細胞增多性李斯特菌和腸球菌檢出率的Meta分析[4]就遇到了稀疏數據的問題。該研究為了評估由單核細胞增多性李斯特菌和腸球菌引起嚴重細菌感染的患病率，納入了15項研究，共計20 703份血樣，分別對李斯特菌和腸球菌引起菌血癥的患病率做Meta分析，兩者的患病率均不高，因此該Meta分析中出現了大量的零事件，尤其是李斯特菌，除了2項研究各出現1例事件外，其余研究的患病率均為0，用R語言中“meta”包中的“metaprop”函數對李斯特菌菌血癥發生率做Meta分析的森林圖見圖4，其中方法選擇GLMM，各研究95%CI方法選擇Clopper-Pearson法。用GLMM擬合的結果為0.01%(95%CI：0～0.04%)，FT轉換的結果為0.02%(95%CI：0～0.07%)，反正弦轉換的結果為0(95%CI：0～0.01%)。

原文中首先對本組資料的零事件進行校正，得到的結果為0.03%(95%CI：0～0.06%)，該結果與GLMM的結果有明顯差別。

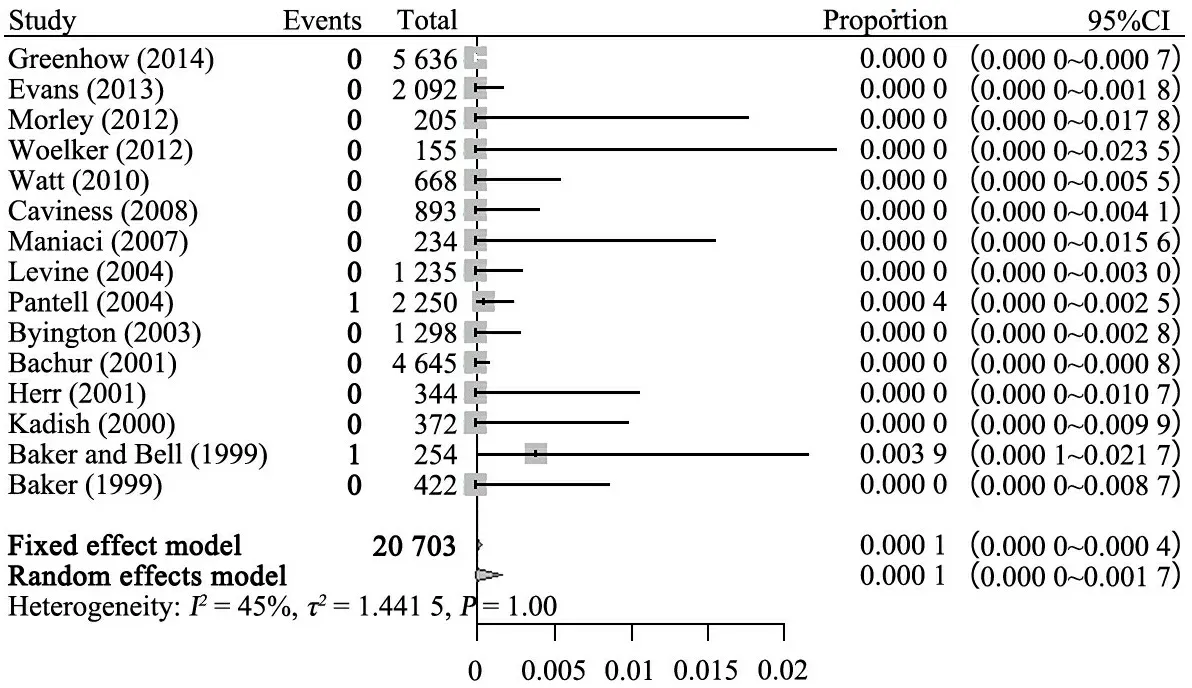
圖4 單核細胞增多性李斯特菌引起嚴重細菌感染的患病率森林圖

6 討論

本文討論了單組率研究出現稀疏數據時常用的Meta分析方法，包括基于FT轉換和反正弦轉換的倒方差法和GLMM方法，通過Monte-Carlo模擬，設置多種模擬分析場景，比較了3種方法的統計性能，結果發現GLMM方法具有較好的統計性能且對稀疏數據具有穩健性，應作為單組率研究稀疏數據Meta分析的首選方法。同時介紹了隨機效應模型下GLMM方法的原理及其在不同軟件中的實現，為醫學研究者提供了實用參考。

盡管FT轉換可以保留所有研究而無需對零事件做校正，且在固定效應模型下，大多數情況下的FT轉換都可以保持優良的統計性能，這在之前的模擬中也得到了驗證[11]，但當研究數增大且研究中零事件增多時，FT轉換的統計性能不佳；在隨機效應模型下，隨著研究間方差的增大，FT轉換的性能難以滿足統計學要求，因此應謹慎使用。無疑，GLMM不需要對零事件進行校正，其優異的統計性能成為單組率研究Meta分析隨機效應模型下的首選。但該方法也并非完美無缺，對于較小的樣本量、極低的事件發生率和較大的研究間方差，各研究會出現較多的零事件，此時GLMM的點估計會出現偏倚，好在這一問題在極低事件率時并不重要。

事實上，GLMM在很多軟件系統中都有設置，例如通過SAS中的PROC NLMIXED過程、R語言的“rma.glmm“函數和STATA的metaprop_one命令等，均不難實現。因此，當面臨單組率研究稀疏數據的Meta分析時，不應再受限于軟件實現的困難，應首選GLMM方法。

附錄

1.采用SAS實現固定效應模型Meta分析的方法

proc nlmixed data=Meta_data df=1e6;

parms p=0.5;

bounds 0

model e～binomial(n,p);

estimate "logit(p)" log(p/(1-p));

run;

2.采用SAS實現隨機效應模型Meta分析的方法

proc nlmixed data=Meta_data DF=1E6 qpoints=100;

parms theta=-4.5 to -0.5 by 0.5 sigmasq=0.3;

pi=exp(logodds)/(1+exp(logodds));

model e ～ binomial(n,pi);

random logodds ～ normal(theta,sigmasq) subject=study;

run;

3.采用R軟件實現Meta分析的方法

library("meta")

4.采用STATA軟件實現Meta分析的方法

ssc install metaprop_one

metaprop_one e n, random logit