證明絕對值不等式的八個推理策略

江蘇省金湖縣第二中學 (211600) 梁加林

含絕對值的不等式是一個綜合性問題，而其與不等式相結合的問題是高考和其他選拔性考試中加大區分度的重要選擇內容之一，其求解過程需要綜合考慮，在用好絕對值不等式的性質的同時，需要考察具體題目的特點，研究出題者的考試意圖和目的，制定合理可行的富有特色的將它方案．本文從如何分析題目、解決具體問題的角度出發，介紹八種常見的推理策略，希望給讀者朋友一點啟發．

一、分析推理

在一些相對復雜的不等式問題的推理過程中，經常采用“由果索因”的手段，即從結論出發步步逆推，直到找到能使結論成立的理論依據，這樣也就完成了題目證明的過程．

例1 已知函數f(x)=|x+1|，若|a|>1,|b|>1，求證：f(ab)>f(a)-f(-b).

證明：因為f(a)-f(-b)=|a+1|-|-b+1|≤|a+1-(-b+1)|=|a+b|，所以要證f(ab)>f(a)-f(-b)，只需證|ab+1|>|a+b|，即證|ab+1|2>|a+b|2，即證a2b2+2ab+1>a2+2ab+b2，即證a2b2-a2-b2+1>0，即證(a2-1)(b2-1)>0.因為|a|>1，|b|>1，所以a2>1，b2>1，所以(a2-1)(b2-1)>0成立，所以原不等式成立.

評注：由于要證的不等式中含有絕對值符合，比較復雜，直接用綜合推理不太順暢，所以采用了分析法.一般的，如果含有分式、根式、絕對值等問題采用分析法效果是明顯的．

二、活用公式

利用絕對值不等式|a|-|b|≤|a±b|≤|a|+|b|,進行“放大”或“縮小”是解決與絕對值相關的不等問題最常用的思路．

例2 已知f(x)=ax2+bx+c對于一切實數x∈[-1，1]都有|f(x)|≤1，證明對于一切x∈[-1，1]都有|2ax+b|≤4．

解析：從|f(x)|≤1到|2ax+b|≤4需通過一些特殊的函數值來建立不等關系，如f(0),f(-1),f(1)等，然后用絕對值不等式來證明．依題意可知|f(0)|≤1，|f(-1)|≤1，|f(1)|≤1，即|c|≤1，|a+b+c|≤1，|a-b+c|≤1,則|2a+2c|≤|a+b+c|+|a-b+c|≤2,即|a+c|≤1,所以|2a+b|=|(a+b+c)+(a+c)-2c|≤|a+b+c|+|a+c|+|2c|≤4, 且|2a-b|=|(a-b+c)+(a+c)-2c|≤|a-b+c|+|a+c|+|2c|≤4,又當x∈[-1,1]時, |2ax+b|≤{|2a+b|,|2a-b|}，所以|2ax+b|≤4．

評注：在“放大”或“縮小”的過程中，其關鍵是合理的配湊，就是將需要證明的結論通過適當的配湊分解成與已知條件相關的不等式．本題中利用兩次“放大”后達到了解題目的，要注意在“放大”或“縮小”時必須保持不等號方向一致．

三、及時消參

如若所給的條件式中只含有一個參數，并且也已知這個參數的范圍，可直接運用絕對值不等式的性質進行放縮，消去參數，達到解題目的．

評注：在解題中抓住了|a|≤1這個關鍵條件，通過分離參數再運用絕對值不等式的性質進行放縮處理，消去了參數a，這是為后續的解題掃清了障礙．

四、巧取特值

在已知的函數式中，若含有字母系數，其中取特殊值是一個重要的解題手段，由此可顯露出所求不等式中有關部分的內在聯系，從而確定可行的解題方案．

例4 已知a,b,c∈R, 若已知函數f(x)=ax2+bx+c,g(x)=ax+b, 當x∈[-1,1]時，有|f(x)|≤1成立．(1)證明：|c|≤1；(2)當x∈[-1,1]時，求證：|g(x)|≤2．

證明：(1)由于x∈[-1,1]時，|f(x)|≤1, 而0∈[-1,1]，則必有|f(0)|=|c|≤1．

(2)由于g(x)=ax+b為單調函數, 其圖像是一條直線，要證|g(x)|≤2, 只須證|g(±1)|≤2,由|xg(x)|=|ax2+bx|=|f(x)-c|≤|f(x)|+|c|≤1+1=2, 取x=±1時, 有|g(±1)|≤2，故必有|g(x)|≤2成立．

評注：本題中參數多，含有兩個函數式，要完成題目的證明首先充分挖掘了一次函數的有關性質，利用特殊值將待證式進行簡化；然后再挖掘兩個函數之間的特殊關系，并巧妙地合理配湊，使整個證題過程變得順暢自如．

五、重新組合

在給定的定義域內，通過取特殊值，建立含參數的等式，然后以消去參數為目的進行有目標的重新組合，再運用絕對值不等式的性質進行放縮處理，達到解題的目的．

評注：本題中的結論與一個常數有關，那么如何消去題目中的參數就是解題目標，利用給出的條件先表示出含參數等式，通過有目的地配湊，再由不等式性質進行整體處理，達到證題目的，這些都是證明含絕對值的不等式常用手段，應該得到理解和重視．

六、引入參數

如果在用拼湊組合消去系數時，遇到了困難，可通過引入新參數，然后再運用待定系數法求出這個參數，建立有關的等式．

例6 設函數f(x)=ax2+bx+c對于一切x∈[-1,1]都有|f(x)|≤1，求證：對于一切x∈[-1,1]都有|3ax+b|≤6．

證明：設g(x)=3ax+b，g(1)=mf(1)+nf(-1)+kf(0)，則3a+b=m(a+b+c)+n(a-b+c)+kc=(m+n)a+(m-n)b+(m+n+k)c，通過比較多項式的系數可知：m+n=3且m-n=1且m+n+k=0；解由此三式聯立所得方程組得：m=2；n=1；k=-3；即g(1)=2f(1)+f(-1)-3f(0)．又對于一切x∈[-1,1]都有|f(x)|≤1，則|f(1)|≤1；|f(-1)|≤1；|f(0)|≤1；故而|g(1)|=|2f(1)+f(-1)-3f(0)|≤2|f(1)|+|f(-1)|+3|f(0)|≤2+1+3=6．同理可證|g(-1)|≤6，由一次函數的性質可知|g(x)|≤6，即|3ax+b|≤6．

評注：待定系數法是解決多項式“恒等”問題的有力工具，在本證題中比較恰當地使用了此法，給人有打破常規、耳目一新的感覺，降低了解題的難度．

七、反解系數

如若題目中欲證明與系數相關的不等式，可通過取特殊值將所求系數用關于特殊的函數值表示出來，然后再運用不等式進行放縮推理．

例7 若f(x)=ax2+bx+c(a,b∈R)在區間[0,1]上恒有|f(x)|≤1，求證：|a|+|b|+|c|可能的最大值為17．

八、抓住性質

對于二次函數問題，二次函數的圖像和性質是解決問題的有力武器，及時地加以運用，可簡化解題過程，提高解題效率.

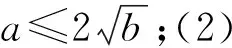
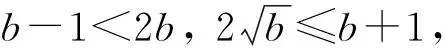
評注：在解決本題第(1) (2)問時，及時的運用了二次函數的圖象及性質，再結合已知的絕對值不等式的條件，運用絕對值的意義進行轉化，這樣就建立了相關的不等式組，這就是抓住了解題的關鍵所在，將難點輕松化解了．