同時取送貨的 “ 最后一公里 ” 車輛路徑問題研究

袁雨果

（集美大學誠毅學院商船系，福建廈門361021）

一、引言

改革開放以來，我國經濟社會的快速發展、經貿活動的不斷增多，特別是電子商務的發展，為快遞行業快速發展提供了良好的契機。國家統計局數據表明，2010—2019 年這10 年我國快遞業務迅速發展，業務量增長26 倍，業務收入也相應地由574.6 億元提升至7 498 億元①，如圖1 所示。一方面快遞行業在增量市場（如農村快遞業務） 仍舊大有可為，另一方面快遞企業在存量市場上競爭卻不斷加劇。為了應對激烈的市場競爭環境，各快遞企業都試圖通過優化自身物流系統，以達到提升效率、降低成本和增強服務滿意度的目標。近年來，客戶退貨維修或者物品回收等需求不斷增加，一些快遞企業也傾向于在進行 “ 最后一公里 ” 配送的同時攬收客戶需要寄出的物件（如京東物流） 以提升物流服務效率，使得在 “ 最后一公里 ” 配送過程中整合正向物流和逆向物流成為企業提升運營效率和降低物流成本的重要途徑[1]。

電子商務物流配送可以大致分為三個階段，即倉儲、主干網運輸和 “ 最后一公里 ” 配送[2]，其中 “ 最后一公里 ” 配送是指將物品從倉儲中心發送給終端客戶的過程[3]。很多研究指出， “ 最后一公里 ” 配送極大地影響電商物流的服務質量和成本[2，4]，也是非常復雜的環節，因為它直接與終端客戶接觸，訂單數量大而規模小，而且終端客戶對配送方式、配送時間等要求都具有高度個性化和變動性等特點。

在此背景下，研究 “ 最后一公里 ” 車輛路徑優化問題時考慮正向和逆向物流整合具有重要的意義。相比一般的 “ 最后一公里 ” 配送，本問題更為復雜，它包括兩個交互影響的階段：車輛配送和攬貨任務的分配、車輛路徑的優化。這個問題可以被抽象為一個同時取送貨的帶有時間窗的車輛路徑規劃問題（Vehicle routing problem with simultaneous pick-up and delivery with time windows（VRPSPDTW））。VRPSPD已經被廣泛證明是一個NP 難問題，很難通過精確算法高效而準確地解決大規模VRPSPD[5]，而啟發式方法則被認為是解決這類NP 難問題的有效方式。為此，結合遺傳算法和變鄰域搜索算法，設計了一個包括3 個步驟的啟發式方法。通過構建100 個仿真場景，并通過統計分析的結果驗證了該啟發式方法具有較好的性能。

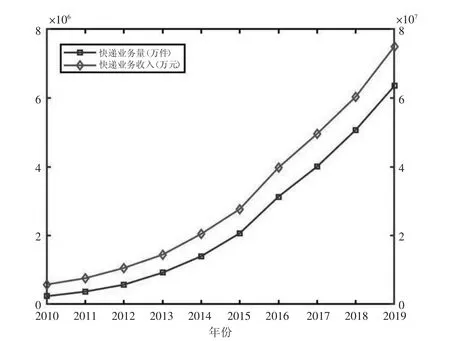
圖1 2010—2019 年我國快遞行業發展情況

二、文獻綜述

（一） “ 最后一公里 ” 物流問題

近年來我國電子商務快速發展，同時帶動了快遞等相關產業的發展。國家統計局數據表明，過去10 年快遞業務量和業務收入年均增長率分別達到44%和33%①。然而，在電商物流快速發展的過程中也暴露出了一些問題，特別是 “ 最后一公里 ” 配送成為制約電商物流提升服務質量和降低物流成本的關鍵環節[6，7]。為了解決 “ 最后一公里 ” 配送存在的問題，一些創新的配送方式不斷被設計出來，比如自助收發箱和顧客自提站等模式[8]：Mikko 等[9]和Song 等[10]的研究均表明，相比傳統配送方式，在 “ 最后一公里 ” 配送環節中采用自助收發箱模式可以有效降低物流成本、提升配送效率。

盡管上述多元化的配送方式在一定程度上提升了電商物流 “ 最后一公里 ” 配送的效率，但是無法解決車輛回程空載所造成的成本問題。為了進一步降低 “ 最后一公里 ” 配送的成本，學界和業界都開始探索在 “ 最后一公里 ” 中整合正向物流和逆向物流，即考慮在進行配送的同時實現攬貨。比如，郭月[11]分析了農村地區 “ 最后一公里 ” 配送和 “ 最初一公里 ” 攬收存在的主要問題，如需求量不足、配送成本高、設施不完善等，為此提出了 “ 選擇取送貨 ” 模式，從而為物流企業網點下沉提供有效的解決方案；何瑩瑩[12]針對家電行業中存在頻繁的退換貨從而導致逆向物流的現象，構建了考慮同時取送貨的家電物流路徑優化模型，并設計了混合粒子群算法進行求解。由此可見，同時考慮配送和攬收是傳統 “ 最后一公里 ” 配送的變體，可以通過同時取送貨的車輛路徑問題進行建模。

（二） 同時取送貨的車輛路徑優化

車輛路徑問題（Vehicle routing problem，VRP）最早由Dantzing 和Ramser[13]于1959 年提出，它是運籌學的一個熱門研究問題。由于其應用的廣泛性和在經濟社會發展（如物流、交通等） 中的重要價值，國內外很多學者針對VRP 進行了大量的研究，并提出多種變體以更好地解決所研究的問題。這其中，Min[14]針對圖書館取送書任務的實際，在VRP 的基礎上考慮同時取送貨的問題，首次提出了VRPSPD。在此之后，很多學者開始嘗試基于VRPSPD 解決物流和交通等領域的問題，比如：Liu[15]將VRPSPD 運用于家庭醫療物流優化中，并針對該問題構建了兩個混合整數規劃模型，同時提出了相應的解決算法；Shi[16]同樣針對家庭醫療物流問題，提出了一種隨機規劃模型；Alshamrani[17]則將VRPSPD 運用于解決具有逆向物流的美國紅十字會的血液配送問題，并提出了解決該問題的啟發式算法。現有研究往往根據所解決問題的特征，對VRPSPD 做進一步拓展，形成一些新的變體，如：考慮車輛異質性（Heterogeneous VRPSPD）[18]、考慮車輛存在多個起止點的情況（Multi-depot-VRPSDP）[19]、考慮多層次配送問題（Multi-echelon VRPSPD）[20]、研究車輛行駛時間隨機的情況（Stochastic travel-time VRPSPD）[21]和節點具有時間窗約束的情況（VRPSPD-time windows）[22]。同時，這些研究提出了大量的算法來求解VRPSPD相關的問題，如蟻群算法[23]、粒子群算法[24]、局部搜索算法[25]、遺傳算法[26]、分支定界算法[27]、變鄰域搜索算法（VNS）[28]、分支定界和離散螢火蟲算法（DFA） 等[29]，以及將上述若干種算法相結合設計的啟發式方法。

三、數學模型構建

整合正逆向物流的 “ 最后一公里 ” 車輛路徑優化問題可以視為考慮同時取送貨的帶有時間窗的車輛路徑問題（VRPSPDTW）。在保證該問題的主要特征的前提下，為突出主要問題特征而不失一般性，做出如下假定：1.所有車輛的起止節點都為同一個物流配送站點；2.一個客戶可能只需要配送服務或只需要攬貨服務，或兩種服務同時需要；3.同一個客戶有且僅有一臺車輛服務；4.每臺車輛都完全相同。為了便于問題的描述，表1 羅列了所涉及的變量及其相應的解釋。

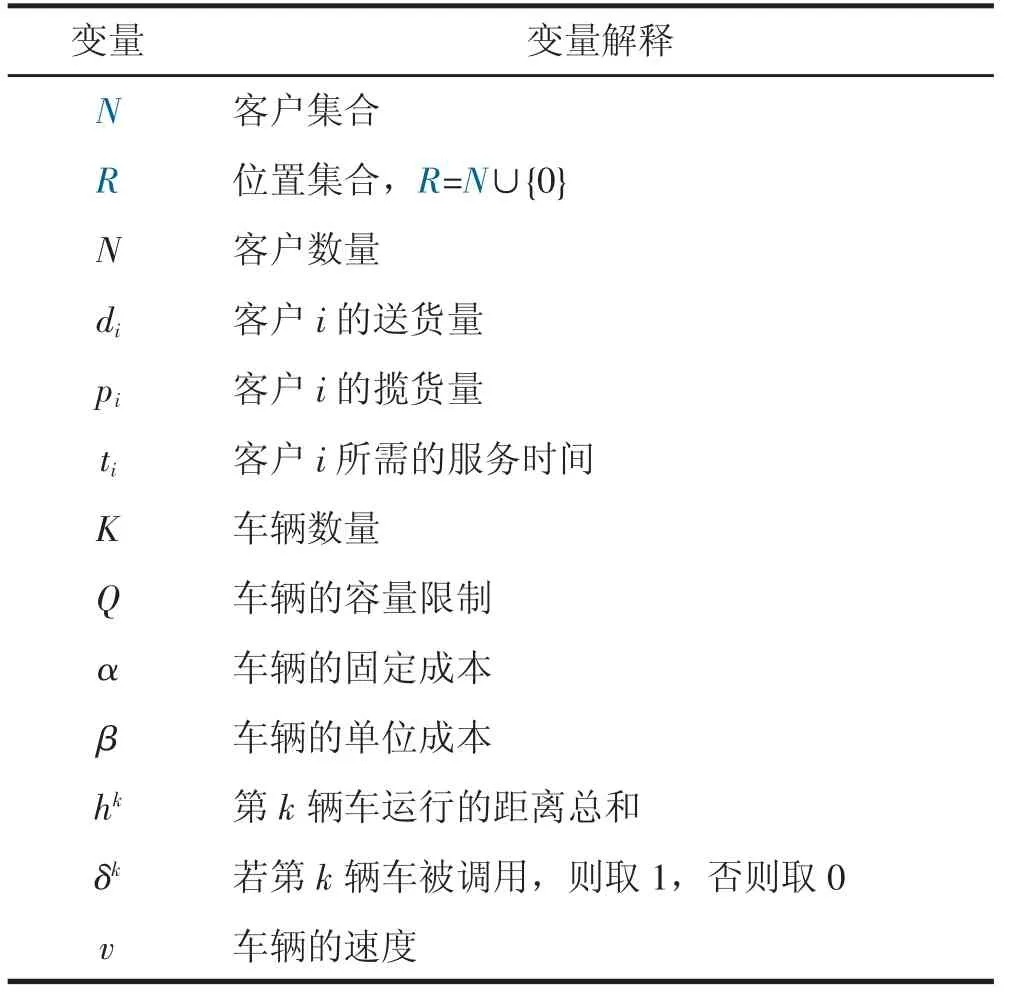
表1 變量定義及解釋

（一） 目標函數

如果車輛k 從客戶i 直接到客戶j，則0-1 離散變量為1，否則則車輛k 行駛的總距離hk可以通過式（1） 計算，其中cij為客戶i 與客戶j 之間的空間距離。如果車輛k 被調用，則0-1 變量δk=1，否則δk=0，如式（2） 所示。本研究的目的是實現所有配送和攬收任務的總成本最低，如式（3） 所示，式中α 表示使用一臺車輛的固定成本，而β 則表示每輛車單位距離所需要的變動成本。

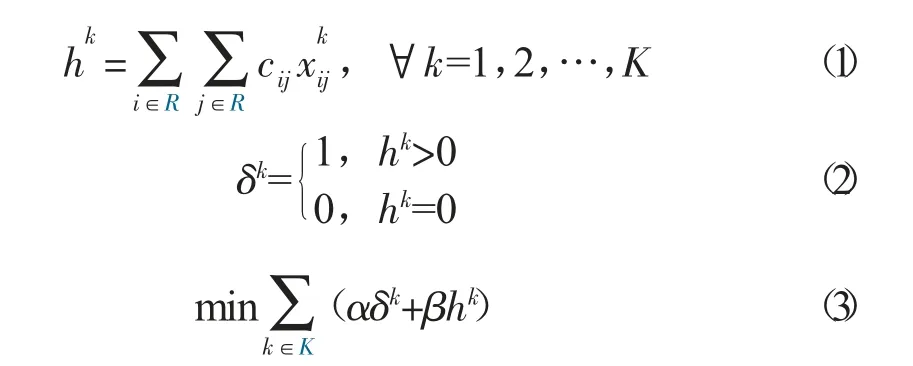
（二） 約束條件

所有客戶的配送或攬貨需求都要被滿足，且每個客戶有且只有一臺車輛服務，如式（4） 所示，其中N 表示客戶位置集合，R 為所有位置集合（R=N∪{0}）。根據上述假設，所有車輛的起止點都為相同的物流站點，如式（5） 所示。式（6） 確保車輛空間路徑的連通性，即車輛服務客戶后需要離開該客戶。所使用車輛的數量不能超過現有最大車輛數量K，如式（7） 所示。

青春如果沒有了奮斗，沒有了掙扎，沒有了希望，沒有了絕望，還叫什么青春？青春是一生當中最迷茫、焦慮、充斥著絕望、挑戰的時候，但是為什么所有的人都說青春美好呢？

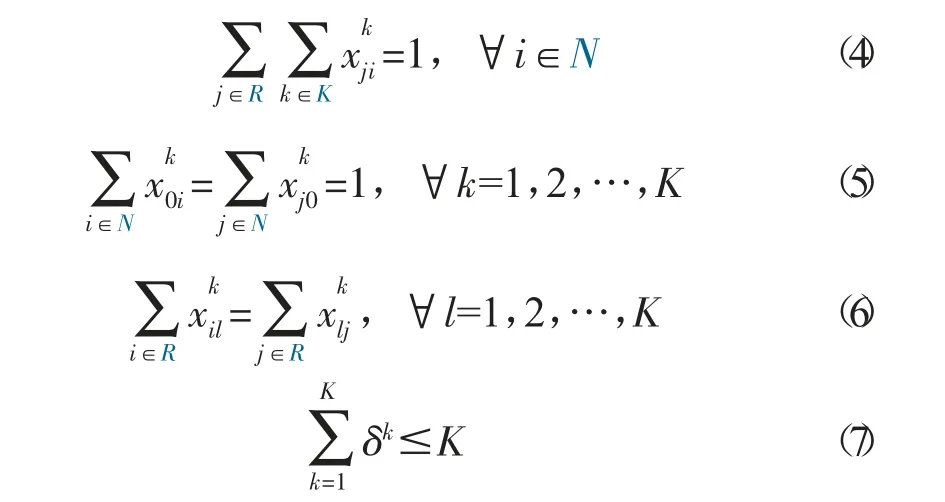
yij為經過弧（i，j）的客戶i 之前的客戶攬貨總和，而zij為經過弧（i，j）的客戶i 之后的客戶貨物配送總和。客戶攬貨和送貨的情況分別如式（8） 和（9）所示，每輛車的載貨量在任意時刻都不能超過車輛最大容量Q，如式（10） 所示。

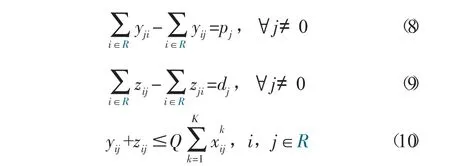
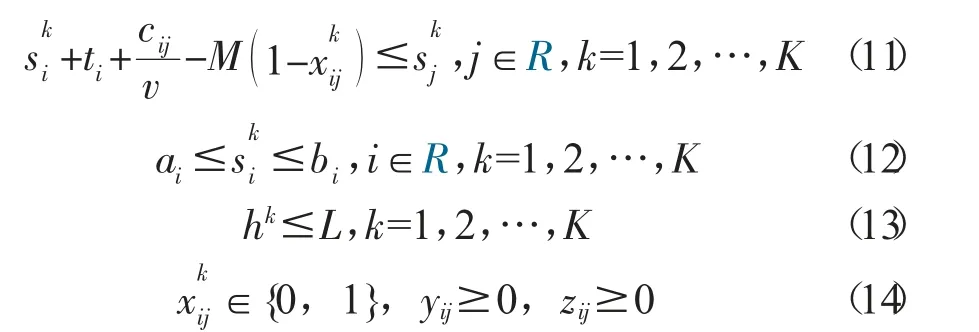
四、算法設計

VRPSPD 已經被廣泛證明是一個NP 難問題，很難通過精確算法高效而準確地解決大規模VRPSPD[5]。為此，結合遺傳算法和變鄰域搜索算法，設計一個包括3 個步驟的啟發式方法，該方法的流程圖如圖2 所示。

（一） 解編碼

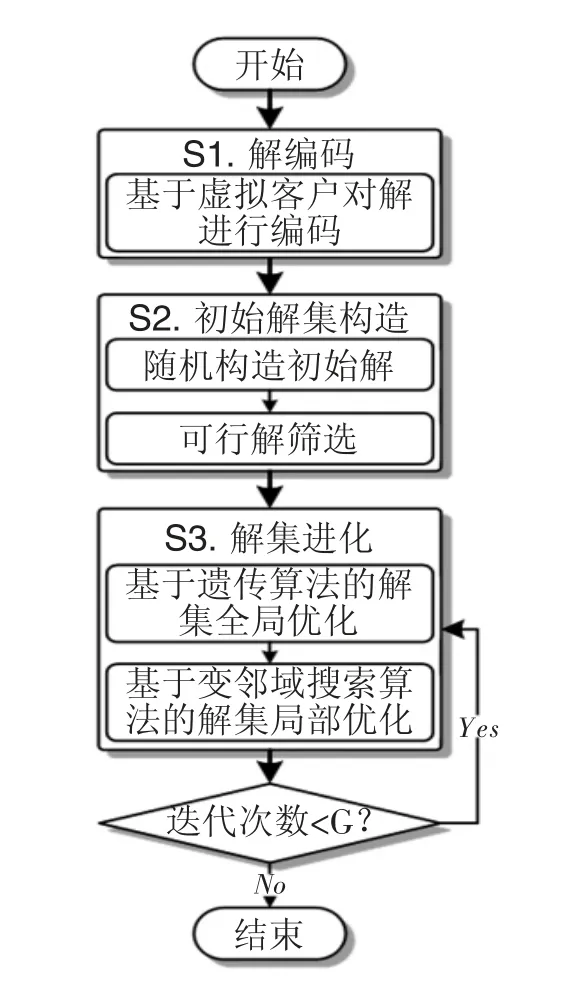
圖2 算法流程圖

根據表1 的定義，車輛數量為K、客戶數量為N。在解編碼過程中引入虛擬客戶的概念來構建染色體，每條染色體代表一個解，具體處理如下：隨機確定一個0～K-1 的整數作為虛擬客戶的數量，則該問題可以轉換為單車輛的路徑優化問題，即車輛從物流中心出發，完成所有任務后，又回到同一物流中心。以圖3 為例來說明解編碼的過程，在該圖中包括12 個客戶，4 輛車。在0 到3 之間隨機產生一個整數。假設隨機產生的數為2，標記為13 和14。對客戶集{1，2，…，13，14}排序，假定得到的一條染色體為0-3-4-7-9-13-10-1-2-5-14-8-6-11-12-0。將染色體中的虛擬客戶（13 和14） 替換為物流配送中心0，即可得到0-3-4-7-9-0-10-1-2-5-0-8-6-11-12-0。以 “ 0 ” 為標記將該染色體進行拆分，得到{0-3-4-7-9-0}，{0-10-1-2-5-0}和{0-8-6-11-12-0}等3 條子染色體，分別表示3 輛車所分配的客戶及線路。

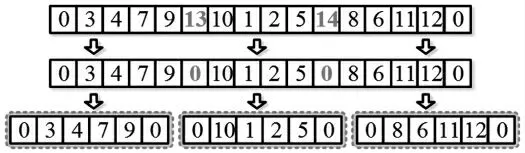
圖3 解編碼過程（示例）

（二） 初始解集構造

根據上述解編碼方式，可以構造大量解。然而，在構建過程中也可能會產生一些違反前述約束條件的解，可稱為非可行解。為了提升后續解優化的效率，需要提前將非可行解刪除，只允許可行解進入初始解集。初始解產生流程如下：

（1） 引入n 個虛擬客戶（0≤n≤K-1），構建客戶集合{v1，…，vN，vN+1，…，vN+n-1}；

（2） 基于（1） 得到的客戶集，根據前一節假定生成一條染色體以表征一個解；

（3） 拆分（2） 中生成的染色體，以得到每輛車的服務客戶及物流線路；

（4） 計算車輛完成所有任務所行駛的距離hk、整個過程中車載重量、服務每個客戶的時間（5） 若該解為可行解，即滿足各個約束條件，則將該染色體保存至初始解集合中，否則舍棄該染色體并重新返回步驟（1）；

（6） 如果初始解集合中包含的解數量達到算法預設的種群規模數量，則初始解集合構造的過程結束，否則返回步驟（1） 以生成新的解。

（三） 解集進化

解集進化是整個啟發式方法的核心環節，為了提升方法的性能，根據本問題的特征，將進化過程分為兩個階段：全局優化和局部優化。遺傳算法最早由Holland 在1975 年提出，由于具有較強的全局搜索能力等眾多特點，遺傳算法被廣泛應用于解決車輛路徑優化問題[26]。由Mladenovic＇和Hansen 提出的變鄰域搜索算法通過系統地執行鄰域變換程序以獲得更好的解，它具有很好的局部搜索能力[30]。根據上述兩種方法的特點以及本問題的特征，本啟發式方法在全局優化中采用遺傳算法，而局部優化則采用變鄰域搜索算法。

1.全局優化

遺傳算法包括交叉互換、變異和復制等算子，本啟發式方法在進行全局優化時采用單點變異和雙點變異兩種算子。分別以圖4 和圖5 來說明單點變異和雙點變異的過程。對于單點變異，首先從解集中隨機選擇一個解（如3-4-7-9-13-10-1-2-5-14-8-6-11-12），并從該染色體中隨機選擇一個基因（如圖4 的 “ 1 ” ）。以該變異點為節點，將染色體截取為3-4-7-9-13-10 和2-5-14-8-6-11-12 兩個染色體片段，并交換兩個染色體片段的位置以形成新的染色體，即：2-5-14-8-6-11-12-1-3-4-7-9-13-10。

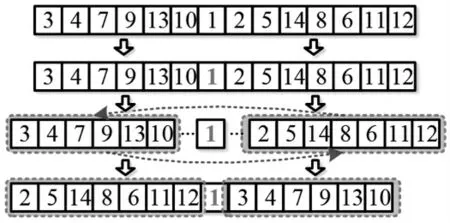
圖4 單點交叉變異

染色體雙點變異的過程如圖5 所示，同樣從解集中隨機選擇一條染色體（如2-5-14-8-6-11-12-1-3-4-7-9-13-10），并在該染色體中任意選擇兩個基因（如圖5 的 “ 8 ” 和 “ 4 ” ）。以兩個變異基因為節點將染色體截取為3 個片段：2-5-14，6-11-12-1-3 和7-9-13-10。其中，采用倒序的方式對兩個變異基因間的片段進行重新排序，從而得到新染色體，即2-5-14-8-3-1-12-11-6-4-7-9-13-10。

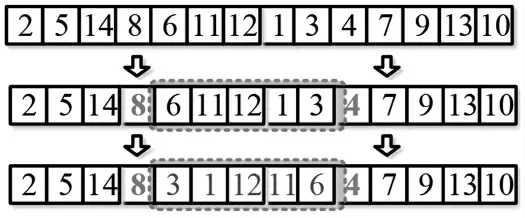
圖5 兩點交叉變異

2.局部優化

由于VNS 具有結構簡單和魯棒性較強等特點[31]，因此被廣泛應用于VRP 的相關研究中[28]。VNS 系統地將鄰域分為兩個相互作用的階段，變鄰域下降階段（VND） 的目的在于得到局部最優，而擾動階段來跳出當前局部最優。這里，采用兩種擾動策略來完成VNS 的擾動：1） 隨機移動虛擬客戶在染色體的位置，如圖6（a） 所示。2） 調整虛擬客戶的數量，如圖6（b） 所示。具體而言，1） 當現有染色體的虛擬客戶數量為K-1，則隨機減少一個虛擬客戶；2） 當現有染色體的虛擬客戶數為0 時，則增加一個虛擬客戶并隨機插入到染色體的其中一個位置；3） 當現有虛擬客戶的數量介于1 和K-2 之間，則隨機增加或減少一個虛擬客戶。VND 中依次包含的結 構 有Insert、Move-Best、Two-Opt、Swap-Best、Extract-Insert 和Extract2-insert[32]。

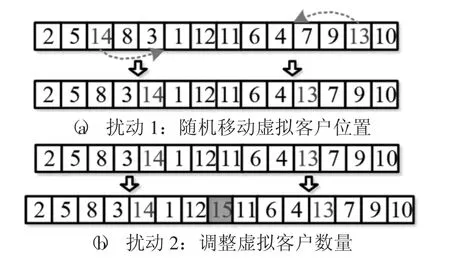
圖6 兩個VNS 擾動策略實例

在局部優化中基于上述2 個擾動策略和6 個鄰域結構：首先產生一個初始解，并執行第1 個擾動策略以得到該初始解的擾動解，記為S（i）；針對該擾動解S（i），依次執行上述6 個鄰域結構，不斷優化該擾動解，直至找到局部最優解。如果找到的局部最優解優于S（i），則重復執行第1 個擾動策略，否則則執行第2 個擾動策略。重復上述過程，但所有擾動策略執行完畢后，則VNS 的過程結束，該過程將輸出優化后的解。

五、算例分析及討論

為了驗證本方法的性能，通過模擬產生100 個仿真場景。具體而言，隨機產生一組客戶集合（包括客戶的數量、客戶的位置、客戶取送貨重量、客戶的時間窗）、配送中心的位置以及車輛最大數量。同時，為便于比較，引入標準遺傳算法作為比較基準。為了減少誤差，對于每個仿真場景，都用兩種算法分別運行30 次，并對這30 次結果取平均值（如圖7）。

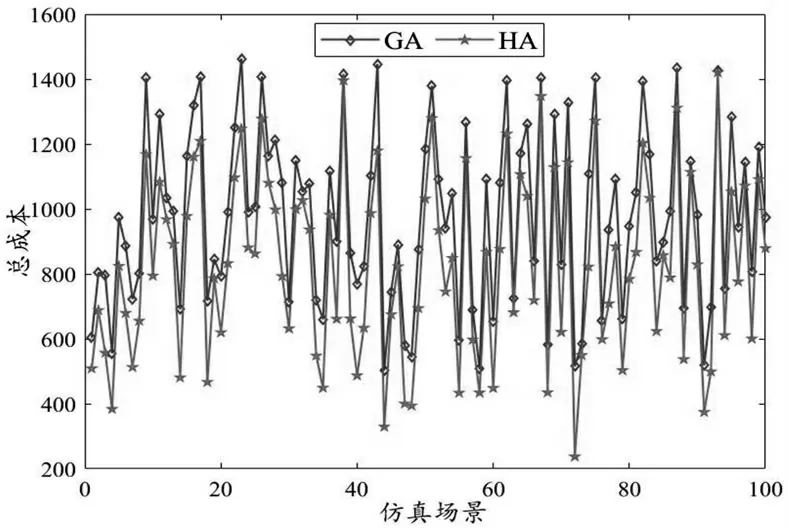
圖7 兩種算法總成本對比

為了探索兩種方法的性能是否有統計學意義上的差異，使用配對樣本t 檢驗的方法對二者的結果進行進一步分析。檢驗結果分別如表2 和表3 所示：遺傳算法得到的總成本均值為978.74，標準偏差為271.30，而啟發式方法得到的成本均值和標準偏差分別為823.82 和280.96，t（100）=23.90，p＜0.05，說明在0.05 的顯著性水平下，相比于遺傳算法，啟發式方法得到的總成本顯著較低。

表2 描述統計（遺傳算法Vs.啟發式方法）

表3 配對樣本t 檢驗結果（遺傳算法Vs.啟發式方法）

六、研究總結與展望

近年來，我國電子商務的快速發展帶動了快遞行業的發展，相應地也加劇了該行業的競爭。 “ 最后一公里 ” 作為電子商務物流活動的最后環節，在提升物流效率、降低物流成本和提高服務滿意度等方面具有重要意義；與此同時， “ 最后一公里 ” 同樣也面臨眾多問題和挑戰。

“ 最后一公里 ” 整合正逆向物流的車輛優化問題，被抽象為一個VRPSPDTW，設計一個基于遺傳算法和變鄰域搜索算法的3 步驟啟發式方法來求解該問題。通過構建100 個仿真場景，并通過統計分析的結果驗證了該啟發式方法具有較好的性能。

盡管所設計的啟發式方法能夠較好地解決同時取送貨的帶有時間窗的車輛路徑規劃問題，但是隨著客戶規模的增加，算法的效率還有待提升。除此之外，由于交通擁擠、等待客戶等情況時有發生，這就使得將交通時間和服務客戶時間視為確定值往往與實際情況不符合。因此，未來在研究 “ 最后一公里 ” 物流車輛路徑優化時，需要進一步考慮這些隨機因素。

注釋：

①數據來源：國家統計局.