點的兩類定義下的運動與變形分析

李宏德

（鄭州工程技術學院機電與車輛工程學院，鄭州 450044）

“點”是一個抽象模型，在剛體力學和變形體力學中的含義有明顯不同. 同時，力學中許多概念如關于點的運動、應力、應變的定義均是基于點來表述的. 文獻［1-3］中文章分析了點的兩類定義，對兩類定義作了對比研究，進而辨析了點的運動、應力、應變等問題.

1 點的概念

關于點，圍繞形狀和大小，有兩種類型的定義，一類是大小為0 的幾何點（幾何存在），另一類是大小為非0 無窮小的微元. 要弄清點的這些不同特性，需要辨清“0”和“無窮小”兩個相關概念，并分析其與點的關系.

1.1 0與點的第一類定義

1.1.1 0的認知 要認知“點的大小為0”，需分析0的性質.

前十個自然數中，0出現最晚. 0始于古印度，印度大乘佛教中有“一切皆空”、“絕對無”、“空無”這樣的宗義，被認為具有發明0的思想基礎. 早期的0不具有數值意義，僅用作占位符號，用于標識位置. 印度數學家婆什伽羅第一個用圓圈表示零. 婆羅摩笈多第一個把零作為數字進行描述，給零以量的含義，并描述了零的算術性質［4-6］.

在量的意義上，0是最小的自然數，有確切的數值含義，是正負數的界標，在數軸上或坐標系上具有確切的位置. 漢語中與0在量的語義上相近的“零”，就有表示沒有數量的意思，印度-阿拉伯數字中，0也表示“沒有”，并作為獨立的數字參與運算. 而在幾何上，0不具有與之對應的幾何圖形，這應理解為0是沒有形狀概念的［7］.

可見，起初0僅用作占位符號，具有標識位置的意思. 之后，作為數字的0，其數值意義是“無”.

1.1.2 點的第一類定義 在此，把大小為0的點作為點的第一類定義. 在幾何上是無形狀的幾何存在.

點的基本解釋為數學上指沒有長寬高而只有位置的不可分割的幾何圖形. 文獻［8］可以理解為點具有這樣的性質，一是無大小，二是無形狀，三是存在且具有位置. 較早的關于點的學術性定義是源于歐幾里得的《幾何原本》：“點是沒有部分的東西”. 沒有部分，即不可分成兩部分，或不可再分為更小的東西［9］. 引申認為點是沒有大小的，或說點的大小為0. 數學家丹尼·亨利翁注釋點是“沒有長度、沒有寬度、沒有高度的幾何形狀”. 文獻［9］中德國數學家戴維·希爾伯特在《幾何基礎》中沒有給出點的定義，把點、直線和平面作為不加定義的基本概念. 但點的屬性仍是無大小、不可分的. 文獻［10］二維歐氏空間中，點可表示為一組有序數對；笛卡爾坐標系中，點可以精確定義位置；微積分定義空間的點是一個0維的對象. 物理學和剛體力學對質點（點）的定義大致相同，認為點是沒有大小和形狀，但具有物體的全部質量. 忽略物體的大小和形狀，而將其抽象為一個有質量而無大小和形狀的幾何點. 可以進一步認知微元ΔV上的內力對ΔV內任一點的力矩都等于0［11-13］.

可見，點是沒有形狀的幾何存在；點的大小等于0. 應明確，此點其大小是0而不是無窮小. 就點的運動分析而言，點是濃縮的點或整體被視為點，即把有限濃縮于0，是沒有部分的.

1.2 無窮小與點的第二類定義

1.2.1 無窮小 極限是指不可逾越的數值，它是一個無限的變化過程，是變量的歸宿. 無窮小是一個以0為極限的函數，也是一個變化過程，它的歸宿是0. 文獻［14］中從0 到無窮小的躍遷體現了從無到有的質變. 微積分中定義，如果函數f(x)當x→x0（或x→∞）時的極限為零，那么稱函數f(x)為當x→x0（或x→∞）時為無窮小［15-16］.

可見，無窮小是以0為極限的；它不是0；它比任意給定的數都要小，需要多小就有多小. 應明確，無窮小不是很小很小的數；極限和無窮小都不能作為靜止的量來對待.

1.2.2 點的第二類定義 在此，把大小為非0無窮小的點作為點的第二類定義. 在幾何上是一個微元.

微積分中，從鄰域的概念來認知點. 鄰域是這樣一種集合，設a、δ 是實數且δ＞0，定義點a的δ 鄰域，記作U(a,δ)，為下列集合：U(a,δ)={x || x-a |＜δ }. 文獻［14］進一步設想，如δ是任意給定的極小正數，其小的程度沒有限制，那么，這個鄰域的極限就用來表述點. 還可以從空間向量上認知點，它是一個0維的向量空間.變形體力學認為，圍繞一個點取微元（一維、二維或三維），當描述該微元的尺度從對應方向上都趨于無窮小時，微元即視為點. 文獻［17］可以進一步引申，微元ΔV上的內力對ΔV內任一點的力矩一般都不等于0，只是力矩很小.

可見，這里的點是沒有確切形狀的微元，或者說可以取任意形狀；點的大小不是0. 就應力應變分析而言，點是取出的實際點或實際單元，是沒有被縮脹的點，點的應力應變分析是在從整體上取出的一個點上進行的，是整體中的部分.

2 點的運動——基于0的點的運動

點的運動是基于點的第一類定義的. 在此，點是大小為0的幾何存在. 研究這類點的幾何位置隨時間變化的規律，描述運動的參數只有線運動量沒有角運動量. 反映在運動軌跡上是直線的或曲線的；反映在速度上是線速度，而無角速度；反映在加速度上是切向加速度和法向加速度，而無角加速度.

對于點的合成運動，絕對運動和相對運動是點分別相對于定系和動系的運動，兩者都是點的運動，應遵從點的運動特征和運動規律，分析運動的參數只能用表征點的運動的參數來表述. 牽連運動是動系相對于定系的運動，是剛體運動而非點的運動，分析運動的參數只能用表征剛體運動的參數來表述，其可能的運動形式是平移、轉動或其他較復雜的剛體運動. 進一步推及到剛體的平面運動，在引入基點的定義之后，剛體平面運動則分解為隨基點的平移和繞基點的轉動，剛體平移按點的運動來分析，繞基點的轉動則按剛體瞬時的定軸轉動來分析.

3 點的應力應變——基于無窮小的點的應力應變

應力應變分析是基于點的第二類定義的. 在此，點是大小為非0無窮小的微元.

3.1 點的應力

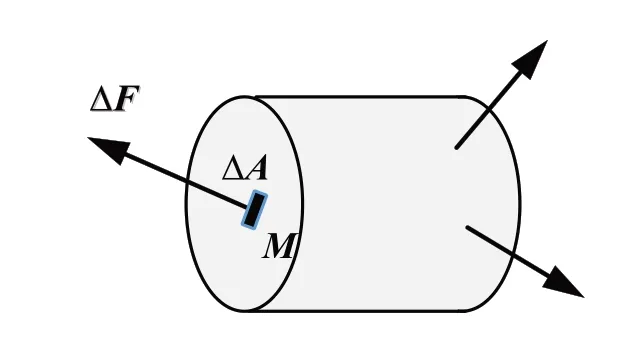
圖1 微面積及其內力Fig.1 Micro-area and its internal forces

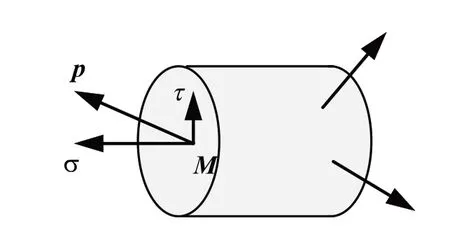
圖2 點的正應力和切應力Fig.2 The normal stress and shearing stress at a point

3.2 點的切應變

物體受力變形，體內各點處的變形并不相同，其變形程度由線應變ε 和切應變γ 來度量.

切應變γ 指兩條正交線段的夾角的改變量，定義γ為點在x-y平面內的切應變. 先分析平面的存在，根據幾何學，兩條相交線段組成平面，切應變即反映這兩條正交線段夾角的改變情況，它發生在由這兩條正交直線組成的平面內. 該平面其大小為非0的無窮小，在幾何上就是一個微面積，應從該面上來分析直角的改變量. 同理，從點的視角分析切應變，當兩條正交線段的長度趨近于0時，該平面的大小以0為極限，平面趨近于點. 所以，切應變是以點度量的.

切應變是由切應力引起的，切應力互等定理決定切應力的作用方式. 相鄰的正交面上的切應力不能單獨存在，是成對生成并作用的，實際上是兩對滿足互等定理的切應力在共同產生作用，在這兩對切應力作用的相關平面上，產生對應的切應變. 所以，切應變不是某一個切應力單獨作用的結果，而是互等定理構架內的所有切應力共同作用的結果，如圖3所示.

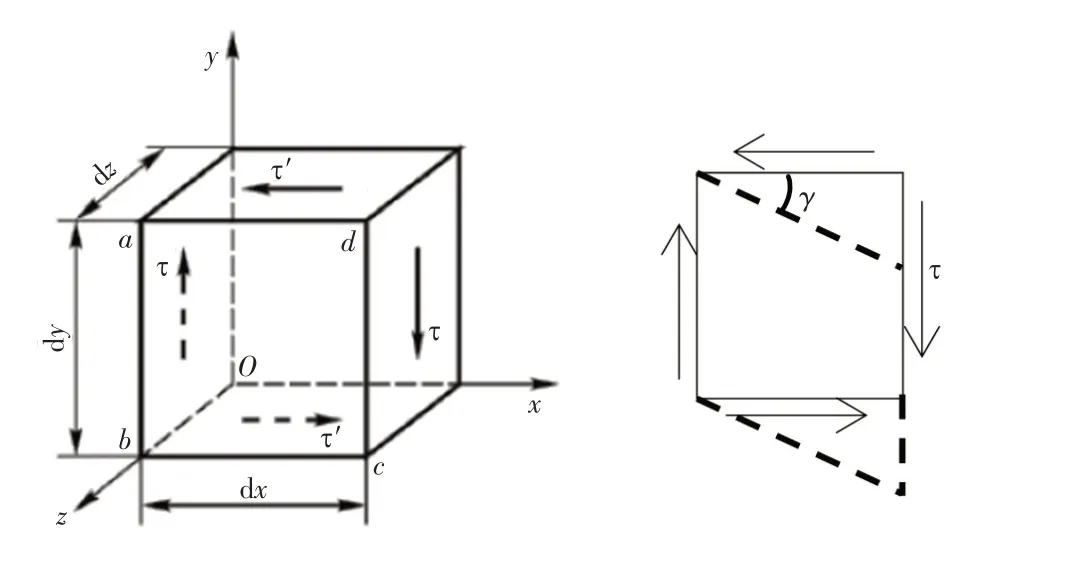
圖3 點的切應力與切應變Fig.3 The shearing stress and shearing strain of point

4 結論

文章辨析了基于0和基于無窮小的關于點的兩類定義的具體差異，并基于點的不同定義，深入分析點的運動、點的應變等問題，為準確認知相關概念提供借鑒.