稀疏超越指數追蹤的分位數回歸模型及其算法

范青竹， 張成毅， 羅雙華

（1.西安工程大學理學院，西安 710048； 2.西安交通大學經濟與金融學院，西安 710049）

在金融市場中，指數型基金的管理變得日益重要. 為了更加有效地研究投資組合問題，許多學者越來越關注指數追蹤［1］和超越指數追蹤［2］. 相比較指數追蹤，超越指數追蹤能夠在保證追蹤組合的收益率與標的指數收益率盡量一致的條件下給投資者帶來超額收益，即戰勝市場.

對于超越指數追蹤模型的建立和求解，國內外許多學者已經做了很多有意義的工作. Dose等［3］建立并求解追蹤誤差與超額收益的加權超越指數模型；Beasley等［4-5］建立一個混合整數規劃的超越指數模型，對模型采用兩階段逼近和三階段逼近求解模型；Lejeune等［6］和Guastaroba等［7］分別建立了一個凸二次錐規劃的超越指數模型和混合整數規劃的超越指數模型；胡春萍等［8］建立了時間加權SVM的指數優化復制模型，并利用OR-Library 中的5 個市場指數歷史數據進行實證檢驗；在利用元啟發智能算法求解模型方面，差分進化算法、免疫算法、混合遺傳算法給出了很好的求解思路［9-11］；馬景義等［12］構建了一個可以調節追蹤誤差和超額收益的超越指數模型，并給出了廣義最小角度回歸算法；趙志華等［13］提出了交替二次罰算法的稀疏超越指數追蹤模型，該模型用二次罰算法（AQP）求解.

由上可知，超越指數追蹤已經取得了長足的進步，這主要得益于稀疏優化［14-16］的發展. 目前對超越指數追蹤問題的研究大多是基于均值回歸的最小二乘模型，但由于風險資產收益數據的非對稱性和尖峰厚尾的非正態分布特征，使得超越指數追蹤的投資組合穩定性較差. 為了解決這一問題，引入分位數回歸模型，分位數回歸由Koenker和Basset［17］提出，基于分位數回歸模型的靈活性及能夠對響應變量的條件分布作出全面描述而且不會受到異常值的影響，因此更加穩健也更加有效［18-20］. 利用分位數回歸模型研究超越指數追蹤問題具有重要的理論意義和應用價值.

1 稀疏超越指數追蹤的分位數回歸模型

1.1 超越指數追蹤

超越指數追蹤是在金融市場的N 個資產中選取其中的r 個構建成一個投資組合，超越指數的目標函數是最小化跟蹤誤差（TE）和最大化超額回報（ER），表示為

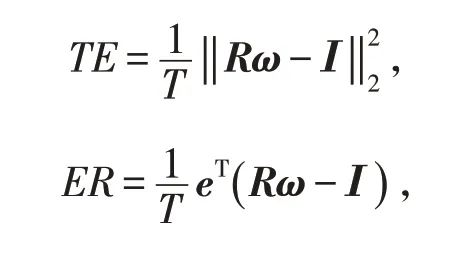
其中：R ∈?M×N和I ∈?M分別是N 個資產的收益率矩陣和每一個周期所有資產的收益率組成的向量；ω ∈?N是投資組合的權重向量；T 是選取總資產的期數；e 是一個全一向量；eT是e 的轉置. 因此，超越指數始終是TE 和ER 之間的權衡. 通過權衡參數給出混合單目標函數

其中：a 是追蹤組合與指數之間收益率差異的懲罰參數，a ∈( 0,1) .

1.2 分位數回歸模型

設定Xn×m=( x1,…,xm)是包含解釋變量的設計矩陣，我們要研究的線性模型是

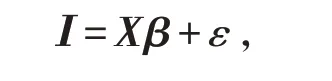
其中：I 每一個周期所有資產的收益率所得到的中位數組成的向量；β 是回歸系數向量；ε 是隨機誤差項.

分位數回歸主要是最小化目標函數

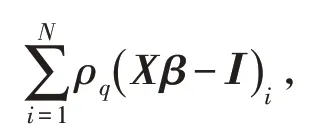
其中：

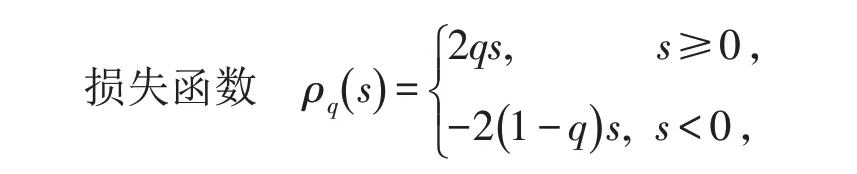
對于任意的實數s 都成立，其中q 是分位數，q ∈( 0,1) .

考慮模型（1）式構造分位數回歸的超越指數追蹤模型

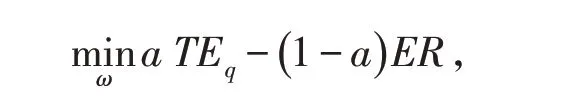
其中

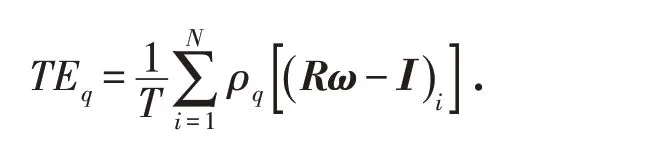
1.3 稀疏超越指數追蹤的分位數回歸模型

稀疏優化模型能夠用盡可能少的股票獲得盡可能高的超額收益. 用L1/2正則化模型構造分位數回歸的超越指數追蹤模型是因為L1/2正則化能夠產生更稀疏的解，在同等效果下能減少交易費用和交易成本.

因此建立一個稀疏超越指數追蹤的分位數回歸模型，模型如下：

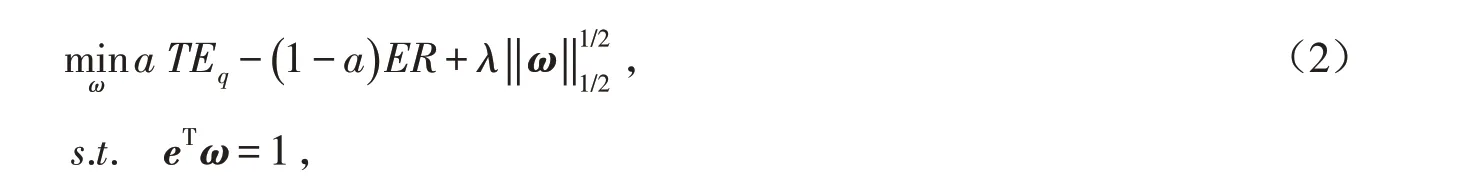
其中：λ 是正則化系數，λ ＞0.

2 HSS-Half閾值算法

利用凸優化中拉格朗日方法求解模型（2）為以下目標函數

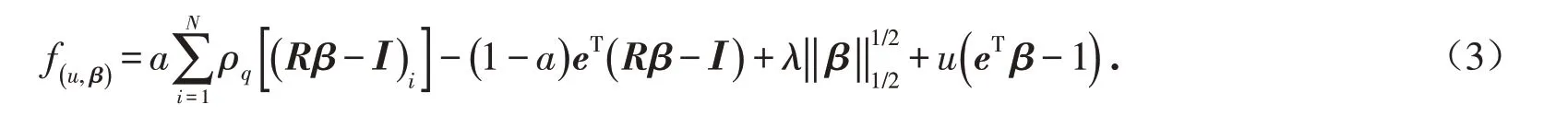
對于上式，分別對u，β 求導可得

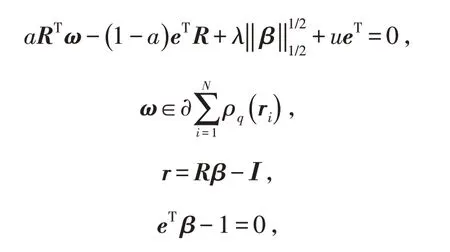
其中：u 是拉格朗日乘子；β 是回歸系數向量；a 是懲罰參數；ρq是損失函數；R 是收益率矩陣；I 是每一個周期所有資產的收益率所得到的中位數組成的向量；e 是一個全一向量；λ 是正則化系數；r 表示股票收益率向量.

函數ρq的次微分為

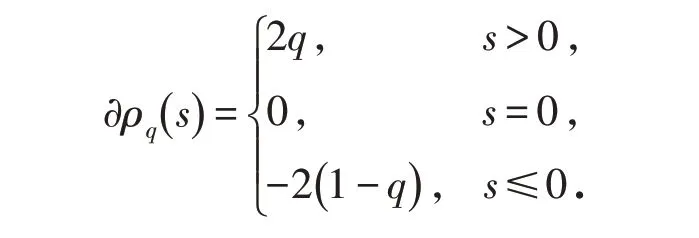
把u，β 求導后寫成矩陣的形式：

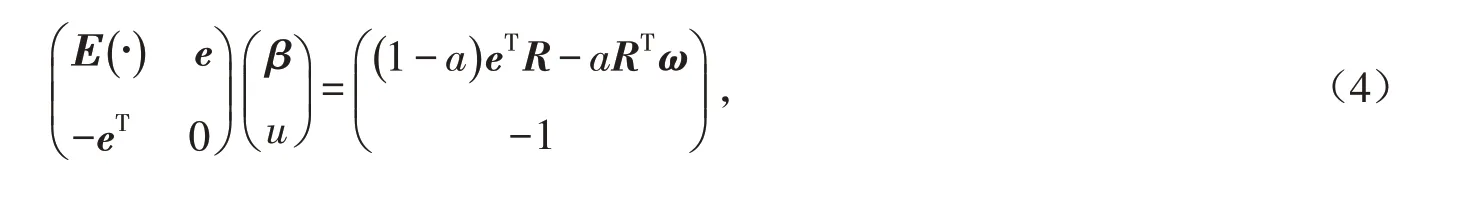
其中：

令

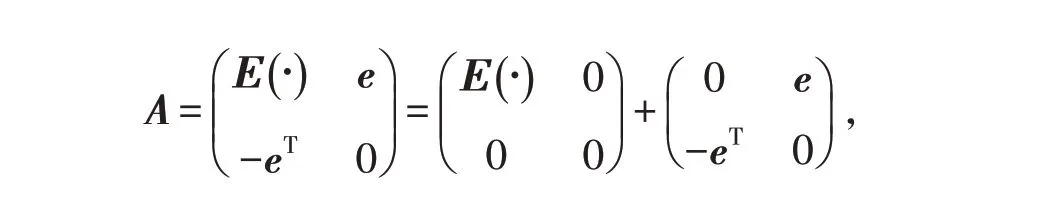
不改變A 的大小作如下變換得

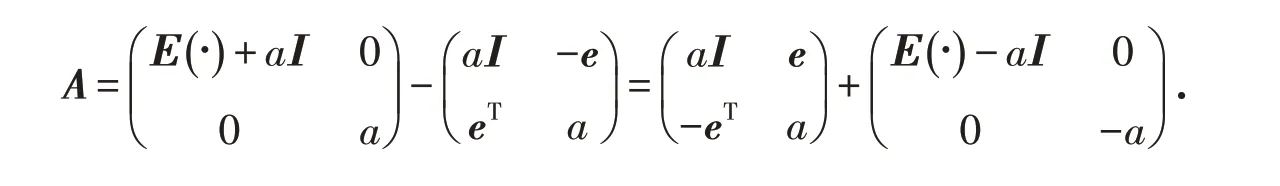
所以（4）式可表示為

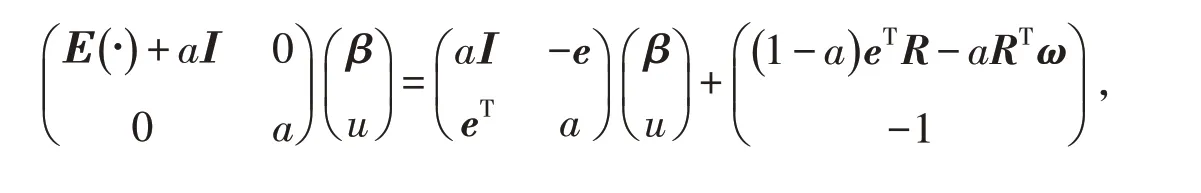
可推出：

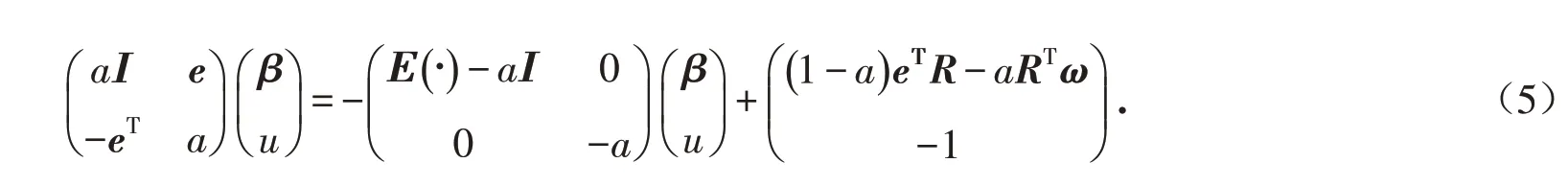
由上述等式可構造HSS迭代格式如下：

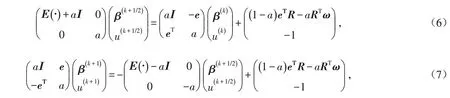
其中：k 是迭代次數. 對于迭代（6）式

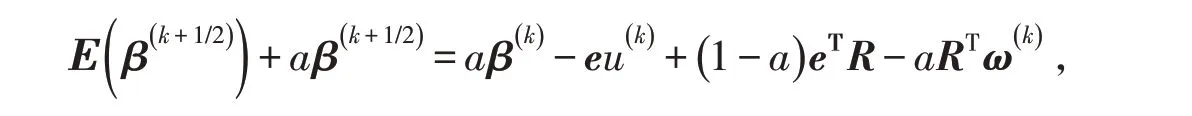
令

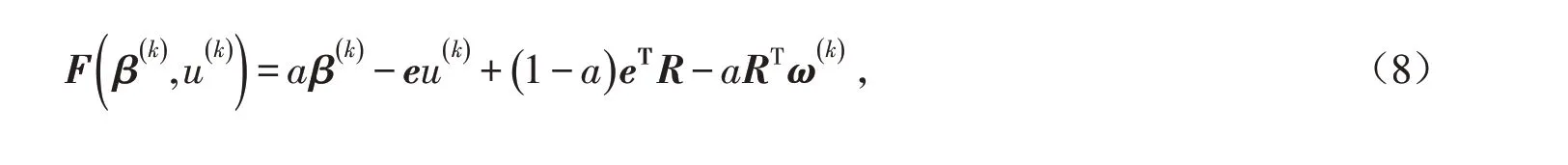
則有

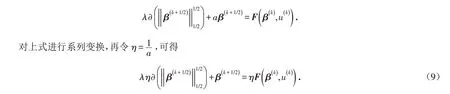
定義變量

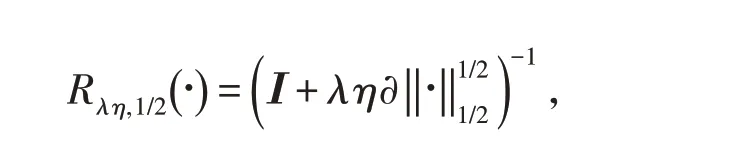
對（9）式做變換有以下迭代格式

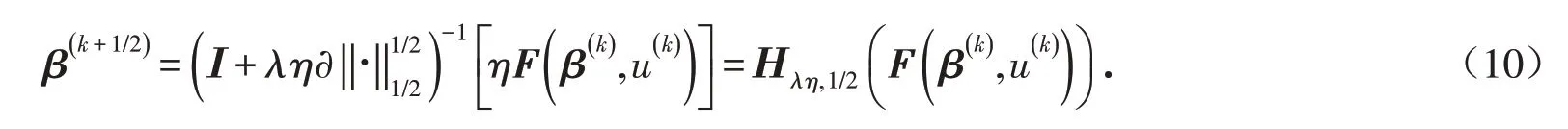
因此有以下迭代格式

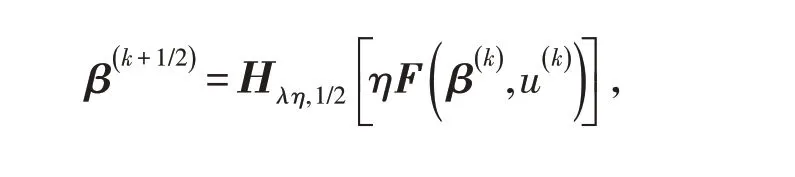
其中：

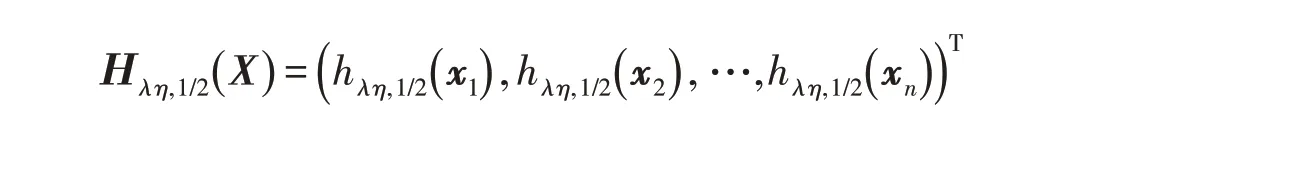
是Half閾值算子，

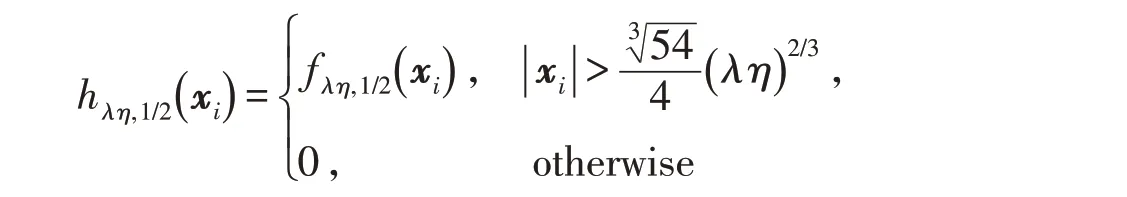
被稱為Half閾值函數，

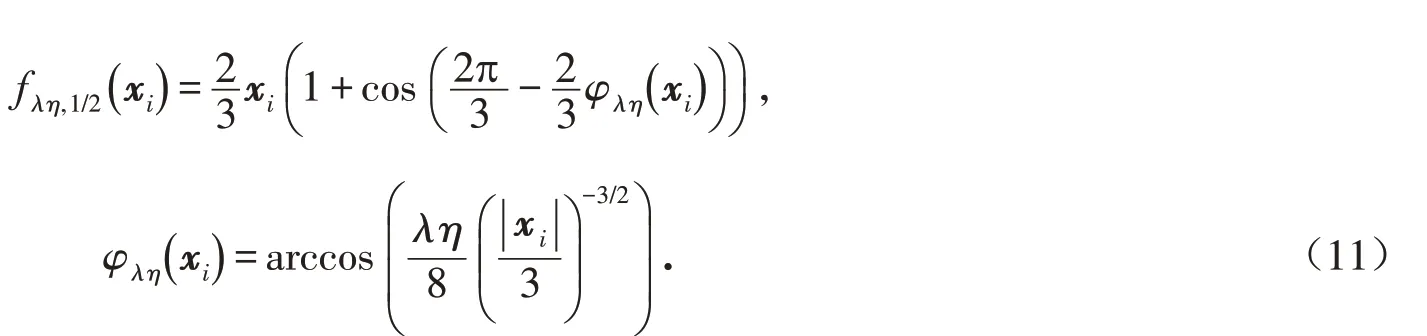
所以，HSS-Half算法的迭代（6）式為

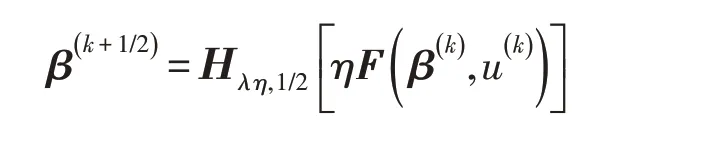
和

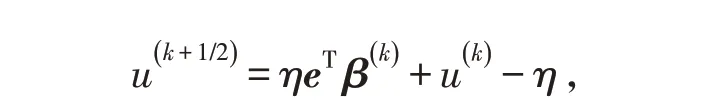
這樣就簡化了HSS-Half算法中（6）式的迭代格式，并得到新的等價迭代格式

3 實證分析

在本節選擇與文獻［13］中的稀疏超越指數追蹤模型進行對比，把稀疏超越指數追蹤模型記為模型A，把稀疏超越指數追蹤的分位數回歸模型記為模型B. 不比較兩種算法的快慢，只比較模型的優越性和樣本內外的一致性.

實證分析的數據包括金融數據庫OR-Library 中的恒生指數（香港），DAX 100 指數（德國），FTSE 100 指數（英國），S&P 100 指數（美國）1992—1997 年的290 個周收盤價構成數據集. 對于相應的指數和股票的290 周每周收益率，將前145周作為訓練數據集也就是樣本內數據集，后145周作為測試數據集也就是樣本外數據集. 對稀疏超越指數追蹤的分位數回歸模型進實證分析. 具體計算中，投資規模r 分別取5，10，15，20，25五種情況，懲罰參數a=0.8，分位數q=0.4，將兩種模型在樣本內外的一致性和優越性上進行比較.

為了度量樣本內外性質和樣本內外的一致性，引入以下兩個標準.

1）一致性. 定義A 產生的投資組合的樣本內和樣本外追蹤誤差的一致性為

其中：TEIA和TEOA分別為模型A 的投資組合的樣本內和樣本外的追蹤誤差. Cons( A) 的值越小，說明模型A 產生的投資組合樣本內和樣本外追蹤誤差的一致性越好.

2）樣本外優越性. 我們定義

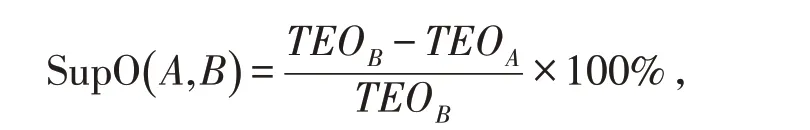
其中：TEOA和TEOB分別是模型A 和模型B 對組合的樣本外追蹤誤差. 如果SupO( A,B )＜0，則TEOB小于TEOA，即模型B 的投資組合在樣本外追蹤誤差方面優于模型A .

表1、2、3中N 是數據集中資產數目，ERI，ERO 分別表示樣本內超額收益和樣本外超額收益.

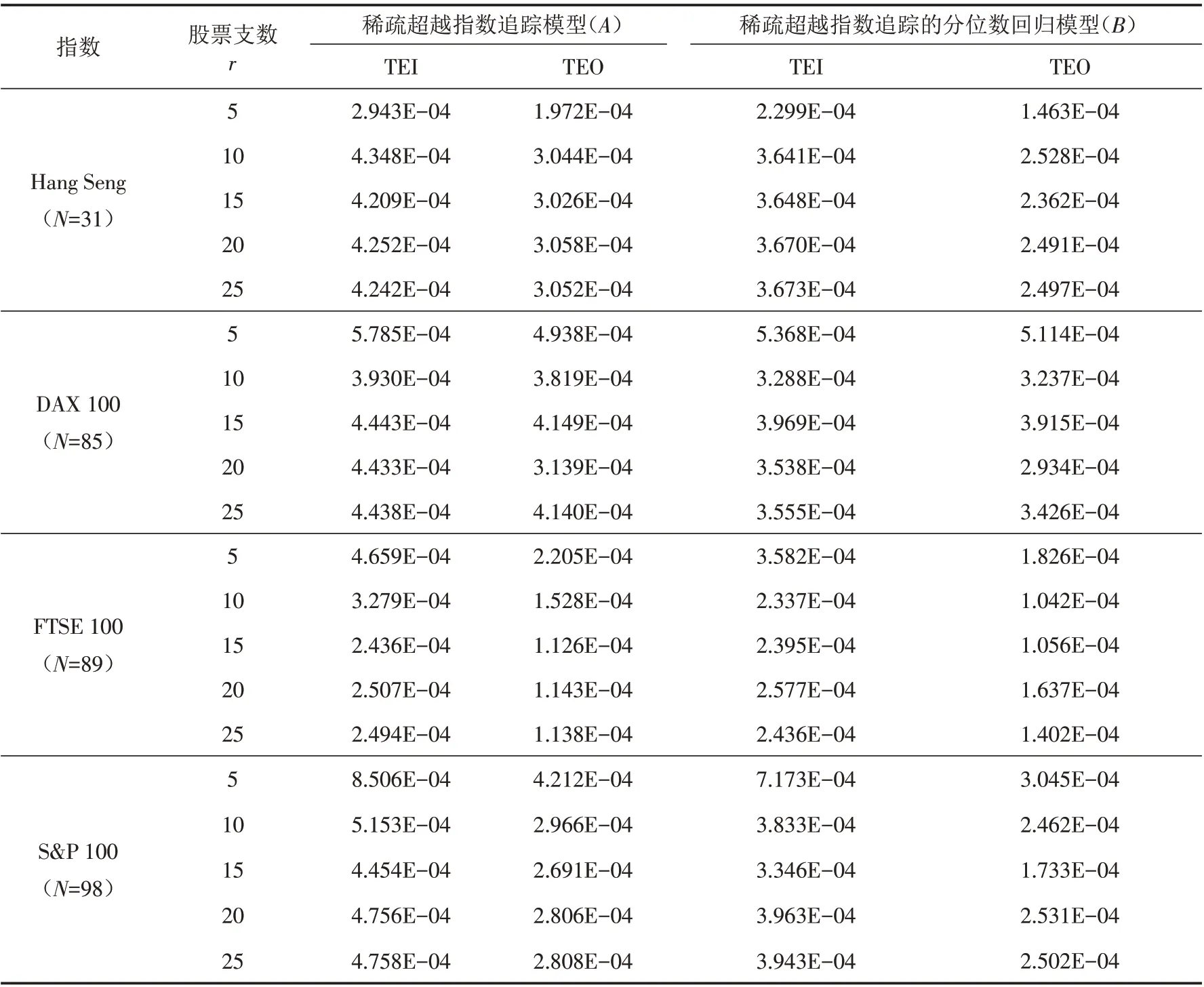
表1 兩個模型在樣本內外誤差的對比Tab.1 Comparison of in-sample and out-of-sample errors between the two models

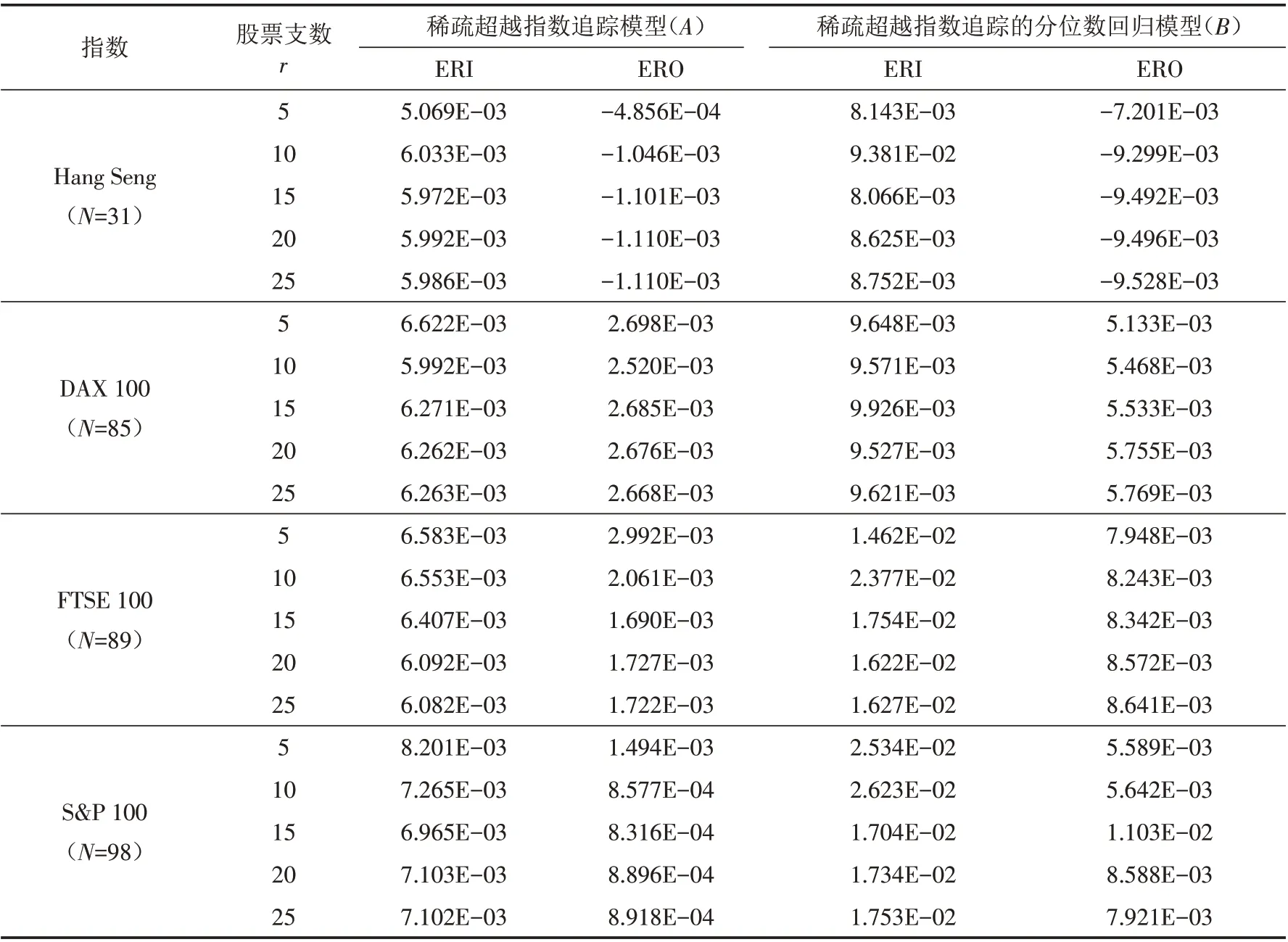
表2 兩個模型在樣本內外收益的對比Tab.2 Comparison of in-sample and out-of-sample returns between the two models

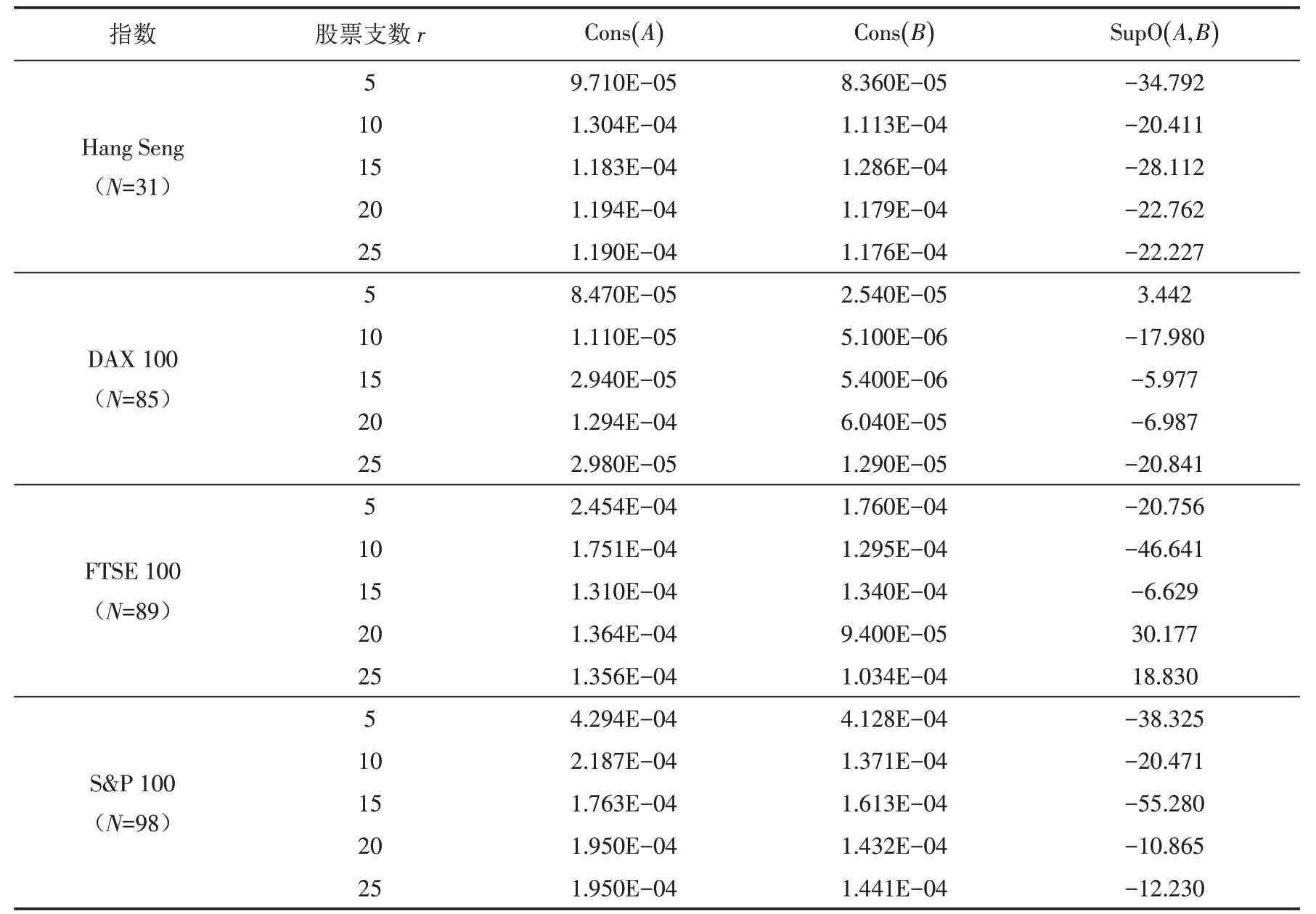
表3 兩個模型在樣本內外的一致性和優越性的對比Tab.3 Comparison of consistency and superiority of the two models with in-sample and out-of-sample

表1是兩個模型分別在樣本外和樣本內的追蹤誤差，可以看出模型B 比模型A 在樣本內和樣本外的誤差更小. 表2是兩個模型分別在樣本外和樣本內的超額收益，可以看出模型B 比模型A 在樣本內和樣本外的超額收益更大. 從表3可以看出：①模型B 在樣本內外誤差之間的一致性比模型A 更好，因為90%（18/20）實例的Cons( B )＜Cons( A) ；②模型B 的投資組合在樣本外追蹤誤差方面優于模型A，因為85%（17/20）實例的SupO( A,B )＜0，這證明了模型B 在測試集上的表現更好.

綜上所述，稀疏超越指數追蹤的分位數回歸模型與稀疏超越指數追蹤模型相比，不僅誤差風險更小，并且能夠獲得更好的超額收益.

4 結語

在超越指數追蹤模型的基礎上進行優化擴展，通過引入分位數回歸模型和L1/2正則化理論建立了稀疏超越指數追蹤的分位數回歸模型，其求解算法HSS-Half閾值算法具有良好求解能力. 稀疏超越指數追蹤的分位數回歸模型具有較好的穩健性和適應未來風險的能力.