利用壓裂停泵數據的大規模體積壓裂改造區域反演方法及其應用

張忠林，申 峰，徐棟哲，李清宇

(1.陜西延長石油(集團)有限責任公司，陜西西安 710075；2.中國科學技術大學，安徽合肥 230027；3.中國科大-延長石油聯合實驗室，安徽合肥 230026)

以頁巖油氣為代表的非常規油氣藏受到了國家的高度關注[1-2]。非常規油氣儲層十分致密，只有通過大規模體積壓裂技術才能實現工業產能[3-4]。大規模壓裂后將形成復雜的縫網，是油氣藏開發的重要保障。與大規模體積壓裂的廣泛應用形成鮮明對比的是，對壓裂效果的評價一直是一個難題。目前大規模體積壓裂改造區域(SRV)面積[5]以及裂縫半長是評價壓裂效果最直觀的兩個參數，現有的壓裂效果評價方法也是圍繞著如何獲得準確的SRV面積和裂縫半長而展開的。

我國頁巖油氣普遍埋深在2 000～5 000 m，這導致地層中的流動模式無法通過直接觀察測量的手段來獲得。目前通用的大規模體積壓裂效果評價方法可以分為裂縫監測方法和參數反演方法。裂縫監測方法主要包括微地震[6]和微電位[7]方法，這兩種方法都存在施工難度大、成本高昂(單井次僅施工成本即達數百萬元)的問題。

壓力數據參數反演方法[8]是目前常用的低成本壓裂效果評價方法，主要包括試井分析方法[9]、壓前小型壓裂測試技術[10]、G函數分析[11]、Nolte線性流分析、Nolte徑向流分析和Soliman/Craig徑向流分析等[12]，這些方法主要是通過操作人的經驗，不斷調整裂縫參數和曲線形態來獲取裂縫參數。但是水平井多段壓裂擬合反演十分困難、耗時，且存在嚴重的多解性問題。

國際上很多學者都提出了SRV區域反演相關方法[13]。Zhao等在傳統的多段壓裂水平井的基礎上提出了一個復合油藏模型，該模型可用于描述由于水力壓裂引起的SRV區域的特征[14]。Fan等研究了致密油氣藏中SRV區域尺寸對壓力瞬變特征的影響，通過壓力波到達邊界的時間可以反演出SRV區域的面積[15]。上述方法獲取的SRV區域面積及滲透率均為生產一段時間后的結果，缺乏足夠的時效性。

本團隊在前期工作中提出了基于數字濾波壓裂停泵數據反演方法，利用壓裂停泵數據進行裂縫參數反演，可以得到裂縫半長、改造區域滲透率等參數。但目前壓裂規模評價體系中，除裂縫半長外，SRV區域的形態和面積等同樣受到了極大的關注，因此，需要提出新的方法來計算和模擬大規模體積改造過程中形成的SRV區域。

本文旨在基于數字濾波壓裂停泵數據反演方法，提出非均質地層中多段壓裂水平井地層壓力分布的計算方法。利用壓裂停泵數據進行參數反演，不僅可以得到裂縫半長、地層滲透率等重要參數[16-17]，而且可以獲得SRV區域面積等參數，大大降低施工成本的同時，獲取到更多地層信息。由于目前非常規油氣藏開發都要進行大規模體積壓裂改造，至“十三五”末，為實現“十三五”規劃的頁巖氣年產300×108m3，僅四川地區就要新鉆1 000余口水平井。為此，本文為我國深部資源開發提供大規模體積壓裂效果評價方法，具有廣闊的應用前景。

1 大規模體積壓裂改造區域反演方法

本文提出了壓裂停泵期間壓力能夠波及的范圍即為SRV區域的基本假設，運用紐曼乘積法與杜哈梅原理，開展壓裂施工過程中壓力在地層中波及范圍的理論推導工作，重點針對非均質地層首次給出其壓力分布的理論推導過程，并以此來反演大規模體積壓裂改造區域，是大規模體積壓裂改造區域反演的一種新方法。

1.1 SRV區域反演方法

考慮到實際情況下多段壓裂水平井地層通常具有較強的非均質性，本節重點研究了非均質地層中多段壓裂水平井壓力分布的計算方法。

本文作出如下假設：壓裂過程會產生一條主縫以及以縫網為主的改造區域。由于改造區域內的滲透率要明顯高于地層滲透率，因此壓力在SRV區域內的傳播速度要遠遠快于未改造的基質。基于上述假設和合理推論，本文認為在壓裂停泵期間，壓力能夠波及的范圍即為SRV區域。

基于上述理論，SRV區域可以通過計算壓裂施工過程中壓力在地層中的波及范圍來確定，其關鍵過程是首先推導出地層壓力分布隨時間變化的關系，然后對改造后的裂縫半長、地層滲透率及壓裂施工過程的壓力傳播時間等參數進行賦值，最終形成完整的SRV區域反演方法。因此，本節工作的核心內容可以簡化為3個部分：①非均質地層多段壓裂水平井地層壓力分布的理論推導；②改造后裂縫半長、地層滲透率以及壓裂施工過程中壓力傳播時間等關鍵參數的獲得；③SRV區域的反演計算方法。

1.2 多段壓裂水平井地層壓力分布的理論推導

1.2.1 拉普拉斯空間中的壓力分布理論解

首先對于全封閉均質矩形地層中一口多段壓裂水平井而言，利用紐曼乘積法可以計算井底壓力[18]。根據杜哈梅原理[19]，在拉普拉斯空間中無量綱流量與無量綱壓力應滿足下述關系：

(1)

(2)

上式中有

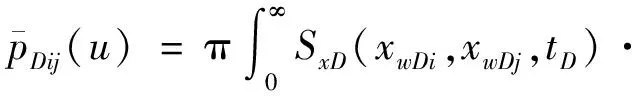
SyD(ywDi,ywDj,tD)e-utDdtD

(3)

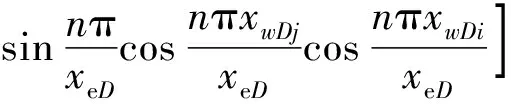
(4)

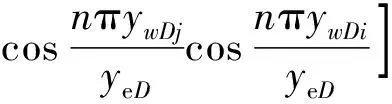
(5)

式中pwDi——在第i條裂縫處的無量綱井底壓力；

xfDi=xfi/L——無量綱裂縫半長；

pDij——第j條裂縫在第i條裂縫處產生的無量綱壓力影響；

xwDj，ywDj——第j條裂縫的位置；

xeD，yeD——地層的邊界大小；

u——拉普拉斯算子；

n——裂縫總條數。

其他相關無量綱定義可參考相關文獻[20]。

考慮到井儲效應和表皮效應，公式(1)～(2)可改寫為：

(6)

(7)

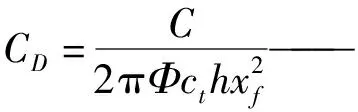
C——井儲常數；

S——表皮因子。

由于裂縫都與井筒相連，這里假設水平井筒內的壓力處處相等，基于式(6)～(7)，可以得到下述矩陣方程：

(8)

1.2.2 非均質地層中的壓力分布理論解

基于前人的工作和方法，我們在1.2.1節中考慮井儲效應和表皮因子，給出了均質地層的壓力求解矩陣。但是在實際的水平井壓裂施工過程中，會存在明顯的非均質性問題，這導致常規的均質地層壓力求解矩陣并不適用。因此，本文基于流度比的定義，考慮不同裂縫區域的滲透率變化情況，重構壓力求解矩陣，最終推導得到拉普拉斯空間中地層壓力分布的表達式。

考慮到壓裂改造后實際地層中會存在較強的非均質性，本文定義第1條裂縫區域的流度與第n條裂縫區域的流度比值為：

(9)

這里kn代表第n條裂縫區域的滲透率。我們可以看出，本文中定義的fn實際上就是流度比的倒數。

那么式(9)可以改寫為

(10)

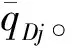
SyDj(yD,ywDj,tD)e-utDdtD

(11)

式中

(12)

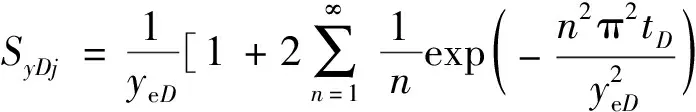
(13)

1.2.3 物理空間中的壓力分布

通過式(11)可以得到拉普拉斯空間上的壓力分布，通過拉普拉斯數值反演方法[27]，可以得到物理空間中的壓力分布：

(14)

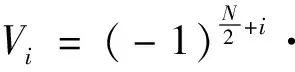
1.3 關鍵參數的獲得

根據公式(11)和(14)，我們得到了地層壓力分布隨時間的變化。通過對公式的解讀，為計算壓裂施工過程中壓力在地層中的波及范圍，需要知道如下參數：每段裂縫的位置、改造后的裂縫半長、地層滲透率以及壓裂施工過程中的壓力傳播時間。其中，裂縫位置可以通過井眼軌跡獲得，因此本節重點研究如何利用已有的壓裂停泵數據反演得到改造后的裂縫半長、地層滲透率并確定壓力傳播時間，可以大幅降低解釋成本。

1.3.1 改造后裂縫半長、地層滲透率的確定

傳統的解釋方法包括微地震方法和G函數分析方法等，但是這些方法存在解釋成本高、獲得參數有限的情況。課題組在前期工作中提出了基于數字濾波壓裂停泵數據反演方法，利用壓裂停泵數據進行裂縫參數反演[22]。圖1所示的壓力數據為壓裂施工后停泵期間記錄的壓降情況示意圖。該段數據記錄的是井口壓力，而且前期存在較為明顯的波動情況，也就是水錘效應。通過對壓裂停泵數據進行井口—井底壓力折算、數字濾波處理并進行圖版擬合，可以反演得到裂縫半長xf、地層滲透率k、表皮系數S、井儲常數C等重要參數。

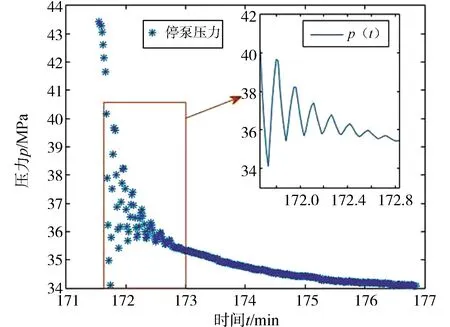
圖1 壓裂停泵數據示意圖

1.3.2 壓力傳播時間的確定

為計算壓裂施工過程中壓力在地層中的波及范圍，傳播時間是非常重要的參數。本節定義了壓裂施工過程中壓力傳播時間的概念，并根據滲流力學理論，結合壓降漏斗變化規律，給出了壓力傳播時間的確定方法。

根據滲流力學理論，壓裂施工停泵后會形成一個凸起型的壓力分布曲線，也就是一個反向壓降漏斗，如圖2所示。由于改造區域內的滲透率比較高，因此壓力分布曲線的前期變化速度會非常快。當壓力傳播到達SRV區域外邊界時，由于基質滲透率遠遠低于SRV區域內的滲透率，此時壓力傳播速度會大大減緩，相應的壓力分布曲線的變化速度將會非常緩慢。因此，可以認為，當監測到的停泵壓力降落速度突然減緩，壓力幾乎不再下降時，這個時刻就是壓裂施工過程中的壓力傳播時間。

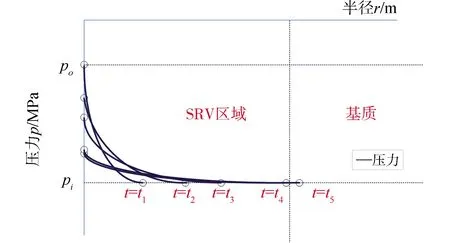
圖2 壓裂停泵時的地層壓力分布曲線

以圖3為例，可以看到停泵后壓力迅速下降，隨后下降速度逐漸變緩，5.5～6 h時壓力幾乎不再下降。此時可以認為壓力傳播到達了SRV區域外邊界。

圖3 某井的壓裂停泵曲線圖

1.4 SRV區域的反演計算

根據滲流力學理論和壓裂停泵數據分析，得到停泵期間壓力傳播的流動時間，然后利用壓裂停泵數據反演得到地層滲透率和裂縫半長等參數，基于式(14)，通過計算壓力分布就可以反演大規模體積壓裂SRV區域。

為了更直觀地將SRV區域呈現出來，本文通過繪制壓力分布圖的形式給出SRV區域示意圖。由于壓力分布變化在裂縫附近變化較快，在基質區域內變化很小，如果采用均勻分布的繪圖方式，在裂縫附近的壓力變化很難細致地描述，因此，本文采用裂縫局部加密的方式繪制地層壓力分布圖(圖4)。在y方向上，仍采用均勻劃分的方式；在x方向上，采用下述指數形式公式，在裂縫附近進行加密，如圖5所示。

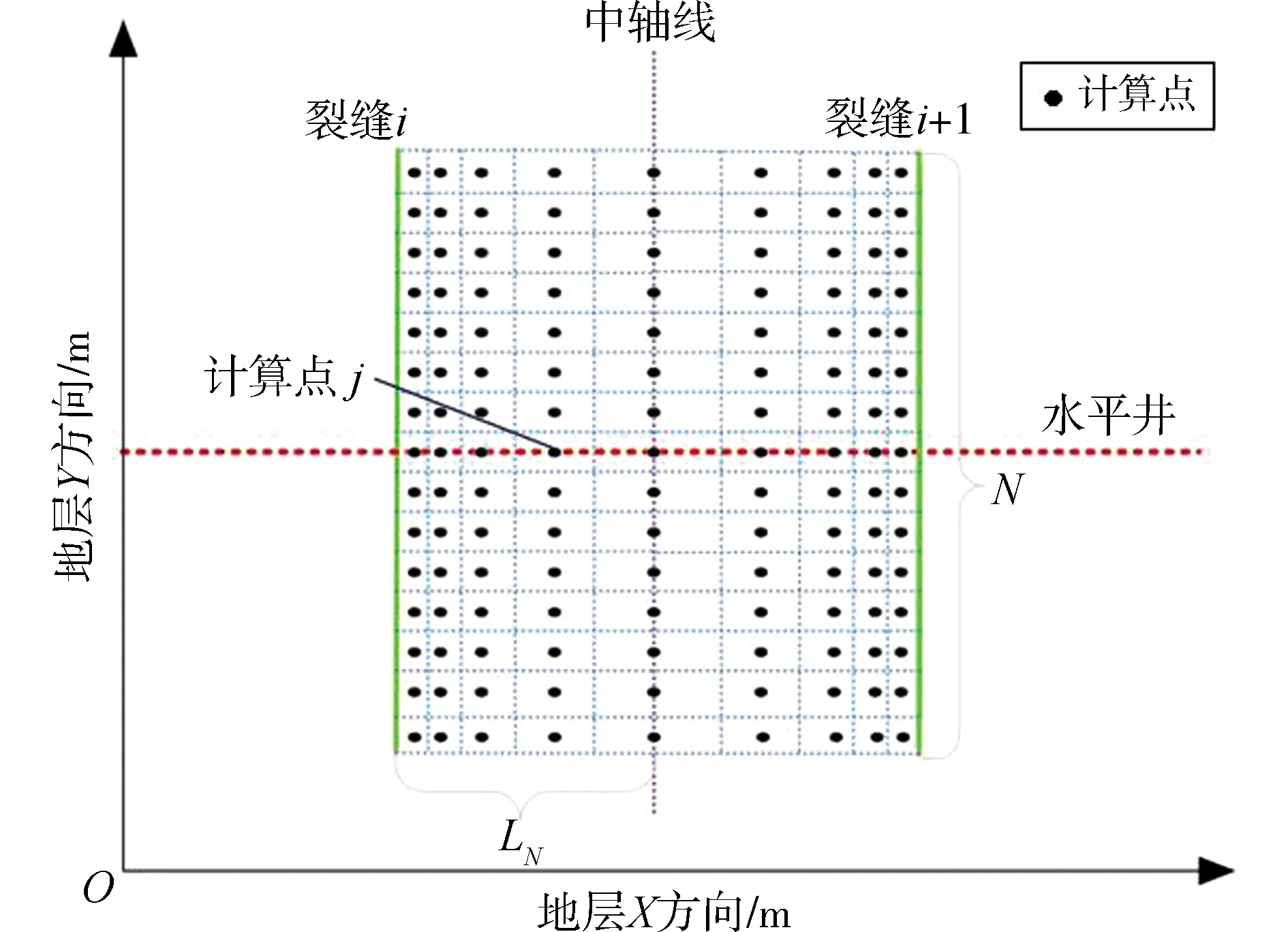
圖4 裂縫局部加密方法示意圖

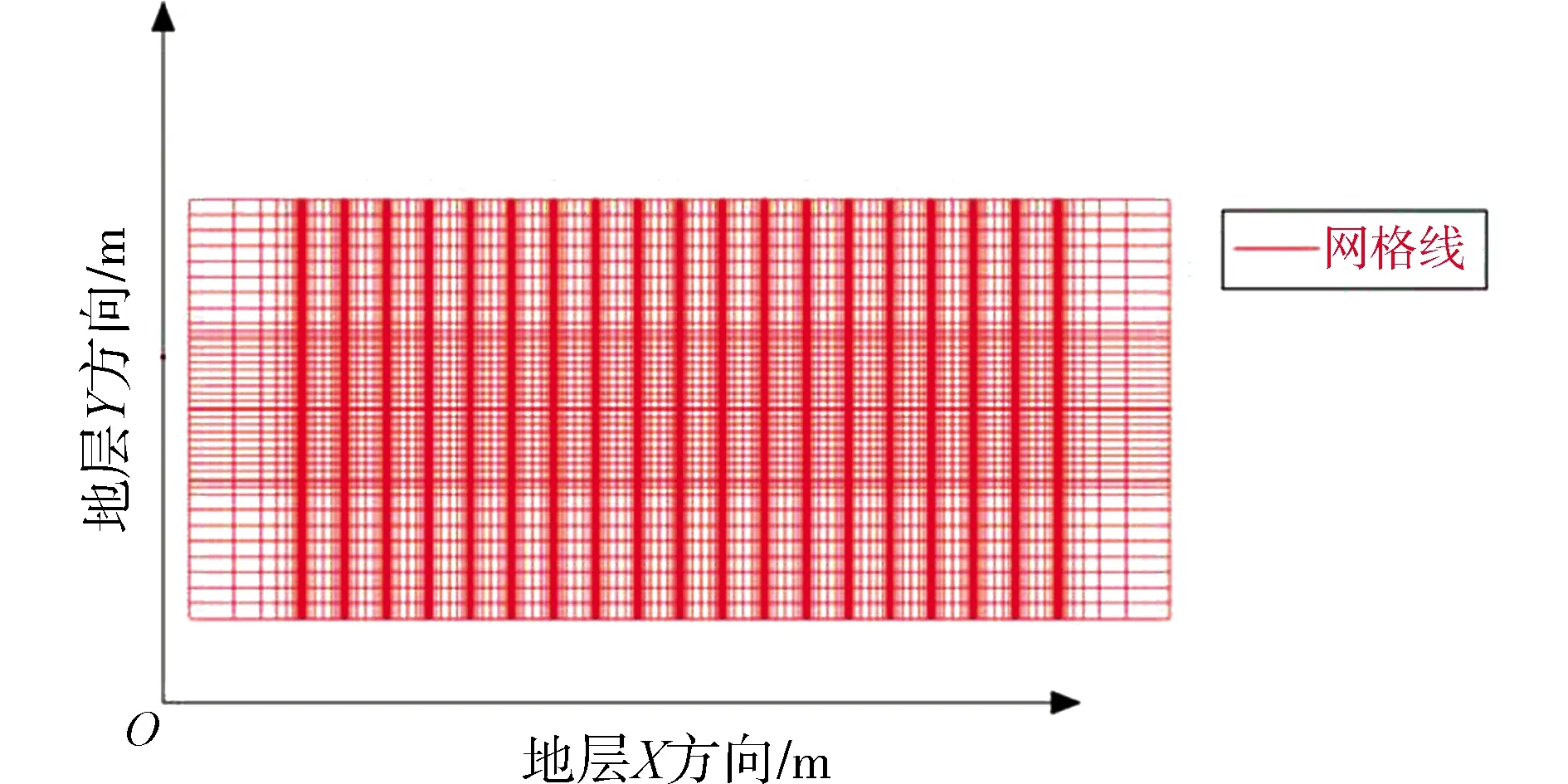
圖5 裂縫局部加密網格

(15)

式中Lref——特征長度；

M——x方向網格劃分個數；

Lw——兩條裂縫之間間距的1/2。

根據公式(11)、(14)和(15)，可以計算整個地層中每個節點的壓力數值，然后采用專門的畫圖模塊即可得到SRV區域示意圖。

2 實例分析

選取國內某頁巖氣區塊的一口多段壓裂水平井(下文簡稱示例井)的停泵數據進行解釋反演，共19段裂縫。水平井長1 650 m，射孔軌跡沿水平井均勻分布。采用數字濾波壓裂停泵數據反演方法，分別對每段裂縫進行數據反演。選取均勻流量垂直裂縫模型，對停泵壓降數據進行濾波處理，并在雙對數坐標系中繪制壓力數據和壓力導數數據的曲線，如表1和表2左側曲線所示。通過調整裂縫半長、滲透率，可以改變圖版曲線的形態。經過不斷地調整參數，最終可以使圖版曲線(實線)與實測數據(點線)達到最佳擬合情況，此時可以反演得到地層滲透率和裂縫半長。為了驗證壓裂停泵數據反演方法解釋結果的正確性，我們又與微地震數據進行了對比，表1和表2分別給出了第1段裂縫與第5段裂縫的裂縫半長與微地震結果的對比。

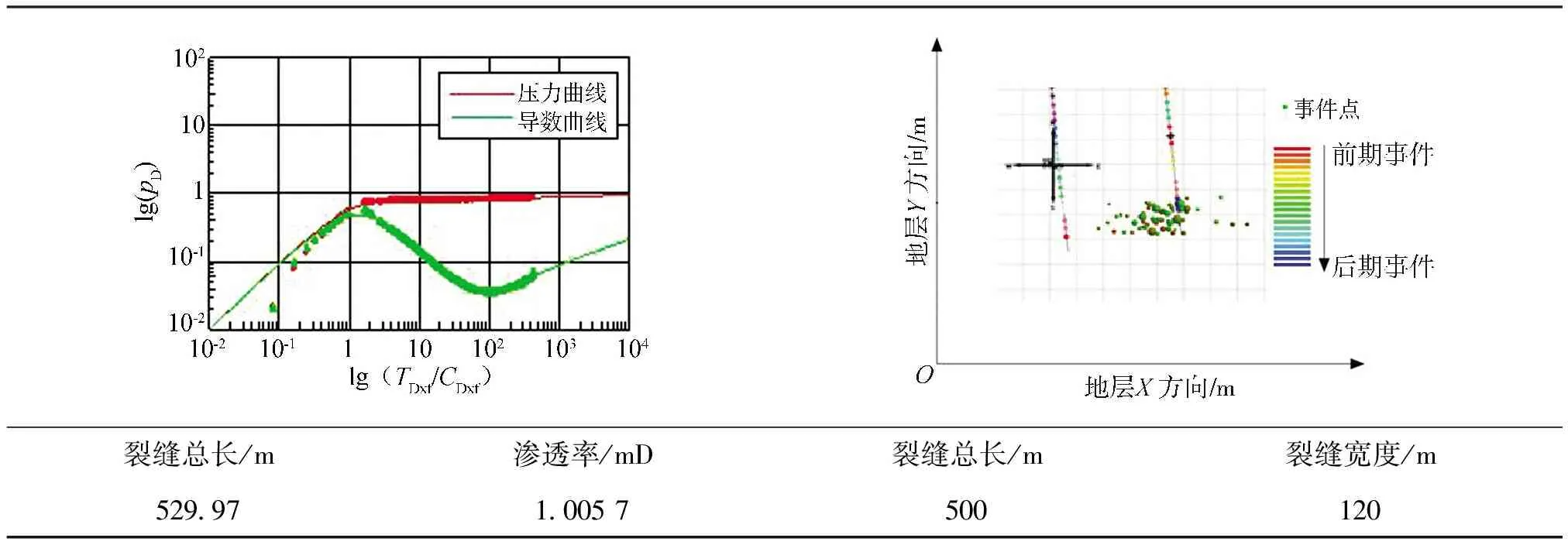
表1 第1段裂縫結果對比

表2 第5段裂縫結果對比

從表1和表2中可以看出，采用數字濾波壓裂停泵數據反演方法得到的曲線擬合結果非常好，第1段和第5段裂縫總長都很長，第5段裂縫區域的滲透率明顯比第1段裂縫區域的要高。與微地震結果相對比，可以看出裂縫總長比較接近，同時還可提供地層滲透率的擬合數據。對比結果表明，數字濾波壓裂停泵數據反演方法提供的裂縫參數較為準確。

通過上述方法，可以對總共19段裂縫分別進行數字濾波壓裂停泵數據反演。表3給出了19段裂縫解釋得到的裂縫半長及滲透率數據，可以看出裂縫半長第12段最短(74.9 m)，第1段最長(265 m)，滲透率第10段裂縫區域最大(18.81 mD)，第1段裂縫區域最小(1.01 mD)。這19條裂縫的平均裂縫半長為145.8 m。

依據這些數據與射孔位置數據，采用非均質地層多段壓裂水平井模型，根據本文提出的SRV區域反演方法，可以計算非均質地層中的地層壓力分布。通過對停泵數據的分析(圖3)，可以得到壓力傳播時間為5.5～6 h。根據表3給出的裂縫半長、滲透率數據，以及壓力傳播時間，結合公式(14)，最終得到示例井壓裂后的SRV區域示意圖。地層的網格劃分結果如圖5所示，最終繪制的SRV區域示意圖如圖6所示，圖6中黃色邊界線以內的區域即為SRV區域。

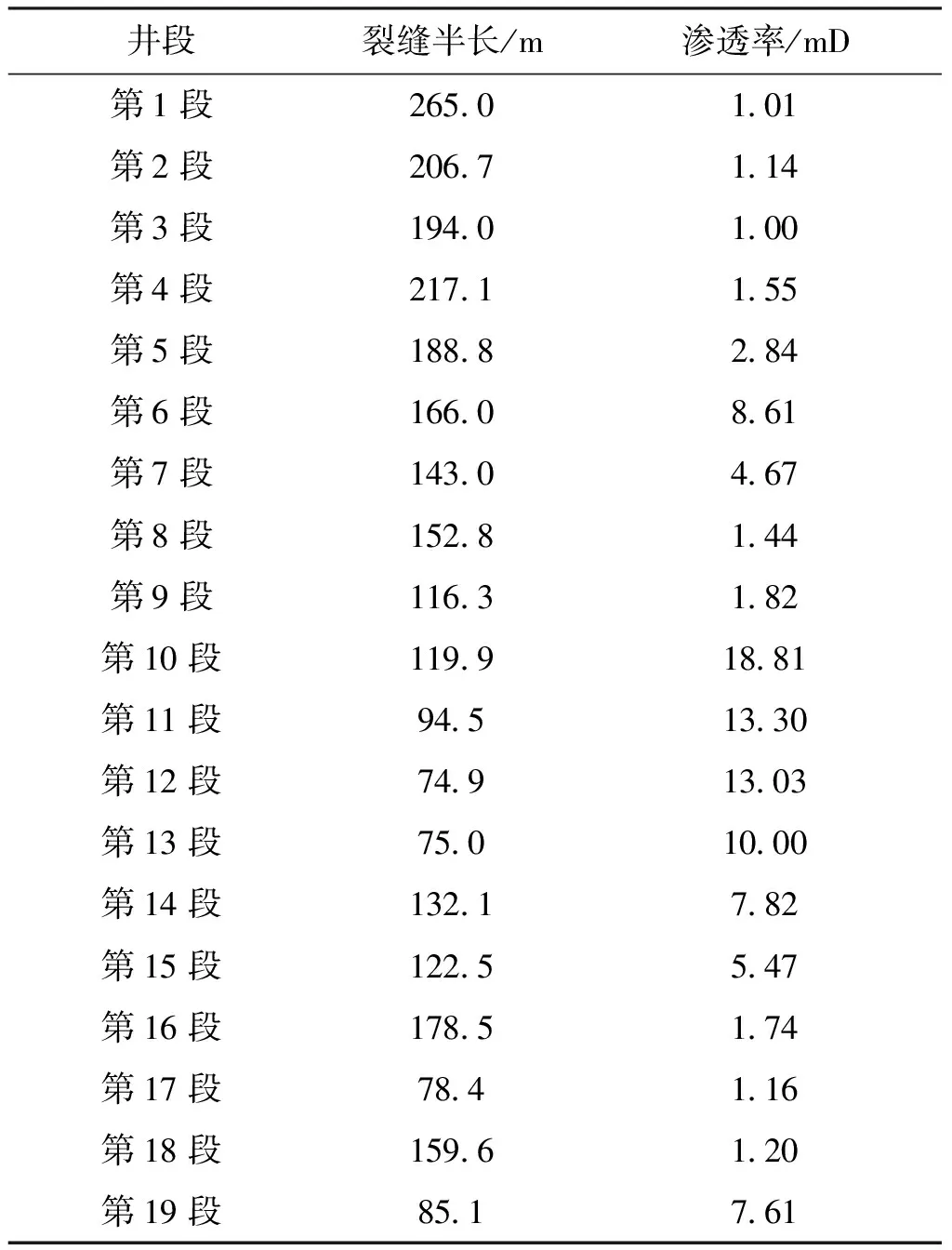
表3 示例井19段裂縫解釋結果

圖6 示例井SRV區域示意圖

通過對圖6進行分析整理，紅色區域為未改造的非SRV區域，也就是基質；黃色區域為低滲SRV區域，是SRV區域的最外圍；綠色區域為中滲SRV區域，此處存在大量微裂縫，因而滲透率較高；藍色區域為高滲SRV區域，主要由主裂縫及附近裂縫構成，此處滲透率非常高。從圖6中可以得到SRV區域主要集中在裂縫附近的結論，這與現場的實際情況較為符合。通過對SRV區域的分析，得到每條裂縫互相之間存在一定的干擾，整個地層的改造效果良好。對圖6進行統計計算，得到該示例井的SRV區域面積為545 884 m2。該井的壓裂效果比較理想，預估后續返排階段的排量會比較高。

為了驗證本文提出方法的正確性，根據圖6計算得到的SRV區域，調取示例井返排階段的壓力數據，如圖7所示。從圖7中可以看出，井底壓力前期較為平穩，呈慢速增長的趨勢。在20 h后，井底壓力開始勻速下掉，在40 h內下降了約2 MPa。

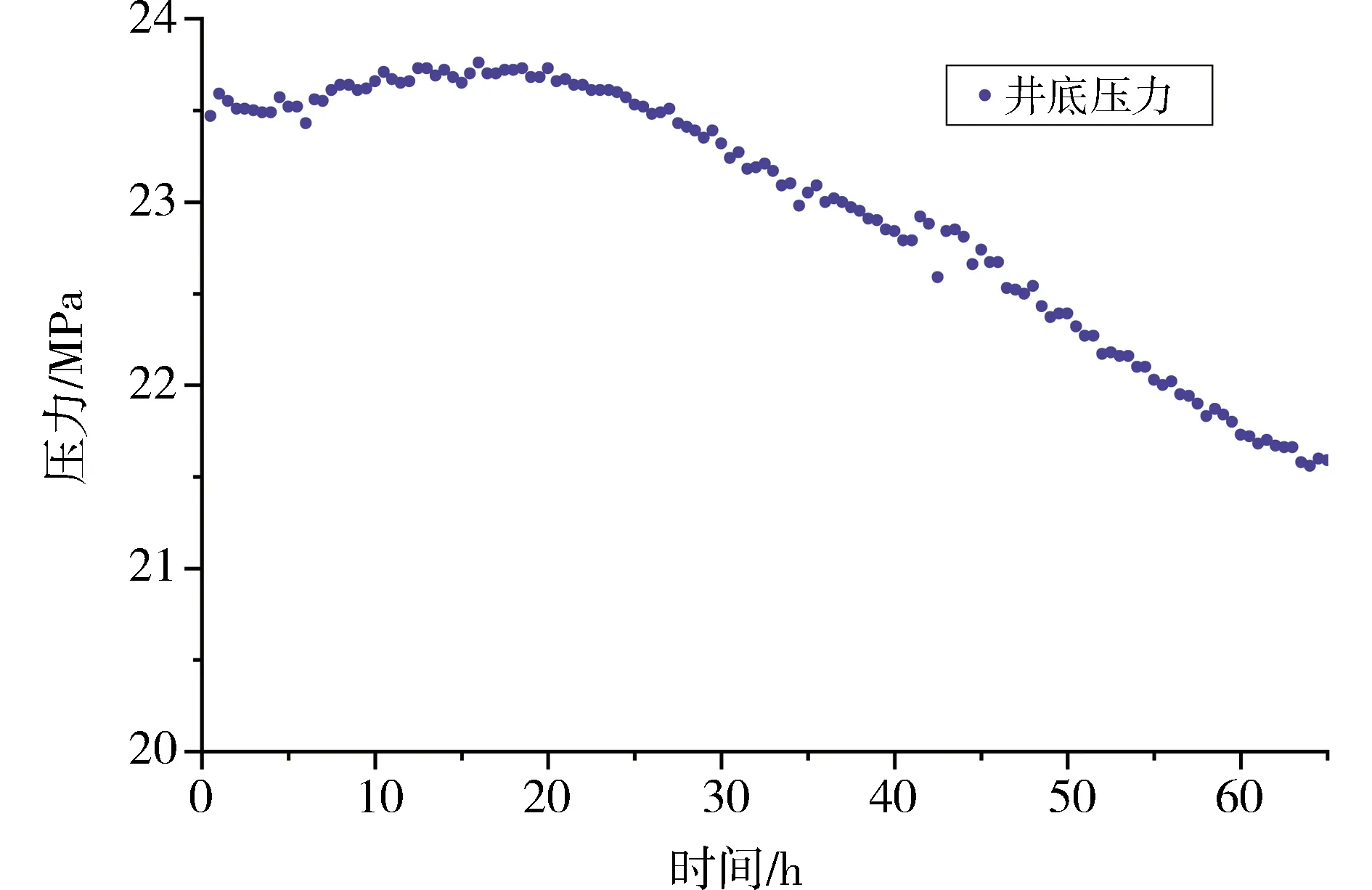
圖7 示例井返排階段實測壓力數據

根據圖7所示的壓力變化情況，模擬計算圖6所示的SRV區域產生的返排量數據，并與實測返排量數據進行對比，如圖8所示。可以看到，排量呈現下降先快后慢的趨勢，在前20 h排量從340 m3下降到240 m3，20 h后下降速度明顯減緩，但是出現了比較明顯的數據波動。此時，對應的壓力數據并無明顯震蕩。

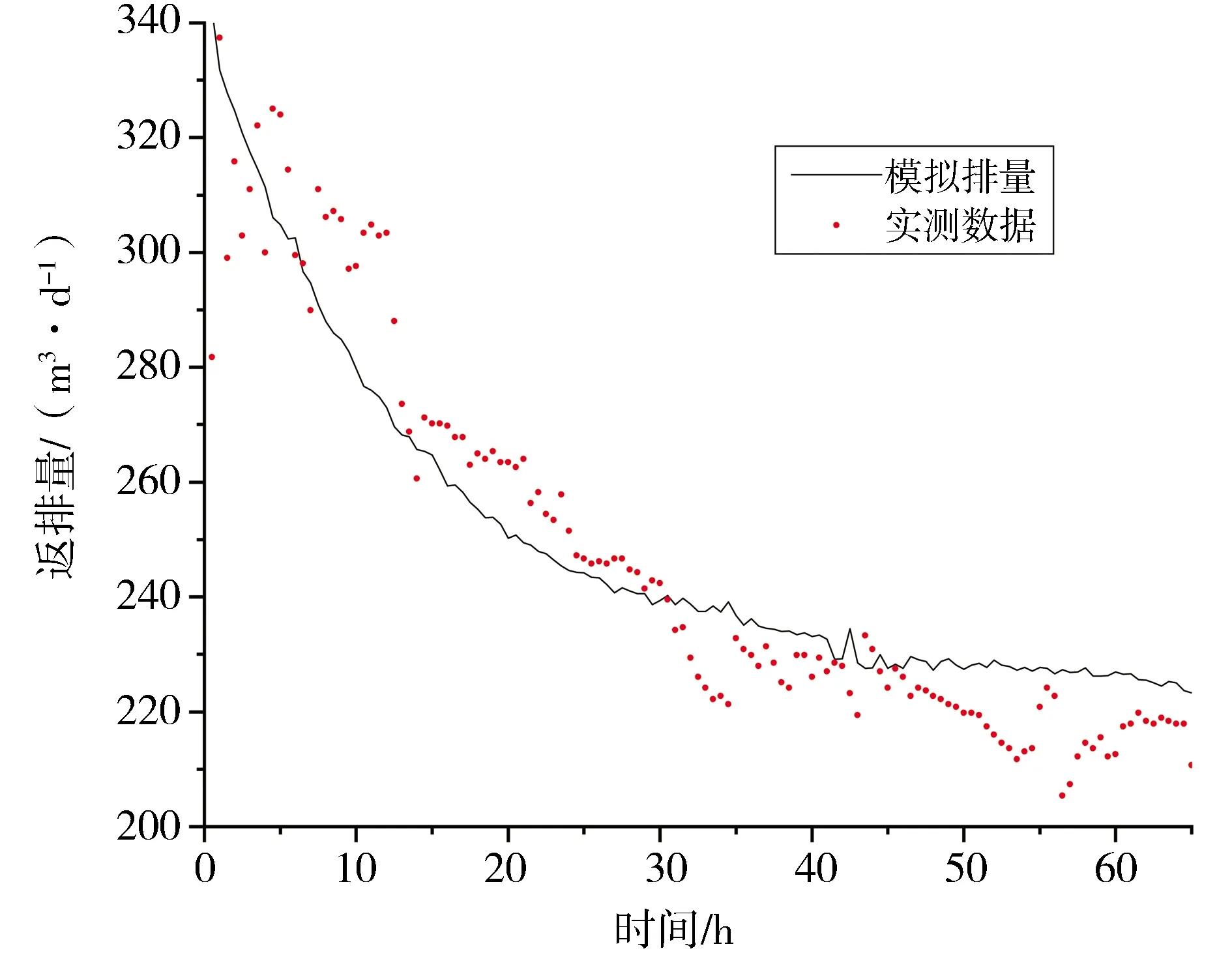
圖8 示例井返排階段實測流量數據與模擬排量對比

對圖8所示的返排量對比數據進行分析，可以看出前期的模擬效果較好(相對誤差在2%以內)，基本模擬出了整體排量的變化趨勢。后期擬合結果和實際排量有一定偏差(相對誤差在7%左右)。考慮到后期壓力變化比較均勻，排量變化不應該過于劇烈，特別是在55 h左右時，排量突然發生明顯變化，這應該是實際生產中產生的工程誤差。

經計算，整體實測數據和模擬排量之間的相對誤差在4.2%左右。可以看到，在工程誤差可以接受的范圍內，模擬結果與實測數據吻合得很好，證明了本文提出的SRV區域反演方法是正確可靠的，能夠為后續返排及生產提供合理的產能預測。

3 結論

本文基于壓力能夠波及的范圍即為SRV區域的設定，提出了通過計算地層壓力分布來反演SRV區域的新方法，不僅可以給出裂縫半長、SRV區域面積等壓裂評價參數，還可對后續返排和生產進行合理的產能預測。本文得到的主要結論如下：

(1)通過數字濾波壓裂停泵數據反演方法可以得到裂縫半長和地層滲透率，對停泵壓降曲線進行下降速度分析可以得到改造過程中的壓力傳播時間。

(2)通過上述關鍵參數，結合非均質性地層中多段壓裂水平井壓力分布的理論解，可以反演SRV區域，并通過裂縫局部加密方法，以圖形的方式描述裂縫和SRV區域的形態。

(3)選取國內某頁巖氣區塊的一口多段壓裂水平井停泵數據進行解釋反演，得到平均裂縫半長為145.8 m，SRV區域面積為545 884 m2。進行了返排期間的產能預測，與現場實測的返排數據對比，前期擬合效果很好(相對誤差在2%以內)，后期擬合效果稍差(相對誤差在7%左右)，整體相對誤差為4.2%，在可以接受的范圍內。結果證明了SRV區域反演方法的可靠性與正確性。

本文提出的SRV區域反演方法具有較強的時效性與通用性，為非常規油氣藏開發提供了高效的壓裂效果評價方法，相比目前常用的微地震監測方法大幅降低成本，具有重要的科學意義和廣闊的應用前景。