一類分?jǐn)?shù)階差分方程非局部邊值問(wèn)題解的存在唯一性 ①
吳 穎, 王良龍
(安徽大學(xué)數(shù)學(xué)科學(xué)學(xué)院,安徽 合肥 230601)
0 引 言
1965年, 著名數(shù)學(xué)家Leibniz和Hospital進(jìn)行了有意義的通信, 在通信中談及了分?jǐn)?shù)階導(dǎo)數(shù)以及分?jǐn)?shù)階微分[1]. 出于理論發(fā)展和應(yīng)用需要, 分?jǐn)?shù)階微分方程獲得極大發(fā)展, 其中Riemann-Liouville型分?jǐn)?shù)階微分方程更是引起了各界廣泛關(guān)注, 研究結(jié)果層出不窮[2,3].
眾所周知, 如同整數(shù)階微分方程, 對(duì)一般的分?jǐn)?shù)階微分方程也很難獲得其解的表達(dá)式或精確表示. 出于研究的需要, 當(dāng)把分?jǐn)?shù)階微分方程離散化時(shí)便得到相應(yīng)的分?jǐn)?shù)階差分方程.分?jǐn)?shù)階差分、分?jǐn)?shù)階和分以及分?jǐn)?shù)階差分方程理論的研究均具有很大的挑戰(zhàn)性, 所以吸引了許多中外學(xué)者的關(guān)注. 另一方面, 分?jǐn)?shù)階差分方程能很好地刻畫實(shí)際模型, 在材料科學(xué), 醫(yī)藥科學(xué), 生態(tài)數(shù)學(xué)模型上的研究中有著重要應(yīng)用[4-6].
目前很多學(xué)者在分?jǐn)?shù)階差分方程方向做出了的一些結(jié)果,其中絕大部分研究了階數(shù)在1-2之間的分?jǐn)?shù)階差分方程,還有一小部分攻克了階數(shù)在3-4之間的分?jǐn)?shù)階差分方程,在合適的條件下均獲得了不錯(cuò)的結(jié)果[7,8].本文在前人的基礎(chǔ)上考慮了一類任意階的分?jǐn)?shù)階差分方程的非局部邊值問(wèn)題,運(yùn)用了Banach不動(dòng)點(diǎn)定理, Brouwer不動(dòng)點(diǎn)定理在合適的條件下得出該分?jǐn)?shù)階差分方程非局部邊值問(wèn)題解的存在唯一性.
1 預(yù)備知識(shí)
本節(jié)給出若干記號(hào), 定義和預(yù)備引理[6,8].
函數(shù)y(t)的一階差分記為Δy(t)=y(t+1)-y(t). 設(shè)N,b是非負(fù)整數(shù),v∈R, 記
Nv={v,v+1,…},
Nv-N,v+b={v-N,v-N+1,…,v+b}.
考慮如下一般形式分?jǐn)?shù)階差分方程的非局部邊值問(wèn)題
(1)
其中N-1 定義1.2若v>0, 函數(shù)y(t)的v-階和分定義為 函數(shù)y(t)的v-差分定義為 Δvy(t)=ΔNΔ-(N-v)y(t),t∈Nv-N,v+b, 其中N是非負(fù)整數(shù), 滿足N-1 引理1.1令0 其中ci∈R, 1iN. 引理1.3分?jǐn)?shù)階差分、分?jǐn)?shù)階和分運(yùn)算具有下列性質(zhì): (1)令u>0,v>0, 有Δ-vΔ-uy(t)=Δ-(u+v)y(t). (2)令N是滿足N-1 引理1.4記Y={y:Nv-N,v+b→R},f:Nv-N,v+b×R→R是連續(xù)函數(shù),g:Y→R是一個(gè)連續(xù)泛函, 則函數(shù)y(t)是分?jǐn)?shù)階差分方程非局部邊值問(wèn)題(1)的解, 當(dāng)且僅當(dāng)y(t)滿足 (2) 其中t∈Nv-N,v+b,N是滿足N-1 證明:充分性: 由引理1.1可得 (3) 且 由(1)知 y(v+b)=-Δ-vf(t,y(t))|t=v+b+ (4) 由上式(4)解得 所以 充分性得證. 必要性顯然成立就不在此贅述了, 綜上, 引理1.4得證. Y如前所定義, 對(duì)任意的y∈Y, 定義‖y‖=max{|y(t)|:t∈Nv-N,v+b}, 則(Y,‖·‖)是一個(gè)Banach空間,定義算子T:Y→Y, 其中 (5) 定理2.1假設(shè)f(t,y)和g(y)對(duì)y滿足Lipschitz條件, 即存在α>0,β>0使得 |f(t,z1)-f(t,z2)|α|z1-z2|, t∈Nv-N,v+b,z1,z2∈R, |g(y1)-g(y2)|β‖y1-y2‖,y1,y2∈Y, 若 (6) 則非局部邊值問(wèn)題(1)存在唯一解. 證明:只要證明T:Y→Y是一個(gè)壓縮映射, 對(duì)任意給定的y1,y2 ‖Ty1-Ty2‖α‖y1-y2‖× (7) 由引理1.2知 (8) 且 α‖y1-y2‖× (9) 由引理1.2(5)得 (10) 綜上得 ‖Ty1-Ty2‖ 則T:Y→Y是一個(gè)壓縮映射, 由Banach壓縮映射原理知邊值問(wèn)題(1)的解存在唯一. 定理2.2假設(shè)存在常數(shù)M>0使得f(t,z)和g(y)滿足下列條件 證:令Y0={y∈Y:‖y‖M},則Y0是Y的有界凸閉集. 記 則ω0是嚴(yán)格正常數(shù),由定理2.1知 ‖Ty‖+ 因此,T:β→β, 又f(t,y(t)),g(y)均連續(xù), 易知T為連續(xù)算子, 由Brouwer不動(dòng)點(diǎn)定理存在T, 使得Ty0=y0,y0∈β,y0是邊值問(wèn)題(1)的解,y0滿足|y0(t)|M. 利用壓縮映射原理和Brouwer不動(dòng)點(diǎn)定理在合適的條件下討論了一類階數(shù)任意的分?jǐn)?shù)階差分方程非局部邊值問(wèn)題解的唯一性與存在性,實(shí)際上還可以繼續(xù)研究該問(wèn)題的正解的存在性.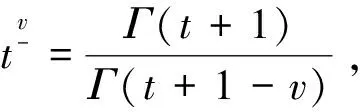
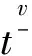
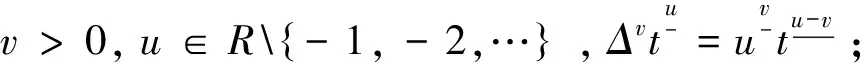


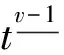
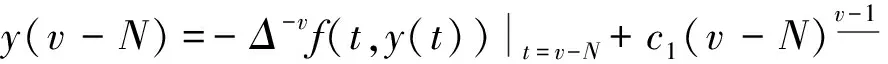


2 解的存在唯一性
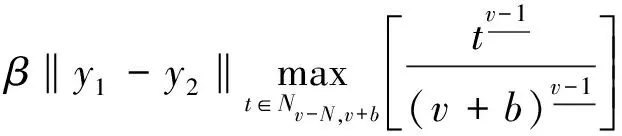
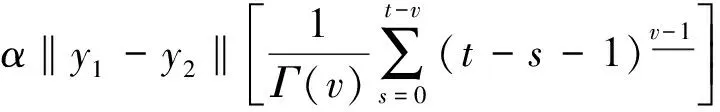

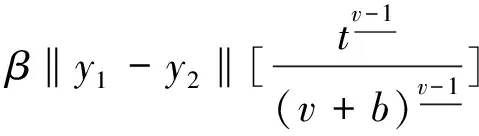
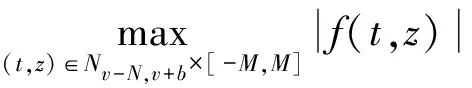
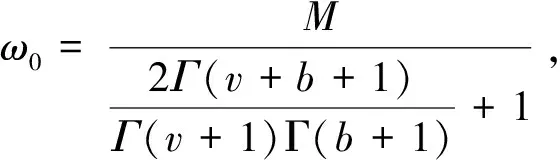

3 結(jié) 語(yǔ)

