合成信息系統與有限個子系統的屬性特征研究 ①

方連花， 林玉梅， 李克典

(1.泉州信息工程學院2.通識教育中心，福建 泉州 362000,3.閩南師范大學數統學院,福建 漳州 363000)

0 引 言

粗糙集理論[1]是繼概率論、模糊集、證據理論之后的又一個刻畫不完整性和不確定性的數學工具。目前，許多學者從各個方面對目標信息系統的知識獲取和規則提取做了深入的研究，并且取得了大量成果[2-8]。一個信息系統的知識庫往往都是確定的，但在實際應用中，經常會在原信息系統上添加有限個研究對象，或者增加(刪除)屬性特征，進而對新信息系統進行分類、知識獲取等等。在這方面，已經有學者對其進行了研究，文獻[9]在等價關系的前提下研究了合成信息系統與子信息系統的屬性約簡問題。由于現實中有些信息是不確定、不完備或者是多值的系統，文獻[10]在優勢關系下研究序信息系統的合成與分解的屬性特征，文獻[11]和[12]分別在擬序關系下研究合成集值信息系統以及決策表的屬性特征。他們的研究主要是基于兩個信息系統的合成，而在實際問題中并不僅僅只有兩個子系統的合成與分解，信息系統中又會存在大量的冗余數據，因此研究有限多個信息系統的合成以及其屬性特征是有必要的。給出任意有限個對象合成信息系統和有限個屬性合成信息系統的概念，分別討論了它們的屬性特征與有限個原子信息系統的屬性特征之間的關系。

1 對象合成信息系統

定義1.1[5]I=(U,A,F)是一個信息系統，其中

U是對象集，U={x1,x2,…,xn}；A是條件屬性集，A={a1,a2,…,ap}；

F是U與A的關系集，F={fk:U→Vk,k≤p}，Vk是ak的有限值域。

信息系統中的不同屬性對劃分有不同的作用，有的屬性是必不可少的，稱為核心屬性；有的屬性是可以被其他屬性代替的，稱為相對必要屬性；有的屬性是根本不需要的，稱為不必要屬性。下面給出這三種屬性特征的數學刻畫。

定義1.3[13]設I=(U,A,F)是一個信息系統，對于B?A，若RB=RA,稱B是劃分協調集。若B是劃分協調集，而B的任何真子集均不是劃分協調集，則稱B是劃分約簡集。

定義1.4[13]設I=(U,A,F)是一個信息系統，Bk(k≤r)為所有劃分約簡集，

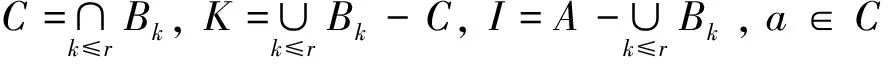
在信息系統中，為了研究不同屬性的特征，在文獻[14]和[15]中有如下等價刻畫定理：

定理1.1[14]設(U,A,F)是信息系統，則有以下結論：

(1)a是劃分核心當且僅當RA-{a}≠RA；

(2)a是劃分不必要屬性當且僅當R(a)?Ra，其中R(a)=∪{RB-{a}|RB?RA,B?A}；

(3)a是劃分相對必要屬性當且僅當RA-{a}=RA成立且R(a)?Ra不成立。

定理1.2[15]設(U,A,F)是信息系統，則有以下結論：

(1)a是劃分核心當且僅當RA-{a}?Ra不成立。

(2)a是劃分不必要屬性或者劃分相對必要屬性當且僅當RA-{a}?Ra成立。

根據定義1.3、定義1.4和定理1.1、定理1.2可以得到對象合成信息系統的協調集、不必要屬性、相對必要屬性與n個原子信息系統的屬性特征之間的關系。

定理1.3設(∪Ui,A,∪Fi)為信息系統(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的對象合成信息系統，B?A。若B是(∪Ui,A,∪Fi)的一個約簡，則B分別是(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的協調集。

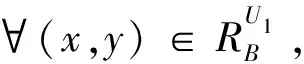
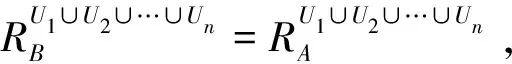
同理可證，B分別是(U2,A,F2)，…，(Un,A,Fn)的協調集。

定理1.4設(∪Ui,A,∪Fi)為信息系統(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的對象合成信息系統，a∈A。若a是(∪Ui,A,∪Fi)的不必要屬性，則a分別是(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的不必要屬性。

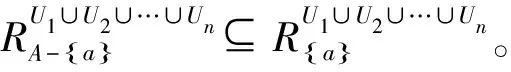
同理可證，a分別是(U2,A,F2)，……，(Un,A,Fn)的不必要屬性。

定理1.5設(∪Ui,A,∪Fi)為信息系統(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的對象合成信息系統，則(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的核心屬性一定是(∪Ui,A,∪Fi)的核心屬性。

同理可證，(U2,A,F2)，…，(Un,A,Fn)的核心屬性是(∪Ui,A,∪Fi)的核心屬性。

例1.1通過例子驗證定理1.3、定理1.4和定理1.5的結論。

設(U1,A,F1),(U2,A,F2),(U3,A,F3)是三個信息系統，表1是它們的對象合成信息系統(U1∪U2∪U3,A,F1∪F2∪F3)，其中A={a,b,c}，U1={x1,x2,x3}，U2={x4,x5,x6,x7}，

U3={x8,x9,x10,x11,x12}。

由劃分的定義可得對象合成信息系統(U1∪U2∪U3,A,F1∪F2∪F3)的等價類為{x1,x9,x11}，{x2,x3,x8}，{x4,x6}，{x5,x7,x10}，{x12}。

根據辨識矩陣，容易得出{a,c}是(U1∪U2∪U3,A,F1∪F2∪F3)的一個約簡，則由定理1.3知，{a,c}分別是(U1,A,F1),(U2,A,F2)和(U3,A,F3)的協調集；容易驗證{b}是(U1∪U2∪U3,A,F1∪F2∪F3)的不必要屬性，則由定理1.4知，{b}分別是(U1,A,F1),(U2,A,F2)和(U3,A,F3)的不必要屬性；容易驗證{c}是(U1,A,F1)的核心屬性，由定理1.5知{c}是(U1,A,F1),(U2,A,F2),(U3,A,F3)的核心屬性。

2 屬性合成信息系統

Ai∩Aj=?,i≠j。

定 理2.1設(U,∪Ai,∪Fi)為系統(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的屬性合成系統，對于任意的Bi?Ai，若Bi是(U,Ai,Fi)的一個約簡，則∪Bi是(U,∪Ai,∪Fi)的協調集。

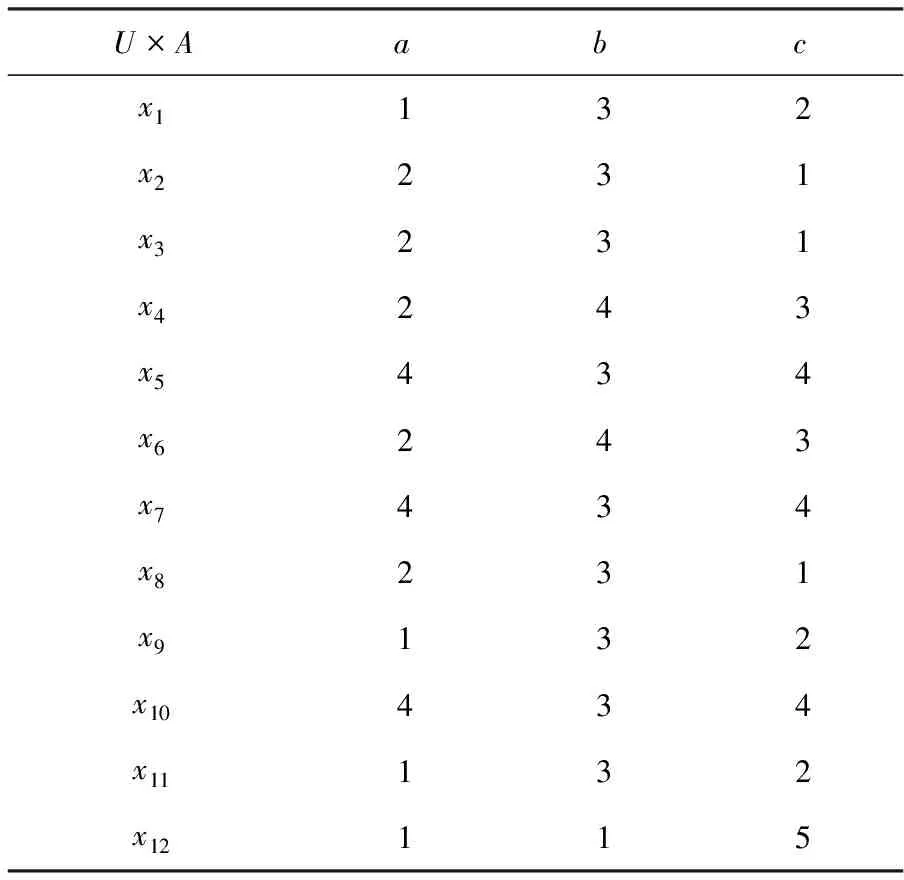
表1 對象合成信息系統

證 明：設?(x,y)∈RB1∪B2∪…∪Bn，若RB1∪B2∪…∪Bn=∩RBi則(x,y)∈∩RBi。若∩RBi=∩RAi=RA1∪A2∪…∪An則(x,y)∈RA1∪A2∪…∪An，即RB1∪B2∪…∪Bn?RA1∪A2∪…∪An。另一方面，RA1∪A2∪…∪An?RB1∪B2∪…∪Bn。因此，RA1∪A2∪…∪An=RB1∪B2∪…∪Bn，即∪Bi是(U,∪Ai,∪Fi)的協調集。

定理2.2設(U,∪Ai,∪Fi)為信息系統(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的屬性合成信息系統，則(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的不必要屬性一定是(U,∪Ai,∪Fi)的不必要屬性。

證 明：設a∈A1是(U,A1,F1)的不必要屬性，則由定理1.2可知RA1-{a}?R{a}。若RA1∪A2∪…∪An-{a}?RA1-{a}，則RA1∪A2∪…∪An-{a}?R{a}，所以a是(U,∪Ai,∪Fi)的不必要屬性。

同理，(U,A2,F2)，…，(U,An,Fn)的不必要屬性一定是(U,∪Ai,∪Fi)的不必要屬性。

定理2.3設(U,∪Ai,∪Fi)為信息系統(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的屬性合成信息系統，a∈∪Ai。若a是(U,∪Ai,∪Fi)的核心屬性，則當a∈Ai時，a是(U,Ai,Fi)的核心屬性。

證 明：設a∈Ai是(U,∪Ai,∪Fi)的核心屬性，則由定理1.2可知RA1∪A2∪…∪An-{a}?R{a}，即?x,y∈U，滿足(x,y)∈RA1∪A2∪…∪An-{a},(x,y)?R{a}。又因為RA1∪A2∪…∪An-{a}?RAi-{a}，故(x,y)∈RAi-{a}，即RAi-{a}?R{a}。因此，a是(U,Ai,Fi)的核心屬性。

3 結 語

目前關于知識系統合成的研究都是基于兩個信息系統的合成，而在實際問題中并不僅僅只有兩個子系統的合成與分解，信息系統中又會存在大量的冗余數據，因此研究有限多個信息系統的合成以及其屬性特征是有必要的。文中給出了任意有限個對象合成信息系統和有限個屬性合成信息系統的概念，分別討論了它們的核心屬性、不必要屬性、相對必要屬性等屬性特征與有限個原子信息系統的屬性特征之間的關系。并通過實例驗證了該方法的有效性，為今后進一步研究合成信息系統與有限個子信息系統的屬性約簡問題奠定了基礎。