車載綜合電力系統大信號失穩預測

高 強，袁 東，劉春光，魏曙光

(陸軍裝甲兵學院 兵器與控制系， 北京 100072)

新型輪式電傳動裝甲車電力系統是由分布式電源、變換器和負載組成的小型發配電系統，稱為車載綜合電力系統[1-2]。與以往大電網、小型輸配電站以及艦載電力系統不同，車載綜合電力系統只能工作于離網(孤島)模式，且負載、變流器數量種類多，系統非線性強，表現為“弱慣性”系統[3-4]。

系統負載尤其是電機等屬于恒功率負載(Constant power load,CPL)，其“負阻抗”特性可使系統受到干擾時逐漸遠離穩態工作點，導致系統瀕臨崩潰[5]；再者變流器的控制參數如果選取不當會導致母線電壓低頻振蕩、電源噪聲大、能量轉換效率低等問題；車輛啟動、剎車、加/減速模式快速切換，對電力系統表現為瞬間突加/卸負載，如不能快速響應勢必造成母線電壓失穩，從而使車內精密設備無法正常運行[6-8]。然而電機功率突變多少、變換器參數取值如何才會導致系統失穩仍然未知。因此，進行此類電力系統的穩定邊界研究至關重要。

文獻[9-10]基于系統的小信號線性模型，分別采用等效環路增益法、阻抗禁止區法等進行系統分析，從理論上分析了部分參數對系統穩定性的影響。文獻[11]使用Lyapunuov間接法，通過判斷系統矩陣的特征值是否在單位圓內來評價系統的穩定性，給出了系統穩定條件。以上方法都在一定程度上保證了系統的穩定運行，取得良好效果。但對于車載綜合電力系統來說，存在輸入電壓波動或者大功率負載投切等大信號擾動，傳統的基于穩態工作點的小信號穩定性分析已不能保證系統的穩定性，為此需進行大信號穩定性分析。大信號穩定分析也是基于某一平衡狀態，但旨在確定該平衡狀態的吸引域大小，確定系統在大信號擾動下的失穩邊界。

本文以某型8*8輪式裝甲車車載綜合電力系統為基礎，建立了靜音行駛模式下系統的大信號模型，利用混合式函數理論推導了系統穩定域。據此探究了DC/DC變換器電壓外環控制器比例系數、電機負載突變功率對系統穩定域的影響規律，最后通過硬件在環仿真實驗驗證了該穩定域對系統失穩預測的正確性。

1 車載綜合電力系統建模

某型8*8輪式電傳動裝甲車車載綜合電力系統拓撲結構如圖1所示，本文主要研究該車在靜音行駛模式下系統失穩預測問題。在靜音行駛時發動機—發電機組停止工作，系統由動力電池供電，負載主要為8個輪轂電機，拓撲結構如圖1中虛線框內所示。

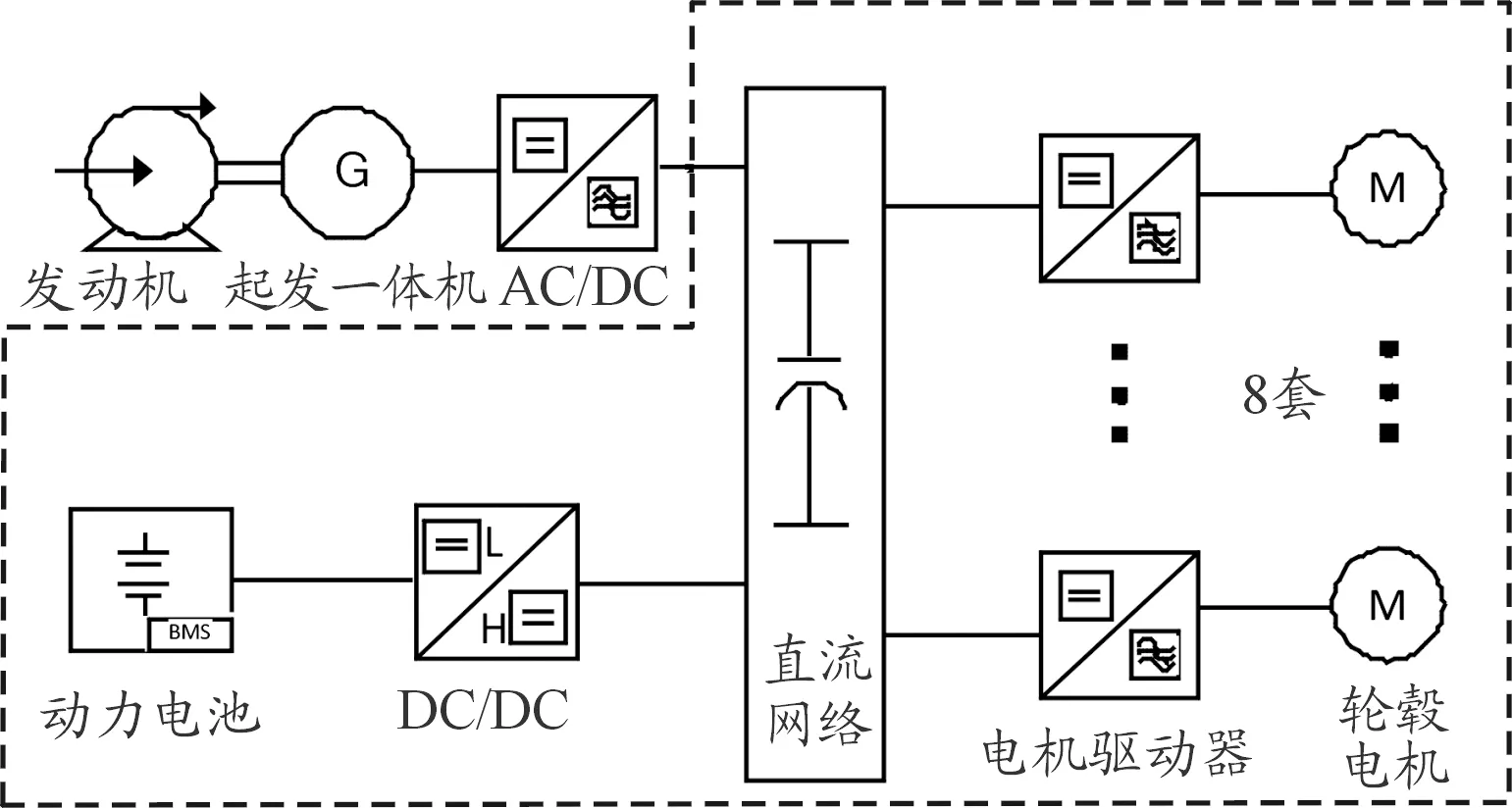
圖1 靜音行駛時車載電力系統拓撲結構

根據靜音模式下系統拓撲結構，為方便后文分析，首先對DC/DC變換器、電機負載進行建模，從而建立系統的大信號模型。

1.1 DC/DC變換器大信號建模

由于存在IGBT高頻通斷使得DC/DC變換器呈現非線性，不便于分析。因此可將變換器視為輸入/輸出的二端口網絡，根據功率守恒原理，利用回轉器進行替代從而達到簡化模型的目的，由此得到基于回轉器的DC/DC變換器大信號模型[12]如圖2所示。

圖2 DC/DC變換器大信號模型示意圖

其中Ubat、Udc分別為電池電壓與母線電壓開關周期平均值，Ibat、Iout分別為電池電流與變換器輸出電流開關周期平均值，Iload為穩態負載電流，Uref為電壓反饋網絡的參考電壓，C為支撐電容，反饋網絡與原變換器相同。

g為可調回轉電導，由反饋網絡的控制變量u和常數k的乘積組成，用于調節控制環飽和時變換器中的被控電流所能達到的最大值。由于回轉器具有電壓電流對偶轉換的特性，則僅采用單環反饋配合回轉器特性即實現電壓、電流雙環反饋的功能。

根據回轉器特性有：

(1)

車輛行駛過程中DC/DC處于Boost工作模式，此時電路拓撲結構如圖3所示。

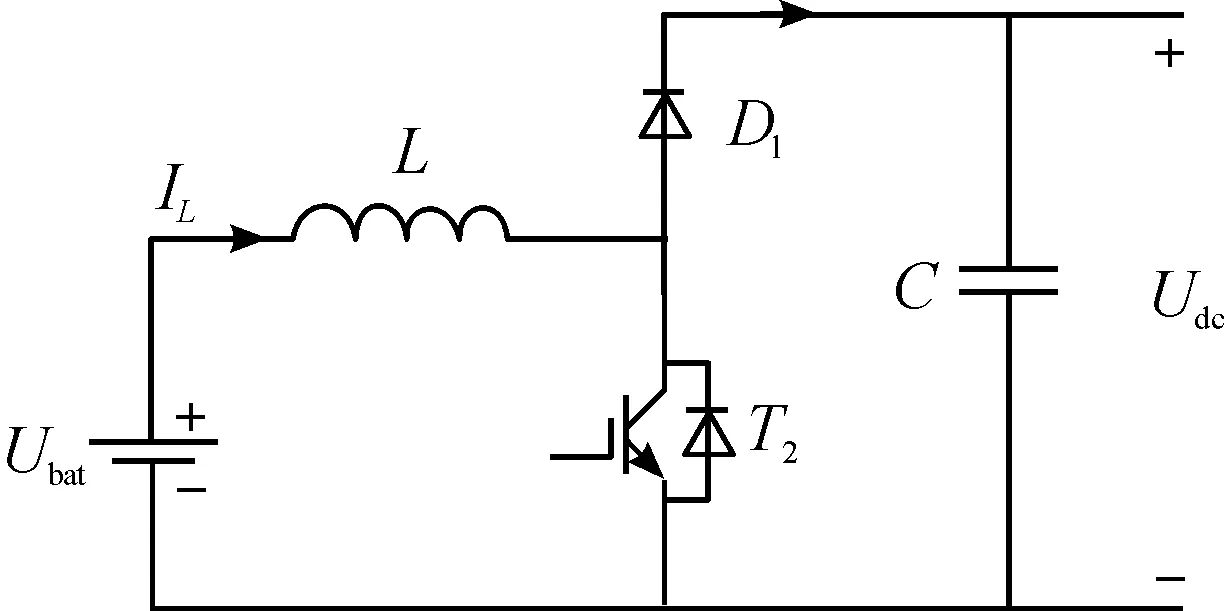
圖3 DC/DC變換器Boost工作模式

該模式下，電池向母線供電，按上圖定義流入電感電流為正方向，此時電感電流IL即為大信號模型的輸入電流Iin，則

IL=Iin=Udc·g

(2)

又因g=u·k

其中，u為電壓環的輸出，即電流參考值Iref；系統穩態后有

Iin=Iref=u

(3)

因此

(4)

1.2 電機負載的大信號模型

輪轂電機驅動器采用閉環控制，且閉環響應速度遠大于源變流器，因此可將電機控制器-輪轂電機負載等效為恒功率負載[13]。為了分析方便，認為車輛行駛過程中載荷平均，即8個電機狀態一致。則電機負載大信號模型可以簡化為圖4。

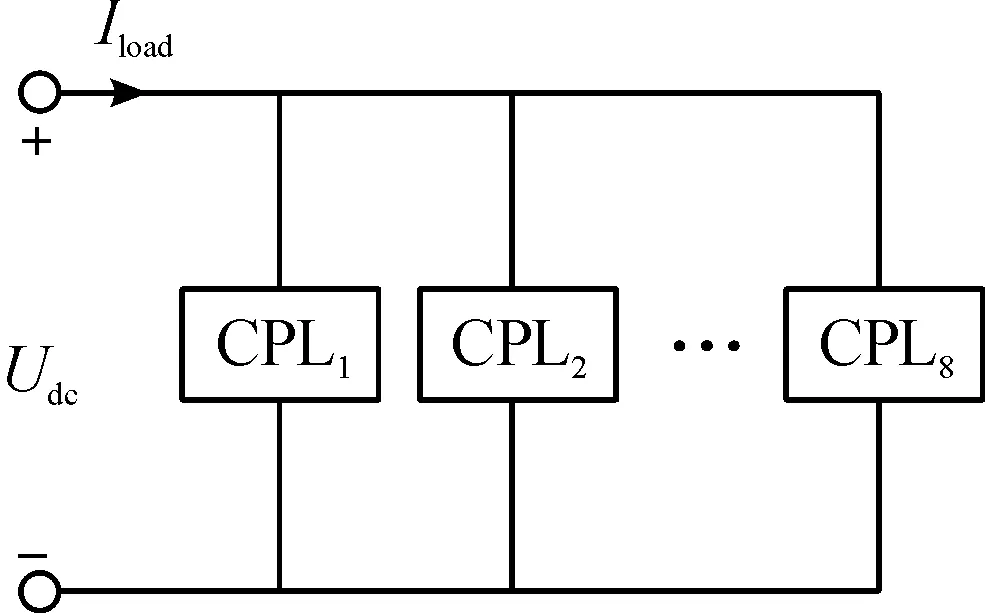
圖4 電機負載大信號模型

則負載總功率為

Pload=Iload·Udc=a(常數)

(5)

2 車載綜合電力系統穩定域估計

2.1 基于混合勢函數理論的系統穩定域估計

混合勢函數理論主要用來分析非線性電力系統穩定性，通過建立系統能量函數，根據混合勢理論的相關定理可判定系統能否穩定運行[14]。混合勢函數形式為

P(i,v)=-A(i)+B(v)+iT·(γv-α)

(6)

式中:A(i)為電流勢函數；B(v)為電壓勢函數；i為電感電流向量；v為電容電壓向量；γ為常數矩陣；α為常向量。

根據回轉器原理可將系統的大信號模型進一步簡化為圖5所示。

圖5 簡化的大信號模型

其中

(7)

可得系統中非儲能元件電流勢函數為：

(8)

超級電容支路電壓電乘積為

(9)

則可得系統的混合勢函數為：

(10)

對比式(6)與式(10)可得

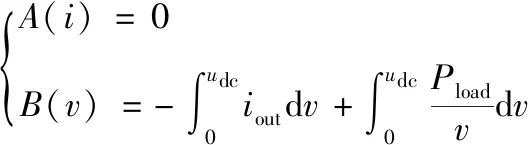
(11)

則

(12)

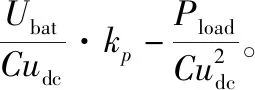
根據混合勢函數理論第三條穩定性定理[15]，系統必須滿足μ1+μ2>0，則系統的解將趨近于穩態工作點，因此可得系統的穩定域為

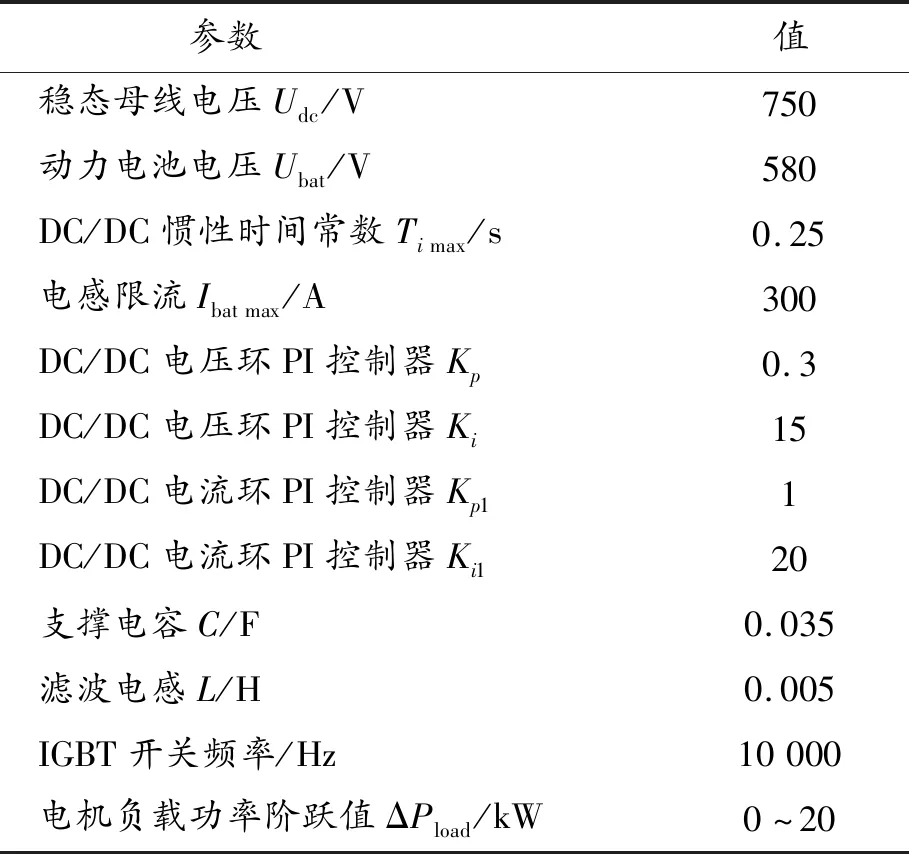
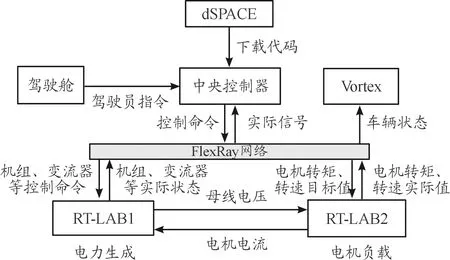
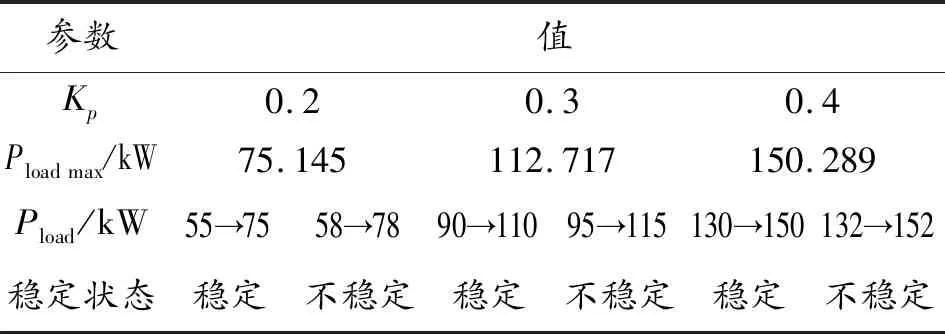
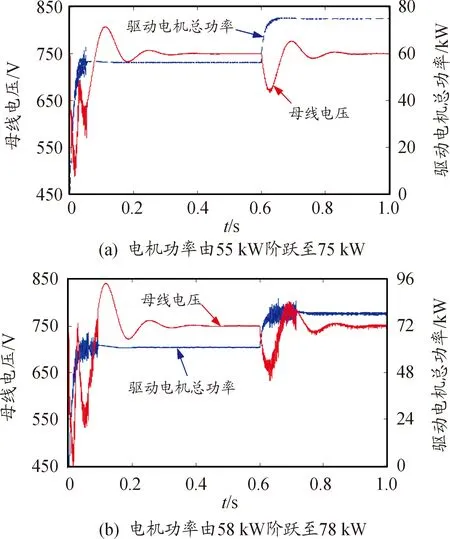
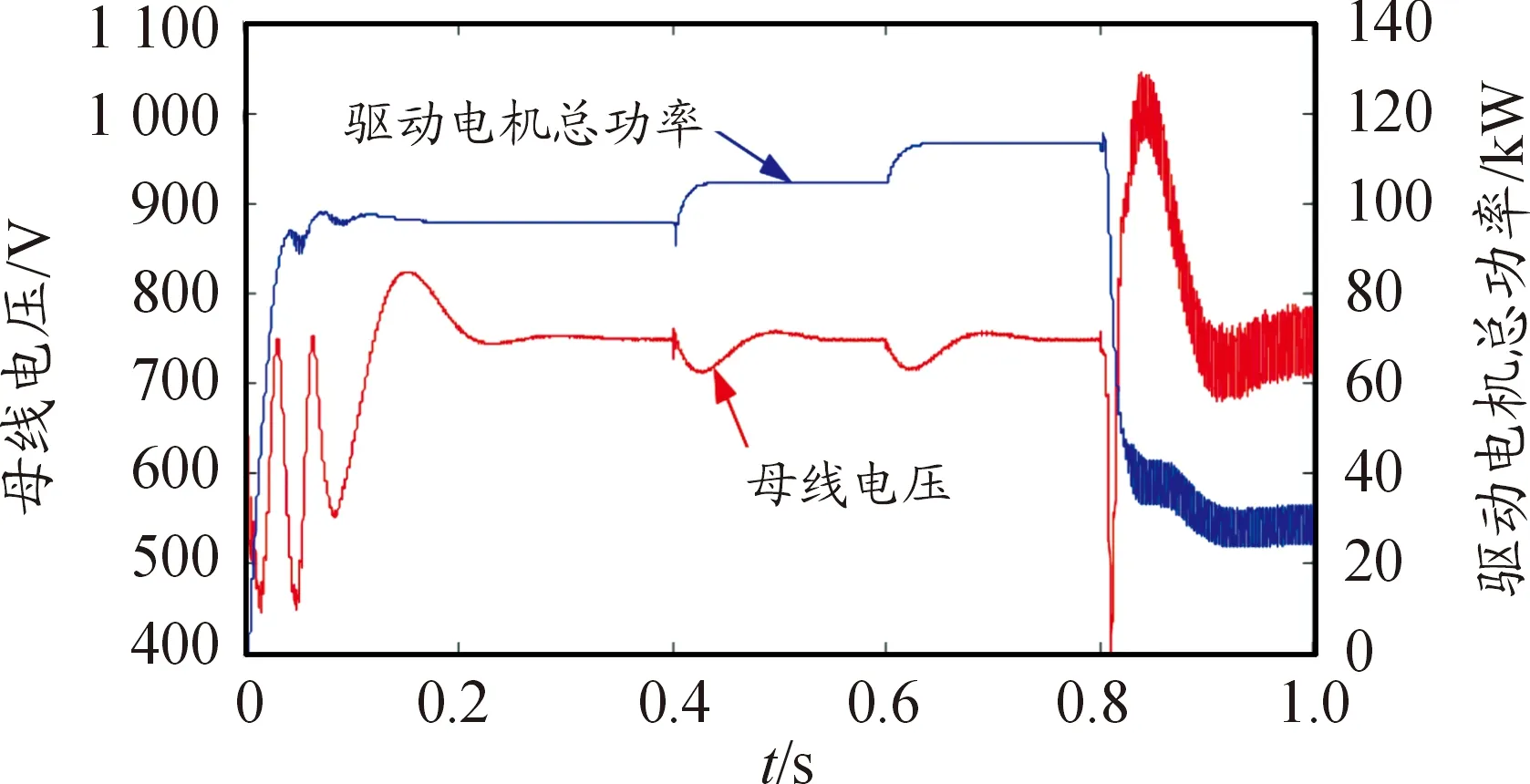
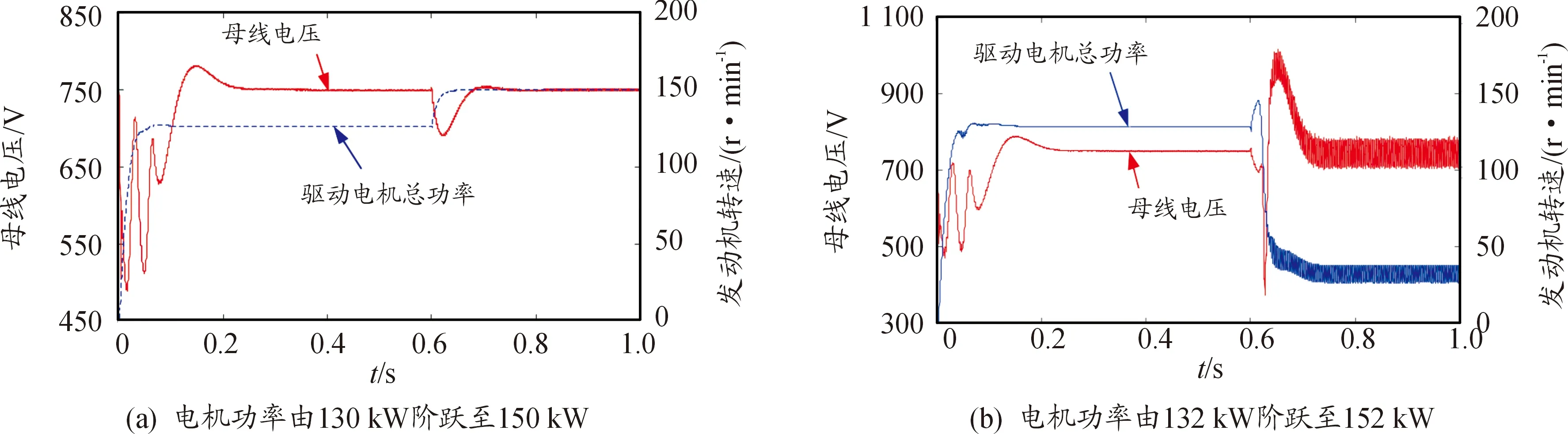
Pload

(13)

式中udc為暫態母線電壓，要將瞬時母線電壓可能的最小值Udcmin考慮在內，因此需要對上式結果進行修正。

假設負載功率瞬間突增，其能量全部由支撐電容補充，則有

(14)

其中Timax為DC/DC變換器響應慣性時間常數。

則可得修正后的系統穩定域為：

(15)

2.2 系統穩定域估計

以上方法求解系統穩定域只針對系統拓撲結構進行分析，并未考慮源的輸出能力有限性，而為了保護電源，實際情況下往往會對變換器電感電流作限流處理，設該系統電感電流最大值為Ibat max。則根據功率守恒易得

Pload

(16)

則結合式與式可得最終估計的系統穩定域為

(17)

給出該車載綜合電力系統部分電器參數如表1所示。

表1 車載綜合電力系統部分電氣參數

結合系統電氣參數以及式(17)，分析有：

3 硬件在環仿真實驗

為了驗證所推導系統穩定域的合理性，開展了硬件在環仿真實驗。利用dSPACE生成控制器代碼并下載到中央控制器；Vortex搭建車輛動力學模型模擬實車場景；RT-LAB1模擬車載電力系統、RT-LAB2模擬驅動電機系統；各模塊之間建立FlexRay網絡構成硬件在環仿真環境，結構如圖6所示。

圖6 硬件在環仿真系統結構框圖

首先，驗證DC/DC電壓環PI控制器比例系數Kp小于0.4時增加Kp值對系統穩定域的影響。令ΔPload為20 kW，根據式(17)計算出理論上電機功率最大值以及電機功率階躍時系統的穩定狀態預測如表2所示。

表2 Kp對系統穩定域的影響預測

圖7為Kp取0.2負載功率階躍時母線電壓與負載功率波形，圖7(a)中驅動電機功率在0.6 s時從55 kW階躍至75 kW，母線電壓經過衰減震蕩后保持穩定；圖7(b)中驅動電機功率在0.6 s時從58 kW階躍至78 kW，母線電壓出現較大波動，且雖然在0.9 s左右恢復到750 V但波形具有大量諧波，系統穩定性變差，仿真結果與理論預測的系統穩定狀態基本一致。

圖7 Kp為0.2，負載功率階躍時系統仿真波形

圖8為Kp取0.3電機功率階躍時系統仿真結果。圖8(a) 中驅動電機功率在0.6 s時從90 kW階躍至110 kW，母線電壓保持穩定；圖8(b)中驅動電機功率由95 kW階躍至115 kW，母線電壓出現約±50 V的震蕩，負載功率亦無法達到115 kW，系統崩潰。仿真結果與穩定域預測結果一致。

圖8 Kp為0.3，負載功率階躍時系統仿真波形

為驗證電機負載功率階躍值ΔPload對系統穩定性的影響，在Kp為0.3時，根據式(17)計算出理論上電機功率最大值以及電機功率階躍時系統的穩定狀態預測如表3所示。

表3 對系統穩定狀態預測

圖9為Kp取0.3，ΔPload取10 kW，電機功率階躍時系統仿真波形。通過對比圖9與圖8(b)發現，系統參數除ΔPload以外其他一致。圖8(b)中電機功率由95 kW直接階躍至115 kW，母線電壓失穩，系統崩潰；而圖9中，電機功率在 0.4 s 由95階躍至105 kW，然后在0.6 s時階躍至115 kW，母線電壓波動后恢復750 V，系統保持穩定，說明減小ΔPload有效提高了系統帶載能力；在0.8 s階躍至125 kW時母線電壓失穩，系統崩潰。仿真結果與表3中通過式(17)理論預測得到的結果一致。

圖9 Kp取0.3，ΔPload取10 kW電機功率階躍時仿真波形

圖10為Kp取0.4電機總功率階躍時系統的仿真波形。圖10(a)中電機功率在0.6 s由130 kW階躍至150 kW，母線電壓保持穩定；圖10(b)中電機功率在0.6 s時由132 kW階躍至152 kW，系統崩潰。仿真結果再次驗證了理論預測結果的正確性。

圖10 Kp為0.4，負載功率階躍時系統仿真波形

從以上仿真結果可以得出，隨著Kp的增大，系統可帶電機負載功率逐漸增大，當Kp為0.4時，電機功率可達約150 kW，已經逼近源最大輸出功率174 kW，考慮開關管以及電機負載熱損耗的存在，繼續增大Kp對提高系統可帶電機負載功率最大值效果將不明顯。

4 結論

為研究車載綜合電力系統在大信號擾動下的失穩邊界問題，建立了系統的大信號模型，根據混合勢函數理論推導了系統的穩定域，考察了兩個重要參數對系統穩定域的影響規律，最后通過硬件在環仿真驗證。得到結論如下：

電機功率階躍值也會對系統的穩定域造成影響，ΔPload值越小，系統可帶電機負載功率值越大。

DC/DC變換器電壓環控制器比例系數Kp小于0.4時，增加Kp值能夠有效擴大系統穩定域，提高系統帶載能力；超過0.4后，受系統源輸出能力制約，提高效果不明顯。

通過混合式函數理論得到的車載綜合電力系統穩定域能夠有效預測評估系統的穩定性能。