一道2013年湖北高考題的不同解法引發(fā)的思考

楊雪蘋

（廣州大學(xué)附屬中學(xué)南沙實驗學(xué)校 廣東·廣州 511458）

0 引言

把問題的數(shù)量關(guān)系與空間形式結(jié)合起來考察，或者把圖形的性質(zhì)轉(zhuǎn)化為數(shù)量關(guān)系問題，這種處理問題的思想方法就是數(shù)形結(jié)合的思想方法。在學(xué)習(xí)和教學(xué)中，運(yùn)用數(shù)形結(jié)合的思想方法進(jìn)行解題，可以使得問題處理的更加簡單，便捷。一方面，借助于圖形的性質(zhì)可以將許多抽象的數(shù)學(xué)概念和數(shù)量關(guān)系形象化、簡單化，給人以直覺的啟示；另一方面，將圖形問題轉(zhuǎn)化為代數(shù)問題，以獲得精確的結(jié)論。

1 高考題引入

2 數(shù)形結(jié)合的轉(zhuǎn)換

2.1 由形到數(shù)的轉(zhuǎn)換

2.1.1 用向量法進(jìn)行轉(zhuǎn)換

上題中第二種解法就是數(shù)形結(jié)合里由形到數(shù)的轉(zhuǎn)換中的向量法，題中的式子表示的是空間幾何圖形，將幾何圖形向量化，運(yùn)用向量解決幾何中的問題，把抽象的幾何推理化為代數(shù)運(yùn)算，特別是空間向量法使解決立體幾何中平行、垂直、夾角、距離等問題變得有章可循。

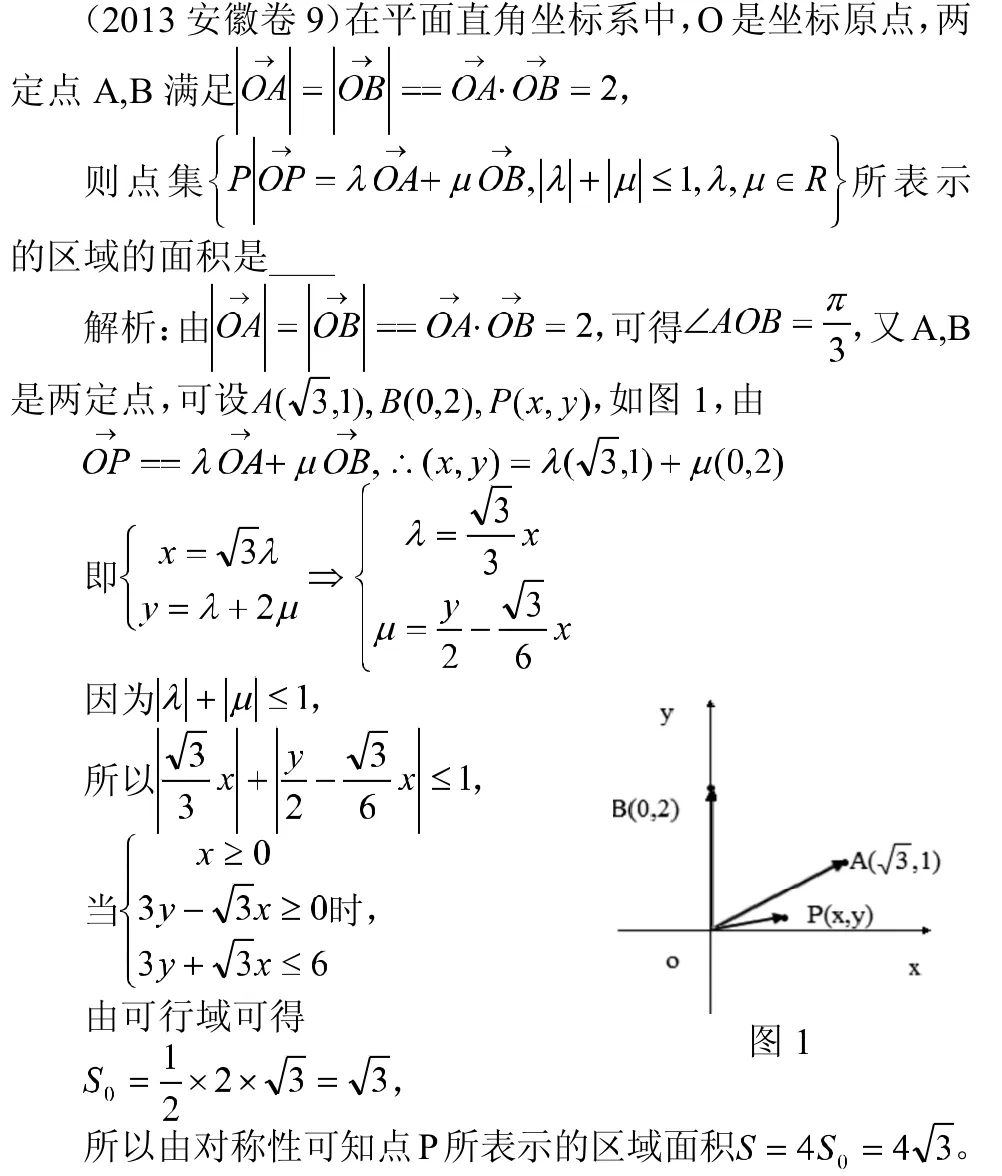
2.1.2 用解析法進(jìn)行轉(zhuǎn)換

建立適當(dāng)?shù)淖鴺?biāo)系引進(jìn)坐標(biāo)將幾何圖形變換為坐標(biāo)間的代數(shù)關(guān)系，把題目進(jìn)行由形到數(shù)的轉(zhuǎn)換，可以使得解題更加簡單。

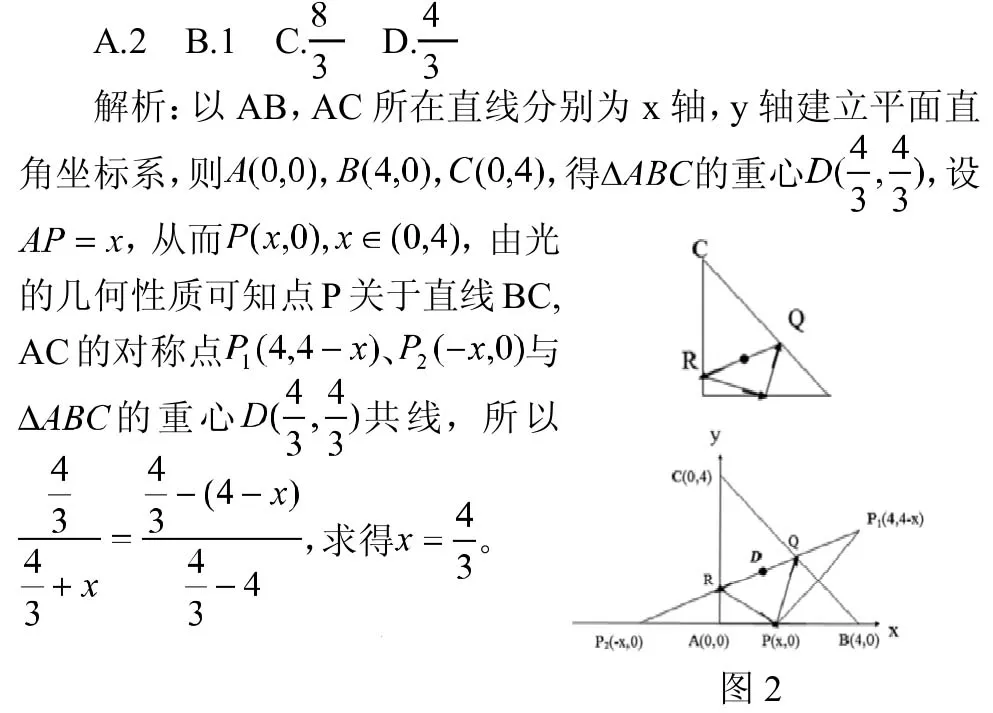
2.2 由數(shù)到形的轉(zhuǎn)換

2.2.1 與三角函數(shù)結(jié)合

利用數(shù)形結(jié)合解題不僅在高考題中出現(xiàn)，在一些競賽題目中也常常使用。

該題巧妙地運(yùn)用了數(shù)形結(jié)合思想，由不等式的形式構(gòu)造了圖形中兩點(diǎn)的距離，由數(shù)到形進(jìn)行轉(zhuǎn)化，使得解題變得簡單，在平常的做題中有很多這種數(shù)與幾何圖形結(jié)合的題型，比如數(shù)形結(jié)合求最值，數(shù)形結(jié)合與函數(shù)與方程等等，做題時一定要細(xì)心觀察，這樣才能使得解題得心應(yīng)手。

圖5

3 數(shù)形結(jié)合思想運(yùn)用的建議

數(shù)形結(jié)合法要求教師在長期的教學(xué)過程中潛移默化的讓學(xué)生掌握，僅僅靠幾節(jié)課、幾道例題，是不能使學(xué)生真正理解和掌握數(shù)形結(jié)合方法的，因此在教學(xué)中教師要經(jīng)常督促學(xué)生時刻學(xué)會運(yùn)用數(shù)形結(jié)合思想解題，在解題過程中要注意以下幾點(diǎn)：

第一，要善于觀察，在“由形到數(shù)”的轉(zhuǎn)換過程中，要注意說明圖形的特征、有哪些重要的點(diǎn)（特殊點(diǎn)）、有些什么性質(zhì)，以及性質(zhì)的來源等；

第二，要善于運(yùn)用，在“由數(shù)到形”的轉(zhuǎn)換過程中，要巧妙的運(yùn)用數(shù)的特點(diǎn)，構(gòu)造所需要的圖形，結(jié)合圖形的特殊性，找準(zhǔn)關(guān)鍵點(diǎn)所在，巧妙解答；

第三，在利用數(shù)學(xué)結(jié)合思想解題時，不能簡單構(gòu)造圖形，定義向量，一定要注意數(shù)的取值范圍，圖形的邊界。

4 小結(jié)

數(shù)形結(jié)合有利于提高思維的深刻性，因此，數(shù)學(xué)教學(xué)中，數(shù)形結(jié)合不應(yīng)僅僅作為一種解題方法，而應(yīng)作為一種基本的、重要的數(shù)學(xué)思想，作為數(shù)學(xué)知識的精髓，作為將知識轉(zhuǎn)化為能力的“橋”來學(xué)習(xí)研究和掌握應(yīng)用。

要將數(shù)形結(jié)合法運(yùn)用于解題教學(xué)和解題實踐作為解題方法的數(shù)形結(jié)合，實際上包括兩方面的內(nèi)容：一方面對“形”的問題，引入坐標(biāo)系或?qū)ふ移鋽?shù)量關(guān)系用向量方法表示，用“數(shù)”加以分析，即“由形到數(shù)”的轉(zhuǎn)換；另一方面對于數(shù)量關(guān)系的問題，分析其幾何意義，找出其中所反映的“形”之間的關(guān)系，借助形的直觀來解決。二者都是數(shù)形結(jié)合，不可偏廢。