透析2020年高考全國數學Ⅰ卷試題背后史料*

廣東省廣州市第九十七中學(510260) 徐進勇

《普通高中數學課程標準(2017年版)》指出:數學文化是指數學的思想、精神、語言、方法、觀點,以及它們的形成和發展;還包括數學在人類生活、科學技術、社會發展中的貢獻和意義,以及與數學相關的人文活動.數學教育應努力滲透數學史、數學家、數學精神和數學應用等數學文化要素以及廣泛的人文元素,感受數學價值,提升科學精神,培養應用意識,生成人文素養.新的高考評價體系旗幟鮮明地將“引導教學”作為高考的核心功能.2020 高考全國數學卷Ⅰ試題注重數學文化的融入,關注試題背后數學文化的建設與發展,這對提高學生整體數學文化素養起到積極作用.

第11 題(2020年高考全國Ⅰ卷理科)已知⊙M:x2+y2-2x -2y -2 = 0, 直線l:2x+y+ 2 = 0,P為l上的動點,過點P作⊙M的切線PA,PB,切點為A,B,當|PM|·|AB|最小時,直線AB的方程為( )

A.2x-y-1=0 B.2x+y-1=0

C.2x-y+1=0 D.2x+y+1=0

試題情境中的ΔPAB構成了圓的“阿基米德三角形”.阿基米德(公元前287-公元前212)是古希臘偉大的物理學家、數學家,他最早利用逼近思想解決封閉圖形的面積,體現了近代積分思想.他的數學貢獻史無前例,享有“數學之神”稱號.

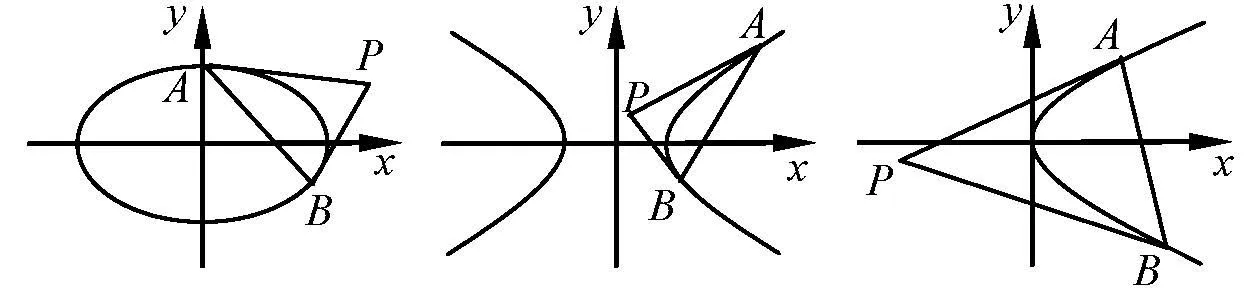
圖1

阿基米德三角形是指:過圓錐曲線上任意兩點A,B分別作兩條切線相交于點P,則稱ΔPAB為阿基米德三角形.其中∠P為頂角,AB為底邊,當AB過圓錐曲線焦點,此時ΔPAB叫阿基米德焦點三角形.圖1 分別為橢圓、雙曲線、拋物線的阿基米德三角形.

阿基米德三角形性質很多,下面我們擷取幾例.

性質1橢圓的阿基米德三角形中,弦端點處的兩條切線的交點P與橢圓中心的連線平分弦.

證明設A(x1,y1),B(x2,y2),P(x0,y0), 于是直線AP,BP的方程分別為:聯立解出x0=從而

設AB中點為Q, 則則kOQ=要證交點P與橢圓中心的連線平分弦AB, 只需證明kOP=kOQ, 即證即證即證顯然成立.所以kOP=kOQ,即OP平分AB.

同理, 圓和雙曲線的阿基米德三角形也有同樣的性質;拋物線的阿基米德三角形中,弦端點處的兩條切線的交點P與弦中點的連線平行拋物線的對稱軸.

因此,第11 題的解答可簡單作出判斷:因為AB⊥PM,|PM|·|AB|最小?四邊形APBM面積最小?PA最短?PM最短?PM⊥l?AB//l?答案應為B 或D,由圖可知AB的縱截距應為負,故選D.

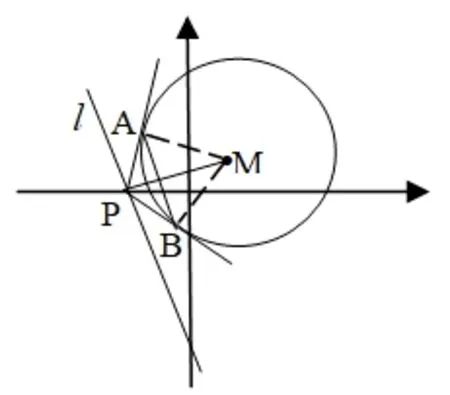
圖2

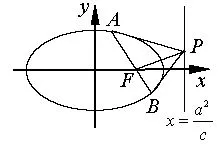
圖3

性質2如圖3,點P是橢圓= 1 過右焦點F的弦在兩端點處切線的交點,則P在橢圓的右準線x=上,且PF⊥AB,ΔPAB面積的最小值為

證明(1)設A(x1,y1),B(x2,y2),P(x0,y0),AB過右焦點F(c,0),于是直線AP,BP的方程分別為:=1和=1,聯立解出x0=又A,F,B三點共線,所以有(x1?=c,x2?=c),從而有x1y2-x2y1=c(y2-y1), 代入可得:x0=, 再解出于是當x1=x2=c時,易證所以點P在橢圓的右準線上運動.

雙曲線:如圖4, 點P是雙曲線過右焦點F的弦在兩端點處切線的交點,則P在雙曲線的右準線上,且PF⊥AB,ΔPAB面積的最小值為

拋物線:如圖5,點P是拋物線y2=2px過焦點F的弦在兩端點處切線的交點,則P在拋物線的準線x=-p上,且PF⊥AB,PA⊥PB,ΔPAB面積的最小值為p2.

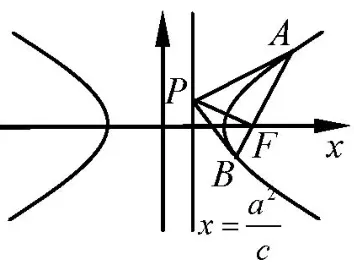
圖4

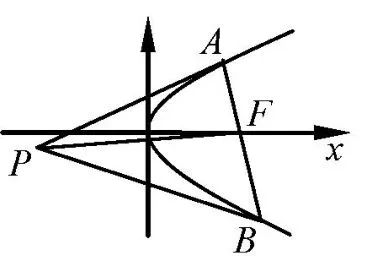
圖5

性質3當阿基米德三角形的頂角為直角時,對應的圓、橢圓、雙曲線有如下性質:對于圓x2+y2=r2,其阿基米德三角形頂點的軌跡為x2+y2=2r2;對于橢圓=1,其阿基米德三角形頂點的軌跡為x2+y2=a2+b2;對于雙曲線=1(a ＞b ＞0),其阿基米德三角形頂點的軌跡為x2+y2=a2-b2.

以橢圓為例證明:如圖6,當有一條切線和x軸垂直時,另一條和y軸垂直,其交點坐標為(±a,±b),它必定在圓x2+y2=a2+b2上.

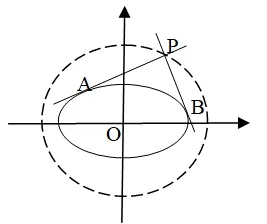
圖6

當兩條切線都不和坐標軸垂直時,可設兩條切線方程為PA:y=kx+m,PB:y=+n, 兩切線交點于是

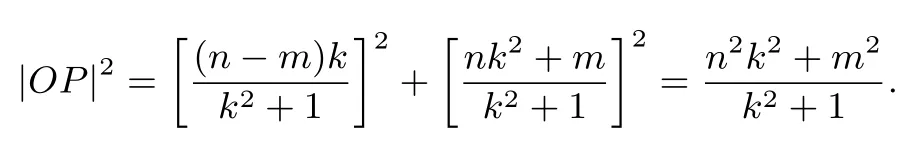
將PA的方程代入橢圓方程,得關于x的方程:因為直線與橢圓相切,所以Δ = 0,化簡可得m2=b2+a2k2.同理可得n2=b2+于是=a2+b2.

從以上三個結論可知, 無論是圓, 橢圓還是雙曲線,當頂角為直角時, 頂角P的軌跡方程均為圓, 我們稱這個圓為“蒙日圓”.2014年高考廣東卷20 題:已知橢圓= 1(a ＞b ＞0)的一個焦點為離心率為(1)求橢圓C的標準方程;(2)若動點P(x0,y0)為橢圓C外一點,且點到橢圓C的兩條切線相互垂直,求點P的軌跡方程.(答案(1);(2)x2+y2= 13.)此題的背景就是蒙日圓.

第19 題(2020年高考全國Ⅰ卷理科)甲、乙、丙三位同學進行羽毛球比賽,約定賽制如下:累計負兩場者被淘汰;比賽前抽簽決定首先比賽的兩人,另一人輪空;每場比賽的勝者與輪空者進行下一場比賽,負者下一場輪空,直至有一人被淘汰;當一人被淘汰后,剩余的兩人繼續比賽,直至其中一人被淘汰,另一人最終獲勝,比賽結束.經抽簽,甲、乙首先比賽,丙輪空.設每場比賽雙方獲勝的概率都為,(1)求甲連勝四場的概率;(2)求需要進行第五場比賽的概率;(3)求丙最終獲勝的概率.

解:(1)可作如下框圖分析:

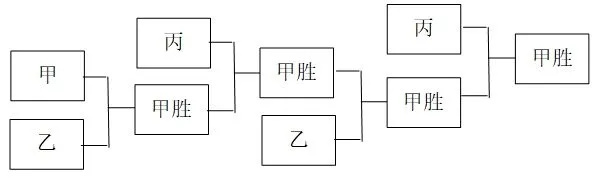
(2)根據賽制,至少需要進行四場比賽,至多需要進行五場比賽.比賽四場結束,共有三種情況:甲連勝四場的概率為乙連勝四場的概率為丙上場后連勝三場的概率為(甲、乙可輪換).所以需要進行第五場比賽的概率為

(3)丙最終獲勝,有兩種情況:比賽四場結束且丙最終獲勝的概率為比賽五場結束且丙最終獲勝,則從第二場開始的四場比賽按照丙的勝、負、輪空結果有三種情況:勝勝負勝,勝負空勝,負空勝勝,概率分別為因此丙最終獲勝的概率為.

回憶概率論起源問題:

1651年夏天,法國數學家、物理學家帕斯卡在一次旅行中,遇到了一個叫梅累的貴族公子,梅累經常出入賭場,梅累向帕斯卡請教了一個困擾很久的“賭金分配”問題:他和賭友擲骰子,各人下賭注32 個金幣,預定先贏三局為勝(梅累如果先擲出來三次6 點,或者賭友先擲出來三次4 點就算贏了對方),賭博進行了一段時間后,梅累已經兩次擲出來6 點(贏了2 局),而賭友已經擲出來一次4 點(贏了一局),這時梅累接到通知,要馬上去陪國王接見貴賓,賭博便只好中斷了,那么,留下的這64 個金幣兩人應該怎樣分才合理呢?

帕斯卡經過3年的冥思苦想,并與另外兩個大數學家費爾馬和惠更斯開展了熱烈的通信與討論,給出了邏輯嚴謹的正確解法,最后他們得出一致意見是:梅累應得到全部贖金的四分之三,對方得四分之一.這些信件就是最早的概率論文獻,這也是概率論的起源,所以早期概率論也被稱為“賭徒之學”.為什么這些大數學家會對一個賭博問題大感興趣,為它花費3年時間,還為此寫了一本叫《論賭博中的計算》的書? 正像惠更斯在書中所說的那樣:“任何一個讀者仔細觀察就會發現,這不僅僅是一個賭博問題.”

解法1:每一局(每一次投擲)甲勝的概率p1=乙勝的概率p2=平局的概率p3=

最終甲勝的情況包括以下兩種:

(1)平n局后甲勝一局,其概率和為:

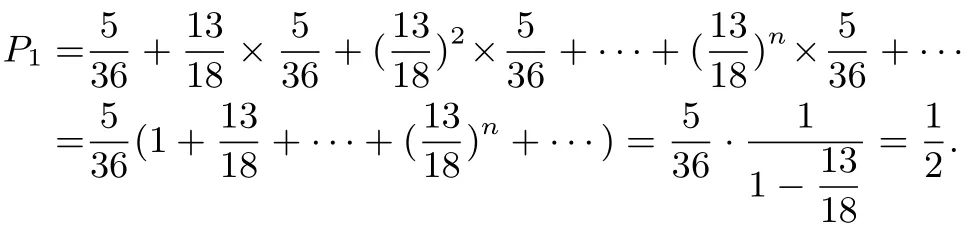
(2)平n局后甲輸一局,最后甲勝一局的概率和為:

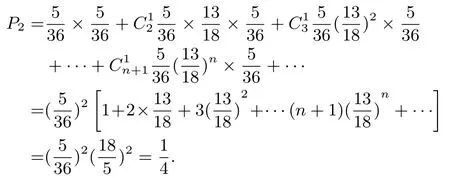
解法2若只考慮最后輸贏不考慮比賽場數時,平局可以不管,每一局甲、乙勝的概率相等,可均視為所以甲最終取勝可有下列兩種情況:

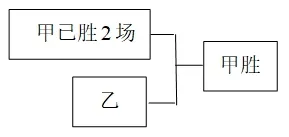
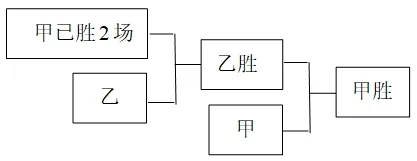
可見,今年概率題是以概率論起源問題為本源,充分體現概率論在實際中的應用價值,深刻考查了學生的邏輯推理能力.

化學家傅鷹指出:“一門科學的歷史是那門科學最寶貴的一部分,因為科學只能給我們知識,而歷史卻給我們智慧”.數學離不開數學歷史,數學歷史是數學的源頭.數學教育融入數學史料,可以呈現知識之諧,展示方法之美,營造探究之樂,揭示文化之魅,提供能力之柱,彰顯德育之效.