一類與函數零點個數有關問題的統一解法

廣東省佛山市南海區獅山石門高級中學(528225) 徐正印 白慶全

確定(討論)含有參數的函數零點的個數或根據含有參數的函數零點的個數確定(求)參數取值范圍的問題通常涉及到函數的單調性、最值等性質, 融合了數形結合、分離參數、等價轉化等數學思想方法,具有綜合性強、形式靈活、思維嚴密等特點,能較好地反映學生分析問題和解決問題的能力,備受高考命題者的青睞,在近年的新課標卷中持續出現.

由于“根據含有參數的函數零點的個數確定(求)參數取值范圍”可以看作是“確定(討論)含有參數的函數零點的個數”的逆運算,因此前者的本質與后者是一樣,他們可以看成是一類問題.

文[1]在延續了高考試題提供的解題思路的情況下,重點介紹了在使用零點存在定理時如何取“特殊點”,但這要具備較強的觀察能力,大部分考生(如筆者所面對的學生)不容易掌握其要領.

文[2]介紹了多種方法,同樣涉及“取點問題”,也需要較強的觀察能力.為此,筆者借助近年高考試題,對這類問題再次分析,以便讀者(考生)掌握其解題要領.

這類題目分兩種情況:

情況一可以分離參數,即利用含有參數(參數通常用a表示)的函數值等于零分離出參數,把函數零點的個數問題轉為一個不含參數的函數與一條與y軸垂直的動直線(通常為y=a)交點個數的問題,利用這兩個函數的圖象的交點的個數來確定(證明或討論)函數的零點的個數或確定(求)參數的取值范圍.如:

例1(2015年高考新課標Ⅰ卷文科)已知函數f(x)=e2x-alnx.

(Ⅰ)討論f(x)的導函數f′(x)的零點的個數;(Ⅱ)略.

例2(2018年高考新課標Ⅰ卷理科)已知函數f(x)=g(x)=f(x)+x+a,若g(x)存在2 個零點,則a的取值范圍是

A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)

例3(2018年高考新課標Ⅱ卷文科)函數f(x)=-a(x2+x+1).

(Ⅰ)略;(Ⅱ)證明:f(x)只有一個零點.

限于篇幅,僅以例1 為例說明.

分析 (Ⅰ)f′(x)= 2e2x-(x ＞0),f′(x)的零點的個數?方程2e2x-=0 正根的個數?2xe2x-a=0 正根的個數?y= 2xe2x(x ＞0)的圖象與y=a的圖象交點的個數.

設g(x)= 2xe2x(x ＞0), 則g′(x)= 2(1+2x)e2x, 在(0,+∞)上,g′(x)＞0,g(x)單調遞增.

g(x)= 2xe2x ＞0, 當x →0+時,g(x)→0;當x →+∞時,g(x)→+∞;函數y=2xe2x(x ＞0)的大致圖象如圖1.

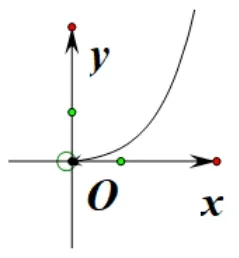
圖1

當a≤0 時,y= 2xe2x(x ＞0)圖象與直線y=a沒有交點;當a ＞0 時,y=2xe2x(x ＞0)圖象與直線y=a的圖象有且只有一個交點.綜上,當a≤0 時,f′(x)沒有零點;當a ＞0 時,有唯一的零點.

評注為了畫出y=g(x)的大致圖象(主要體現函數的單調性和趨向),需要先研究y=g(x)的單調性,再研究y=g(x)圖象的趨勢.

這種方法的優勢在于不需要找零點所在區間的端點.

例4(2016年高考新課標Ⅰ卷文科)函數f(x)=(x-2)ex+a(x-1)2.

(Ⅰ)略;(Ⅱ)若f(x)有兩個零點,求a的取值范圍.

例5(2018年高考新課標Ⅱ卷理科)已知函數f(x)=ex-ax2.

(Ⅰ)略;(Ⅱ)若f(x)在(0,+∞)上只有一個零點,求a.

例6(2020年高考新課標Ⅰ卷文科)已知函數f(x)=ex-a(x+2).

(Ⅰ)略;(Ⅱ)若f(x)有兩個零點,求a的取值范圍.

限于篇幅,僅以例4 為例說明.

在十九大開幕當天，江西日報全媒體報道中心策劃、中國江西網制作的H5作品“十九大報告學習詞典”發布。作品圍繞十九大，扣住報告中提出的“一系列新思想、新論斷、新要求”主線，圖文并茂，互動性強，6天時間總閱讀數就超過1000萬，成為全國媒體解讀十九大報告中少有的千萬級爆款作品。這是在重大事件報道面前，省級黨報集團媒體融合報道的一次有益嘗試和探索。

分析(Ⅱ)f(x)有兩個零點?(x-2)ex+a(x-1)2=0 有兩個實根?(x-2)ex+a(x-1)2=0 有兩個都不等于1 的實根?y=(x ?=1)的圖象與y=a的圖象有兩個不同的交點.

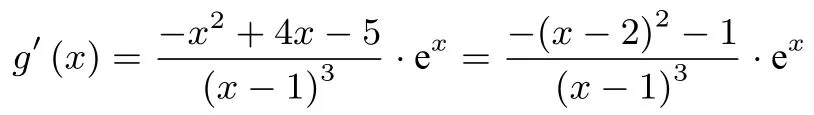
設g(x)=(x ?=1),則在 (-∞,1)上,g(x)＞0,g′(x)＞0,g(x)單調遞增.在(1,+∞)上,g′(x)＜0,g(x)單調遞減.當x → -∞時,g(x)→0; 當x →1-時,g(x)→+∞; 當x →1+時,g(x)→+∞;g(2)= 0; 函數的大致圖象如圖2.

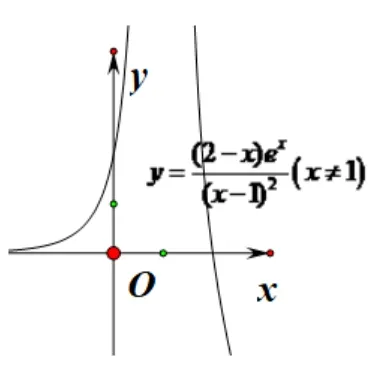
圖2

當a ＞0 時,y=的圖象與y=a的圖象有兩個不同的交點.故a的取值范圍是(0,+∞).

情況二不能分離或不便于分離參數(如分離出來的函數過于復雜),即利用含有參數(參數通常用a表示)的函數值等于零分離不出參數或不便于分離不出參數.

這類題目一般是這樣的:先要求考生討論函數的單調性;再要求考生根據這個函數零點的個數求參數的取值范圍.如:

例7(2017年高考新課標Ⅰ卷理科)已知函數f(x)=ae2x+(a-2)ex-x.

(Ⅰ)討論f(x)的單調性;

(Ⅱ)若f(x)有兩個零點,求a的取值范圍.

分析(Ⅰ)當a≤0 時,f(x)在R 上單調遞減;當a ＞0時,f(x)在單調遞減;f(x)在單調遞增(過程略).

(Ⅱ)由(Ⅰ)知:當a≤ 0 時,f(x)不可能有兩個零點.當a ＞0 時, 當x → -∞時,f(x)→+∞; 當x →+∞時,f(x)→+∞.因為f(x)有兩個零點, 所以

設g(x)=1-x-lnx(x ＞0),則g′(x)=在(0,+∞)上,g(x)單調遞減.因為g(1)= 0,所以當且僅當x ＞1 時,g(x)＜0, 即當且僅當時,故,a的取值范圍為(0,1).

例8(2020年高考新課標Ⅲ卷文科)函數f(x)=x3-kx+k2.

(Ⅰ)討論f(x)的單調性;

(Ⅱ)若f(x)有三個零點,求k的取值范圍.

分析(Ⅰ)當k≤0 時,f(x)在(-∞,+∞)上單調遞增; 當k ＞0 時, 在上單調遞減, 在上單調遞增(過程略).

(Ⅱ)當x →-∞時,f(x)→-∞; 當x →+∞時,f(x)→+∞.由(Ⅰ)知:欲使f(x)有三個零點, 則k ＞0,且綜上,k的取值范圍為