利用軌跡思想解三角形

廣東省佛山市羅定邦中學(xué)(528300) 龍 宇

廣東省佛山市順德區(qū)教師發(fā)展中心(528300) 王常斌

在高中階段解三角形問題,主要利用正弦定理與余弦定理.其數(shù)學(xué)思想是將幾何問題代數(shù)化,通過兩個定理將幾何關(guān)系轉(zhuǎn)化為一系列的方程,通過求解方程的解,再對所獲得的解進(jìn)行幾何解釋,這與解析幾何的思路是一致的.雖然利用正、余弦定理求解思維量較小,但運算量較大,且放棄了三角形的幾何性質(zhì).本文利用軌跡的思想,從“形”的角度來求解三角形問題.

一、構(gòu)造圓

(一)構(gòu)造外接圓

在初中階段,我們便熟悉定理:在圓中,直徑所對的圓周角為直角.逆向運用該定理,可發(fā)現(xiàn)在直角三角形中,當(dāng)斜邊長固定時,斜邊所對的頂點的軌跡為一個圓(去掉兩個點).

命題在ΔABC中, 角A,B,C所對的邊為a,b,c, 若邊a及角A為定值,則點A的軌跡為一段圓弧,特別地,當(dāng)A=90?時,對應(yīng)的軌跡為圓(去掉兩個點).

證明如圖1,設(shè)A為鈍角,以BC的中點O為原點,以BC為x軸,過點O作BC的垂線為y軸建立直角坐標(biāo)系.利用正弦定理:

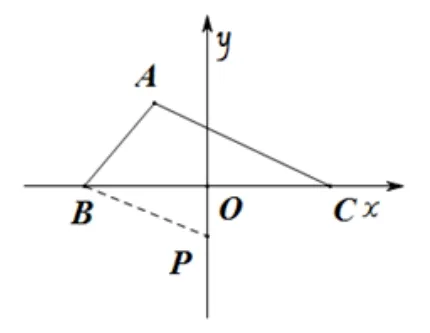
圖1

考慮ΔPBO,利用勾股定理可得:y=即可得ΔABC的外接圓的圓心頂點,半徑為定值,即ΔABC的外接圓為一個定圓,故可得點A的軌跡為劣弧BC.

當(dāng)A為銳角時, 則對應(yīng)的軌跡為優(yōu)弧BC, 特別地, 當(dāng)A=90?時,對應(yīng)的軌跡為圓(去掉兩個點).證畢

在高考中,也常常以該定理為背景進(jìn)行命題.

例1(2013年高考新課標(biāo)ⅠⅠ卷第17 題)在ΔABC中,內(nèi)角A,B,C的對邊分別為a,b,c,已知a=bcosC+csinB.

(1)求B;

(2)若b=2,求ΔABC面積的最大值.

例2(2014年高考新課標(biāo)Ⅰ卷第16 題)已知a,b,c分別為ΔABC的三個內(nèi)角A,B,C的對邊,a= 2, 且(2 +b)(sinA -sinB)= (c - b)sinC, 則ΔABC面積的最大值為____.

分析兩個問題的本質(zhì)相同, 根據(jù)題目的條件, 可確定ΔABC的一條邊及其對角.兩個問題都考查ΔABC面積的最值,常規(guī)的解題思路是結(jié)合正、余弦定理可將其轉(zhuǎn)化為三角函數(shù)的最值問題或不等式的相關(guān)問題.如果我們借助了上面的命題發(fā)現(xiàn)點A的軌跡,即可“秒殺”上述兩個問題.

以例1 為例, 由條件易得B=(過程略), 根據(jù)正弦定理:=2R,可得R=根據(jù)上面的定理,ΔABC的外接圓為定圓.如圖2, 設(shè)ΔABC的外接圓為⊙O.當(dāng)點B到直線AC的距離最大時,對應(yīng)的ΔABC的面積取到最大值.

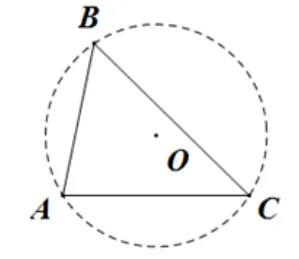
圖2

根據(jù)平面幾何的相關(guān)知識易得,當(dāng)BO⊥AC時,點B到直線AC的距離取到最大,對應(yīng)的最大值為:對應(yīng)的面積為同理可得:例2 的答案為證明過程留給讀者.

(二)構(gòu)造阿波羅尼斯圓

在平面上一點P到兩個定點A,B的距離之比滿足=λ(λ ＞0 且λ ?= 1),則點P的軌跡是圓,這個圓便是經(jīng)典的阿波羅尼斯圓.

例3(2008年年高考江蘇卷)滿足條件AB= 2,的ΔABC的面積的最大值是____.

分析本題使用正、余弦定理求解的難度很大,并且涉及不等式的放縮等技巧.如果利用軌跡的思想求解,本題的背景便是經(jīng)典的阿波羅尼斯圓問題.

解析如圖3,以AB的中點O為原點進(jìn)行建系, 則點A,B的坐標(biāo)為(-1,0), (1,0), 設(shè)點C的坐標(biāo)為(x,y)代入條件AC=化簡可得點C的軌跡方程為:(x-3)2+y2=8,即圓心為E(3,0),r=的圓.

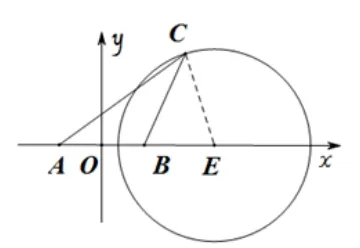
圖3

ΔABC的面積的最大值問題則轉(zhuǎn)化為點C到x軸距離的最大值問題.根據(jù)平面幾何的相關(guān)知識可知,點C到x軸距離≤CE=對應(yīng)的ΔABC的面積的最大值為

(三)構(gòu)造一般的圓

在一些解三角形問題中,可能沒有出現(xiàn)明顯的幾何特征顯示出圓,但只要我們使用軌跡的思想思考問題,會發(fā)現(xiàn)一些隱藏的“圓”.

例4在平面四邊形ABCD中,AB= 1,AC=BD⊥BC,BD=2BC,求AD的最小值.

分析本題可用的解法較多,利用正、余弦定理求解難度較大,且不夠直觀.利用軌跡的思想則可以清晰的理解各個條件的意義.

解析利用軌跡法求解的第一個難點在于坐標(biāo)系的建立,本題中有BD⊥BC,容易想到以點B為原點建立平面直角坐標(biāo)系,設(shè)點A的坐標(biāo)為(1,0),以點A為圓心,√為半徑構(gòu)造⊙A,顯然可得:C ∈⊙A,具體如圖4-1.接下來,構(gòu)造點D,將點C繞點B旋轉(zhuǎn)得到C1,延長BC1至D,使得BD=2BC1.

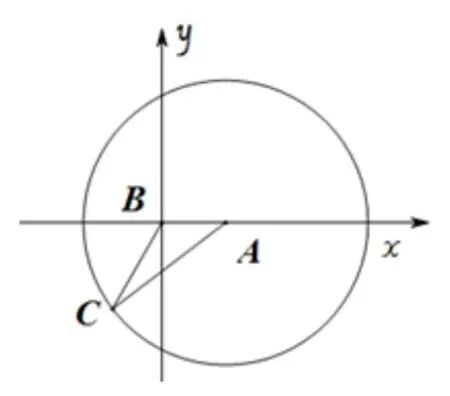
圖4-1

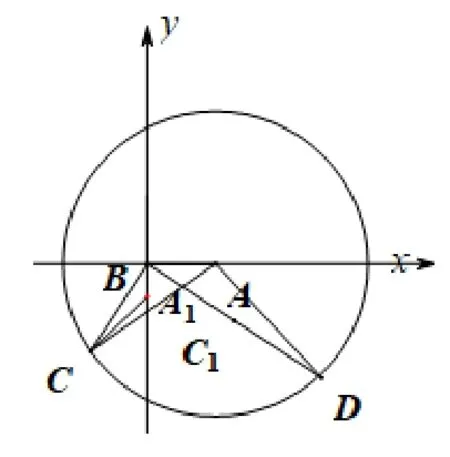
圖4-2

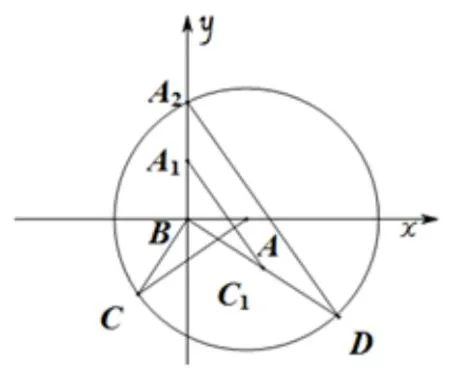
圖4-3

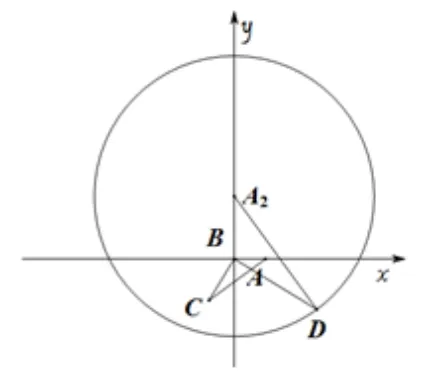
圖4-4

方法1取A1(0,), 連接DA,CA1,A1B, 如圖4-2.易得∠ABD= ∠A1BC,又因為BA= 2BA1,BD= 2BC,所以ΔABD∽ΔA1BC,所以DA= 2CA1,由此可得DA的最小值為CA1最小值的2 倍,又AA1=,AC=所以當(dāng)且僅當(dāng)C,A1,A三點共線時,CA1有最小值,從而AD的最小值為

方法2為了方便敘述點D的軌跡, 我們將點A也進(jìn)行如上操作(將點A繞點B旋轉(zhuǎn), 得到A1(0,1), 記A2(0,2)), 具體如圖4-3.易得ΔBA1C1∽= ΔBAC, 所以A1C1=AC=√又C1,A1分別是BD,BA2的中點,所以A2D= 2A1C1=由此可得點D的軌跡為以A2(0,2)為圓心,為半徑的圓,記為⊙A2,如圖4-4.

接下來,原問題轉(zhuǎn)化為求⊙A2上一點D到點A距離的最小值.與圓上點有關(guān)的最值問題,可借助圓心求得:AD的最小值為√最大值為

二、構(gòu)造橢圓

當(dāng)三角形中出現(xiàn)定點或定長時,我們也可結(jié)合其他的圓錐曲線進(jìn)行思考.2013年課標(biāo)全國1 卷第12,構(gòu)造了一系列的三角形,考查三角形面積的變化規(guī)律.常規(guī)的解法運算量都較大,當(dāng)我們使用軌跡的思想時,即可構(gòu)造一個橢圓,通過橢圓的相關(guān)性質(zhì)進(jìn)行判斷.

例6 [1](2013 高考課標(biāo)Ⅰ卷理科第12 題)設(shè)ΔAnBnCn的三邊長分別為an,bn,cn, ΔAnBnCn的面積為Sn,n= 1,2,3,···.若b1＞c1,b1+c1= 2a1,an+1=an,則( ).

A.{Sn}為遞減數(shù)列

B.{Sn}為遞增數(shù)列

C.{S2n-1}為遞增數(shù)列,{S2n}為遞減數(shù)列

D.{S2n-1}為遞減數(shù)列,{S2n}為遞增數(shù)列

解析因為an+1=an=an-1=···=a1, 所以ΔAnBnCn的一個邊是固定的, 又因為bn+1=可通過數(shù)學(xué)歸納法證得:bn+1+cn+1=bn+cn=···=b1+c1=2a1.即ΔAnBnCn另兩條邊之和為定值.

如圖5,對ΔAnBnCn而言, 以BnCn的中點O為原點,OCn為x軸,過O做OCn的垂線為y軸.點Bn的坐標(biāo)為點Cn的坐標(biāo)為設(shè)點An的坐標(biāo)為(x,y),因為AnBn+AnCn等于定值,所以點An的軌跡為橢圓(去掉兩個端點),其橢圓方程為:=1(y ?=0).

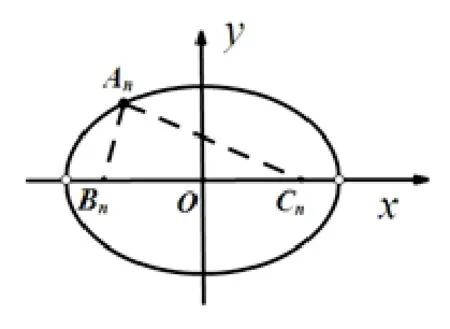
圖5

顯然可得:|bn+1-cn+1|=所 以 當(dāng)n增大時, 點An向橢圓的上頂點靠近.根據(jù)面積公式:即有Sn隨著yAn的增大而增大,故{Sn}為遞增數(shù)列.

三、構(gòu)造雙曲線

例7在ΔABC中,內(nèi)角A,B,C的對邊分別為a,b,c,a=4,sinA+2 sinB=2 sinC,求的最小值.

分析受上文構(gòu)造橢圓的提示,當(dāng)出現(xiàn)兩邊只差為定值時,我們還可以構(gòu)造出雙曲線進(jìn)行求解.結(jié)合雙曲線的軌跡方程即可實現(xiàn)對目標(biāo)式的化簡.

解析根據(jù)條件及正弦定理可得:a+2b= 2c,整理可得:c-b== 2.由此以BC的中點為原點建立直角坐標(biāo)系,點B,C的坐標(biāo)為(-2,0),(2,0),點A的軌跡為雙曲線的一支.

根據(jù)以上信息易得點A的軌跡方程為:x2-=1(x ＞0).根據(jù)對稱性,本文僅考慮上半部分.設(shè)點A的坐標(biāo)為(x,y),利用焦半徑公式可得:AB=2x+1,AC=2x-1.結(jié)合三角函數(shù)的定義可得:sinB=,sinC=因此得到:

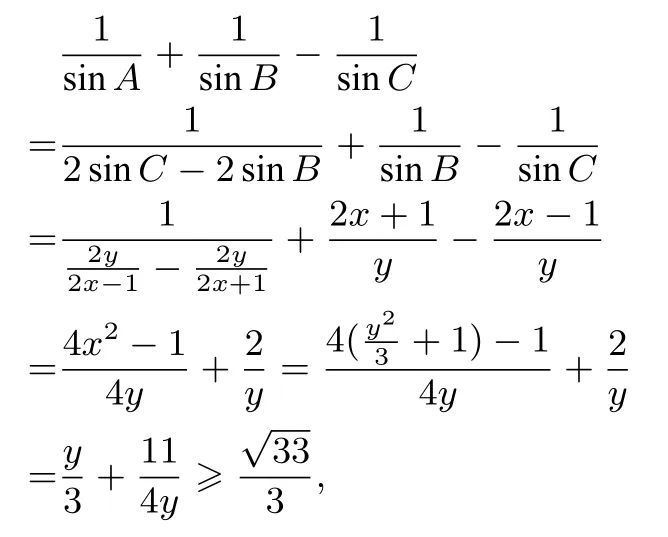
四、練習(xí)

1.在ΔABC中, 內(nèi)角A,B,C的對邊分別為a,b,c,a=b2+c2= 24, 求ΔABC面積的最大值.(答案:

2.(2016年佛山一模第16 題)在ΔABC中, 角A、B、C所對的邊分別為a、b、c,M是BC的中點,BM= 2,AM=c-b,則ΔABC面積的最大值為____.(答案:.)

3.(2019年佛山一模第16 題)在ΔABC中,角A、B、C所對的邊分別為a、b、c,且a=1,A=.若當(dāng)b,c變化時,g(b,c)=b+λc存在最大值,則正數(shù)λ的取值范圍是____.(答案: