“創新性”探究*
——一道開放性試題引起的思考

廣東省中山市楊仙逸中學(528400) 謝榕平

《中國高考評價體系》中的“四層”考查內容和“四翼”考查要求,是通過情境與情境活動兩類載體來實現的.高考通過設置不同層級的情境活動來考查學生在“四層”內容上的表現水平.根據“四翼”考查要求,高考命題需要體現基礎性、綜合性、應用性和創新性.創新性要求創設合理情境,設置新穎的試題呈現方式和設問方式,要求即將進入高等學校的學習者能在新穎或陌生的情境中主動思考,完成開放性或探究性的任務.

基于《中國高考評價體系》對于試題在創新性方面的要求,中學教育在試題命制上也做了大膽的探索和嘗試,打破常規命題規律, 采用新穎、靈活的方式, 以期對教學有一個較好的引導作用.在最近一次較大型考試活動中,出現了一道開放性題目,筆者就題目的形式、閱卷過程發現的問題和2020年高考數學試題中出現的開放性題型做一個探討研究,以期交流.

1 試題展示及評析

題目數學命題一般由“條件”和“結論”兩部分組成.正確的命題揭示了“條件”與“結論”之間的必然聯系.如果我們把命題中“條件”和“結論”互換身份,就有可能得到一個有意義的逆向命題;把一個數學命題中的某些特殊的條件一般化(比如取消某些條件過強的限制),從而得到更普遍的結論,叫做數學命題的推廣.這兩種方式都是發現數學新知識的重要途徑.下面,給出一個具體問題,請你先解答這個問題,并嘗試按上面提示的思路,提出有意義的問題并解答.

圓O的方程為x2+y2= 1,斜率為k的直線l與圓O交于兩點A,B,與x軸交于圓內一點F(c,0),其中c ?=0,點M(m,0)為x軸上一點.

(1)當c=,k= 2 時,若有∠OMA= ∠OMB,求m的值;

(2)就本問題,請你嘗試提出有意義的問題并解答(請注意完整、清晰、簡潔地敘述你所提出的問題.本題視所提問題的意義及解答給分).

試題第一問給定了參數求解,難度較低,給大部分考生成功求解的機會.第二問以開放性的形式呈現,需要考生自己提出問題然后再解答,評分視所提問題及解答水平層次而定.試題很好地考查了學生數學運算、直觀想象、數學抽象的核心素養,同時也考查了學生轉化與化歸、從特殊到一般的數學思想方法.題目既體現了基礎性和綜合性,考查了學生直線與圓的基礎知識、基本技能,又體現了創新性,高度符合《中國高考評價體系》對試題的命制要求.

2 解答探究

2.1 第(1)問解答當c=,k= 2 時,A,B兩點坐標為(0,-1),由kAM+kBM=得m=2.

2.2 第(2)問解答根據不同層級思維水平,第(2)問的解答可能會出現如下情況:

2.2.1 第一類(逆命題或參數變化)此類解答只是把問題變為逆命題或者改參數為其它特殊值,思維水平層次較低,在評分時得分就會較低.

參考1(逆命題)問題:圓O的方程為x2+y2= 1,斜率為k的直線l與圓O交于兩點A,B,與x軸交于圓內點F(c,0),點M(m,0)為x軸上一點.當c=,k= 2 時,若m=2,則有∠OMA=∠OMB.

參考2(改變k)問題:圓O的方程為x2+y2= 1,斜率為k的直線l與圓O交于兩點A,B,與x軸交于圓內點F(c,0),點M(m,0)為x軸上一點.當c=,k= 1(或者k為其它具體常數)時,若有∠OMA=∠OMB,求m的值.

參考3(改變c)問題:圓O的方程為x2+y2= 1,斜率為k的直線l與圓O交于兩點A,B,與x軸交于圓內點F(c,0),點M(m,0)為x軸上一點.當c=,k= 2(或者c為其它具體常數)時,若有∠OMA=∠OMB,求m的值.

2.2.2 第二類(參數一般化)這一類解答是把一個參數一般化,或者寫成其逆命題的形式,思維水平層次比第一類解答的思維水平層次高.

參考4(參數k 一般化)問題:圓O的方程為x2+y2=1,斜率為k的直線l與圓O交于兩點A,B,與x軸交于圓內點F(c,0),點M(m,0)為x軸上一點.當c=時,若對任意常數k,有∠OMA=∠OMB,求m的值.

逆命題:圓O的方程為x2+y2= 1,斜率為k的直線l與圓O交于兩點A,B, 與x軸交于圓內點F(c,0), 其中c ?= 0,點M(m,0)為x軸上一點.當c=,m= 2 時,則對任意常數k,有∠OMA=∠OMB.

解答過程:證明:當直線斜率為0 時顯然成立; 當斜率不為0 時, 設t=,A(x1,y1),B(x2,y2),AB的方程為x=ty+,代入圓的方程整理得:(t2+1)y2+ty+(-)=0,而

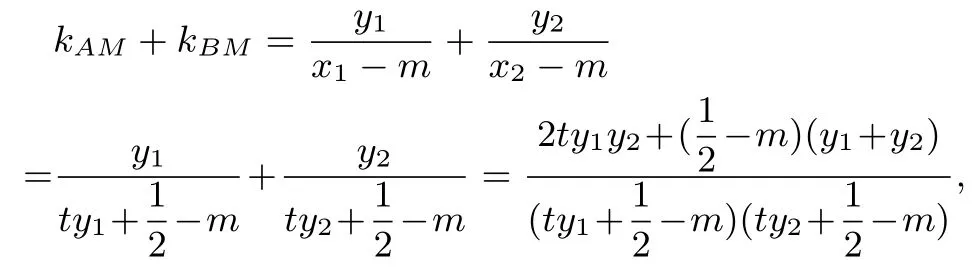
其中

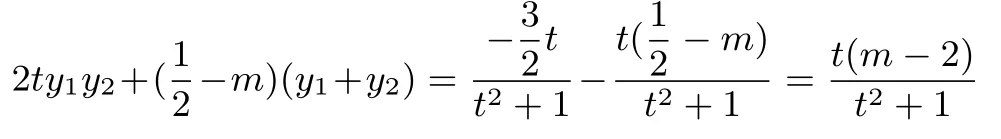
由于t是任意非零實數,所以∠OMA= ∠OMB等價于kAM+kBM=0,即m-2=0,即m=2,反之亦然.

參考5(參數c 一般化)問題:圓O的方程為x2+y2=1,斜率為k的直線l與圓O交于兩點A,B,與x軸交于圓內點F(c,0),其中c ?= 0,點M(m,0)為x軸上一點.當k= 2時,若有∠OMA=∠OMB,求m的值.

逆命題:圓O的方程為x2+y2= 1, 斜率為k的直線l與圓O交于兩點A,B, 與x軸交于圓內點F(c,0),其中c ?= 0, 點M(m,0)為x軸上一點.當k= 2 時, 若(-1＜c ＜1 且c ?=0),則有∠OMA=∠OMB.

解答過程:證明:設A(x1,y1),B(x2,y2),AB的方程為代入圓的方程整理得:y1+y2=而

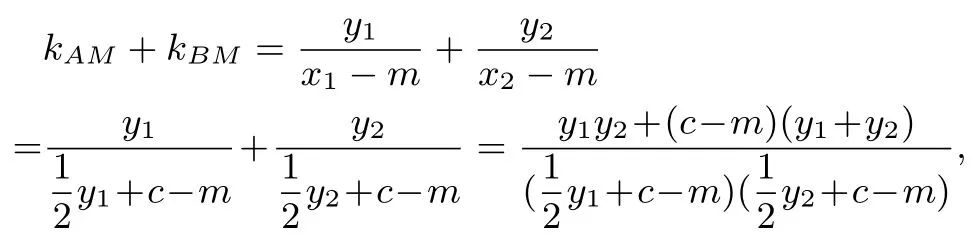
其中

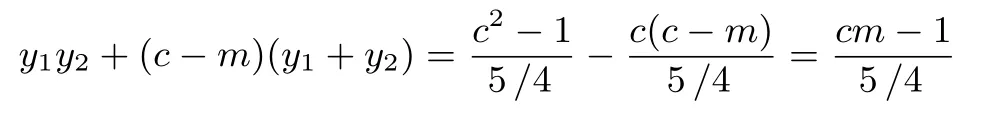
因為∠OMA= ∠OMB等價于kAM+kBM= 0, 即cm-1=0,即m=反之亦然.

2.2.3 第三類(問題一般化)

這一類解答是把問題一般化,思維層次水平較高.能較好的考查學生由數字運算到字母運算的能力的達成,極好滲透由特殊到一般的數學思想方法.

參考6(參數c,k 一般化)問題:圓O的方程為x2+y2= 1, 直線l與圓O交于兩點A,B, 與x軸交于圓內點F(c,0), 其中c ?= 0, 點M(m,0)為x軸上一點.當mc=1 時,都有∠OMA=∠OMB.

注事實上,本問題中mc=1 與∠OMA=∠OMB是充要條件,給出充要條件者亦記滿分.

解答過程:圓O的方程為x2+y2=1,直線l與圓O交于兩點A,B,與x軸交于圓內點F(c,0),點M(m,0)為x軸上一點.則對任意k有∠OMA= ∠OMB成立的充要條件為mc=1.

證明:設A(x1,y1),B(x2,y2),AB的方程為x=ty+c,代入圓的方程整理得:(t2+ 1)y2+ 2tcy+c2-1 = 0,而

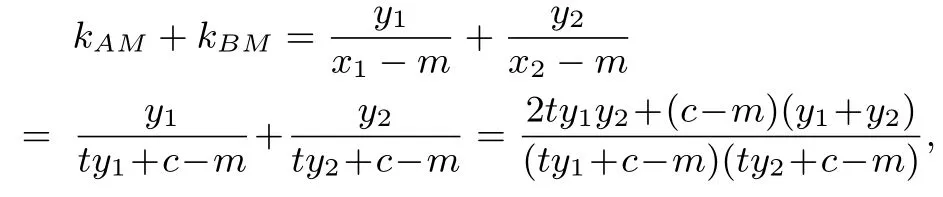
其中

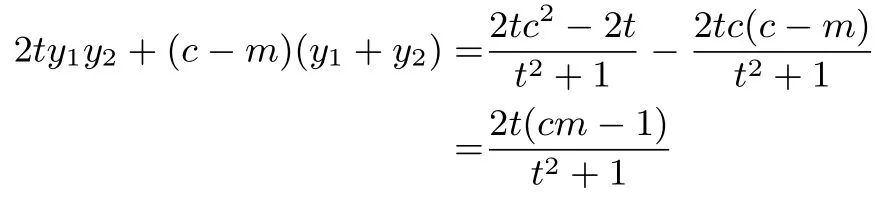
由于t是任意實數, 所以∠OMA= ∠OMB等價于kAM+kBM=0,即cm-1=0,即cm=1,反之亦然.

3 學生典型問題剖析

本試題的命制在創新性上是一個很有意義的嘗試,在閱卷過程中暴露出學生較多的問題.

3.1 必備知識不少學生卷面出現直線方程寫錯、計算出錯等問題,反映出學生的基本概念、基本原理、基本技能掌握不扎實.對解析幾何中坐標法的思想領悟不到位,角度相等只能直觀翻譯為角平分線,不能轉化到坐標上.

3.2 關鍵能力對于第(2)問的解答,絕大部分學生只能依葫蘆畫瓢,停留在改變參數這個低層次的思維模式,提出的問題還是原來題設的問題;學生沒能發現題目已經以字母化的形式表示了一定量,命題者的原意就是需要考生進行抽象加工為一般化;部分學生能發現與斜率無關,寫出動直線的原命題和逆命題,但還未發現一般化的推廣.從以上這些閱卷情況可以發現,學生的關鍵能力,特別是符號理解能力、信息轉化能力、抽象思維能力等還比較欠缺,沒能從所給情境中提取有效信息,透過現象看到本質,發現隱含的規律.

3.3 學科素養本題如果以一個常規題型的形式呈現,學生順利解答就相對容易很多,現在以開放式的學習探索情境出現,學生無法掙破常規思維的桎梏,無從下手.有些同學提出的問題是求切線方程,求弦長,求圓的標準方程等,說明學生沒有擺脫平時題目訓練的痕跡,思維局限在刷的題目里,其本質上是缺少理性思維、數學應用和數學探索的能力,也是題海戰術和套路訓練的必然結果.這是日常教學的薄弱點,也是該改進和努力的地方.

4 高考試題展示

高考數學的創新性強調對知識的靈活運用,通過命制開放性試題,結構不良試題等,發揮選拔功能.2020年的高考試題里也有新穎的創新題型出現,如2020年高考數學山東卷、海南卷第17 題:

在1○ac=√2○csinA= 3, 3○c=這三個條件中任選一個,補充在下面問題中,若問題中的三角形存在,求c的值;若問題中的三角形不存在,說明理由.

問題是否存在ΔABC,它的內角A,B,C的對邊分別為a,b,c,且sinA=

注:如果選擇多個條件分別解答,按第一個解答計分.

從試題形式上看,這是一道創新的開放性題目,也是一道結構不良題目.從內容上看,作為一道解三角形的題目,不管是三個條件中的哪一個,放進問題里作為一道常規的高考試題,都是一道不難的題目,選擇條件①或者②,所求三角形都是存在的,選擇條件③,所求三角形不存在.但這種打破常規的題型設置從主觀上已經把相當一部分學生嚇到,讓學生無所適從.這種創新性的題型,主要考查學生的探究能力、理性思維和邏輯思維能力,有較好的區分度,有利于人才選拔.面對這種新穎、靈活的命題趨勢,不管是教師的教還是學生的學,都要解決高考備考中的“阿喀琉斯之踵”,改變應試教育一味刷題的學習模式,從套路訓練中跳出來.日常教學和備考都要注意抽絲剝繭,把握數學本質,強調能力的培養,培養學生高層次的理性思維和敢于質疑、勇于創新、提出獨特見解的可貴品質.

5 結束語

基于高考評價體系,高考命題理念實現了由“知識能力立意”到“價值引領、素養導向、能力為重、知識為基”的轉變.“四翼”考查要求里的創新性是高考選拔功能的體現,鼓勵學生擺脫定勢思維的束縛,從整體上建構知識框架,形成深層次的認知結構,加強邏輯思維能力的培養,提升分析問題、解決問題的能力,引導、啟發學生探索生活中的數學問題,促進學生的實踐能力,在學習、積累、領悟、內省、升華中形成數學學科核心素養.