對一道高考不等式證明題的探究

湖南省懷化市湖天中學(418000) 宋林潔

湖南省會同縣第一中學(418300) 于先金

一、高考真題,簡潔優美

2020年高考全國Ⅲ卷文、理第23 題:設a,b,c ∈R,a+b+c=0,abc=1.

(1)證明:ab+bc+ca ＜0;

(2)用max{a,b,c}表 示a,b,c的最大值,證明:max{a,b,c}≥

這道試題簡潔、對稱、新穎、優美,難度不大,主要考查不等式的證明及基本不等式的應用,考查的核心素養是邏輯推理和數學運算,值得我們去思考和探究.

二、參考答案,通性通法

證明(1)由題設可知a,b,c均不為零,所以

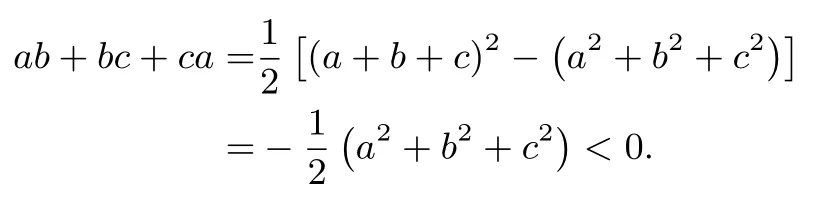
(2)不失一般性,不妨設a≥b≥c,所以max{a,b,c}=a, 因為abc= 1,a=-(b+c), 所以a ＞0,b ＜0,c ＜0.由bc≤可得abc≤故a≥所以max{a,b,c}≥

三、證法探究,數學好玩

1.第(1)問的證法探究

由已知條件a+b+c=0 與待證結論ab+bc+ca ＜0,易想到代入消元.

證法1(代入消元,分而治之)

由a+b+c=0 得a+c=-b,所以ab+bc=b(a+c)=-b2.同理可得bc+ca=-c2,ab+ca=-a2.以上三個不等式相加并整理得ab+bc+ca=(a2+b2+c2)＜0.

由已知條件a+b+c=0 與待證結論ab+bc+ca ＜0,易想到不等式a2+b2+c2≥ab+bc+ca.

證法2(結構聯想,平方解決)

由已知條件a+b+c=0 與abc=1,可知a=b=c不可能.又a2+b2+c2≥ab+bc+ca,當且僅當a=b=c時等號成立, 所以a2+b2+c2＞ ab+bc+ca.所以(a+b+c)2=a2+b2+c2+2(ab+bc+ca)＞3(ab+bc+ca)所以ab+bc+ca ＜0.

由a+b+c、abc及ab+bc+ca的結構特征,自然聯想到一元三次方程的韋達定理.

證法3(韋達定理,構造方程)

設ab+bc+ca=m,又由已知a+b+c= 0,abc= 1,可知a,b,c是方程x3-0·x2+mx-1=0 的三個根,且a,b,c中一正兩負,不妨設a ＞0,b ＜0,c ＜0.當x=b(b ＜0)時,有所以ab+bc+ca ＜0.

2.第(2)問的證法探究

不失一般性,不妨設a≥b≥c,所以max{a,b,c}=a,又a+b+c= 0,abc= 1,所以a ＞0,b ＜0,c ＜0.所以只要證明由已知條件含有和、積的結構,欲證結論又是不等式,自然聯想到利用一些基本不等式.

證法1(利用均值,馬到成功)

由(-b)+ (-c)≥得a≥解得易知當且僅當b=c=時等號成立.

證法2(不等放縮,同樣精彩)

由a+b+c=0,得a=-(b+c),所以

a2=(b+c)2=b2+c2+2bc≥2bc+2bc=4bc=所以a3≥4,解得a≥

證法3(柯西登場,建立不等)

由a+b+c= 0, 得b+c=-a, 兩邊平方并整理得b2+c2=a2-2bc=a2-由柯西不等式得b2 +c2≥所以即a3≥4, 解得

由x2+y2=R2(R ＞0),可設x=Rcosθ,y=Rsinθ,于是有如下的三角換元.

證法4(三角換元,直達目的)

由證法3, 可設-b=sinθ,θ ∈所以

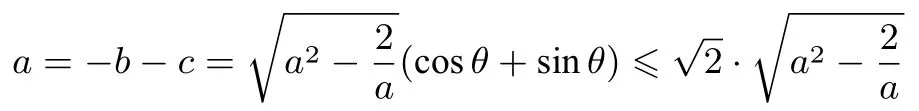
證法5(三角換元,拍案叫絕)

由a+b+c=0,得(-b)+(-c)=a,可設-b=acos2θ,-c=asin2θ,所以

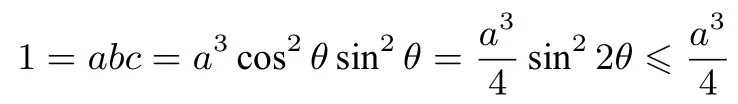
證法6(構造方程,判別式法)

由已知條件可得b+c=-a,bc=所 以b,c是一元二次方程x2+ax+= 0 的兩個根, 所以判別式解得

證法7(確定主元,構造方程)

由a+b+c=0,得b=-(a+c),代入abc=1 并整理得ac2+a2c+1=0,可視為關于c的一元二次方程,所以判別式Δ=a4-4a≥0,解得a≥

證法8(數形結合,殊途同歸)

因為a ＞0,b ＜0,c ＜0, 所以雙曲線與直線b+c+a=0 在直角坐標系boc的第三象限有公共點(圖略),所以雙曲線在第三象限的頂點在直線b+c+a= 0 上或其上方,所以解得

四、繼續探究,加強結論

經探究,對(1)中的不等式ab+bc+ca ＜0,我們得到如下的加強:設a,b,c ∈R,a+b+c= 0,abc= 1.證明:ab+bc+ca≤

證法1(恒等變形,不等放縮)

不失一般性,不妨設a≥b≥c,由(2)得當且僅當b=c=時等號成立.由(1)的參考答案可得

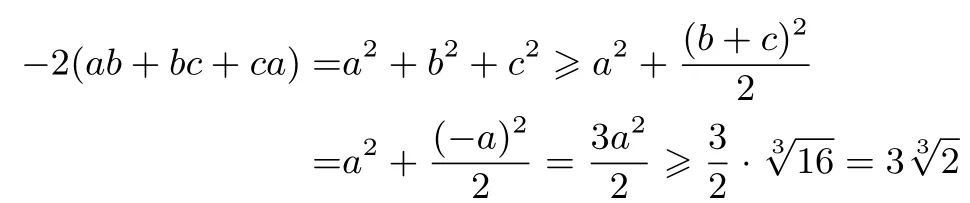
所以ab+bc+ca≤當且僅當時等號成立.

證法2(恰當配湊,均值放縮)

因為

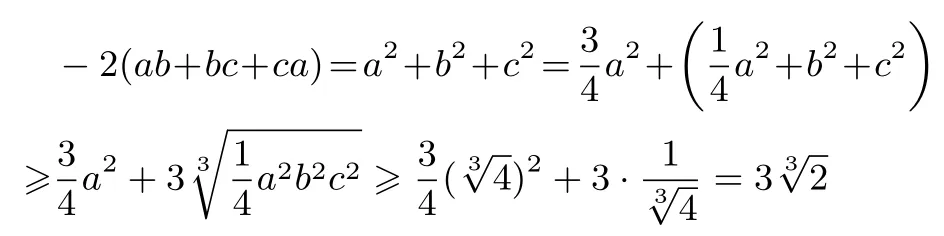
所以ab+bc+ca當且僅當時等號成立.

五、變式探究,精彩紛呈

變式1設a,b,c ∈R,a+b+c= 0,abc= 1.用min{a,b,c}表示a,b,c的最小值,則min{a,b,c}≤

證明(利用結論,一步到位)

不失一般性,不妨設a≥b≥c,由(2)得當且僅當b=c=時等號成立.所以-2c≥-b-c=a≥所以c≤即min{a,b,c}≤

變式2 設a,b,c ∈R,a+b+c= 0,a2+b2+c2= 1,則a,b,c ∈

變式3設a,b,c ∈R,a+b+c=m(m ＞0),a2+b2+c2=則a,b,c ∈

變式2、變式3 易證,證明略.

變式4設a,b,c ∈R,abc= 1,ab+bc+ca=則a+b+c≤0.

證明(確定范圍,利用單調)

不失一般性, 不妨設a≥b≥c, 所以由已知條件易知a ＞0,b ＜0,c ＜0.設a+b+c=λ, 則由ab+bc+ca=及abc=1 可得a(b+c)+bc=即a(λ-a)+所以λ=a-(a ＞0).

求導可得λ′= 1 +＞0, 所以函數λ=a -在區間(0,+∞)上單調遞增.因為(-b)+(-c)≥又a(b+c)+bc=所以

由上可知,λ≤故a+b+c≤0.

下面提出一個問題,供讀者進一步探究:

問題1設a ＞0,b ＞0,c ＞0,a+b+c=m(m≥3),abc=1,你能得到一些什么樣的結論?

六、一點思考

2002年, 陳省身在世界數學家大會上為少年兒童題詞“數學好玩”,如何讓學生在數學學習中體會到“數學好玩”,在“玩”中學好數學,這是值得我們認真思考的一個問題.

數學是美的,數學是自然的,其中的數學概念、數學方法與數學思想的起源與發展都是自然的.北京大學張筑生教授在很早就呼吁:“讓解題的思路來的自然.”一些自然的解法之所以自然,是因為它透過現象抓住了問題的本質.在數學解題和數學教學中,我們應該從學生已有的知識基礎和經驗出發,去尋找自然的解法.

在教學中,我們不僅要教會學生如何思考問題,還要引導學生學會提出問題,為學生提供微探究的機會.