從圓的反演變換到橢圓的反演變換

華南師范大學附屬中學(510631) 羅碎海

平面幾何中的反演變換是相當有趣的數學知識,它實現了圓與直線的轉化.學習了橢圓后,自然想到,這種反演變換能否推廣到橢圓中.

1 反演變換及其性質

1.1 反演變換定義及其幾何作圖

定義1在平面π上, 設O是一個定點,P,Q是射線Ox上的兩點, 且滿足條件OP ·OQ=r2, 我們稱P與Q互為反演點,這個變換稱為平面π的一個反演變換,記做I(O,r2).定點O稱為反演中心(反演極),r叫做反演半徑,以O為圓心、r為半徑的圓叫反演基圓,r2叫反演冪.

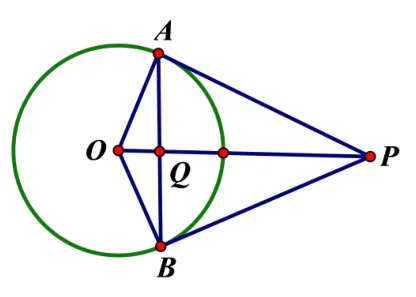
圖1

其實,OP ·OQ=r2?OP ·OQ=OR2(如圖1).給出基圓,可作出P的反演點Q.

(1)若P在基圓⊙O上,則Q就是P.

(2)若P在基圓⊙O外, 自P向反演基圓引切線PA、PB(以OP為直徑的圓與基圓⊙O交于A、B就是切點),連接切點A、B的直線與OP的交點Q為所求.

(3)若P在⊙O內,則反(2)之道以求之.

1.2 反演點的坐標關系

設P(x,y),Q(x′,y′)分別是關于反演變換I(O,r2)的一對反演點,P,Q在過O的同一射線上,所以設x′=λx,y′=λy(λ ＞0),因為|OP|=利用|OP|·|OQ|=r2,可得λ(x2+y2)=r2,所以x′=或者

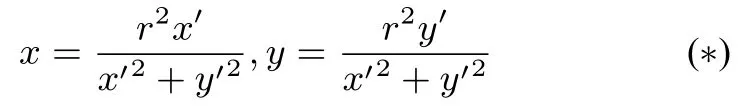
這就是互為反演點P(x,y)與Q(x′,y′)的坐標之間的關系.

如圖1, 我們知道[1]:若⊙O的方程為x2+y2=r2,點P在圓外且坐標為(x0,y0), 則切點連線AB的方程為x0x+y0y=r2.所以AB是點P關于圓O的極線,Q是OP與極線AB的交點.

1.3 反演變換的性質

在反演變換I(O,r2)下, 如果平面π的圖形F變為圖形F′,則稱圖形F′是圖形F關于反演變換I(O,r2)的反形.反演變換的不動點稱為自反點,而反演變換的不變圖形則稱為自反圖形.

對于特殊的直線與圓,可得到其反演性質:

性質1.1反演中心不存在反演點.不共線的兩對反演點共圓.

證明如圖2,設O為反演中心,點A反演點為C,點B的反演點為D.由反演定義得OA·OC=OB·OD=k,故而∠AOB=∠DOC,所以ΔOAB∽ΔODC.由此得∠OAB=∠ODC,所以,點A、C、B、D共圓.證畢.

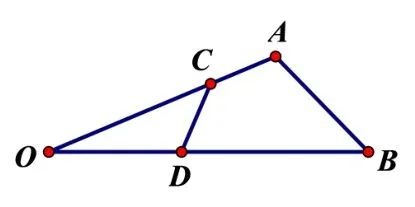
圖2

圖3

說明證明過程中得到的ΔOAB∽ΔODC,∠OBA=∠OCD也是常用結論.

性質1.2反演變換把通過反演中心O的任一條直線變成自身.即通過反演中心的任何直線都是該反演變換下的不變圖形.(直線→直線)

這是顯然的,點、其反演點、反演圓心三點共線.

性質1.3反演變換把任一條不通過反演中心O的直線變成一個通過反演中心O的一個圓,而且這個圓在點O的切線平行于該直線.(直線→圓)

證明設⊙O的方程為= 1,直線l的方程為= 1.如圖3,P(x,y)為l上一點,連OP,與圓交于點R,設點P關于⊙O的反演點為Q(x′,y′).

將反演坐標關系(?)x=代入

這個方程就是點Q的軌跡方程, 表示一個圓, 該圓過坐標系原點O(0,0), 在O點的切線方程為這條切線與直線l平行.

評述直線l:= 1 關于⊙O:= 1 的反演圓方程為相當于已知兩方程中“1=1”代換.

性質1.4反演變換把任一個通過反演中心O的圓變成一個不通過反演中心O的一條直線,而且這條直線平行于該圓的過點O的切線.(圓→直線)

性質1.4 與1.3 互為逆命題.通過反演坐標關系可證明,也可通過平面幾何知識證明,證明略.

性質1.5反演變換把任一個不通過反演中心O的圓變成不能過反演中心O的圓.(圓→圓)自然兩圓的連心線過反演中心O.

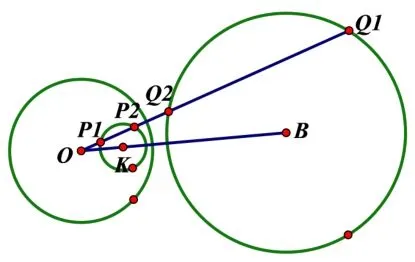
圖4

證明如圖4, 設K為已給的不過反演中心O點的圓, 建立坐標系, 使O為原點,x軸過圓心K(a,0), 在圓K上的點P(x,y)滿足方程(x-a)2+y2=b2或x2+y2-2ax=b2-a2(b ?=a).

這里b是圓K的半徑,設Q是P的反演點,(x′,y′)是點Q的坐標,(x′,y′)和(x,y)在過O的同一射線上.

將反演坐標x=代入圓K方程, 就得出Q(x′,y′)所滿足的方程(b2-a2)(x′2+y′2)+2ar2x′=r4.

當b2-a2?= 0 時, 可變形為x′2+y′2+=

它的軌跡確實是一個不過反演中心的圓.要將圓的反演變換推廣到橢圓中,我們將橢圓看成圓經過伸縮變換而得到,先了解伸縮變換.

2 伸縮變化及其性質

2.1 伸縮變化

高中《數學》選修4-4,1.2 中有曲線的伸縮變換.

定義2設點P(x,y)是平面直角坐標系中的任意一點,在變換φ:的作用下,點P(x,y)對應到點P′(x′,y′),稱φ為平面直角坐標系中的坐標伸縮變換,簡稱伸縮變換.

2.2 伸縮變換的性質

對于伸縮變換很容易得到以下性質:

同素性:在經過伸縮變換之后,點仍然是點,線仍然是線(直線變直線).

結合性:在經過伸縮變換之后,在直線上的點仍然在直線上.

具體還可得到以下不變關系:

(1)直線與圓錐曲線的位置關系不變(相切變相切,相交變相交).

(2)對應圖形的面積比不變.

(3)對應直線的斜率比不變.

(4)兩平行線段或共線線段的比不變(三點共線的比不變),具體如:線段的中點變換后是新線段的中點.

證明較易,略.

3 橢圓的反演變換

3.1 橢圓中的反演變換

圖1 經伸縮變換變為圖5 可得到橢圓中的反演變換.

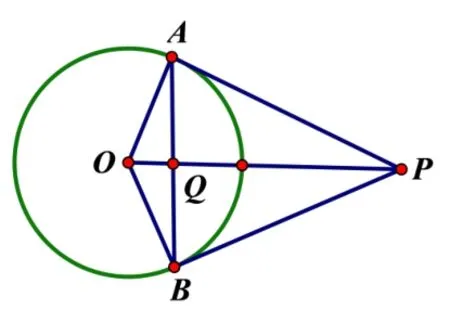
圖1

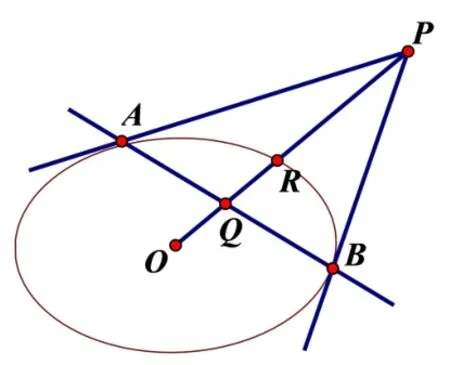
圖5

把橢圓理解為在伸縮變換下的圓,由伸縮變化的的位置關系、線段比例不變性可自然得到橢圓的反演變換.

定義3在平面π上, 橢圓中心為O,線段OP(或延長線)與橢圓相交于點R, 在線段OP上有一點Q滿足條件OP ·OQ=OR2, 我們稱P與Q關于該橢圓互為反演點.(如圖6)

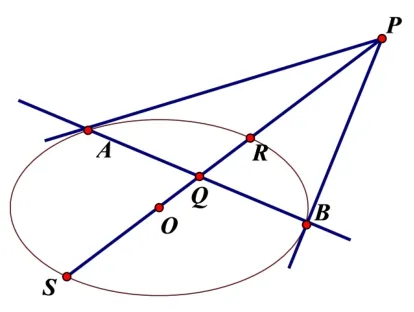
圖6

與圓的反演不同,在圓中OP ·OQ=OR2,OR2=r2是常量.在橢圓中OP ·OQ=OR2,OR2是變量.

由伸縮變換將圖1 變為圖5,或由圓錐曲線的極點與極線知識可知[1],給定橢圓O與不在橢圓上的一點P(如圖6),過點P作橢圓兩條切線,連兩切點A,B,連OP,OP與AB的交點是Q.

進一步可得以下定理:

定理對于橢圓O:= 1 與橢圓外一點P(x0,y0), 若直線OP與橢圓交于S,R(R在P,Q之間),PA,PB是橢圓兩切線.則

(1)兩切點連線AB方程為

(2)Q是線段AB中點.

(4)=-1(調和比).

(以上PA等都是有向線段數量表示)

證明(3)如圖6,即PQ·(PR+PS)=2PR·PS,即(OP-OQ)·(OR-OP+OS-OP)=2(OR - OP)·(OS - OP), 即(OP - OQ)·(-2OP)=2(OR - OP)·(-OR - OP), 即-2(OP2- OQ · OP=-2(OR2-OP2),所以OP ·OQ=OR2?|OP|·|OQ|=|OR|2.

證明(4)

3.2 橢圓反演變換的性質

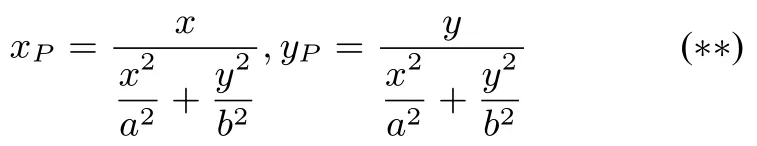
這種反演變換有如下性質:

性質3.1不過反演中心的直線,經反演后,其反形為過反演中心的橢圓(或圓).

證明設直線方程為mx+ny= 1(m2+n2?= 0),反演橢圓為F(x,y)= 1, 由反演變換公式得+=1,變形為mx+ny=F(x,y),(x2+y2?=0),即-mx-ny=0.

性質3.2過反演中心的直線,經反演后,其反形為仍為過反演中心的直線.

證明設直線方程為mx+ny= 1(m2+n2?=0), 反演橢圓為F(x,y)= 1, 由反演變換公式(??)得=0,即mx+ny=0,(m2+n2?=0).所以,結論成立.

性質3.3過反演中心的二次曲線f(x,y)= 0, 經反演后,其反形為經過反演中心三次曲線.特別地,若f(x,y)的二次項可表示為kF(x,y),則其反形為一條直線.(F(x,y)= 1為反演橢圓)

證明設反演橢圓為F(x,y)= 1, 若二次曲線為f(x,y)=Ax2+Bxy+Cy2+Dx+Ey=0,以反演變換公式(??)代入得Ax2+Bxy+Cy2+(Dx+Ey)F(x,y)=0.此為三次曲線.特別地, 若Ax2+Bxy=kF(x,y), 約去F(x,y),得Dx+Ey+k= 0.這是不過反演中心的一條直線.

性質3.4不過反演中心的二次曲線f(x,y)=0,經反演后,其反形為四次曲線.特別地,如f(x,y)= 0 的二次項可表示為kF(x,y),則其象為二次曲線.(F(x,y)=1 為反演橢圓)

證明設反演橢圓為F(x,y)= 1, 若二次曲線為f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+G= 0, 以反演變換公式(??)代入得Ax2+Bxy+Cy2+ (Dx+Ey)F(x,y)+G·F2(x,y)=0.一般的,此為四次曲線.特別地,若Ax2+Bxy+Cy2=kF(x,y),約去F(x,y),上式可化為二次曲線.

可得一般結論:

結論一般地, 若點P的軌跡方程為f(x,y)= 0, 則反演之后的方程為其中x2+y2?=0.

反演變換也可以推廣到雙曲線中,即可推廣到有心二次曲線中.

4 反演變換的應用

例1ΔABC的內切圓與邊BC,CA,AB分別相切于點D,E,F,設L,M,N分別是EF,FD,DE的中點.求證:ΔABC的外心、內心與ΔLMN的外心三點共線.

證明如圖7,設ΔABC的內心為I,內切圓半徑為r.以內心I為反演中心,內切圓為反演圓作反演變換I(I,r2),則A,B,C的反演點分別為L,M,N,因而ΔABC的外接圓反形是ΔLMN的外接圓, 這兩圓的圓心互為一對反演點,連線必過反演中心I.故ΔABC的外心、內心和ΔLMN的外心三點共線.

圖7

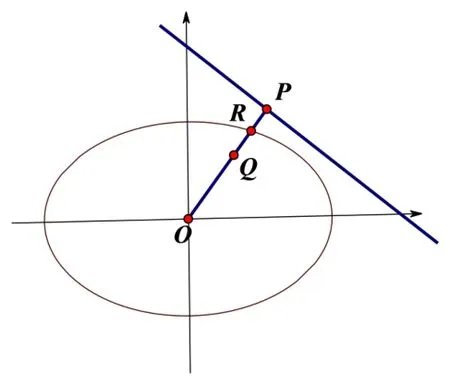
圖8

例2已知橢圓=1,直線=1,P是l上的點,射線OP交橢圓于點R,又點Q在OP上,且滿足|OQ|·|OP|=|OR|2,當點P在l上運動時,求點Q的軌跡.

分析看到|OQ|·|OP|=|OR|2,由性質3.1 可知,點Q的軌跡為

任何問題, 只要向前走一步, 回頭就看得更清楚, 所謂“不識廬山真面目,只緣身在此山中.”由圓的反演變換走向橢圓的反演變換,才能對這個知識體系有深刻的認識.