一類分數(shù)階Kirchhoff型方程Schwarz對稱基態(tài)解的存在性

韓婭玲，向建林

(1.中南財經(jīng)政法大學統(tǒng)計與數(shù)學學院，湖北 武漢430073;2.武漢理工大學數(shù)學系，湖北 武漢430070)

1.引言

本文主要研究如下分數(shù)階Kirchhoff型方程

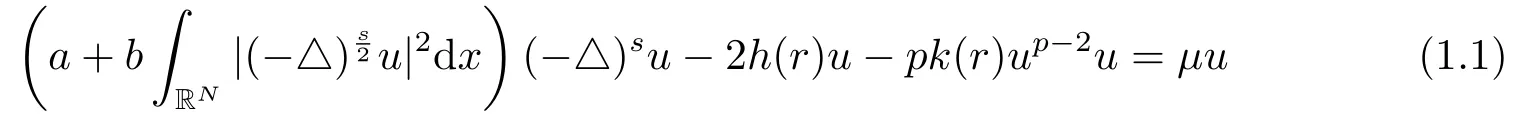
基態(tài)解的存在性，其中常數(shù)a，b ＞0，s ∈(0，1)，μ是拉格朗日常數(shù)，r = |x|，函數(shù)h(r)，k(r)滿足:

(c1) h:(0，∞)→[0，∞)和k :(0，∞)→[0，∞)Lebesgue可測且有界;

(c2) h和k關于r單調(diào)非增.

近年來方程(1.1)受到廣泛關注，特別當s=1時，方程(1.1)表示弦振動中經(jīng)典的Kirchhoff方程，此時方程(1.1)解的存在性及其相關性質(zhì)可見文[1-2]，多重性結果見文[3]，峰解見文[4]，唯一性見文[5]，爆破分析見文[6]等.當0 ＜s ＜1時，文[7]研究了方程(1.1)含臨界指數(shù)情形基態(tài)解的存在性，文[8]探討了方程(1.1)解的多重性.而關于方程(1.1)Schwarz對稱基態(tài)解的存在性，據(jù)我們所知，暫時未見結果.

若b = 0，則方程(1.1)就是通常意義下的分數(shù)階Laplacian方程.近二十年來，分數(shù)階Laplace算子由于在數(shù)學物理和相關領域的廣泛應用，受到非常多數(shù)學研究者的關注，特別是Nezza等在文[9]中得到分數(shù)階Sobolev嵌入不等式后，許多數(shù)學研究者在分數(shù)階Laplacian方程解的存在性，唯一性和非退化性等方面得到了非常豐富的結果[10-15].值得一提的是，利用約束變分理論和常微分方程理論，文[11-12]分別得到了一維和高維情形分數(shù)階Laplacian方程基態(tài)解的存在性和唯一性.文[13]利用約束變分思想和集中緊引理得到了一般的非線性情形分數(shù)階Laplacian方程基態(tài)解的存在性.進一步文[14]證明了一般非線性條件下分數(shù)階Laplacian方程對稱基態(tài)解的存在性，并利用非線性和方程(1.1)非線性相同且滿足條件(c1)和(c2)的情形證明了一般非線性情形時部分條件的最佳性.本文的目的是希望能將文[5，14]的結果推廣到含分數(shù)階的Kirchhoff方程(1.1)中來，進而探討方程(1.1)對稱基態(tài)解的存在性.但是由于非局部項的存在，文[14]中的條件(F5)不能滿足，需要提出新的想法.同時由于非局部項的存在，相應基態(tài)解存在的非線性項指數(shù)范圍更加復雜，需要更細致的估計.

方程(1.1)對應的能量泛函為

由臨界點理論可知方程(1.1)的解就是相應能量泛函I(u)的臨界點.而方程所有解中能量最小的解稱之為方程(1.1)的基態(tài)解，如果解還具有Schwarz對稱性，則稱為Schwarz對稱基態(tài)解.因此討論方程(1.1)Schwarz對稱基態(tài)解的存在性可以轉化為研究如下極小化問題的Schwarz對稱極小解的存在性:

其中

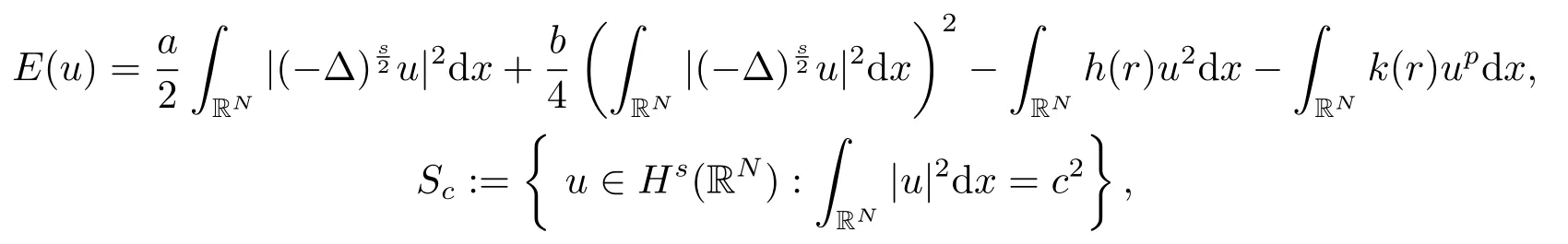
c是常數(shù)，0 ＜s ＜1.Hs(RN)是通常的Besov空間

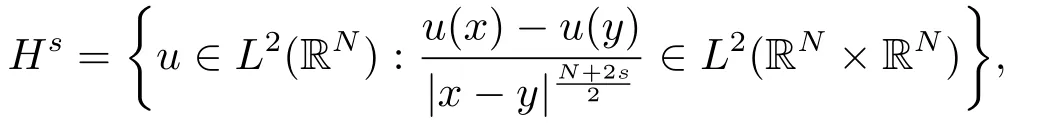
相應范數(shù)為:

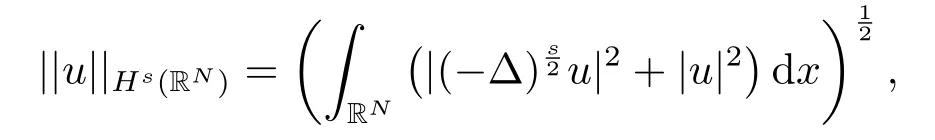
其中

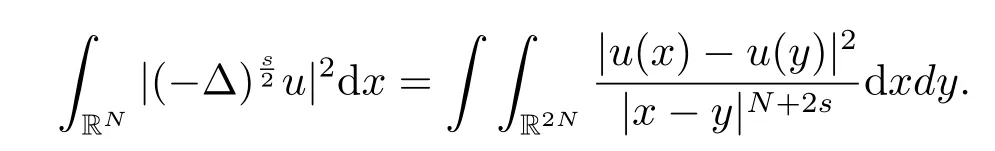
可得到本文的主要結論為:

定理1.1假設函數(shù)h(r)，k(r)滿足條件(c1)和(c2).則

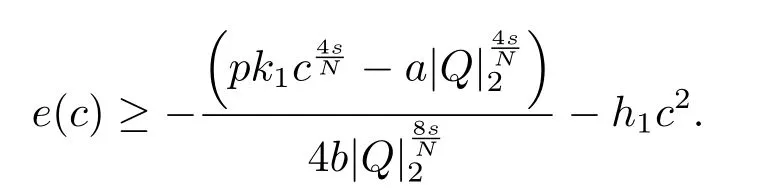
若c ≤c1且h(r)是常值函數(shù)，則極小化問題(1.2)不存在非零極小解.

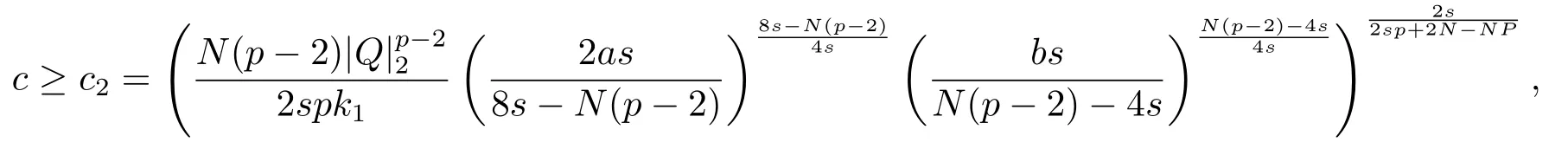
極小化問題(1.2)存在Schwarz對稱極小解，且此時

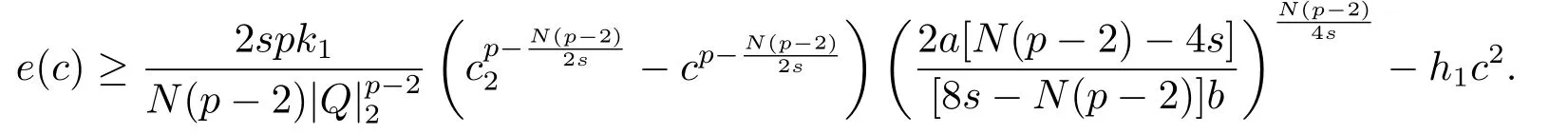
若c ＜c2且h(r)是常值函數(shù)，則極小化問題(1.2)不存在非零極小解.

注假設u ∈Sc使得e(c) = E(u)，由定理可知如果問題(1.2)存在極小解，則能量e(c) ＜0，進一步可知存在一個Lagrange乘子μ，使得方程(1.1)成立，即容易知道極小化問題(1.2)的Schwarz對稱極小解就是方程(1.1)的Schwarz對稱基態(tài)解，且

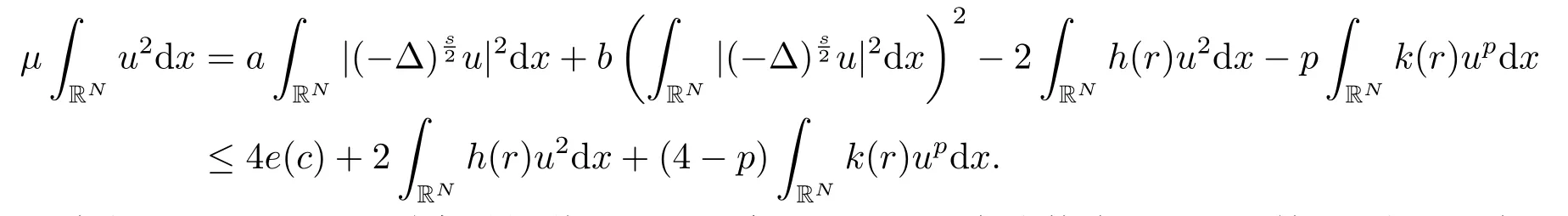
因此當h(r) = 0，p ≥4時容易知道Lagrange乘子μ ＜0.而在分數(shù)階Laplacian情形，由于沒有非局部項，會簡單一些.

2.準備工作

在證明本文定理前，先介紹如下分數(shù)階Gagliardo-Nirenberg不等式[12]

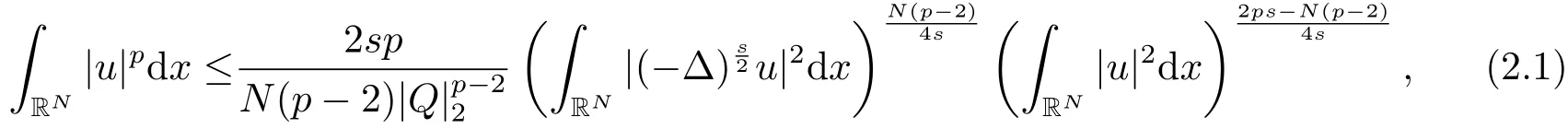
上述等式成立當且僅當u(x)是函數(shù)Q(x)的伸縮平移，其中Q(x)是下述非線性分數(shù)階方程唯一徑向?qū)ΨQ正解:

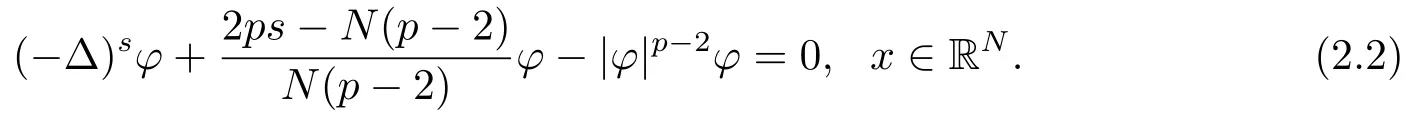
由方程(2.2)和Pohozaev恒等式有

引理2.1對任意的θ ＞1，有e(θc)≤θ2e(c).

證對任意θ ＞1，設uθ(x)=u(θ

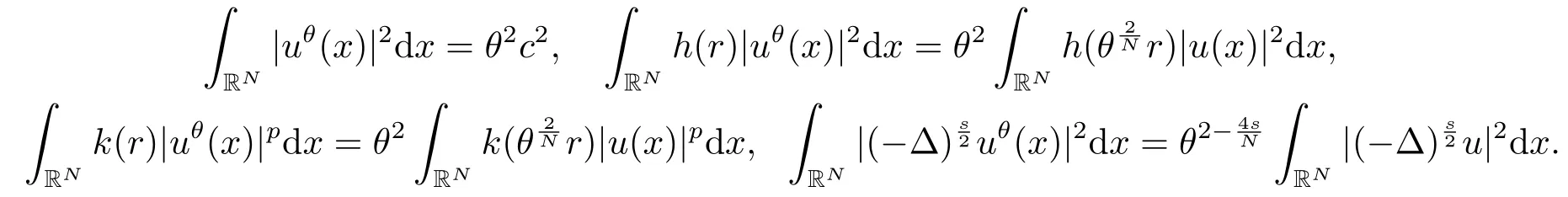
因此，由條件(c2)可得

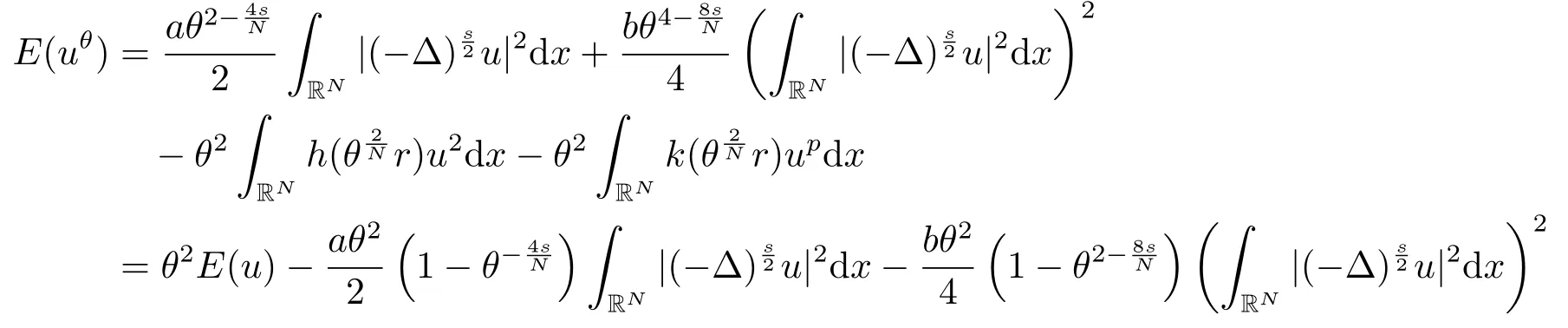
這意味著對任意的θ ＞1，有

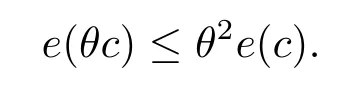
引理2.2假設{un}是一列Schwarz對稱的極小化序列，如果在Hs(RN)上un?u，則E(u)≤lim infn→∞E(un).

證由文[9]可知，范數(shù)||u||Hs具有弱下半連續(xù)性

進一步可得

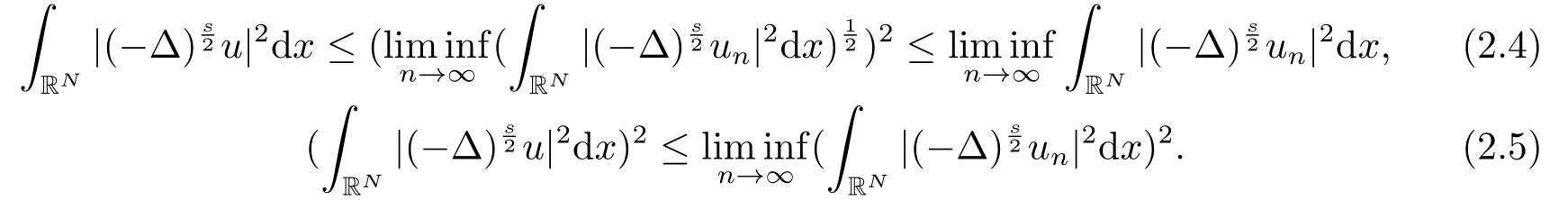
設R ＞0是一個常數(shù)，記BR(0)={x ∈RN:|x|≤R}，則

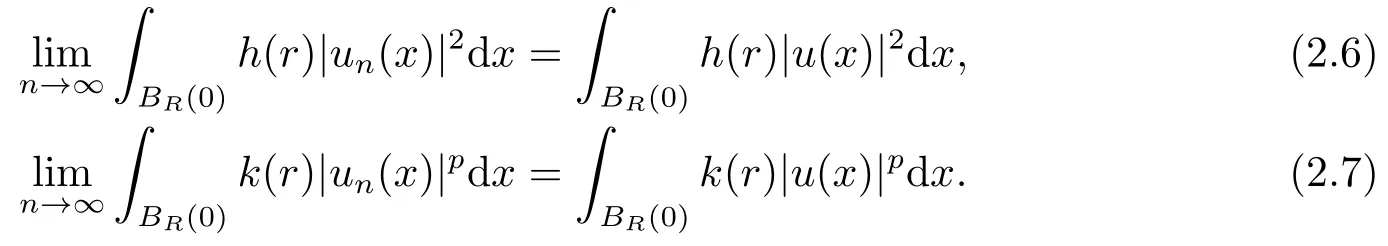
一方面，由函數(shù)h(r)，k(r)的有界性，存在h1，k1，使得

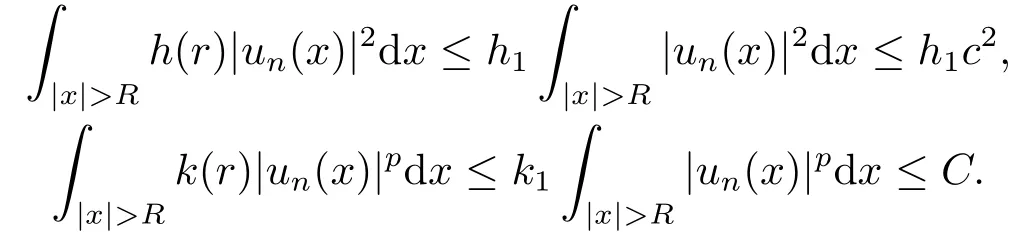
另一方面，由條件(c2)，不妨設limr→∞h(r) = h(∞) = 0 = k(∞) = limr→∞k(r)，綜合上述各式，可得

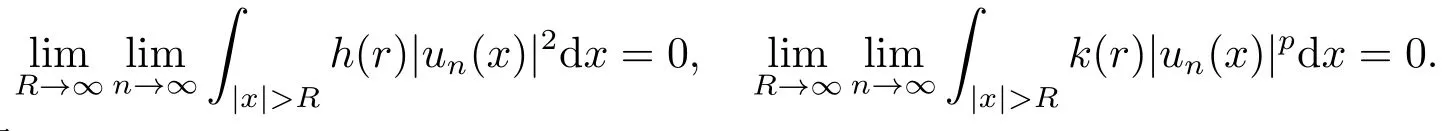
同理可得

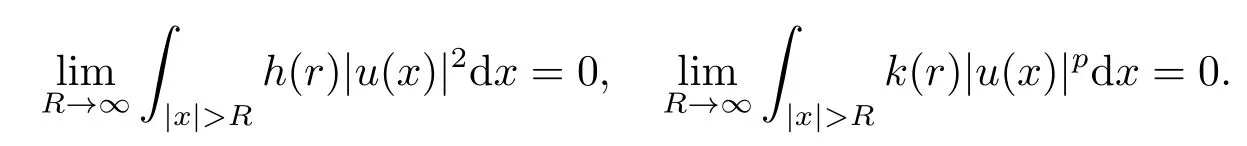
上述兩式結合(2.6)和(2.7)可得

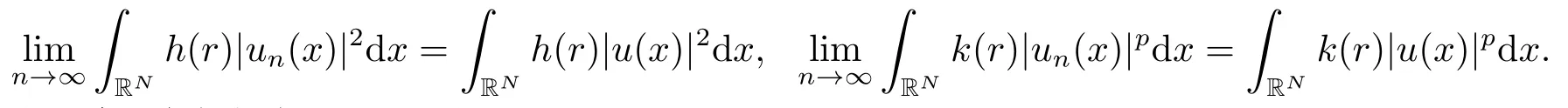
進一步，結合上式和(2.5)可知

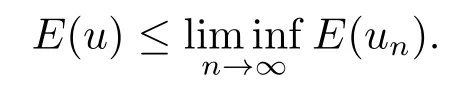
引理2.3假設函數(shù)其中t ＞0，則

證由函數(shù)gp(t)的定義易知gp(0)=-h1c2.

當c ＞c1時，通過計算(t)=0可得函數(shù)gp(t)在(0，+∞)上有唯一極小值點為

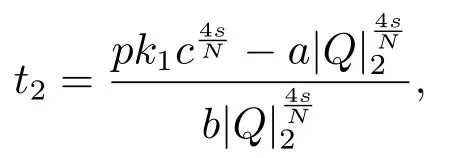
進一步可得函數(shù)gp(t)在(0，+∞)上取得極小值

進一步可知當t →∞時gp(t)→-∞，因此gp(t) 無法達到極小值.

引理2.4假設函數(shù)h(r)，k(r)滿足條件(c1)和(c2)，則

證對任意的u ∈Sc，利用Gagliardo-Nirenberg不等式，可得

對任意的u ∈Sc，做伸縮可得

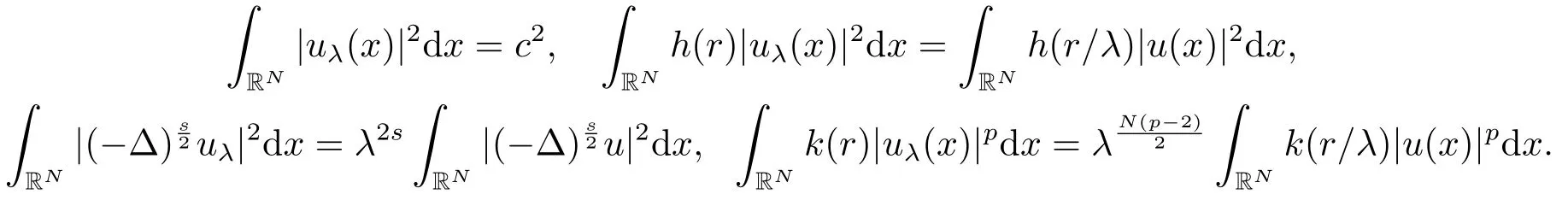
因此有

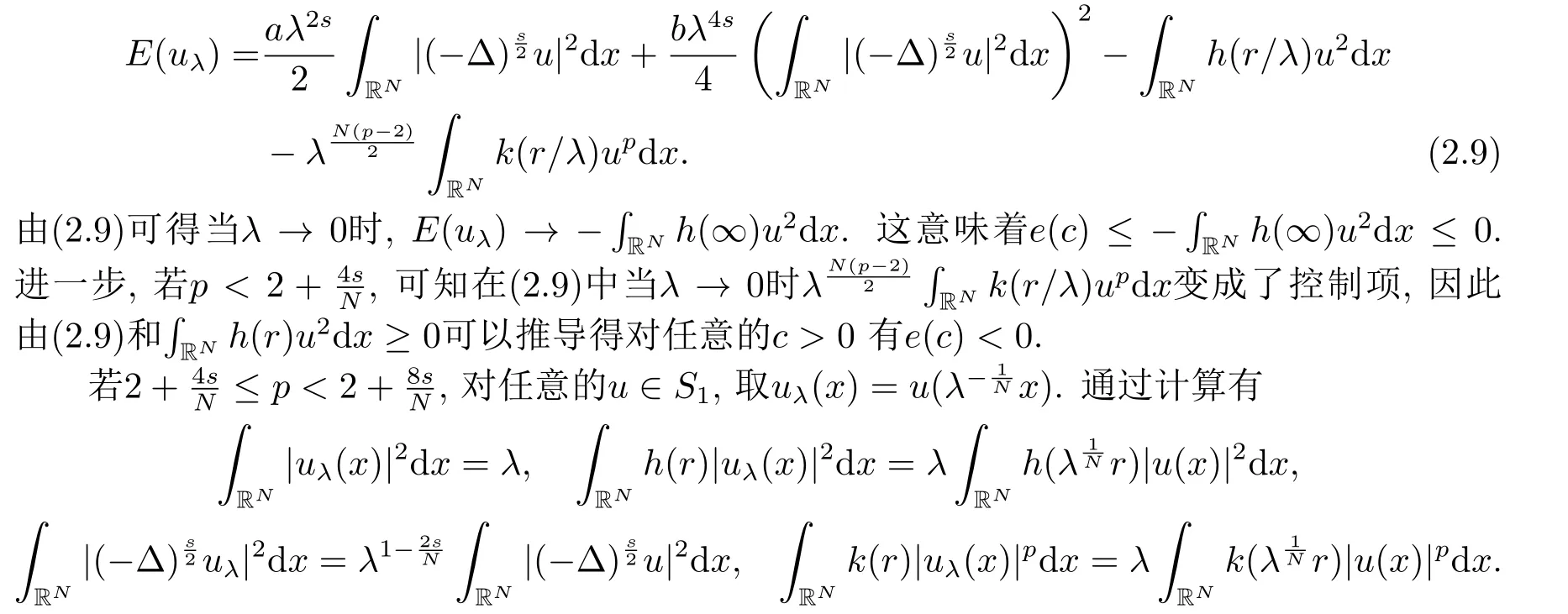
由上述等式，可得

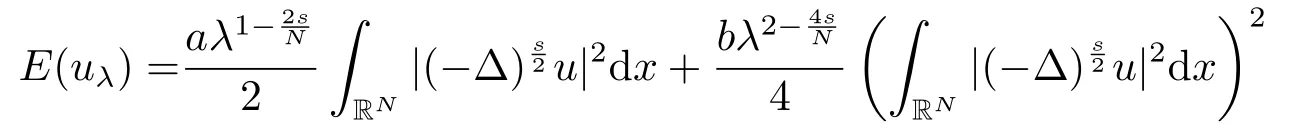
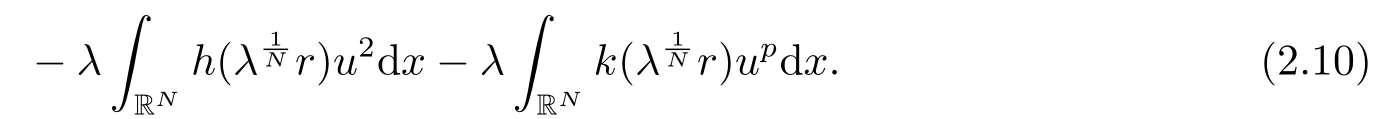
3.定理證明

定理1.1的證明1) 當2 ＜p ＜2+時: 由引理2.3中(i)知，對?c ＞0，gp(t) ≥gp(t1)，因此e(c) ≥gp(t) ≥gp(t1)，即e(c) ＞-∞.對任意的u ∈Hs(RN)，易知|u| ∈Hs(RN)且E(|u|) =E(u).由文[16] 中定理A.1可知當0 ＜s ＜1時關于dx的嚴格重排不等式成立.設{un}是極小化問題(1.2)的一個極小化序列，表示un的對稱遞減重排，則滿足

(i) 對任意x ∈RN，≥0;

(iii) 對任意的r ∈[1，∞)，若un∈Lr，則||r=|un|r;

(iv) 若un∈Hs(RN)，則

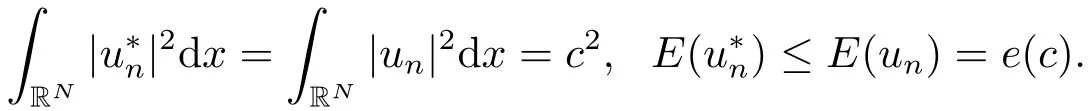
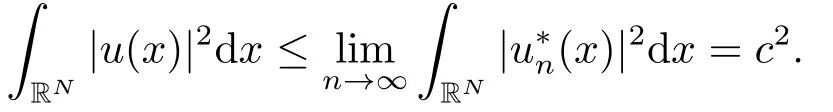
利用引理2.2可得

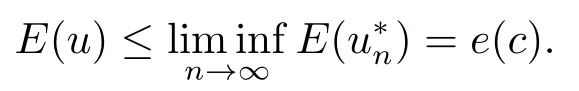
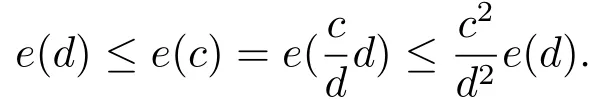
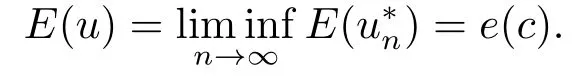
因此極小化問題(1.2)存在正的極小解u.設u*是正極小解u的對稱遞減重排，相似文[17]中定理1可得

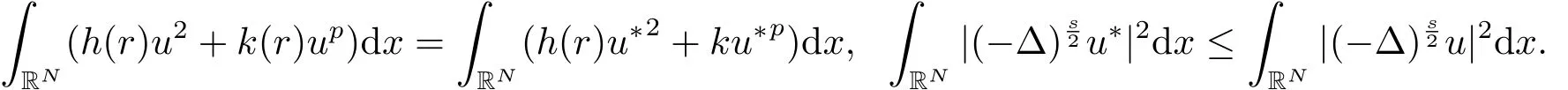
經(jīng)過簡單的計算即得E(u*)≤E(u).因此極小化問題(1.2)的解u是Schwarz對稱的.進一步，由引理2.3中(i)可知此時的極小值e(c)≥gp(t1).

若c ≤c1，由引理2.3中(ii)知e(c) ≥gp(t) ≥-h1c2.令其中λ是一個常數(shù)，Q(x)是(2.2)的非負徑向解，因此即uλ(x) ∈Sc.通過計算，利用(2.3)，可得

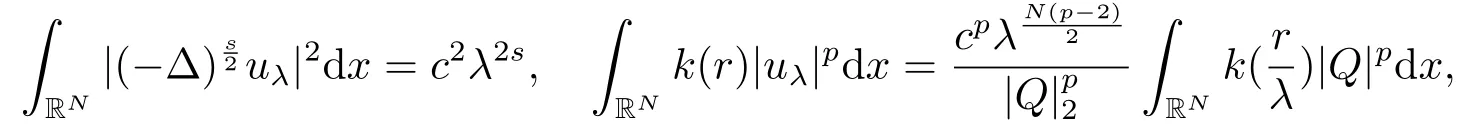
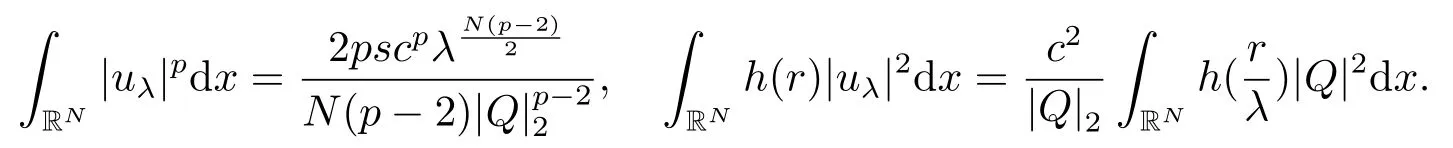
因此當λ →0+時，

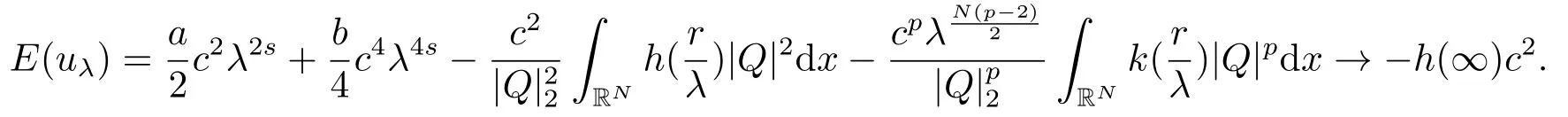
因此只有當h1= h(∞)，即h(r)是常數(shù)時才能證明當c ≤c1時極小化問題(1.2)不存在非零極小解.

若c ＜c2，結合引理2.3(iii)，相似上面情形2)c ≤c1時的證明可得當c ＜c2時只有當h1=h(∞)，即h(r)是常數(shù)時才能證明極小化問題(1.2)不存在非零極小解.

當c ＞c3時，由引理2.3中(iv)知e(c) ≥-∞; 令其中λ是一個常數(shù)，Q(x)是(2.2)的非負徑向解，當λ →+∞時可得

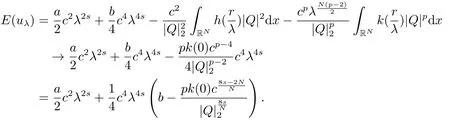
因此當k(0)=k1時，E(uλ)→-∞，即k(r)是常數(shù)時對所有的c ＞c3，極小化問題(1.2)不存在極小解.

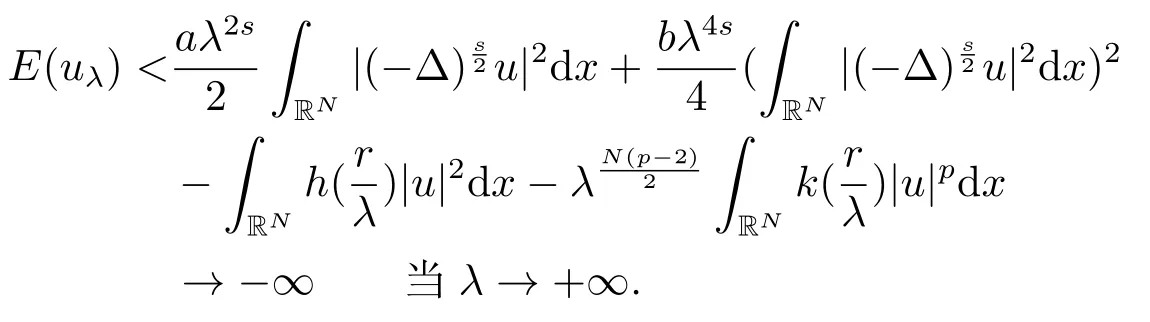
即對所有的c，e(c) = -∞，這意味著當p ＞2+時極小化問題(1.2)不存在Schwarz對稱極小解.