一類奇異攝動對流擴散方程組的自適應(yīng)網(wǎng)格方法的收斂性分析

包小兵，方虹淋，劉利斌

(1.池州學院大數(shù)據(jù)與人工智能學院，安徽 池州247000; 2.重慶工程學院通識學院，重慶400900; 3.南寧師范大學數(shù)學與統(tǒng)計學院，廣西 南寧530023)

1.引言

本文考慮如下弱耦合的奇異攝動對流擴散方程組：

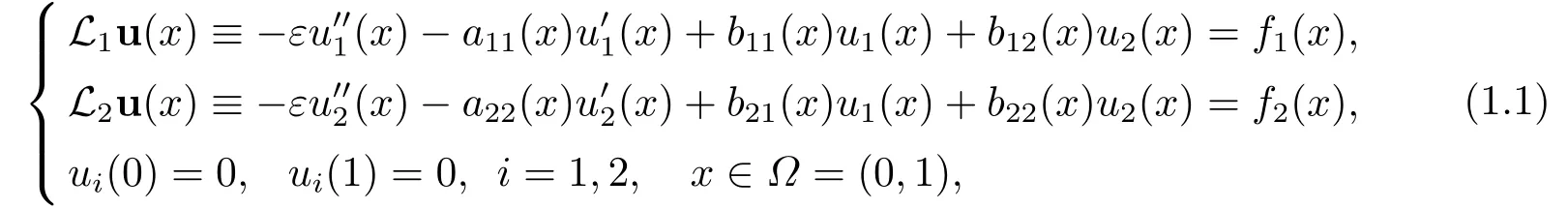
其中0 ＜ε ?1是攝動參數(shù)，u(x)=(u1(x)，u2(x))T，函數(shù)aii(x)，bij(x)和fj(x)，i，j =1，2，為足夠光滑的函數(shù).假設(shè)存在常數(shù)α，α*，η，使得

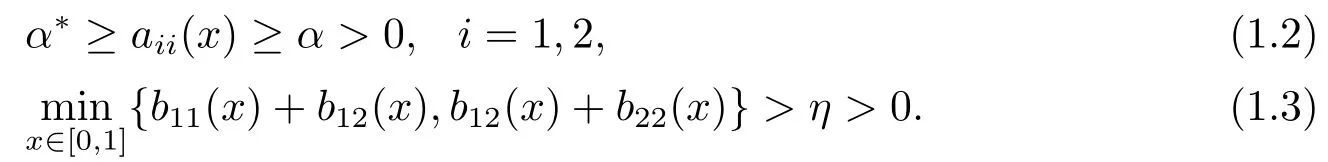
基于假設(shè)條件(1.2)-(1.3)，問題(1.1)存在唯一解，且當ε →0時，在x = 0點存在寬度為O(ε|ln ε|)的邊界層.[1]

眾所周知，奇異攝動問題來源于工程和應(yīng)用數(shù)學的許多分支，例如流體力學、熱傳導(dǎo)、半導(dǎo)體和化學反應(yīng)等.[2]一般而言，這類問題所對應(yīng)的微分方程的高階導(dǎo)數(shù)項包含小的攝動參數(shù)，從而導(dǎo)致很難求出其精確解，尤其是非線性的問題.因此，研究這類問題的有效的數(shù)值方法顯得非常重要.

一直以來，單個奇異攝動對流擴散方程的數(shù)值方法備受許多學者的關(guān)注.[3]近年來，奇異攝動對流擴散方程組的層適應(yīng)網(wǎng)格方法逐漸引起了學者們的興趣.CEN在文[1]中考慮了問題(1.1)的Shishkin網(wǎng)格方法，并證明了數(shù)值方法是幾乎一階一致收斂的.Roos和Reibiger[4]考慮了具有單個攝動參數(shù)ε 的奇異攝動對流擴散方程組，證明線性有限元方法在Shishkin網(wǎng)格上是幾乎二階收斂的.作者在文[5]中討論了奇異攝動對流擴散方程組(1.1)的有限差分格式，并在Shishkin網(wǎng)格上證明了數(shù)值方法是幾乎一階收斂的.針對奇異攝動對流擴散方程組，LIN?[6]在任意網(wǎng)格上構(gòu)造了一個迎風有限差分格式，并分別在Shishkin網(wǎng)格和Bakhvalov網(wǎng)格上證明了數(shù)值方法的收斂階是O(N-1ln N)和O(N-1) ，其中N表示網(wǎng)格區(qū)間的個數(shù).O’Riordan和Stynes[7]討論了一類強耦合的奇異攝動對流擴散方程組有限差分方法，并在Shishkin網(wǎng)格上給出了數(shù)值方法的收斂性.Kumar等[8]討論了一類奇異攝動對流擴散方程組的Shishkin網(wǎng)格方法，并給出了相應(yīng)的收斂性分析.

在奇異攝動問題的層適應(yīng)網(wǎng)格方法受到廣泛關(guān)注的同時，奇異攝動對流擴散方程的自適應(yīng)網(wǎng)格算法越來越受到許多學者的青睞[9-14].而關(guān)于奇異攝動對流擴散方程組的自適應(yīng)網(wǎng)格算法，可參見德國學者Lin?在2009年發(fā)表的文[15].接著，LIU和CHEN在文[16-17]中分別討論了一類弱耦合和強耦合的奇異攝動對流擴散方程組的自適應(yīng)網(wǎng)格算法，利用多項式插值技術(shù)，給出了離散格式的最大范數(shù)的后驗誤差估計，并以此構(gòu)造了一個類似于弧長的網(wǎng)格控制函數(shù)及相應(yīng)的網(wǎng)格生成算法.MAO和LIU[18]針對一般的強耦合的奇異攝動對流擴散方程組，構(gòu)造了迎風有限差分格式的后驗誤差估計和相應(yīng)的網(wǎng)格生成算法.值得一提的是文[15-18]所提出的奇異攝動對流擴散方程組的自適應(yīng)網(wǎng)格算法都是基于后驗誤差估計和網(wǎng)格等分布原理.如文[10]所述，這種算法屬于全離散的自適應(yīng)網(wǎng)格算法.在文[10，13，19-20]中，基于精確的弧長控制函數(shù)和網(wǎng)格等分布原理，作者研究了單個奇異攝動對流擴散方程的半離散的自適應(yīng)網(wǎng)格算法，并給出了算法的先驗誤差估計和收斂性分析.因此，本文將在此基礎(chǔ)上，系統(tǒng)分析奇異攝動對流擴散方程組(1.1)的自適應(yīng)網(wǎng)格算法的收斂性.首先，基于標準的迎風差分格式，給出相應(yīng)的局部截斷誤差.然后，利用包含方程精確解的網(wǎng)格控制函數(shù)、網(wǎng)格等分布原理和精確解的穩(wěn)定性估計，證明了半離散格式的自適應(yīng)網(wǎng)格算法是一階收斂的.最后的數(shù)值試驗進一步驗證了本文的理論結(jié)果.

注1.1本文中的C表示與攝動參數(shù)ε以及網(wǎng)格參數(shù)N無關(guān)的正常數(shù)，且在不同地方取值不同.對于單個函數(shù)v(x)，x ∈= [0，1]，定義最大范數(shù)對于向量函數(shù)v(x)=(v1(x)，v2(x))T，定義‖v(x)‖=max{‖v1(x)‖，‖v2(x)‖}，‖v(xi)‖=max{|v1(xi)|，|v2(xi)|}，i=0，1··· ，N.另外，為了方便，對于任意函數(shù)g(x)，記gi=g(xi).

2.預(yù)備知識

在這部分，為了證明問題(1.1)的數(shù)值解的誤差估計，我們首先列出極大值原理和問題(1.1)的解的穩(wěn)定性.

引理2.1(極大值原理)[1]假設(shè)v(x) 是一個光滑的函數(shù)，如果對于任意的x ∈Ω，滿足不等式v(0)≥0，v(1)≥0以及L1v ≥0，L2v ≥0，則有v(x)≥0成立.

基于引理2.1中的極大值原理，可進一步得到問題(1.1)的解滿足如下穩(wěn)定性結(jié)果:

引理2.2(穩(wěn)定性)[1]基于假設(shè)條件(1.2)-(1.3)，方程組(1.1)的精確解u(x)存在如下穩(wěn)定性估計:

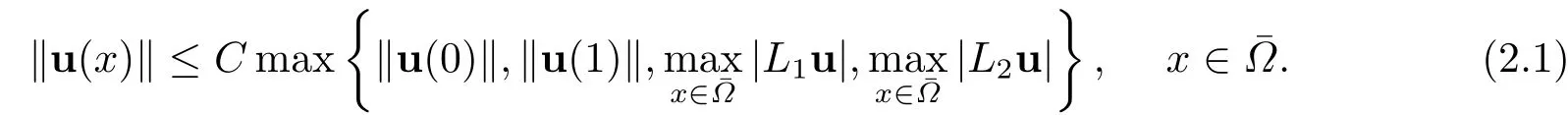
進一步，由文[1]的引理3和引理4，可得如下引理:

引理2.3方程組(1.1)的精確解u(x)的k(k =1，2)階導(dǎo)數(shù)滿足如下估計:

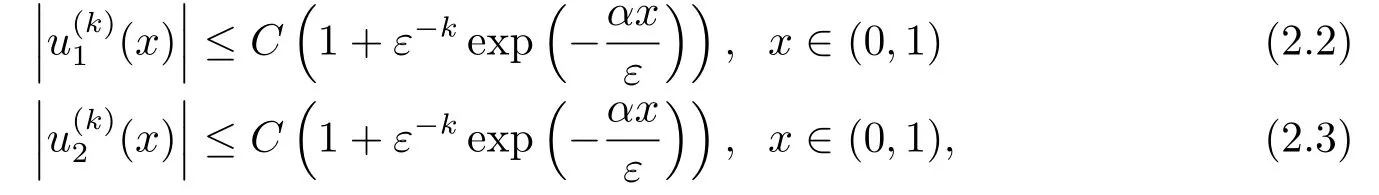
3.離散問題和非均勻網(wǎng)格

為了構(gòu)造問題(1.1)的離散格式，將區(qū)間[0，1]分成N個小區(qū)間，即可構(gòu)造如下的非均勻網(wǎng)格:

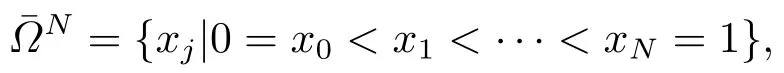
其中網(wǎng)格步長hj=xj-xj-1，則在任意非均勻網(wǎng)格N下，問題(1.1)的迎風有限差分格式為:

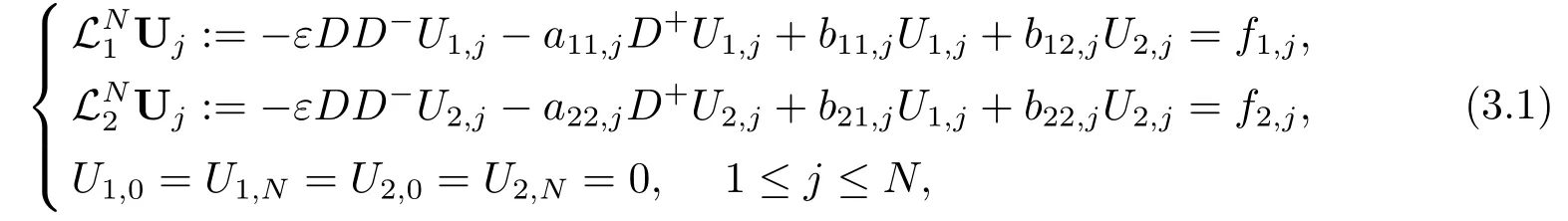
其中Uj=(U1，j，U2，j)T為u(xj)=(u1(xj)，u2(xj))T的近似值，且差分算子定義如下:

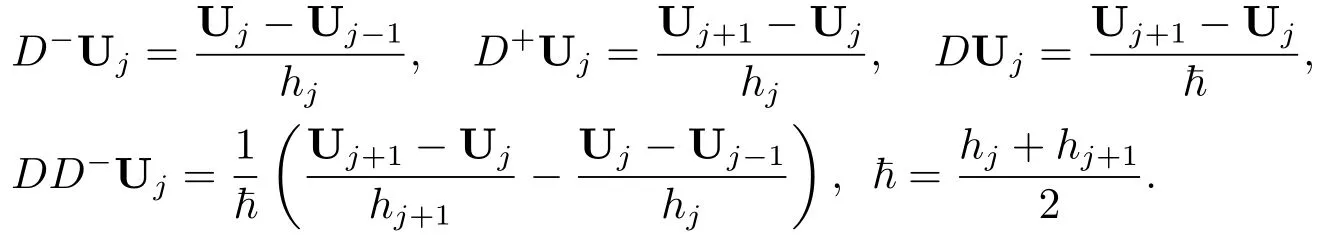
對任意的非均勻網(wǎng)格ΩN，如果存在非負函數(shù)M(·，x)，使得

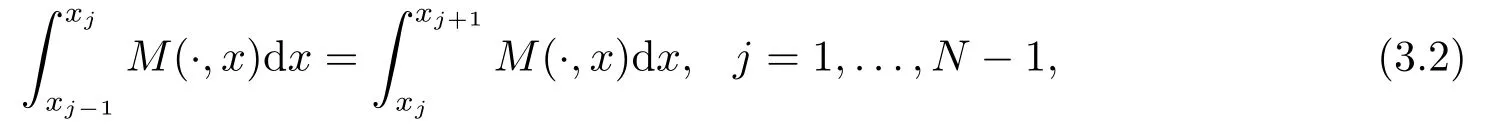
則稱此非均勻網(wǎng)格ΩN是等分布的，且M(·，x)稱為控制函數(shù).進一步，(3.2)可寫為:

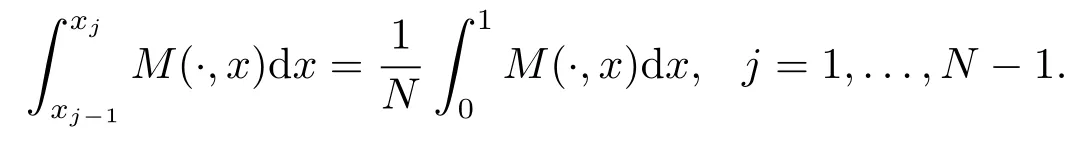
一般情況下，對于單個奇異攝動微分方程，最常用的控制函數(shù)為弧長函數(shù)M(u(x)，x) =其中u(x)是單奇異攝動問題的精確解.最近，LIU和CHEN[16]以及MAO和LIU[18]構(gòu)造了奇異攝動對流擴散方程組的自適應(yīng)網(wǎng)格算法，他們構(gòu)造了如下的控制函數(shù):

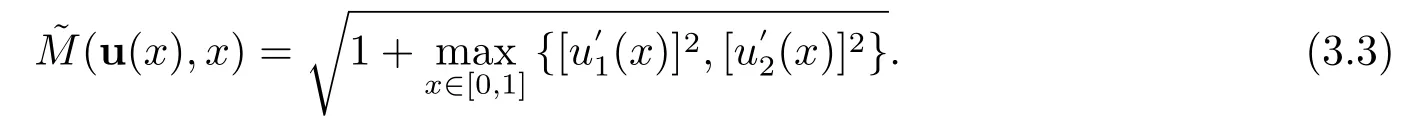
本文也將選取~M(u(x)，x) 作為控制函數(shù)來構(gòu)造自適應(yīng)網(wǎng)格，即由(3.2)可得，

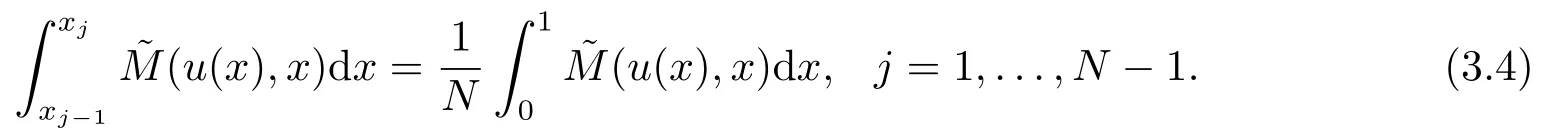
對于任意的ξ ∈(0，1)，構(gòu)造映射x=x(ξ)∈(0，1)，則有:

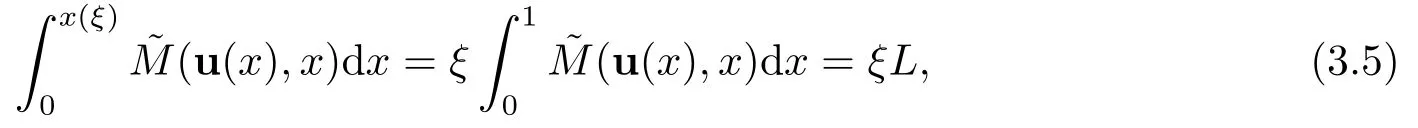
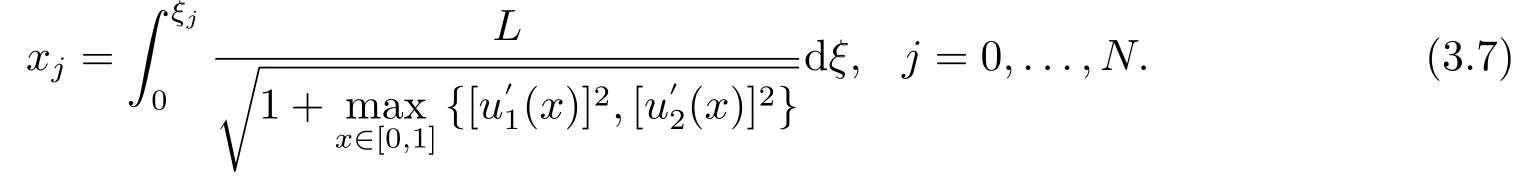
因此，網(wǎng)格步長為:

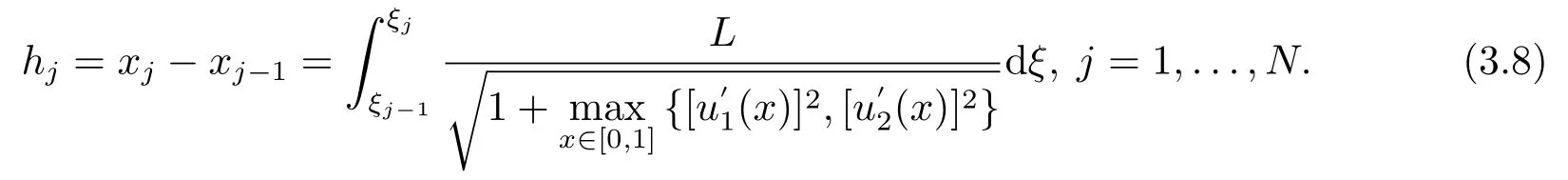
引理3.1對于滿足等分布原理(3.4)的任意一個網(wǎng)格有

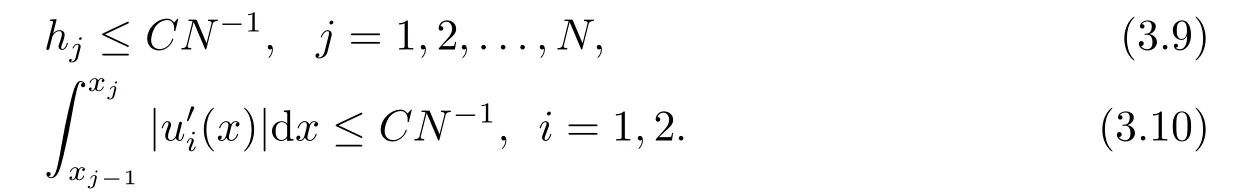
證對于任意的x ∈(0，1)，由引理2.3可以得到弧長

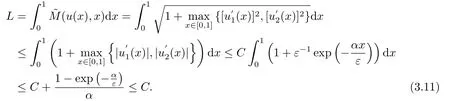
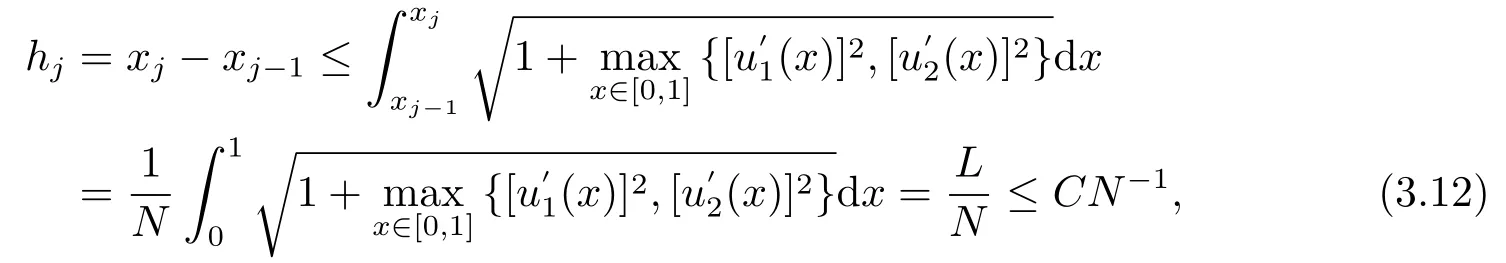
即可得到(3.9)式.

進一步，由(3.6)，(3.11)和(3.12)可得

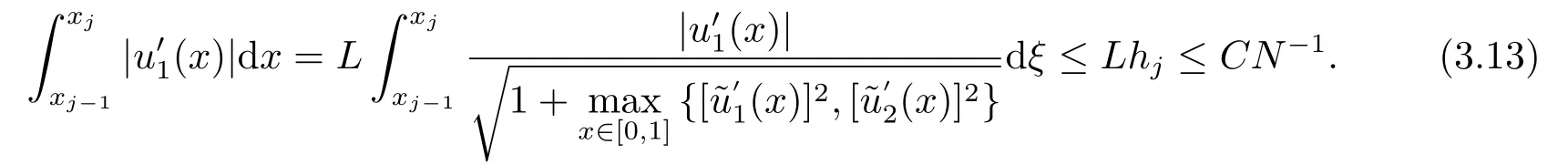
類似地，還可得到:

即完成(3.10)的證明.

4.收斂性分析

顯然，離散格式(3.1)在點xj的局部截斷誤差分別為:

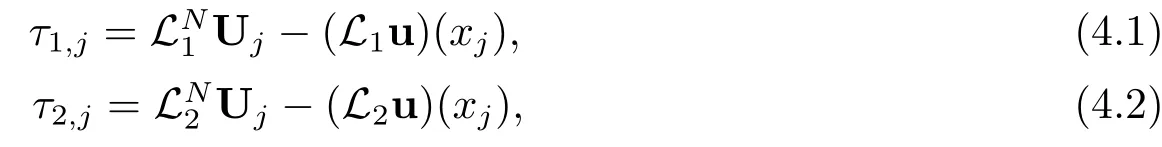
其中u和Uj分別表示方程組(1.1)和離散格式(3.1)的解.

為了給出截斷誤差的具體表達式，我們首先給出下列引理:

引理4.1[18]對于任意的函數(shù)ψ(x)∈?3(，有:

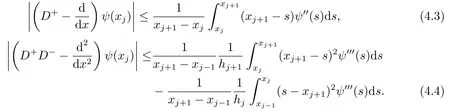
引理4.2設(shè)差分格式(3.1)在點xi的局部截斷誤差為τi，j，則有:

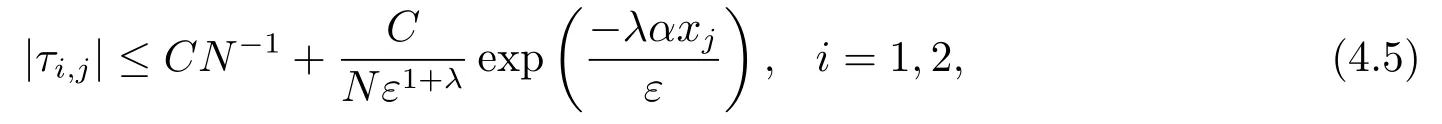
其中C為與參數(shù)ε無關(guān)的正常數(shù)，0 ＜λ ＜1.

證首先，當i=1時，由泰勒展開可得

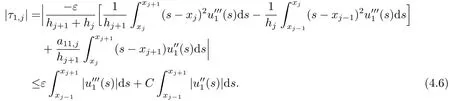
對(1.1)的第一個方程求導(dǎo)，并由(4.6)式和引理3.1可得

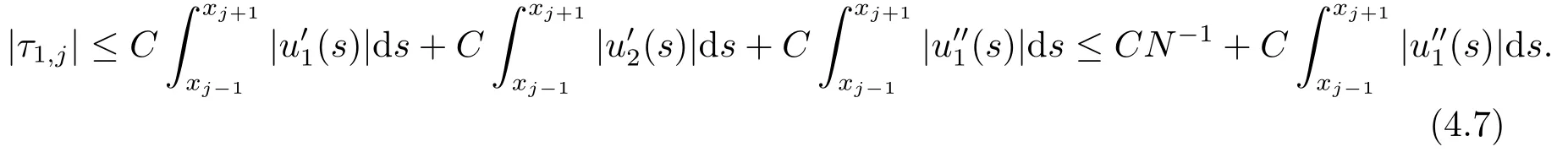
進一步，由(3.7)和(3.11)，可得

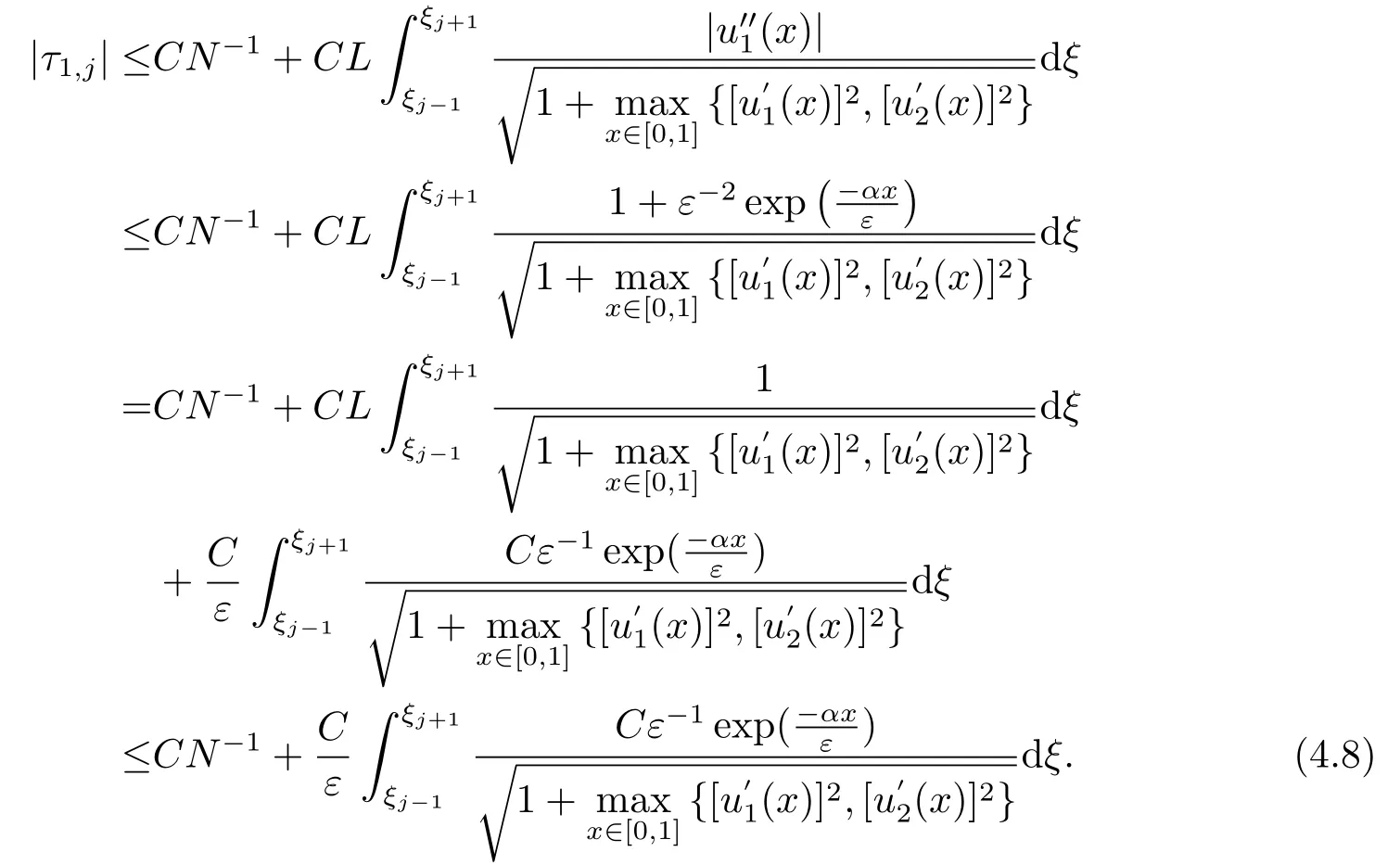
再由引理2.3可得

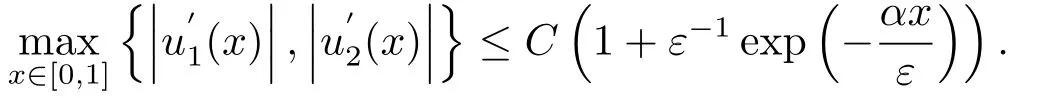
則顯然有，

與文[10]的引理5.1類似，存在常數(shù)C1和C2，使得:

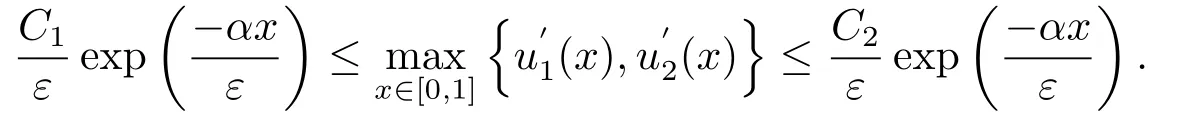
進一步由(4.8)可得

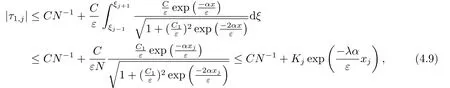
其中0 ＜λ ＜1是與ε，N無關(guān)的，并且

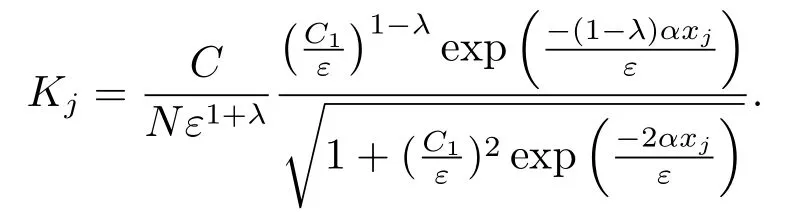
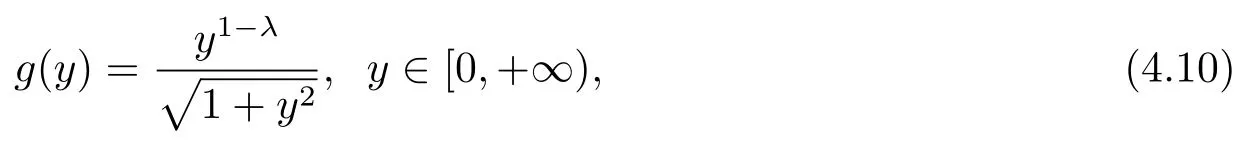
顯然，g(y)是區(qū)間[0，y*]上的增函數(shù)，其中由0 ＜λ ＜1，易知g(y*)≤C，進一步有

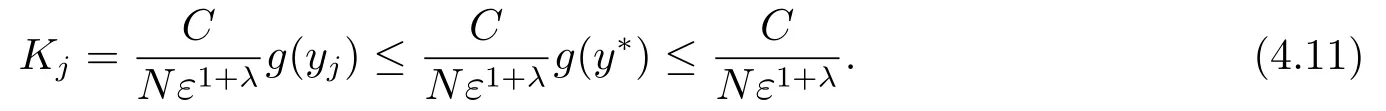
類似地，當i=2時，可以得到:

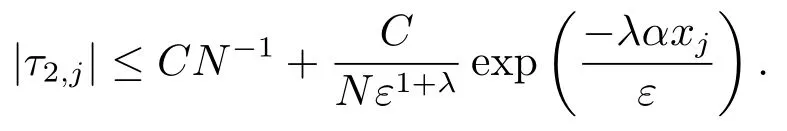
下面為了討論數(shù)值解的誤差估計，首先給出網(wǎng)格函數(shù)的性質(zhì).

引理4.3定義網(wǎng)格函數(shù)Sj=(S1，j，S2，j)T滿足

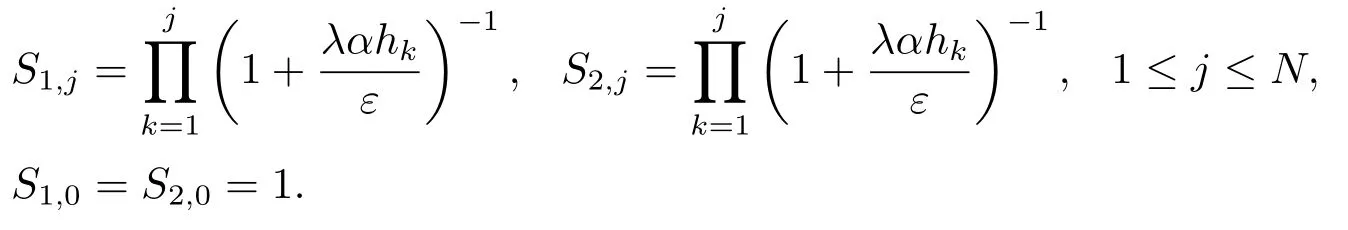
則對于j =1，2，...，N -1，存在一個常數(shù)C，使得

證該引理的證明類似于文[19]引理4.4的證明.當i=1時，定義

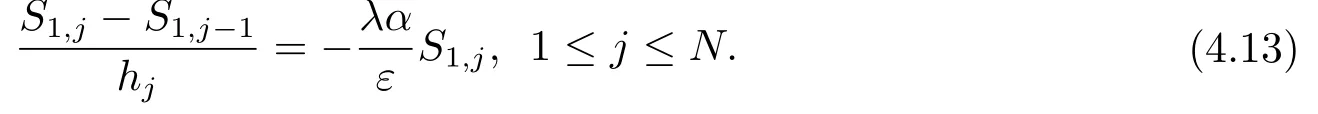
結(jié)合式(3.1)和(4.13)可得到

由于hj+1/?j≤2，則有

當i=2時，同理可證得

下面的引理給出了網(wǎng)格函數(shù)Sj的上下界.

引理4.4[19]網(wǎng)格函數(shù)滿足

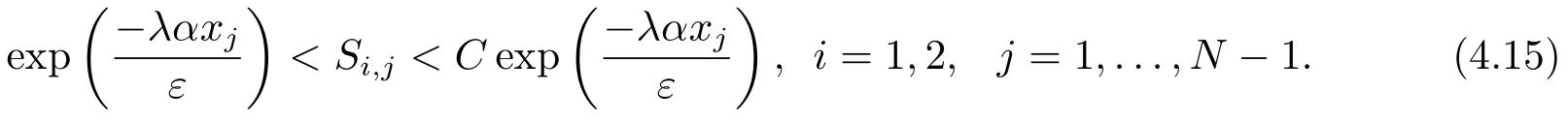
定理4.1令u(x)是方程(1.1)的解，Uj(x)是離散格式(3.1)的解，則

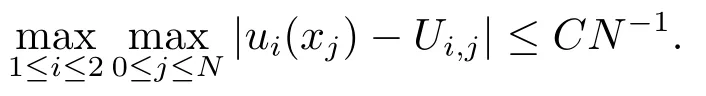
證令ej=(e1，j，e2，j)T=|u(xj)-Uj|為數(shù)值解Uj在x=xj(j =0，1，··· ，N)點的絕對誤差，則由截斷誤差τi，j與ei，j的關(guān)系可得

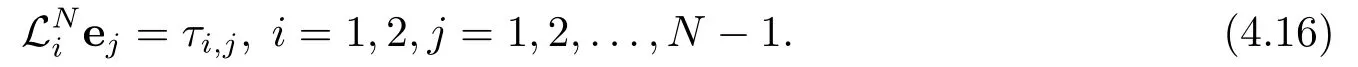
進一步，由引理4.2-4.4，有

由于e0=eN=0，再由引理3.1和比較原理(見文[10]的引理5.3)可得

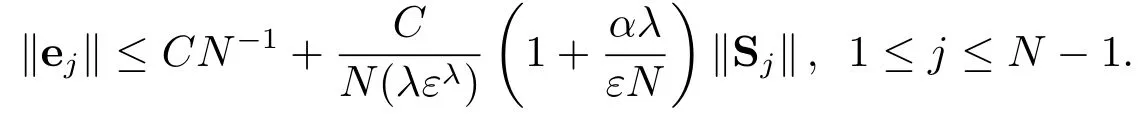
由引理4.3中Sj的定義，有

設(shè)攝動參數(shù)取值為ε=10-a，其中a是一個正數(shù)，選擇λ=1/m0，這里m0=max{4，a}，則

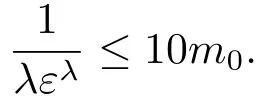
故可以得到‖ej‖≤CN-1，即可完成該定理的證明.

5.數(shù)值實驗與結(jié)果分析

考慮到(3.3)中的網(wǎng)格控制函數(shù)包含方程(1.1)的精確解，在實際計算過程中，我們常常構(gòu)造近似的網(wǎng)格控制函數(shù)來代替(3.3).在這一小節(jié)，為了驗證本文關(guān)于自適應(yīng)網(wǎng)格算法的理論結(jié)果，我們將采用文[16，17]中的網(wǎng)格迭代算法來生成相應(yīng)的自適應(yīng)網(wǎng)格(在這里，網(wǎng)格終止條件C0=1.3)，并考慮如下奇異攝動對流擴散方程組

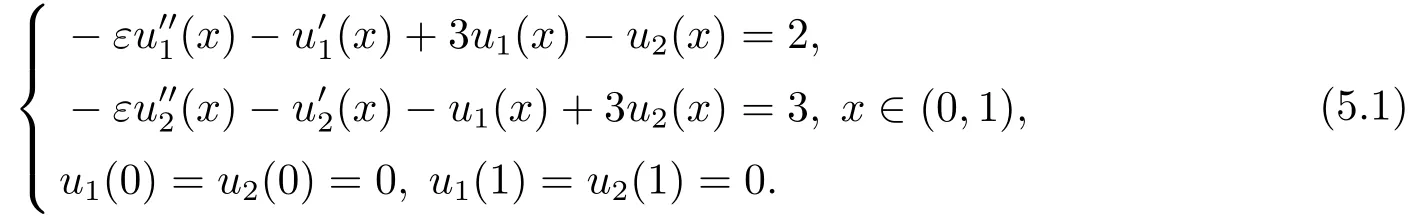
由于該問題的精確解沒有給出，我們采用如下公式來計算數(shù)值解的絕對誤差

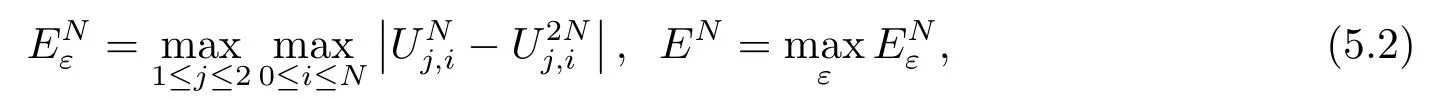
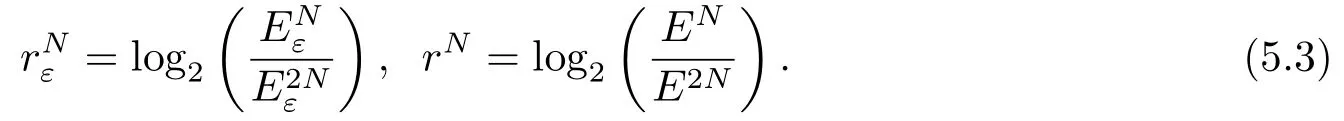
當ε=10-2k，k =0，1，··· ，5，N =2j，j =6，7，··· ，12時，表1中列出了自適應(yīng)網(wǎng)格算法計算得到的數(shù)值結(jié)果，其中每一個ε所對應(yīng)的第三行表示網(wǎng)格生成算法的迭代次數(shù).顯然，對于每一個ε，隨著N的逐漸增大，本文自適應(yīng)網(wǎng)格算法的收斂階逐步達到一階.對于足夠小的ε，網(wǎng)格生成算法的迭代次數(shù)也不大，且不隨N的增大而增加.當ε=10-5，N =2j，j =6，7，··· ，12時，表2分別列出了迎風有限差分格式(3.1)在均勻網(wǎng)格、Shishkin網(wǎng)格和自適應(yīng)網(wǎng)格上的誤差和收斂階，其中Shishkin網(wǎng)格的構(gòu)造見文[1].從表2的數(shù)值結(jié)果可以看出，本文的自適應(yīng)網(wǎng)格方法的收斂階明顯比均勻網(wǎng)格和Shishkin網(wǎng)格的收斂階要高一些，進一步驗證了理論結(jié)果.

另外，為了進一步的讓讀者了解自適應(yīng)網(wǎng)格生成算法的迭代過程，當ε=10-7，N =64時，從下往上看，圖1畫出了每迭代一次，網(wǎng)格的移動過程.同時，圖2給出了問題(5.1)的數(shù)值解的變化曲線圖.顯然，由圖1-2可以看出，問題(5.1)的解在x=0點存在邊界層.

表1 本文自適應(yīng)網(wǎng)格方法計算得到的數(shù)值結(jié)果

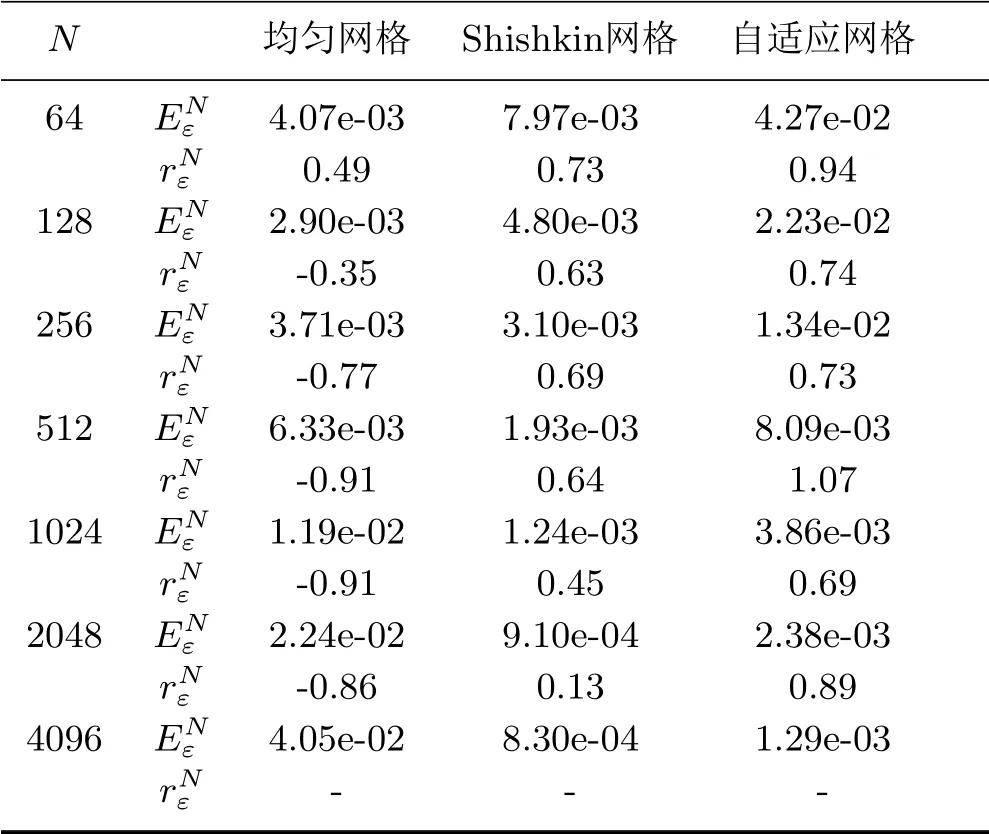
表2 不同網(wǎng)格下的數(shù)值結(jié)果比較(ε=10－5)

圖1 網(wǎng)格迭代過程(ε=10－7，N =64)

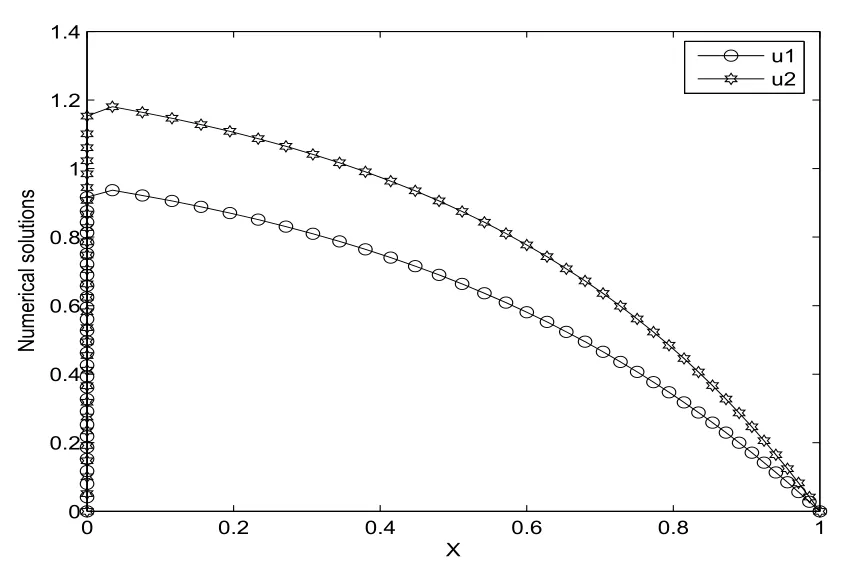
圖2 數(shù)值解的曲線圖(ε=10－7，N =64)

6.結(jié)論

本文主要從先驗誤差估計的角度，分析了一類奇異攝動對流擴散方程組的自適應(yīng)網(wǎng)格算法的收斂性.首先，利用迎風有限差分格式，在任意的非均勻網(wǎng)格上對方程組進行了離散，并給出了相應(yīng)的局部截斷誤差.然后，使用精確解的穩(wěn)定性估計、網(wǎng)格等分布原理和極大值原理等技術(shù)，證明了本文提出的自適應(yīng)網(wǎng)格算法是一階一致收斂的.值得一提的是本文的分析方法可以進一步推廣到其他奇異攝動微分方程組的自適應(yīng)網(wǎng)格算法的收斂性分析.