Existence and Stability of Positive Solutions to Nonlinear Delay Integro-Differential Equation on Time Scales

HU Meng (胡猛)，LV Haiyan (呂海燕)

(School of Mathematics and Statistics，Anyang Normal University，Anyang 455000，China)

Abstract: This paper studies the existence and stability of positive solutions for a class of nonlinear delay integro-differential equation on time scales.By using Schauder’s fixed point theorem and the theory of dynamic equations on time scales，sufficient conditions for the existence of positive periodic solutions in shifts δ± and positive solutions，and sufficient conditions for the exponential stability of positive solution of the equation are obtained，respectively.Finally，two examples are given to illustrate the usefulness of the main results.

Key words: Time scale; Integro-differential equation; Schauder’s fixed point theorem;Periodic solution in shifts δ±; Positive solution; Exponential stability

1.Introduction

In this paper，we are concerned with the investigation of a nonlinear integro-differential equation on time scales of the form

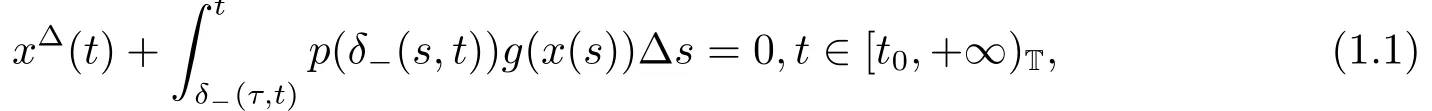
where T ?R is a time scale; p ∈Crd([t0，τ)T，R)，g ∈C((0，+∞)，(0，+∞))，and t0，τ ∈T are positive constants with τ ＞t0; the function δ-(·，t) is a delay function generated by the backward shift operator δ-on time scale T，the definitions and properties of shift operators δ±can be found in [1-3].

For T=R with δ-(s，t)=t-s and t0=0，then (1.1) reduces to the integro-differential equation of convolution type

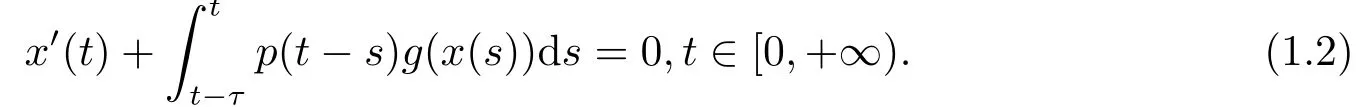
For T = Z with δ-(s，t) = t-s and t0= 0，then (1.1) reduces to the integro-difference equation of convolution type

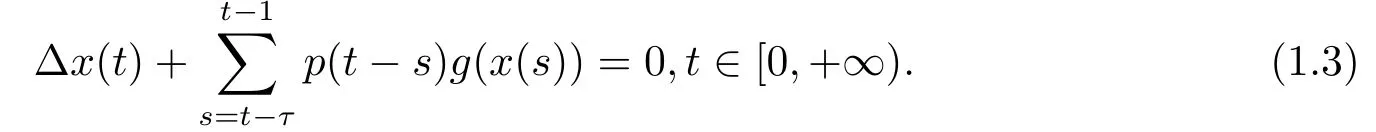
The equation (1.2) was encountered by [4] in the theory of a circulating fuel nuclear reactor.In this model，x is the neutron density.It is also a good model in one dimensional viscoelasticity in which x is the strain and p is the relaxation function.The equation (1.3)has been proposed to model some biological problems.One may see [5-7] for the researches on the equations (1.2) and (1.3).Besides (1.2) and (1.3)，equation (1.1) includes many other types equations in particular cases.

The theory of time scales was introduced in [8].The time scale theory provides a wide perspective for the unification of discrete and continuous analyses.In recent years，the existence problem of positive solution is an important topic in qualitative analysis of functional dynamic equations on time scales.[9-10]Up to now，the existence and boundedness of the solutions of nonlinear system of Volterra type integro-differential equations on time scales has been investigated in [1-2，11].However，the existence positive solutions of integro-differential equations of the form (1.1) has not been treated elsewhere before，even for the equation (1.1)on some particular time scales.

Motivated by the above statements，we bring the integro-differential equation(1.1)under investigation to obtain more general results.The main purpose of this paper is to establish sufficient conditions for the existence of positive periodic solutions in shifts δ±and positive solutions of the equation(1.1)via Schauder’s fixed point theorem.Moreover，sufficient conditions for the exponential stability of positive solution of the equation (1.1) are also explored.

2.Preliminaries

Let T be a nonempty closed subset (time scale) of R.The forward and backward jump operators σ，ρ:T →T and the graininess μ : T →R+are defined，respectively，by

σ(t)=inf{s ∈T:s ＞t}，ρ(t)=sup{s ∈T:s ＜t} and μ(t)=σ(t)-t.

A point t ∈T is called left-dense if t ＞inf T and ρ(t) = t，left-scattered if ρ(t) ＜t，right-dense if t ＜sup T and σ(t)=t，and right-scattered if σ(t)＞t.If T has a left-scattered maximum m，then Tk= T{m}; otherwise Tk= T.If T has a right-scattered minimum m，then Tk=T{m}; otherwise Tk=T.

A function f : T →R is right-dense continuous provided it is continuous at right-dense point in T and its left-side limits exist at left-dense points in T.If f is continuous at each right-dense point and each left-dense point，then f is said to be a continuous function on T.The set of continuous functions f :T →R will be denoted by C(T)=C(T，R).

A function p : T →R is called regressive provided 1+μ(t)p(t)0 for all t ∈Tk.The set of all regressive and rd-continuous functions p : T →R will be denoted by R = R(T，R).Define the set R+=R+(T，R)={p ∈R:1+μ(t)p(t)＞0，?t ∈T}.

If r is a regressive function，then the generalized exponential function eris defined by

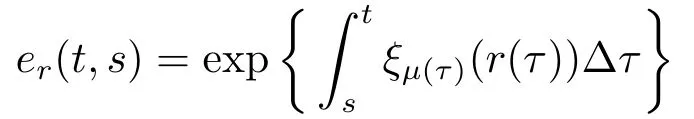
for all s，t ∈T，with the cylinder transformation

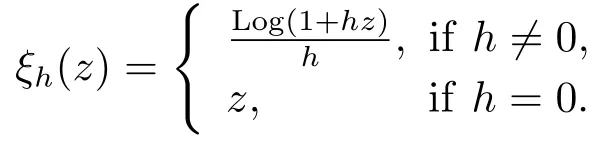
Let p，q :T →R be two regressive functions，define

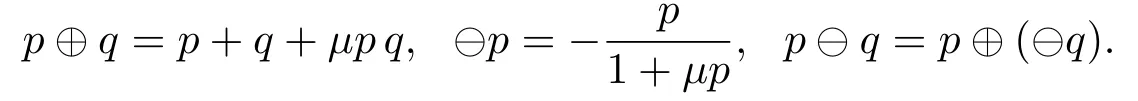
Lemma 2.1[12]Assume that p，q :T →R be two regressive functions，then

(i) e0(t，s)≡1 and ep(t，t)≡1;

(ii) ep(σ(t)，s)=(1+μ(t)p(t))ep(t，s);

(iii) ep(t，s)==e?p(s，t);

(iv) ep(t，s)ep(s，r)=ep(t，r);

(v) (e?p(t，s))Δ=(?p)(t)e?p(t，s);

A comprehensive review on the shift operators δ±and the new periodicity concepts on time scales can be found in [13-14].

Let T*be a non-empty subset of the time scale T and t0∈T*be a fixed number.Define operators δ±:[t0，+∞)×T*→T*.The operators δ+and δ-associated with t0∈T*(called the initial point) are said to be forward and backward shift operators on the set T*，respectively.The variable s ∈[t0，+∞)Tin δ±(s，t)is called the shift size.The value δ+(s，t)and δ-(s，t)in T*indicate s units translation of the term t ∈T*to the right and left，respectively.The sets

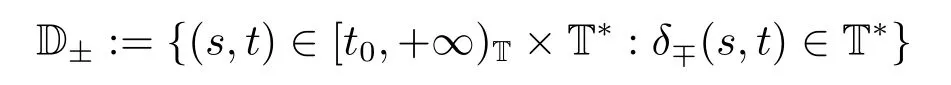
are the domains of the shift operator δ±，respectively.Hereafter，T*is the largest subset of the time scale T such that the shift operators δ±:[t0，+∞)×T*→T*exist.

Definition 2.1[14](Periodicity in shifts δ±) Let T be a time scale with the shift operators δ±associated with the initial point t0∈T*.The time scale T is said to be periodic in shifts δ±if there exists p ∈(t0，+∞)T*such that (p，t)∈D±for all t ∈T*.Furthermore，if

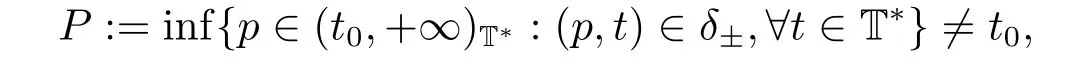
then P is called the period of the time scale T.

Definition 2.2[14](Periodic function in shifts δ±) Let T be a time scale that is periodic in shifts δ±with the period P.We say that a real-valued function f defined on T*is periodic in shifts δ±if there exists ω ∈[P，+∞)T*such that (ω，t) ∈D±and f((t)) = f(t) for all t ∈T*，where=δ±(ω，t).The smallest number ω ∈[P，+∞)T*is called the period of f.

The following fixed point theorem will be used to prove the main results in the next two sections.

Theorem 2.1[15-16](Schauder’s fixed point theorem) Let Ω be a closed，convex and nonempty subset of a Banach space X.Let S : Ω →Ω be a continuous mapping such that SΩ is a relatively compact subset of X.Then S has at least one fixed point in Ω.That is there exists an x ∈Ω such that Sx=x.

3.Positive Periodic Solutions in Shifts δ±

In this section we shall study the existence of positive ω-periodic solutions in shifts δ±of the equation (1.1).

Lemma 3.1Suppose that there exists a positive continuous function k(t，s)，s ∈[δ-(τ，t)，t]T，such that

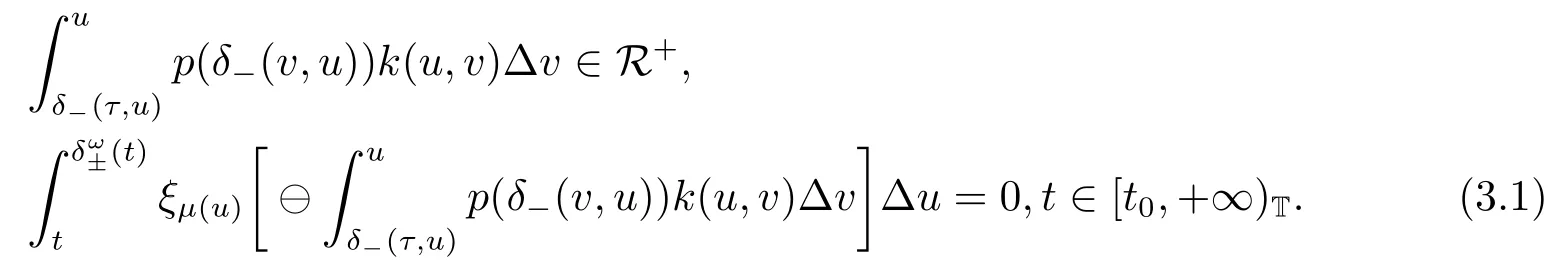
Then the function

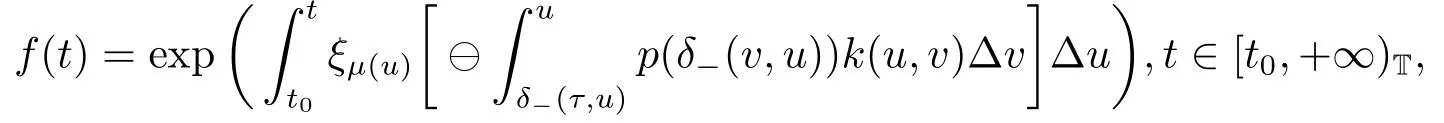
is ω-periodic in shifts δ±.

ProofFor t ∈[t0，+∞)T，we obtain

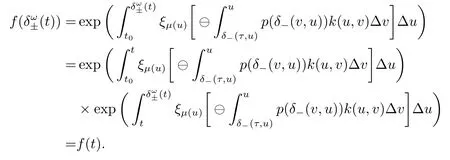
Thus the function f is ω-periodic in shifts δ±.The proof is complete.

Theorem 3.1Suppose that there exists a positive continuous function k(t，s)，s ∈[δ-(τ，t)，t]T，such that (3.1) holds and

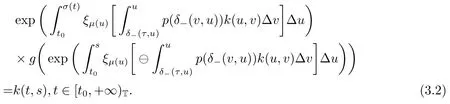
Then (1.1) has a positive ω-periodic solution in shifts δ±.

ProofLet X =Crd([δ-(τ，t0)，+∞)T，R) be a Banach space with the norm

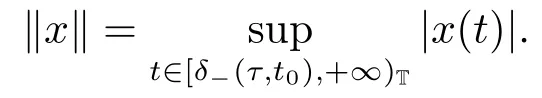
We set

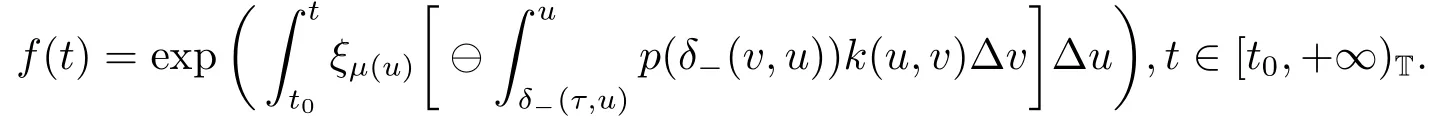
With regard to Lemma 3.1 we have m ≤f(t)≤M，where

We now define a closed，bounded and convex subset Ω of X as follows

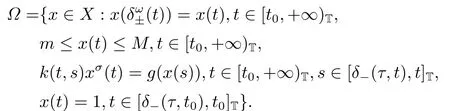
Define the operator S :Ω →X as follows

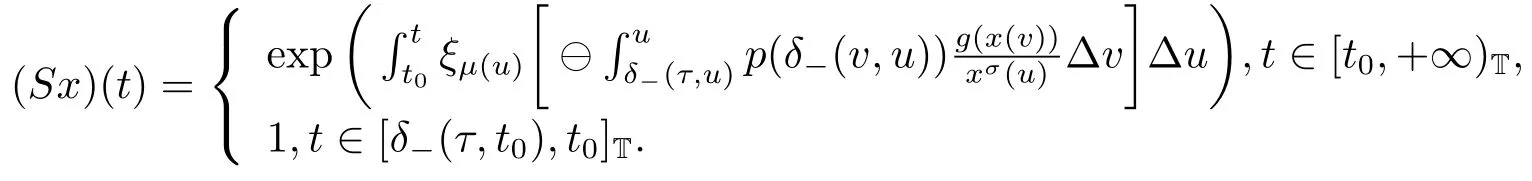
We shall show that for any x ∈Ω we have Sx ∈Ω.

For every x ∈Ω and t ∈[t0，+∞)Twe get

and (Sx)(t)≥m.

For t ∈[δ-(τ，t0)，t0]Twe have (Sx)(t)=1，that is (Sx)(t)∈Ω.

Further for every x ∈Ω and t ∈[t0，+∞)T，s ∈[δ-(τ，t0)，t]T，according to(3.2)it follows

Finally we shall show that for x ∈Ω，t ∈[t0，+∞)T，the function Sx is ω-periodic in shifts δ±.For x ∈Ω，t ∈[t0，+∞)Tand with regard to (3.1) we get

that is，Sx is ω-periodic in shifts δ±on [t0，+∞)T.Thus we have proved that Sx ∈Ω for any x ∈Ω.

We now show that S is completely continuous.First we shall show that S is continuous.Let xi∈Ω be such that xi→x ∈Ω as i →∞.For t ∈[t0，+∞)Twe have

then we obtain that

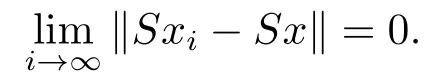
For t ∈[δ-(τ，t0)，t0]T，the relation above is also valid.This means that S is continuous.

We now show that SΩ is relatively compact.It is sufficient to show by the Arzela-Ascoli theorem that the family of functions {Sx:x ∈Ω} is uniformly bounded and equicontinuous on [δ-(τ，t0)，+∞)T.The uniform boundedness follows from the definition of Ω.According to (3.3) for t ∈[t0，+∞)Tand x ∈Ω，we get

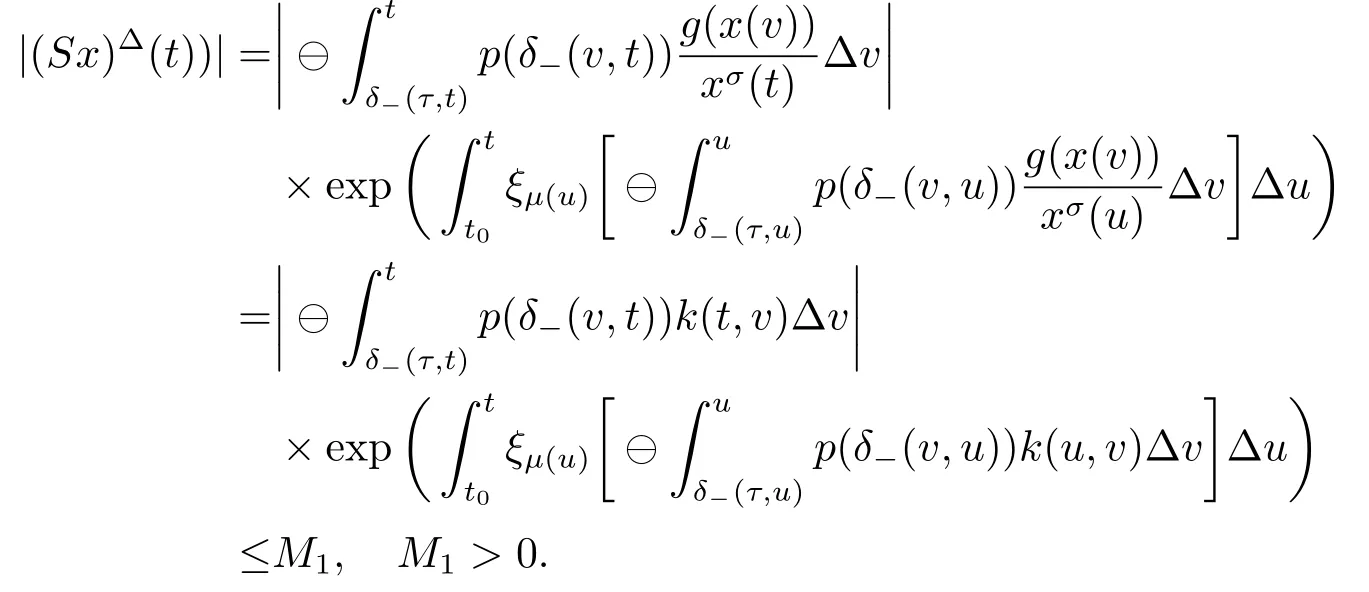
For t ∈[δ-(τ，t0)，t0]Tand x ∈Ω，we have

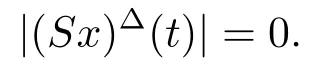
This shows the equicontinuity of the family SΩ.Hence SΩ is relatively compact and therefore S is completely continuous.By Theorem 2.1 there is an∈Ω such that S=We see thatis a positive ω-periodic solution in shifts δ±of (1.1).The proof is complete.

Corollary 3.1Suppose that there exists a positive continuous function k(t，s)，s ∈[δ-(τ，t)，t]T，such that (3.1) holds and

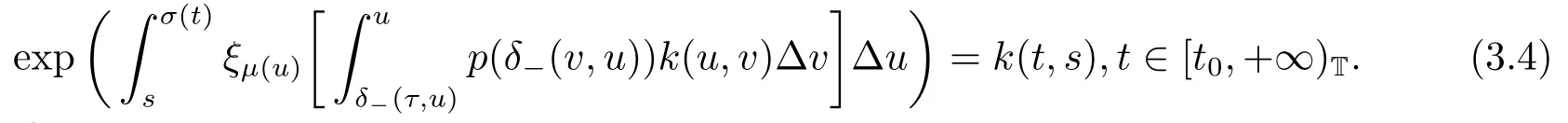
Then the equation

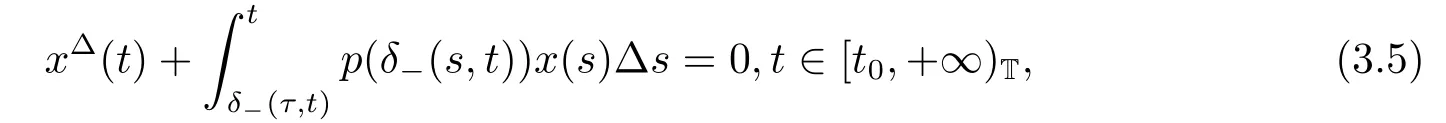
has a positive ω-periodic solution in shifts δ±

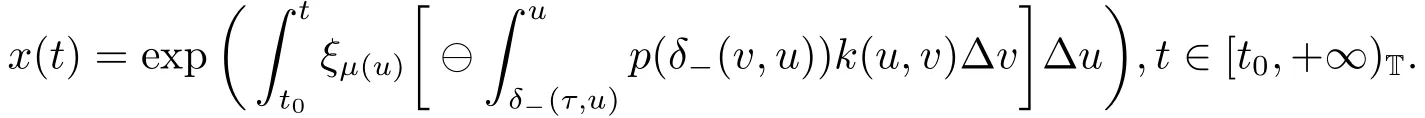
4.Positive Solutions

In this section we shall study the existence of positive solutions of the equation (1.1).

Theorem 4.1Suppose that there exists a positive continuous function k(t，s)，s ∈[δ-(τ，t)，t]T，such that (3.2) holds and

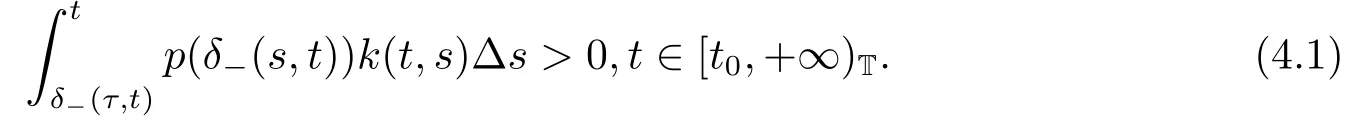
Then (1.1) has a positive solution

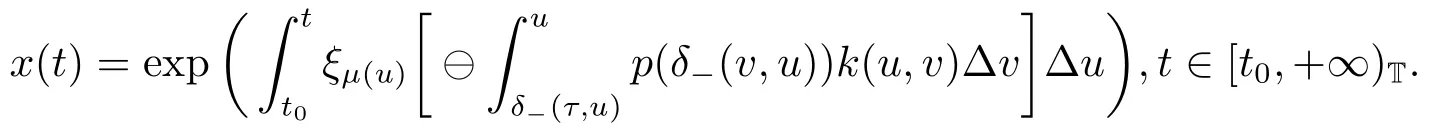
ProofLet X1= x ∈Crd([δ-(τ，t0)，+∞)T，R) be the set of all rd-continuous bounded functions.Then X1is a Banach space with the norm ‖x‖=supt∈[δ-(τ，t0)，+∞)T|x(t)|.We set

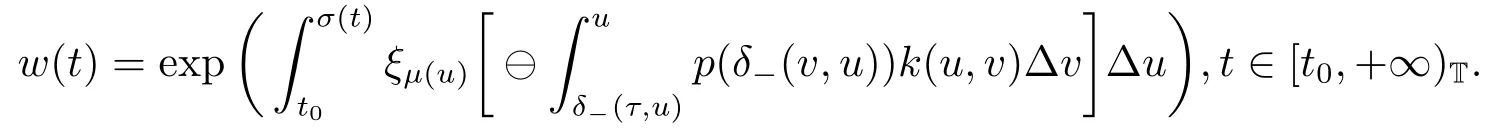
We define a closed，bounded and convex subset Ω1of X1as follows

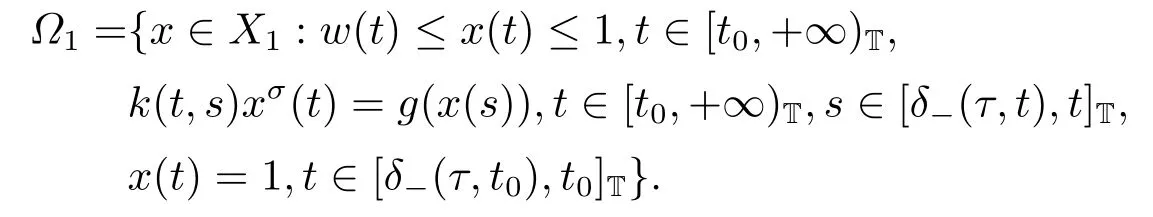
Define the operator S1:Ω1→X1as follows

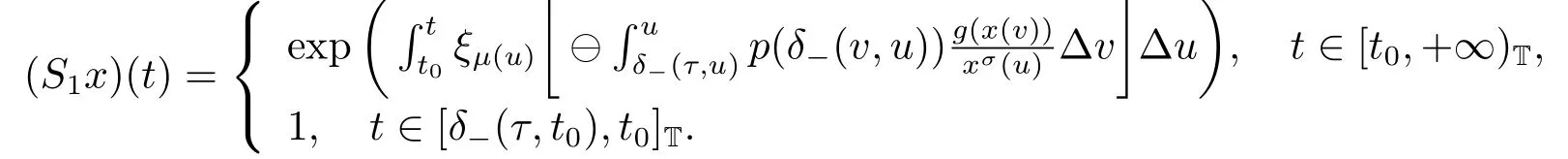
For every x ∈Ω1and t ∈[t0，+∞)T，we obtain

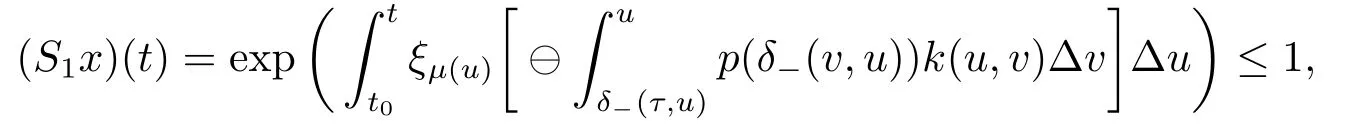
and (S1x)(t) ≥w(t).For t ∈[δ-(τ，t0)，t0]Twe get (S1x)(t) = 1，that is (S1x)(t) ∈Ω.Now we can proceed by the similar way as in the proof of Theorem 3.1.We omit the rest of the proof.

Corollary 4.1Assume that there exists a positive and continuous function k(t，s)，s ∈[δ-(τ，t)，t]T，such that (3.4) and (4.1) hold.Then (3.5) has a positive solution

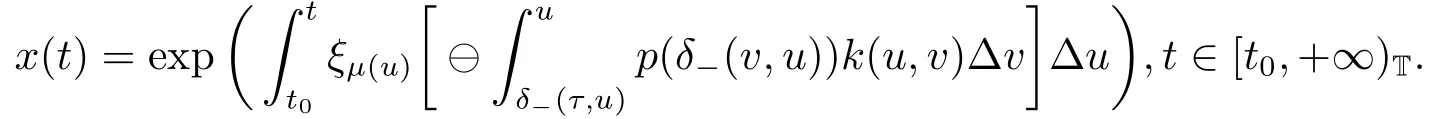
Corollary 4.2Assume that there exists a positive and continuous function k(t，s)，s ∈[δ-(τ，t)，t]T，such that (3.2) and (4.1) hold and

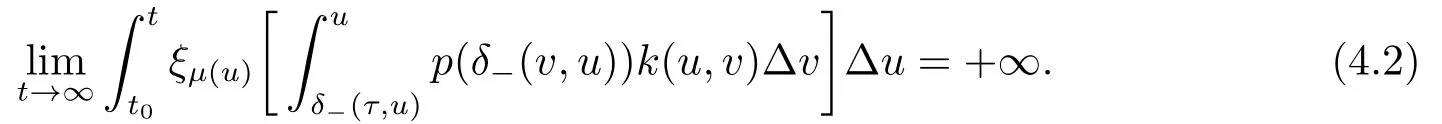
Then (1.1) has a positive solution which tends to zero.

Corollary 4.3Assume that there exists a positive and continuous function k(t，s)，s ∈[δ-(τ，t)，t]T，such that (3.2) and (4.1) hold and

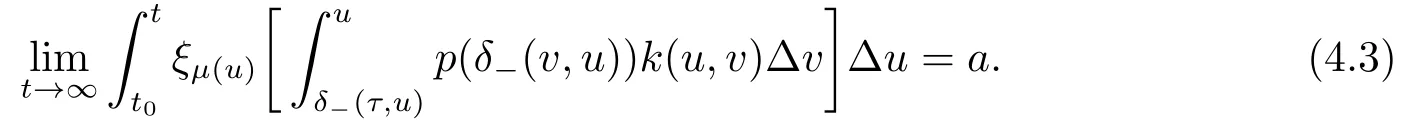
Then (1.1) has a positive solution which tends to constant e?a.

5.Exponential Stability

In this section，we shall study the exponential stability of positive solution of (1.1).We denote x(t;t0，φ)，t ∈[δ-(τ，t0)，+∞)T，for a solution of (1.1) satisfying the initial condition x(s;t0，φ) = φ(s) ＞0 for s ∈[δ-(τ，t0)，t0]T.Let x(t) = x(t;t0，φ)，x1(t) = x(t;t0，φ1) and y(t)=x(t)-x1(t)，t ∈[δ-(τ，t0)，+∞)T.Then we get

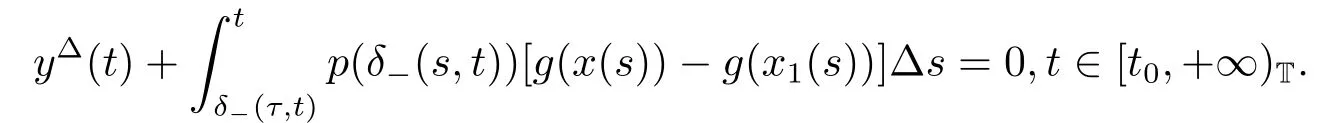
By the mean value theorem we obtain

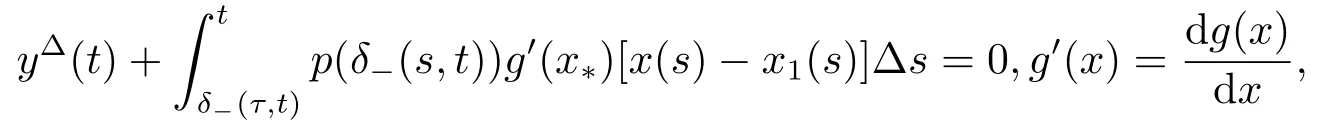
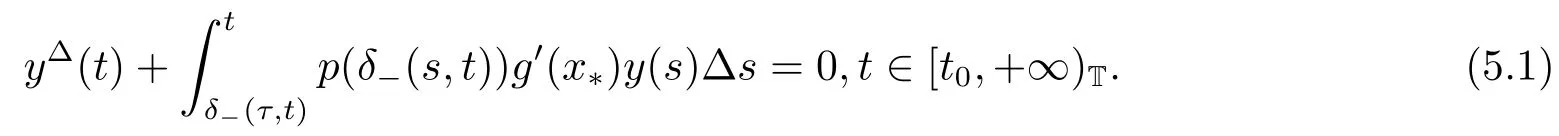
Definition 5.1Let x1be a positive solution of(1.1)and there exist constants Tφ，x1，Kφ，x1and λ ＞0 such that for every solution x(t;t0，φ) of (1.1)

|x(t;t0，φ)-x1(t)|≤Kφ，x1e?λ(t，0)，t ≥Tφ，x1.

Then x1is said to be exponentially stable.

Theorem 5.1Suppose that (3.2) and (4.1) hold and

p ∈Crd([0，τ]T，(0，+∞])，g ∈C1((0，+∞)，(0，+∞))，g′(x)≥c ＞0.

Then (1.1) has a positive solution which is exponentially stable.

ProofWe shall show that there exists a positive λ such that

|x(t;t0，φ)-x1(t)|≤Kφ，x1e?λ(t，0)，t ∈[T1，+∞)T，T1≥δ+(τ，t0)，

where Kφ，x1=maxt∈[δ-(τ，t0)，T1]T|y(t)|eλ(T1，0)+1.

Consider the following Lyapunov function

V(t)=|y(t)|eλ(t，0)，t ∈[T1，+∞)T.

We claim that V(t) ≤Kφ，x1for t ∈[T1，+∞)T.On the other hand，there exists t*∈[T1，+∞)T，and t*is the first constant such that V(t*)=Kφ，x1or V(t*)＞Kφ，x1.Calculating the upper left derivative of V(t) along the solution y of (5.1)，we obtain

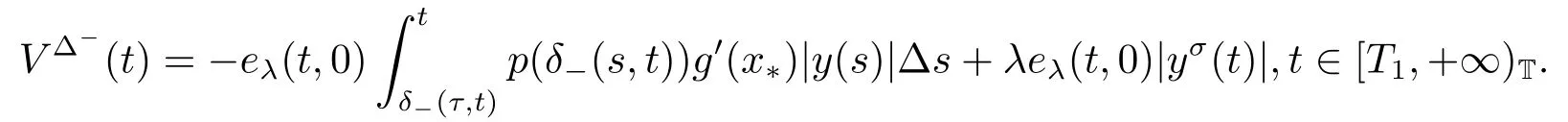
For t=t*，we get

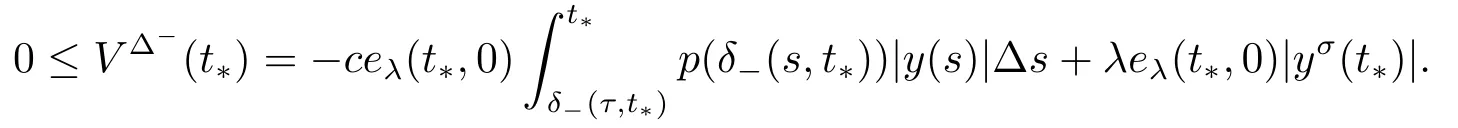
If y(t) ＞0，t ∈[t0，+∞)T，then from (5.1) it follows that for t ∈[T1，+∞)Tthe function y is decreasing and if y(t)＜0，t ∈[t0，+∞)T，then y is increasing for t ∈[T1，+∞)T.We conclude that |y(t)|，t ∈[T1，+∞)Thas decreasing character.Then we obtain

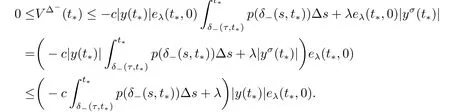
6.Examples

In this section，we give two examples to illustrate our main results.Consider the nonlinear integro-differential equation

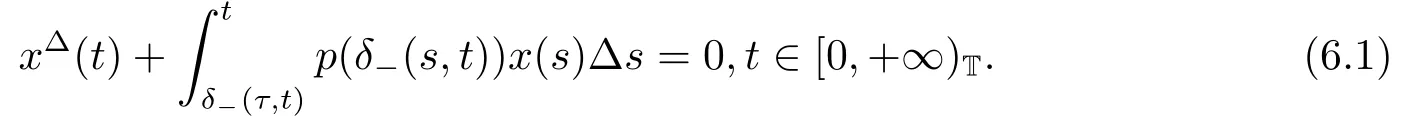
Example 1If T=R.Let p(t)=π sin(πt)，then ω =2，we choose

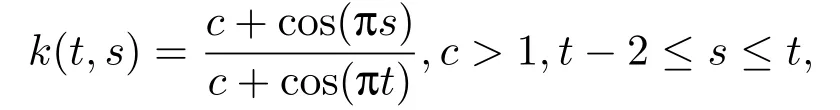
and τ =2.

Then for the condition (3.1)，we have

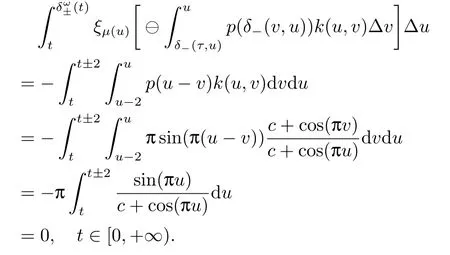
For the condition (3.4)，we have

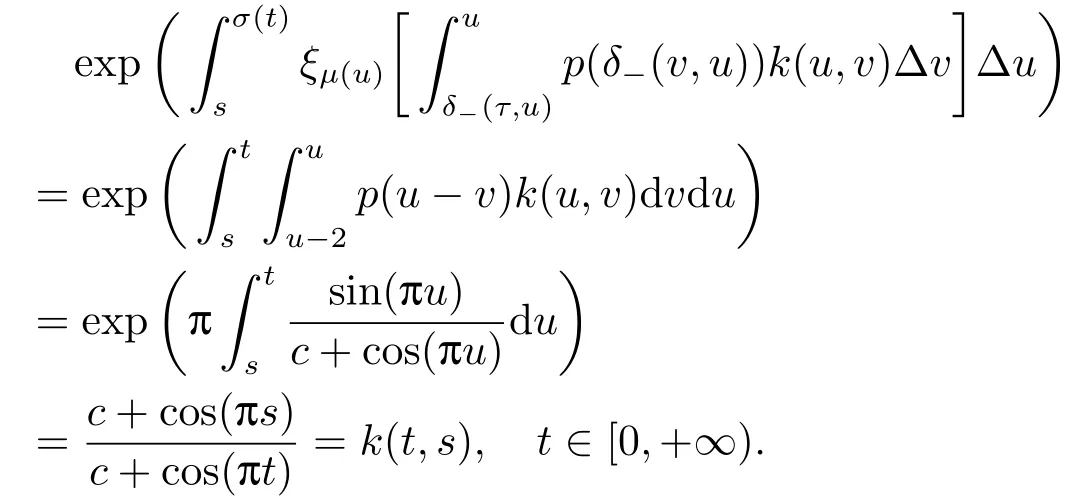
All conditions of Corollary 3.1 are satisfied and the equation(6.1)has a positive 2-periodic solution in shifts δ±

Example 2If T=Z.Letwe choose

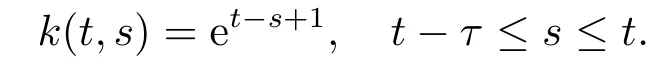
Then for the condition (3.2)，we have

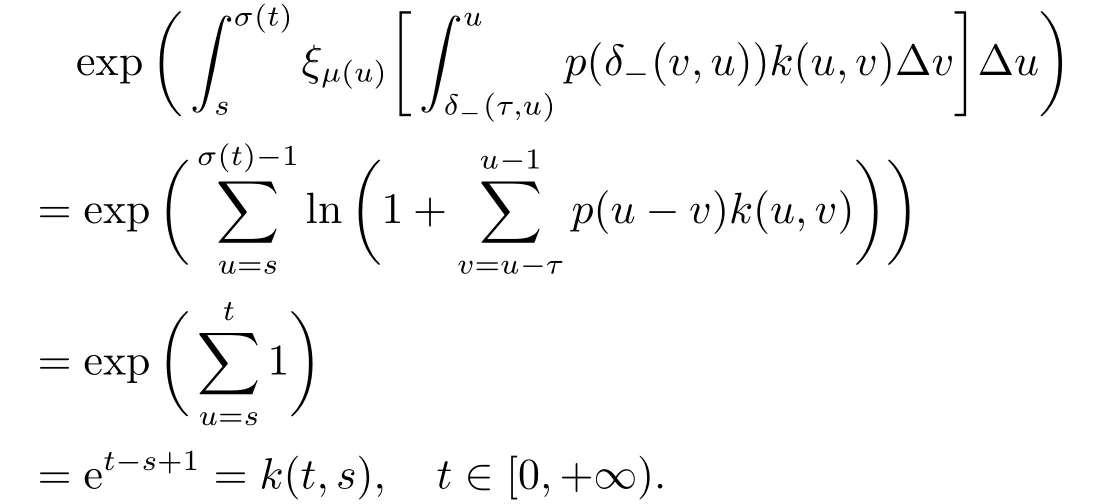
For the condition (4.2)，we have

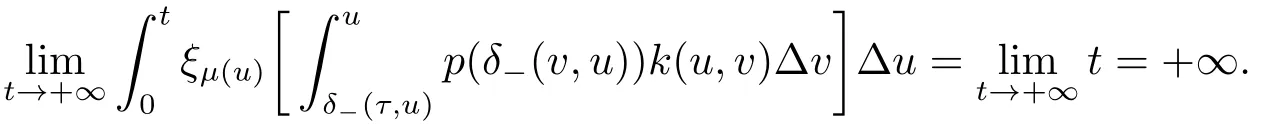
All conditions of Corollary 4.2 are satisfied and the equation(6.1)has a positive solution

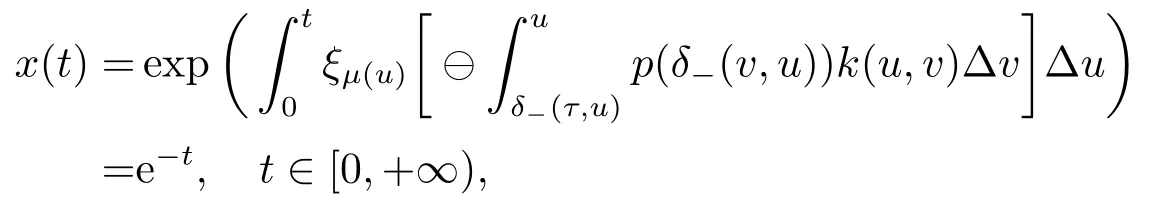
that is，(6.1) has a positive solution which tends to zero.