Impulsive Control for One Class of the Incommensurate Conformable Fractional Order System with Discontinuous Right Side
GAO Yang(高揚)
(Department of Teaching Education,Daqing Normal University,Daqing 163712,China)
Abstract: In this paper,one class of the incommensurate conformable fractional order system with discontinuous right side (DICFS) is studied.Firstly,the existence of the Filippov solution for the incommensurate conformable fractional order discontinuous system is obtained.Secondly,the comparison theorem is constructed for the incommensurate fractional discontinuous system.Moreover,by using the method of the eigenvalue and Lyapunov theory,two theorems that the incommensurate conformable fractional order discontinuous system is fractionally exponentially stable by impulsive control are derived.Finally,one example is given to illustrate applications of main results.
Key words: Fractionally exponentially stable; Filippov solution; Impulsive control;Conformable fractional-order derivative
1.Introduction
In recent years,the fractional order system has attracted many researches.Due to it can be applied in the fields of physics and engineering extensively,see the literatures [1-16].
Both Riemann-Liouville (RL) and Caputo fractional order derivative are used generally .While,two kinds of fractional order definitions share some weaknesses.For example,the monotonicity of a function f cannot be determined from the RL or Caputo fractional derivative of f.Recently,Khalil[6]gave a new fractional derivative definition named as conformable fractional derivative.Abdeljawad[7]developed the conformable fractional derivative.The stability and asymptotic stability of conformable fractional-order nonlinear systems by using Lyapunov function were obtained in [9].In comparison with the RL and Caputo fractional derivative,the conformable fractional derivative maybe suitable choice,because the conformable fractional derivative can be seen as a natural extension of the usual derivative.
The study about stability and stabilization for the incommensurate fractional-order system is an interesting topic.[10-15]Stability results about the commensurate fractional-order system maybe not valid for the incommensurate fractional-order system.Therefore,it is important to study the incommensurate fractional-order system.
In [12],an impulsive incommensurate fractional order system was considered as follows:
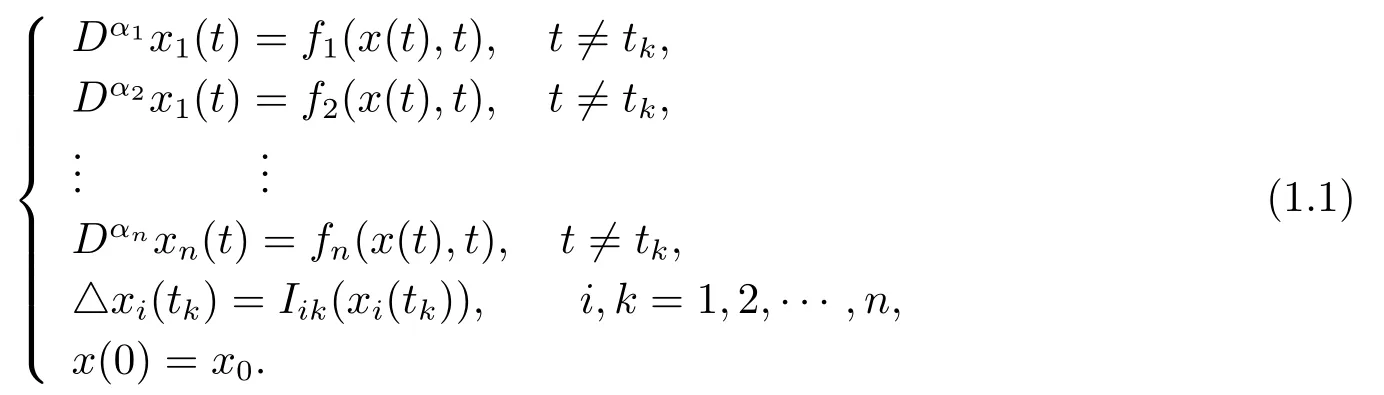
where x=(x1,·,xn)Twas the state variable,0 <α1≤α2≤···≤αn≤1 were the orders of Caputo fractianal derivatives.fi(x(t),t)(i=1,2,··· ,n)were λ-Lipschtiz nonlinear functions.Δxi(tk)=xi()-xi(tk).The stability of impulsive incommensurate fractional order chaotic systems with Caputo derivative was investigated in [12].Some novel stability criteria for impulsive incommensurate fractional order systems were proposed.
As far as we know,most of researchers are interested in the commensurate fractional-order system.To the best of authors’ knowledge,there are less results about the incommensurate fractional-order discontinuous system.In this paper,the incommensurate conformable fractional order system with discontinuous right side is considered.Firstly,the existence of the Filippov solution for DICFS is obtained.Secondly,the comparison theorem is constructed for DICFS.Moreover,by using the method of the eigenvalue and Lyapunov theory,two theorems that the incommensurate conformable fractional order discontinuous system is fractionally exponentially stable by impulsive control are derived.Finally,one example is given to illustrate applications of main results.Main results can be regarded as the generalization of [12].
Our innovation points are listed as follows.Firstly,the incommensurate fractional-order discontinuous system with the Filippov solution and conformable fractional derivative is modeled.Secondly,New comparison theorem for the incommensurate conformable fractional discontinuous system is showed and used to study stability for the new system.Finally,the Lyapunov theory is applied to the incommensurate conformable fractional order discontinuous system’s impulsive stabilization.
This paper is organized as follows.Preliminary results are introduced in Section 2.In Section 3,main results are obtained.In the sequel,an example is presented in Section 4.Finally,the conclusions and outlooks are drawn in Section 5.
2.Preliminaries
In this section,we will list some definitions and Lemmas which will be used in the later sections.
Definition 2.1[1]The Caputo fractional derivative of order α ∈(n-1,n) for a continuous function f :R+→R is given by

Definition 2.2[6]Given a function h defined on an [a,∞),the conformable fractional derivative starting from a of a function h of order α is defined by

for all t >a,α ∈(0,1].
Lemma 2.1[9]Let h : [a,∞) →R be a continuous function such that(t) exists on (a,∞).If(t) ≥0 (respectivelyt) ≤0),for all t ∈(a,∞) then the graph of h is increasing (respectively decreasing).
Definition 2.3[9]The fractional conformable exponential function is defined for every s ≥0 by
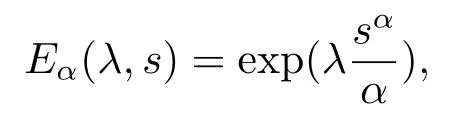
where α ∈(0,1) and λ ∈R.
Lemma 2.2[9]The origin of system

is said to be fractionally exponentially stable if

where λ,K >0.
Lemma 2.3If α ∈(0,1],x >0,b >0,then (x+b)α≤xα+bαholds.
ProofLet

Therefore,we obtain

In the sequel,f(x) is decreasing in the interval (0,+∞).Note f(x) is continuous about 0,we have f(x)≤f(0).Hence f(x)≤0 holds.
Then the inequality’s proof is completed.
Lemma 2.4If α ∈(0,1],λ >0,a >0,b >0,then
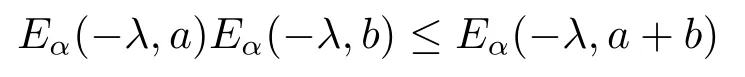
holds.
ProofBy Lemma 2.3,we have

Furthermore,

Therefore,the proof is completed.
Lemma 2.5If α,β ∈(0,1],α ≤β,λ >0,a ∈(0,1],b >0,then

holds.
ProofLet

Thus,we obtain

In the sequel,f(x) is decreasing in the interval (0,1].Noting α ≤β,we have

So

holds.
Then we get

By Lemma 2.4,we have

Furthermore,we obtain

So the inequality’s proof is completed.
Lemma 2.6If α,β ∈(0,1],α ≤β,λ >0,a ∈(0,1],then

and Eβ(λ,a)≤Eα(λ,a) hold.
ProofBy Lemma 2.5,we obtain

holds.
Therefore,the inequalities hold.The proof is completed.
Lemma 2.7Suppose x(t)is absolutely continuous on any compact interval of[0,+∞),then for any i=1,2,··· ,n,
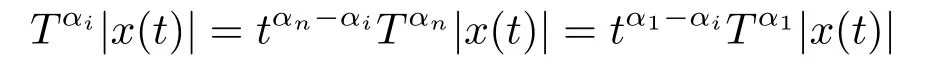
holds for almost every t ∈[0,+∞) with 0 <α1≤α2≤···≤αn≤1.
ProofBecause x(t) is absolutely continuous on any compact interval of [0,+∞),we obtain that |x(t)| is absolutely continuous on any compact interval of [0,+∞).Furthermore,|x(t)| is differentiable almost everywhere with respect to t ∈[0,+∞).Assume that |x(t)|′exists at time t.In the sequel,we have

Then we obtain

holds for almost every t ∈[0,+∞) .Similarly,
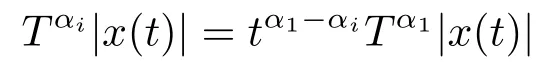
holds for almost every t ∈[0,+∞).
The proof is completed.
3.Main Results
An incommensurate conformable fractional order system with discontinuous right side is constructed as follows:

where x = (x1,·,xn)Tis the state variable,0 <α1≤α2≤··· ≤αn≤1 are orders of Conformable fractianal derivatives.fi(x(t),t)(i=1,2,··· ,n)are λ-Lipschtiz nonlinear functions.

Remark 3.1Ii(xi)(i = 1,2,··· ,n) can be seen as the threshold policy in the ecology system.Because it is natural and reasonable to adopt the threshold policy in order to control the population density of species.Moreover,Ii(xi)(i=1,2,··· ,n) can be seen as the discontinuous activation function of the ith neuron in Hopfield neural networks,such as hard comparator.Therefore,the new discontinuous system is reasonable.
Let

The incommensurate conformable fractional order discontinuous system (3.1) is equivalent to the system as follows:

Based on the Filippov solution of integer order system,the concept of Filippov solution for the incommensurate conformable fractional order discontinuous system is given as follow.
The set-valued maps can be denoted as

Definition 3.1A function x(t) is called as a Filippov solution of system (3.1) on interval [0,T) with the initial condition x(0) = x0,if x(t) is absolutely continuous on any compact interval of [0,T) and

for almost every t ∈[0,T).Or there exists a measurable function(measurable selection of the function I ) γ =(γ1,γ2,··· ,γn),such that γ(t)∈I(x(t)) and
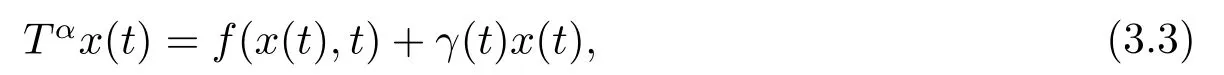
for almost every t ∈[0,T).
Now we will discuss the existence of the solution for incommensurate conformable fractional order discontinuous system (3.1) by the fractional-order differential inclusion.
Theorem 3.1In the sense of (3.3) ,there exists at least one solution of system (3.1)in the interval [0,+∞) for any initial value x(0).
ProofBecause the set-valued map Tαx(t)F(x(t),t) is upper-semi-continuous with nonempty compact convex values,the local existence of a solution x(t) of (3.1) can be guaranteed.
Indeed,we obtain |Fi(xi)|=supξ∈Fi(xi)|ξ|≤(λ+1)|xi|.
Firstly,?t ∈[0,1],the integral equation is obtained as follows:

Furthermore,we obtain

According to the Gronwall inequality,we obtain

So x(t) remains bounded for t ∈[0,1],which ensures that the solution of system (3.1) exists in the interval [0,1].
Secondly,?t ∈[1,+∞),we have

According to the Gronwall inequality,we obtain

So x(t) remains bounded for t ∈[1,+∞),which ensures that the solution of system (3.1)exists in the interval [1,+∞).
Finally,x(t) remains bounded for t ∈[0,+∞),which ensures that the solution of system(3.1) exists in the interval [0,+∞).
In order to research impulsive control for the incommensurate conformable fractional order discontinuous system (3.1),new comparison theorems are constructed as follows.We introduce another system which is defined as:

New comparison theorems are constructed as follows.
Theorem 3.2For the systems (3.2) and (3.4),if fi(x(t),t)+γi(t)xi(t)≤gi(y(t)) hold almost everywhere and xi0≤yi0,then xi(t)≤yi(t)(i=1,2,··· ,n).
ProofAccording to the definition of the Filippov solution,we obtain that x(t),y(t)are absolutely continuous on any compact interval of [0,T).In the sequel,x(t),y(t) are locally absolutely continuous.Furthermore,x(t),y(t) are differentiable almost everywhere with respect to t.
By the condition of this theorem,we obtain that

hold for almost every t ≥0.
Choose the time t such that both x(t) and y(t) exist.Therefore,

The proof is completed.
Based on Theorem 3.2,the following corollary is obtained naturally.
Corollary 3.1For the systems (3.2) and (3.4),if |fi(x(t),t)+γi(t)xi(t)| ≤gi(y(t))and |xi0|≤yi0,then |xi(t)|≤yi(t)(i=1,2,··· ,n).
Consider the impulsive discontinuous system as follows:

Therefore,the following corollary is obtained naturally.
Corollary 3.2For the systems (3.5) and (3.6),if |fi(x(t),t)+γi(t)xi(t)| ≤gi(y(t))(a.e.t) andthen |xi(t)|≤yi(t)(i=1,2,··· ,n).
ProofRepeating using Theorem 3.2 in the interval [tk,tk+1] and the factwe can obtain Corollary 3.2.
Note that fi(x(t),t) are λ-Lipschitz,|γ(t)|≤1 and

New comparison system for the system (3.6) is obtained as follows.

where

Let an orthogonal matrix

and y(t)=Mz(t).The equivalent system of (3.7) is obtained as follows:

where

For the system (3.8),the following theorem is given.
Theorem 3.3If τk= tk-tk-1<1 and dik= Eαi(-2(nλ+1),τk) ,then the trivial solution zi=0 of system (3.8) is fractionally exponentially stable with=dikzi(tk) .
ProofFor any t ∈[0,t1],we obtain

and

In the sequel,for any i=1,2,··· ,n ,we have

Moreover,we get

In general,for t ∈(tk-1,tk],we have

This means the trivial solution zi=0 of system(3.8)is fractionally exponentially stable.The proof is completed.
Then the impulsive control of the incommensurate conformable fractional order discontinuous system can be realized as follows:
Theorem 3.4If τk=tk-tk-1<1,dik=Eαi(-2(nλ+1),τk),then impulsive control can stabilized the system (3.1) withThis means that the trivial solution xi=0 of system (3.5) is fractionally exponentially stable.
ProofBy Theorem 3.3 and y(t)=Mz(t),we obtain

This demonstrates that the systems (3.7) and (3.8) are fractionally exponentially stable.We can choose
With the help of new comparison theorem(Theorem 3.2),we obtain the trivial solution xi=0 of system(3.5)is fractionally exponentially stable.Then impulsive control can stabilize system (3.1).
In the next part,we will design a new comparison system for the incommensurate conformable fractional order discontinuous system (3.5) based on (3.6).Using Lemma 2.7,for any t ∈[0,1],we have tαi-α1≤1,and Tαiyi(t)=tα1-αiTα1yi(t)=gi(y(t)).
Hence,Tα1yi(t)=tαi-α1Tαiyi(t)≤gi(y(t)).
While,for any t ∈[1,+∞),tαi-αn≤1,and

Hence,

The new comparison system is constructed as follows:

Therefore,the following corollary is obtained naturally.
Corollary 3.3For the systems (3.6) and (3.9),if gi(y(t)) ≤gi(z(t)) (a.e.t) andthen yi(t)≤zi(t)(i=1,2,··· ,n).
Hence the impulsive control of the incommensurate conformable fractional order discontinuous system can be realized as follows:
Theorem 3.5If
holds for almost everywhere with respect to t and τk= tk-tk-1<1,λ >0 ,dik= dk=Eα1(-λ,τk),then the trivial solution zi=0 of system(3.9)is fractionally exponentially stable.This means that impulsive control can stabilize system (3.1) with xi(=dikxi(tk).
ProofNotice the condition (3.10),for z(t)(t ∈[0,1]),we obtain that

Therefore,for any t ∈[tk-1,tk]?[0,1] ,we get

Moreover,

and

Using Lemma 2.4,2.5,2.6,for t ∈(tk-1,tk]?[0,1],we have

and

Similarly,for t ∈(tk-1,tk]?(1,+∞),we have

Therefore,we have

This means that the trivial solution zi=0 of system(3.9)is fractionally exponentially stable.With the help of Theorem 3.2,Corollary 3.2 and Corollary 3.3,impulsive control can stabilize the system (3.1) with xi)=dikxi(tk).
4.An Example
In this section,an example is presented to illustrate Theorem 3.4 and Theorem 3.5.
Consider the following system of incommensurate conformable fractional discontinuous equation:

where α1=0.2,α2=0.5,β12=-β21=9,ε1=ε2=2 .
Model (4.1) comes from [2].In [2],LI investigated a coupled system of fractional-order differential equations on network with feedback controls.Model (4.1) can be seen as coupled system of incommensurate fractional-order differential equations on network with Threshold Policy.
A comparison system is constructed as follows.

Therefore,we have

Here,λ=22.Choose τk=tk-tk-1<1 ,dik=Eαi(-90,τk) and

Then the impulsive control can be designed to stabilize system (4.1) by Theorem 3.4 with

After calculating,we obtain

τk= tk-tk-1<1,dik= dk= Eα1(-13,τk).Then the impulsive control can be designed to stabilize the system (4.1) by Theorem 3.5 with xi=dikxi(tk).
Remark 4.1From the example,we can see that Theorem 3.5 is more convenient than Theorem 3.4 in application.While,Theorem 3.4 and Theorem 3.5 are equally effective when softwares for calculation are used by us.
5.Conclusions and Outlooks
In this paper,the incommensurate conformable fractional order system with discontinuous right side is studied.Firstly,the existence of the Filippov solution for the incommensurate conformable fractional order discontinuous system is obtained.Secondly,the comparison theorem is constructed for the new incommensurate fractional discontinuous system.Moreover,by using the method of the eigenvalue and Lyapunov theory,two theorems that the incommensurate conformable fractional order discontinuous system is fractionally exponentially stable by impulsive control are derived.Finally,an example is given to illustrate applications of main results.
Further studies on this subject are being carried out by the presenting authors in the two aspects: one is to study the model with time delay; the other is to apply the method to suitable discontinuous system.
- 應用數學的其它文章
- 一種新的二次約束二次規劃問題的分支定界算法
- 一類分數階Kirchhoff型方程Schwarz對稱基態解的存在性
- 矩陣偽譜的新定位集及其在土壤生態系統的應用
- The Uniform Boundedness and Convergence for the Core Inverses of Linear Operators in Banach Spaces
- Existence and Stability of Positive Solutions to Nonlinear Delay Integro-Differential Equation on Time Scales
- 一類奇異攝動對流擴散方程組的自適應網格方法的收斂性分析

