非線性橢圓障礙問題很弱解的全局可積性

佟玉霞，楊雅琦，周艷霞

(華北理工大學理學院，河北 唐山063210)

1.引言

設Ω ?Rn(n ≥2)是一個有界正則區域，1 ＜p ＜n，這里正則域指的是具有有限測度并使得下文Hodge分解(引理2.1)成立的區域.例如，Lipschitz域和A型區域是正則的.

令ψ為Ω中任意取值于R ∪{-∞，+∞}的函數，θ ∈W1，r(Ω).令

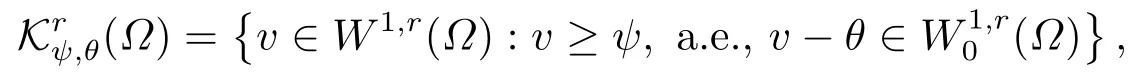
其中函數ψ為障礙函數，θ為邊值函數.

本文考慮非線性橢圓方程

并且B(x，ξ)滿足

現在介紹引理2.1中擾動向量場的Hodge分解|?(v-u)|p-2?(v-u)∈Lr/(r-p+1)(Ω):

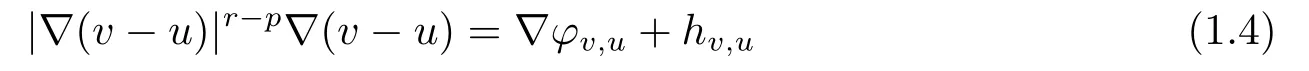
定義1.1稱為(1.1)的-障礙問題的很弱解，max{1，p-1}＜r ＜p，如果

上面定義中“很弱”的含義是指解u的可積指數r可以小于自然指數p，這不同于通常的經典弱解Ω)的假設.

首先回顧很弱解的相關進展.Iwaniec在文[1]中首次提出了很弱解的概念，對p-調和張量和弱擬正則映射，其弱導數的可積性低于自然指數.此外，Iwaniec-Sbordone[2]和Iwaniec等[3]分別考慮了變分積分的弱極小和r充分接近p時的弱p-調和型方程的正則性; 通過對擾動向量場的Hodge分解的方法，得到了變分積分的弱極小和弱p-調和方程的很弱解實際上是經典意義下的弱解.另一方面，與Iwaniec使用的方法不同的是，Lewis[4]通過調和分析技術獲得了某些橢圓型方程很弱解的高階可積性.后來，Lewis的調和分析技術又擴展到p-拉普拉斯算子[5-6]的拋物型方程組，以及各種非標準增長的橢圓和拋物型方程組[7-10].這從本質上說是使用了弱導數的逆Hlder不等式從而提高可積性來實現的[11].Greco等在文[12]中研究了非齊次p-調和方程

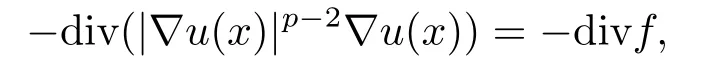
獲得了算子H的估計.鄭神州和方愛農[13]研究了非線性橢圓方程組

的很弱解，并且在擾動向量場的Hodge 分解的基礎上，得到了其很弱解的微商具有自我提高的可積性.有關很弱解的更多結果，參見[1，4，12，14].

本文研究的可積性問題在非線性橢圓偏微分方程的正則性理論和相應的障礙問題中占有重要地位.在文[15]中，GAO等研究解決在某些合適的強制性條件和控制增長條件下，一類各項異性橢圓方程

令t ＞0，Ω ?Rn，弱Lt-空間或Marcinkiewicz空間[16]指的是包含所有滿足

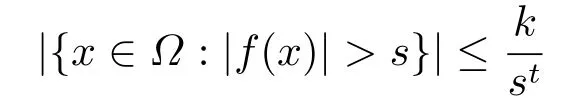
的可測函數f構成的空間，其中正常數k = k(f)，s ＞0，|E|是E的n維測度.記為弱Lt-空間或(Ω).注意到，對于某些t ＞1，|Ω| ＜∞，如果f ∈(Ω)，則對于任意的1 ≤τ ＜t，有f ∈Lτ(Ω).

本文主要結果如下.

定理1.1設θ*= max{θ，ψ}，θ*∈W1，q(Ω)，q ＞r.假設算子A(x，?u)和B(x，?u)滿足結構性條件(1.2)和(1.3).那么存在一個常數ε0= ε0(n，p，Λ1，Λ2，λ) ＞0，使得對于(1.1)的(Ω)-障礙問題的任意很弱解u ∈θ+(Ω)，max{1，p-1}＜r ＜p ＜n，有

本文證明受高紅亞和鄭神州等人的論文[13，16，19-20]的啟發，因為定義式(1.5)中很弱解不能做為容許函數，因此通過Hodge分解構造一個適當的容許函數.也就是說，本文的關鍵是通過Hodge分解選擇一個合適的容許函數[2，13]，然后根據Stampacchia引理[19]實現最終目標.需要說明的是，文[21]也考慮了一類A-調和方程的障礙問題的很弱解的全局可積性，但是其采用的方法主要是通過建立關于很弱解的梯度的弱逆Hlder不等式從而提高可積性來實現的.本文與其采用的方法是不同的.

2.預備知識

本節將介紹一些有用的引理.這些引理將在證明主要結論時起重要作用.用C(n，p，Λ1，···)表示僅依賴于規定數量的常數，各行中的常數C可能有不同.

首先，給出向量場的Hodge分解，見文[13]中的引理2.2.

引理2.1設v ∈(Ω，Rm)，max{1，p-1}＜r ＜p.則一定存在和散度自由的矩陣場h ∈(Ω，Rn×m)，使得

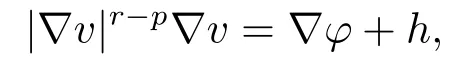
并且有估計式

其中C =C(n，p，Ω).

下面一個有效的工具就是著名的Stampacchia引理，參見文[22]中的引理4.1.

引理2.2令α，β為正常數，遞減函數φ:[s0，+∞)→[0，+∞)，滿足

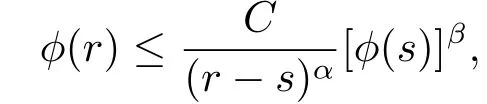
其中常數C ＞0，r ＞s ≥s0.于是

(i) 若β ＞1，則φ(s0+d)=0，這里

(ii) 若β =1，則當s ≥s0時，有

(iii) 若β ＜1，則當s ≥s0＞0時，有

3.定理1.1的證明

證令θ*=max{θ，ψ}.對于任意的L ＞0，令

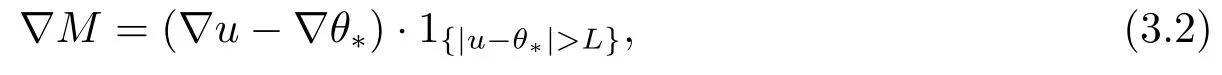
其中1{|u-θ*|＞L}是集合E的特征函數，即當x ∈E時，1E=1.否則1E=0.

令

1) 顯然v ∈W1，r(Ω);

因此(ψ-θ)+屬于因此θ*∈θ+于是在?Ω上θ*= max{θ，ψ} = θ = u，于是在?Ω上M =0，從而v ∈θ+(Ω);

3) 第一種情況，當u-θ*＜-L時，v = u-(u-θ*+L) = θ*-L ＞u ≥ψ; 第二種情況，有v =u ≥ψ; 第三種情況，v =u-(u-θ*-L)=θ*+L ≥θ*≥ψ.

因此，有

現在引入擾動向量場|?(v-u)|p-2?(v-u) ∈Lr/(r-p+1)(E)的Hodge分解，如引理2.1所示.于是，

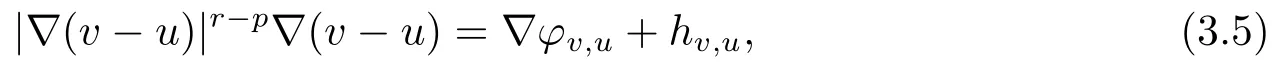
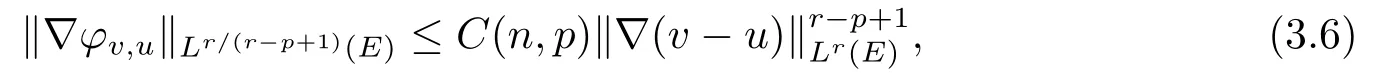
且

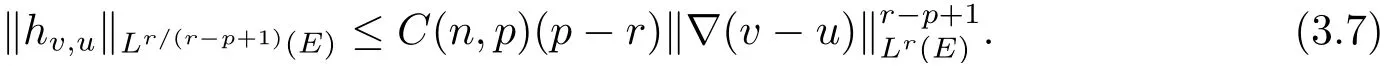
上式左側利用(1.2)，得到

這表明

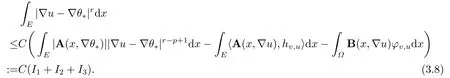
使 用(1.2)，(1.3)，(3.7)，(3.6)，Hlder不等式，Young不等式 和Sobolev-Poincar′e不等式，I1，I2，I3可估計如下:

這里ε ＞0足夠小.

這里限制0 ＜p-r ＜ε0，其中ε0為待定常數.

并且

將J1和J2的估計值放在一起，得到

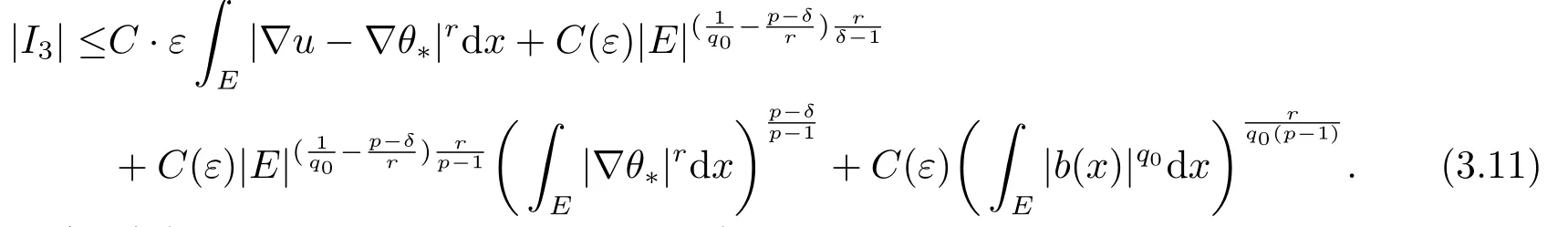
因此，結合(3.8)，(3.9)，(3.10)和(3.11)，可得

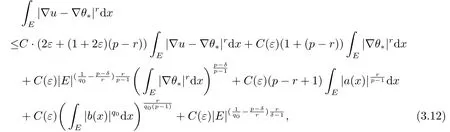
其中0 ＜p-r ＜ε0，取正常數ε，ε0足夠小，使得于是(3.12)右邊的第一項可以被左邊吸收，于是得到

由于θ*∈W1，q(Ω)，q ＞r，使用Hlder不等式可得

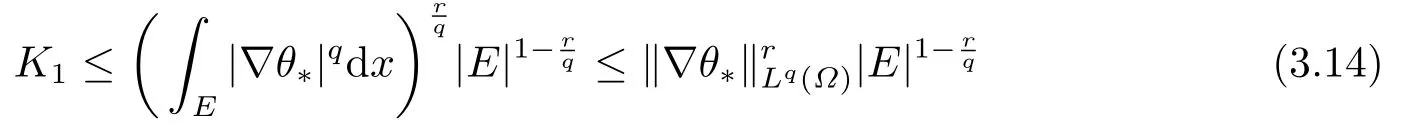
和

于是

和

于是有

將K1，K2，K3，K4和K5的估計值代入(3.13)，得到

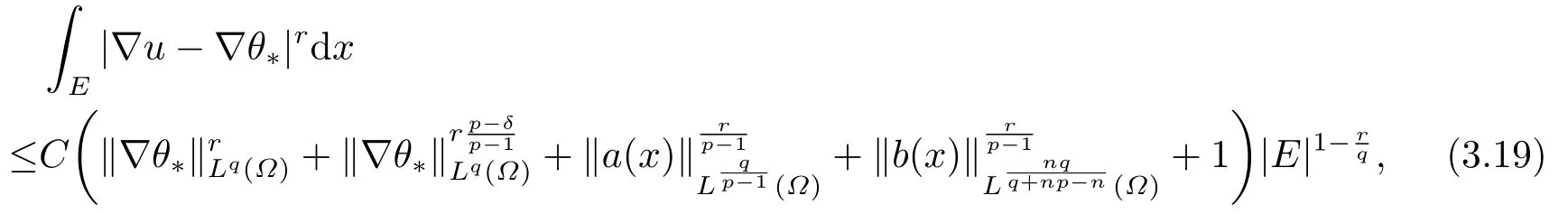
其中C =C(n，p，q，λ，Λ1，Λ2，δ，|Ω|).

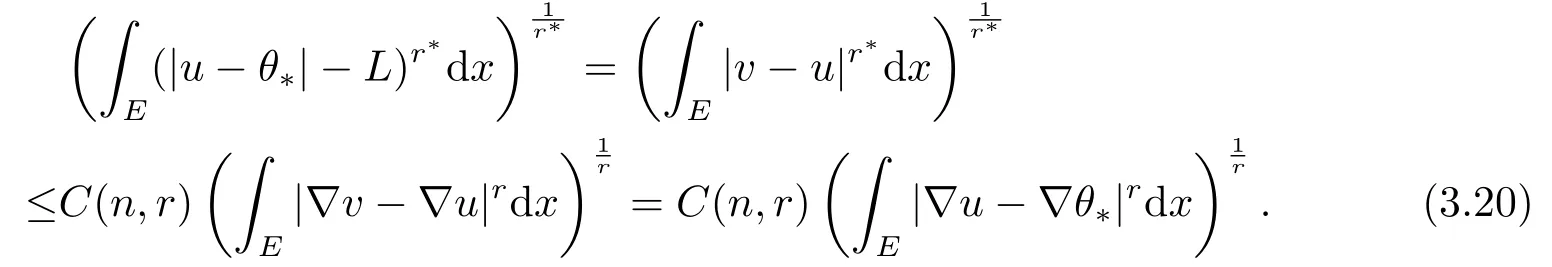
通過整理(3.19)，(3.20)，(3.21) 和E ={|u-θ*|＞L}，得到

其中C*=C*(n，p，q，λ，Λ1，Λ2，δ，|Ω|).于是有

情形(i) 如果1 ≤q ＜n，有β ＜1.在這種情況下，如果s ≥1，由引理2.2可以得到

其中

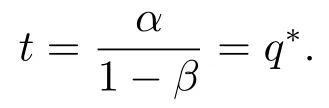
如果0 ＜s ＜1，有

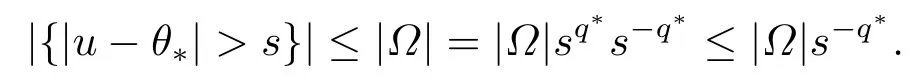
綜上，得到

情形(ii) 如果q =n，有β =1.任意的1 ≤τ ＜∞，由(3.23)知

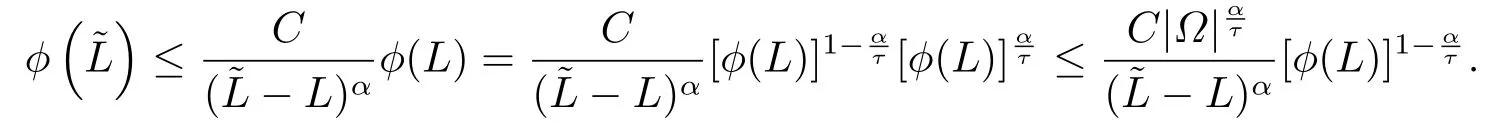
綜上，根據Stampacchia引理得到u ∈θ*+Lτ(Ω).

情形(iii) 如果q ＞n，有β ＞1.引理2.2意味著對某些

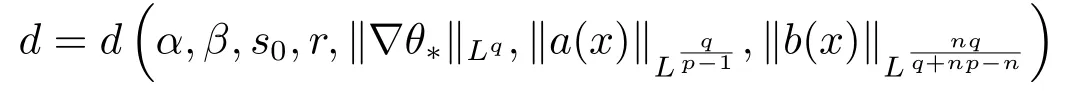
有φ(d)=0.因此|{|u-θ*|＞d}|=0，這里u-θ*≤d在Ω中幾乎處處成立.于是

證明完畢.