具有比例依賴的非自治捕食者-兩互惠食餌系統(tǒng)的動力學行為

艾合麥提·麥麥提阿吉

(新疆大學數(shù)學與系統(tǒng)科學學院，新疆 烏魯木齊830046)

1.引言

在現(xiàn)實世界中，兩個種群之間的相互作用有多種類型，其中捕食-食餌關(guān)系是最常見的生態(tài)相互作用之一.眾所周知，近年來國內(nèi)外諸多學者對種群捕食者-食餌動力系統(tǒng)進行了廣泛的研究，并且研究工作取得了很大的進展.[1-5]到目前為止，在種群捕食者-食餌動力系統(tǒng)研究方面已經(jīng)建立了許多重要且有意義的結(jié)果.其基本和重要的研究問題主要是包括種群的持久性和滅絕性系統(tǒng)正周期解的存在性，全局穩(wěn)定性和全局吸引性等等.值得注意的是，大多數(shù)捕食者-食餌動力系統(tǒng)研究中在描述捕食者及其食餌的動態(tài)相互作用時，總是利用比例依賴函數(shù)(功能反應函數(shù))來描述捕食者的捕食率和轉(zhuǎn)化率.然而，最近有些種群動力學模型方面的研究利用比例依賴函數(shù)來描述種群之間的競爭關(guān)系和互惠關(guān)系(合作關(guān)系)并建立動力學模型[6-13].例如，在文[7]中May首先提出了以下具有比例依賴的兩種群合作系統(tǒng)

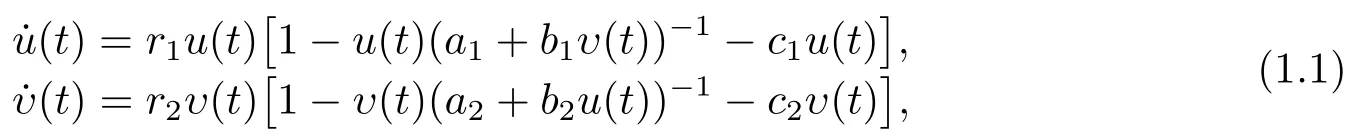
其中u(t)和v(t)表示兩個合作種群u和υ在時刻t的密度;u(t)(a1+b1υ(t))-1和υ(t)(a2+b2u(t))-1描述種群u和種群υ 之間合作關(guān)系.后來這種具有比例依賴的合作系統(tǒng)被稱為May型合作系統(tǒng)[9].文[9-10]在文[7]研究模型的基礎(chǔ)上進一步研究了具有時滯的多種群May型合作系統(tǒng)和具有時滯和擴散的兩種群May型合作系統(tǒng)的動力學行為.另外，最近文[11]研究了以下捕食者-食餌-合作系統(tǒng)

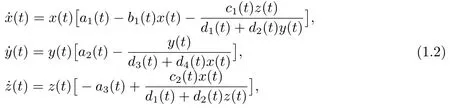
的持久性.其中x(t)和y(t)表示兩個合作食餌種群x和y在時刻t的密度; z(t)表示捕食者種群z在時刻t的密度.在系統(tǒng)(1.2)中作者用來同時描述了捕食者和兩個食餌之間的捕食-食餌-合作關(guān)系.在本文中結(jié)合以上的研究工作和模型，考慮下面的具有比例依賴的非自治捕食者-兩互惠食餌系統(tǒng):

其中x(t)，y(t)分別表示兩互惠食餌種群x和y在時刻t的密度;z(t)表示捕食者種群z在時刻t的密度; ai(t)(i = 1，2，3)是種群x，y和z在時刻t的增長率; bi(t)(i = 1，2，3)分別表示種群x，y和z在時刻t內(nèi)部密度制約項.在系統(tǒng)(1.3)中考慮了一個捕食者和兩個食餌，并且用和來描述了兩個食餌之間的互惠關(guān)系，用來描述捕食者和食餌之間的捕食-食餌關(guān)系.系統(tǒng)(1.3)迄今未曾被研究過，并且目前已研究過的大部分其他比例依賴的捕食者-食餌-合作系統(tǒng)主要研究了模型的持久性，滅絕性和正周期解的存在性，幾乎沒有研究過系統(tǒng)的全局吸引性.因此，本文章將研究系統(tǒng)(1.3)的有界性，持久性，滅絕性，正周期解的存在性以及全局吸引性等動力學行為.

2.預備知識

由系統(tǒng)(1.3)的實際生物意義，我們假設(shè)系統(tǒng)(1.3)滿足下面的初始條件:

(H1) ai(t)，bi(t)(i=1，2，3)，ci(t)，di(t)，ei(t)(i=1，2)和fi(t)(i=1，2)是在區(qū)間[0，+∞)上有界，連續(xù)的正函數(shù).

為了敘述方便，對任意在區(qū)間[0，+∞)上連續(xù)的函數(shù)f(t)，我們用下面的記號

此外，我們還將用到如下一些定義和引理

定義2.1[3]我們稱系統(tǒng)(1.3)是持久的，如果存在正的常數(shù)mi，Mi(i = 1，2，3)和T*使得系統(tǒng)(1.3) 的每個正解(x(t)，y(t)，z(t))對于任何給定初始條件Φ滿足m1≤x(t) ≤M1，m2≤y(t)≤M2，m3≤z(t)≤M3，?t ≥T*，其中T*依賴于Φ.

定義2.2[12]稱系統(tǒng)(1.3)是全局吸引的如果系統(tǒng)(1.3)的任意的兩個解(x(t)，y(t)，z(t))和(u(t)，v(t)，μ(t)) 滿足

引理2.1[12]考慮下面的方程

其中d2＞0，我們有下面的結(jié)論:

1) 如果d1＞0，那么

2) 如果d1＜0，那么=0.

引理2.2[13]若存在正常數(shù)m和M 使得對任何中任Φ ∈[-τ，0]，都有

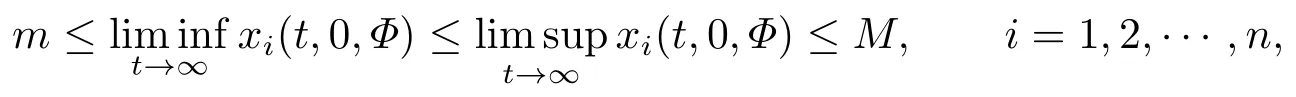
則下面一般形式的泛函微分方程

一定存在周期為ω的正周期解，其中x(t) ∈ Rn而F(t，xt)是n維連續(xù)實泛函，x(t，0，Φ) =(x1(t，0，Φ)，x2(t，0，Φ)，··· ，xn(t，0，Φ)).

引理2.3[14]設(shè)f是定義在[0，∞)上的一個非負函數(shù)使得在[0，∞)上可積并且在[0，∞)上一致連續(xù)，則

3.系統(tǒng)的有界性，持久性以及正周期解的存在性

定理3.1假設(shè)(H1)成立，則系統(tǒng)(1.3)是最終有界的.

證首先，由系統(tǒng)(1.3)的第一個方程對t ≥0我們可以得到，

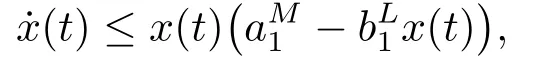
考慮下面的輔助方程

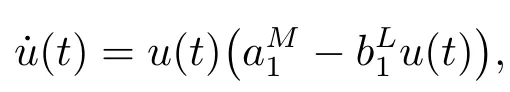
由引理2.1，可以得到

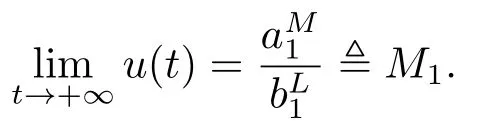
根據(jù)微分方程的比較原理，存在一個常數(shù)T0＞0使得x(t) ≤M1，其中t ≥T0.其次，由系統(tǒng)(1.3)的第二個和第三個方程對t ≥0可以得到，

然后，類似于上面的討論，存在一個常數(shù)T1＞0使得對t ≥T1有y(t)≤M2和z(t)≤M3，其中

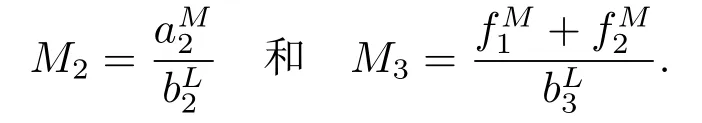
定理3.2假設(shè)(H1)成立并且Ai＞0(i = 1，2)，則存在常數(shù)m1＞0，m2＞0，使得系統(tǒng)(1.3)的任一個正解(x(t)，y(t)，z(t))滿足下面的條件

證由系統(tǒng)(1.3)的第二個和第三個方程對t ≥0可以得到，

定理3.3假設(shè)系統(tǒng)(1.3)滿足定理3.2的全部條件并且滿足A3＞0，則系統(tǒng)(1.3)是持久的，其中

證由定理3.1和定理3.2，存在常數(shù)T4＞0，使得對任意給定的常數(shù)ε0＞0有

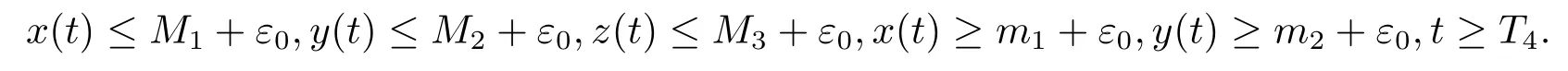
由系統(tǒng)(1.3)的第三個方程得到

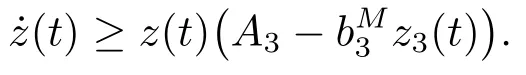
由ε0的任意性且類似于定理3.2中的討論，存在常數(shù)T5＞0，使得對t ≥T5有z(t) ≥m3，其中

故，根據(jù)定義2.1，系統(tǒng)(1.3)是持久的.

由引理2.1 可以得到下面的推論.

推論3.1假設(shè)(H1)成立并且A4＜0，則捕食者種群z滅絕，其中

下面假設(shè)系統(tǒng)(1.3)為周期系統(tǒng)的條件下得到系統(tǒng)至少存在一個正周期解的充分條件.

(H2) ai(t)，bi(t)(i=1，2，3)，ci(t)，di(t)，ei(t)(i=1，2)和fi(t)(i=1，2)都是ω-周期非負連續(xù)函數(shù).

由引理2.2可以得到下面的推論.

推論3.2假設(shè)(H2)成立并且Ai＞0(1，2，3)，則系統(tǒng)(1.3)至少有一個正ω-周期解.

4.系統(tǒng)的全局吸引性

首先，為了方便我們介紹一些記號

其中

關(guān)于系統(tǒng)(1.3)的全局吸引性，我們有下面的結(jié)論.

定理4.1假設(shè)系統(tǒng)(1.3)滿足定理3.3的全部條件并且滿足D ＞0，則對系統(tǒng)(1.3)是全局吸引的.

證設(shè)(x(t)，y(t)，z(t))和(u(t)，v(t)，μ(t))是系統(tǒng)(1.3)的任意兩個正解.由系統(tǒng)(1.3)的持久性，存在常數(shù)T ＞0，mi＞0，Mi＞0(i = 1，2，3)使得m1≤x(t) ≤M1，m2≤y(t) ≤M2，m3≤z(t)≤M3對一切t ≥T成立.定義Liapunov函數(shù)

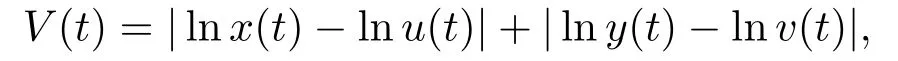
則沿著系統(tǒng)(1.3)計算V(t)的右上導數(shù)，得到

在區(qū)間[T，t]上積分(4.1)，我們得到

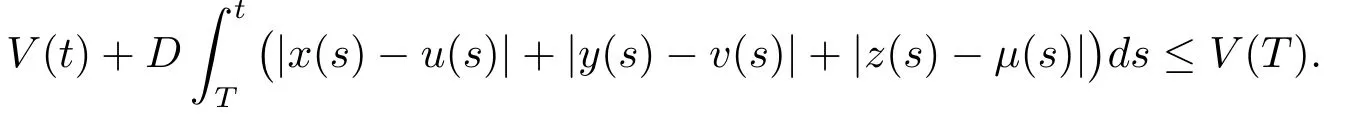
因此，V(t)在區(qū)間[T，∞)上有界，從而得到

由系統(tǒng)(1.3)的持久性和(4.2)我們可以得到|x(s)-u(s)|+|y(s)-v(s)|+|z(s)-μ(s)|和它們的導數(shù)在區(qū)間[T，+∞)上有界的.從而由引理2.3(Barbalat引理)得到

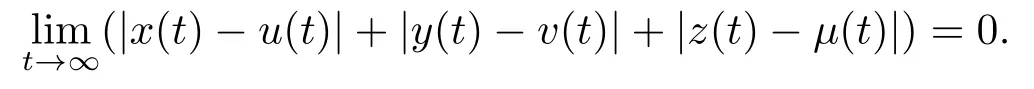
因此，

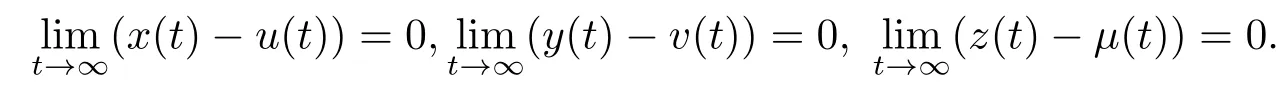
由定理4.1和推論3.2，有下面的結(jié)論

推論4.1假設(shè)條件(H2)成立，且Di＞0(i = 1，2，3)，則系統(tǒng)(1.3)有一個全局吸引的正ω-周期解.