天然食用色素的多元線性模型和神經網絡模型的配色效果比較
劉 亞,雷 聲,朱大洲,高 莉,劉國榮,王成濤,*,劉 娟,郭 青
(1.云南中煙工業有限責任公司 技術中心, 昆明 650202;2.北京工商大學 北京市食品添加劑工程技術研究中心, 北京 100048;3.農業農村部食物與營養發展研究所, 北京 100081)
食品著色劑(食用色素)是食品添加劑的重要門類,廣泛應用于食品、醫藥、化妝品、印染、煙草等工業領域[1-2]。在食品及包裝中應用食用色素,可賦予其鮮艷的顏色,吸引消費者,刺激其視覺、聽覺、嗅覺與味覺,在生理和心理方面影響消費行為[3-7]。近年來,發現多種天然食用色素還具有一定生理活性、保健功能,可作為食品營養強化劑[8-9]。
食用色素呈現出不同的顏色,是其對不同波長的光選擇性吸收的結果。光譜曲線則是以物質的吸光度為依據,反映物質顏色特性的曲線。通常色素的光譜曲線也被稱為色素顏色的“指紋”[3,10]。目前,天然食用色素的調配仍大多依靠人工配色,其高度依賴配色者的配色經驗,受其心理因素、生理因素和其他條件的影響,生產效率低,產品質量穩定性差[11-12]。除人工配色外,計算機配色技術已有一些報道。近年來,基于光譜反射率重建模型建立RGB顏色空間到L*、a*、b*顏色空間的映射方法,用于顏色測量,并通過多元線性回歸模型、神經網絡模型等進行色素調配、織物染色的研究已見報道[13-16]。相關研究表明,采用光譜曲線對天然食用色素建立配色模型,可有效提高配色模型的精確度,減少預測顏色與目標顏色之間的色差[17]。
本文基于天然食用色素的質量濃度與其在特征最大吸收波長下吸光度呈正比關系的原理,利用光譜曲線對顏色描述的唯一性特性[17-18],構建了天然食用色素的2種配色模型。通過分析預測多元線性模型和神經網絡模型對天然食用色素的復配效果,以及對比2種模型的預測性能,選出較優模型,并完成了對較優模型的復配驗證。希望研究結果可以為天然食用色素的配色模型構建、智能配色等提供新的理論依據和技術參數。
1 材料與方法
1.1 材料與儀器
紅曲紅、梔子黃、梔子藍色素,河南中大恒源生物科技股份有限公司。
UV- 3600 Plus型紫外- 可見分光光度計,島津儀器有限公司;CM- 3610A型色差儀,日本柯尼卡美年達公司;BSG- 300型光照培養箱,上海博訊實業有限公司醫療設備廠。
1.2 實驗樣品配制
選擇紅曲紅、梔子黃和梔子藍三原色色素按照一定比例進行復配,得到復配色素溶液,共計156組樣品,其制備配比見表1,其中樣品1-31為單一色素溶液,樣品32-156為復配色素溶液。
1.3 樣品色素溶液的特征吸收光譜及顏色參數分析
1.3.1色素溶液的特征吸收光譜分析
紫外- 可見分光光度計于350~720 nm波長內,測定表1樣品溶液的可見光吸收光譜,每樣品測量3次,取其平均值進行訓練和優化模型[18]。
1.3.2單色及復配色素溶液的顏色參數測定
選用孔徑9 mm、100% UV、D65光源、10°視角時,全自動色差儀檢測表1中156組樣品溶液的亮度CIEL*(L*)、紅值(a*)和黃值(b*),以超純水為空白,每個樣品檢測3次,取其平均值[17-18]。
1.4 數學模型的選擇
1.4.1多元線性回歸模型
多元線性回歸模型[14]可用于描述因變量y與多個自變量x1,x2,……xn之間的線性相關關系,模型見式(1)。
(1)
式(1)中,x1,x2,…,xk(k≥2)為回歸因子;y為觀測值;b0,b1,b2,…,bk為回歸系數;ε~N(0,σ2)為隨機誤差。
1.4.2神經網絡模型
神經網絡在近紅外光譜分析中得到廣泛應用,其主要由信號的正向傳播和誤差的反向傳播組成[15-16]。正向傳播時,光譜數據從輸入層傳入,經隱含層處理后傳向輸出層,若實際輸出與期望輸出的誤差較大,此時將誤差反向傳播,以修改各個神經單元的權值和閾值,直到網絡的輸出誤差減小到規定范圍,或達到設定的學習次數為止。
1.5 色價計算
在GB/T 5525—2008[19]中2.2節重鉻酸鉀溶液比色法基礎上修改。準確稱取0.1 g試樣,于100 mL容量瓶中用適當溶劑稀釋,用溶劑作參比液于1 cm比色皿中,并用紫外可見分光光度計于最大波長處測定其吸光度,然后計算單一色素的色價,見式 (2)。
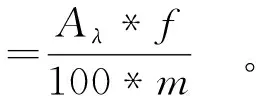
(2)
式(2)中,Aλ為實測試樣在樣品的最大吸收波長λ下的吸光度;f為稀釋倍數;m為試樣質量。
1.6 色差計算
根據CIELAB色差公式,計算色素溶液的色差,見式(3)。
(3)
式(3)中,ΔL*是指實際配方和預測配方溶液亮度的差值;Δa*是指實際配方和預測配方溶液紅值的差值;Δb*是指實際配方和預測配方溶液黃值的差值。
1.7 模型精確度的評價
為更加直觀評價預測模型的精確度,采用平均絕對誤差(MAE)、平均相對誤差(MAPE)、均方誤差(MSE)和均方根誤差(RMSE)等4項指標,對模型的性能進行評估,見式(4)~式(7)。
(4)
(5)
(6)
(7)
式(4)~式(7)中,Yi表示實際值;Y′表示模型預測值;i=1, 2, 3,……n;n為數據量個數。
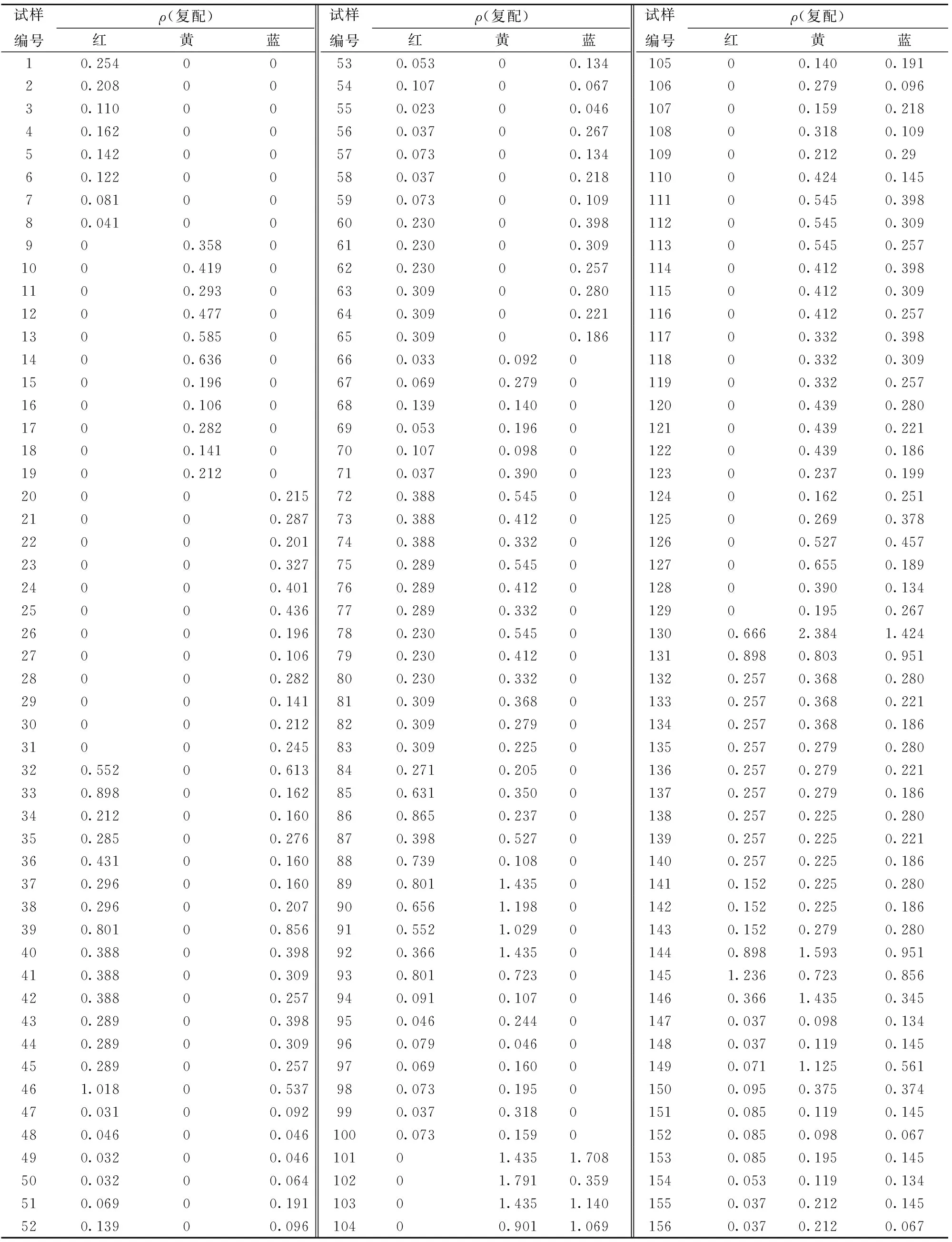
表1 不同質量濃度三原色色素的樣品制備配比Tab.1 Sample preparation proportion of trichromatic pigments with different concentration g·L-1
2 結果與討論
2.1 3種三原色色素的吸收光譜分析
于350~720 nm波長內繪制分析紅曲紅、梔子黃和梔子藍色素的吸收光譜曲線(見圖1),確認單一色素的最大特征吸收峰,發現其最大特征吸收波長分別為442、485、596 nm。根據單一色素溶液樣品1-31的光譜曲線數據,采用式(2)計算得到紅曲紅、梔子黃和梔子藍色素的色價分別為95.33、20.90和30.13。
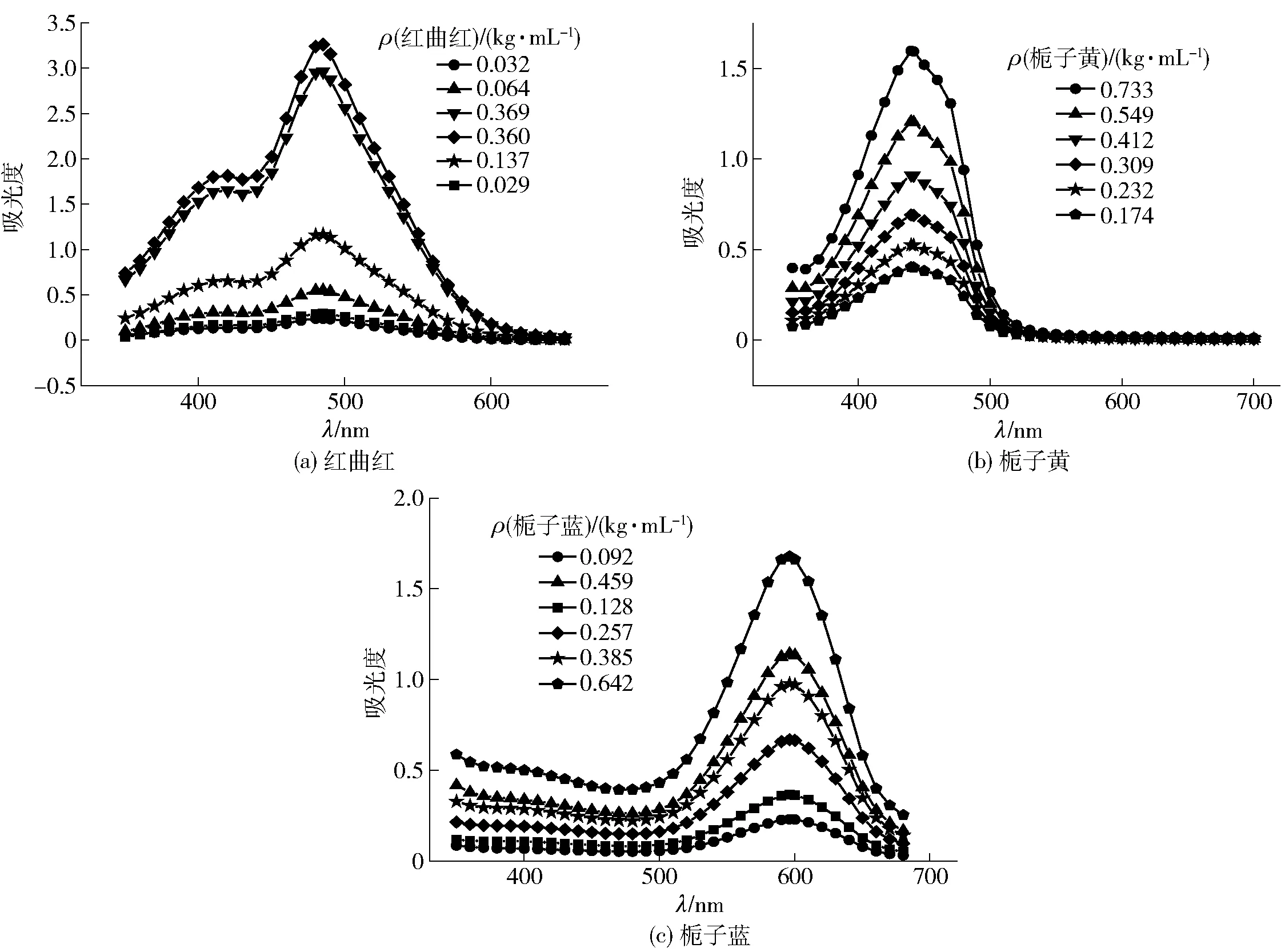
圖1 不同質量濃度紅曲紅、梔子黃、梔子藍色素的吸收光譜Fig.1 Absorption spectral analysis of different concentrations of monascus red pigment, gardenia yellow pigment and gardenia blue pigment
由圖1可知,紅曲紅、梔子黃和梔子藍色素樣品溶液的吸光度與其質量濃度呈正比,隨著色素質量濃度的增加,樣品的吸光度也隨之增加。因此,可通過色素質量濃度與色價相乘得積,計算得到3種單一色素的吸光濃度,用于構建預測模型。
2.2 3種色素復配溶液的吸收光譜分析
按照不同質量比,對紅曲紅、梔子黃和梔子藍3種色素進行復配,于350~720 nm測定復配色素溶液的吸收光譜,并繪制其吸收光譜曲線(見圖2),發現復配色素溶液分別于442、485、596 nm呈現特征吸收峰,與單一色素的最大特征吸收峰基本一致,且3個特征吸收峰下的色素質量濃度與其吸光度呈正相關性。此結果進一步驗證了光譜曲線對顏色描述的唯一性[12,17]。
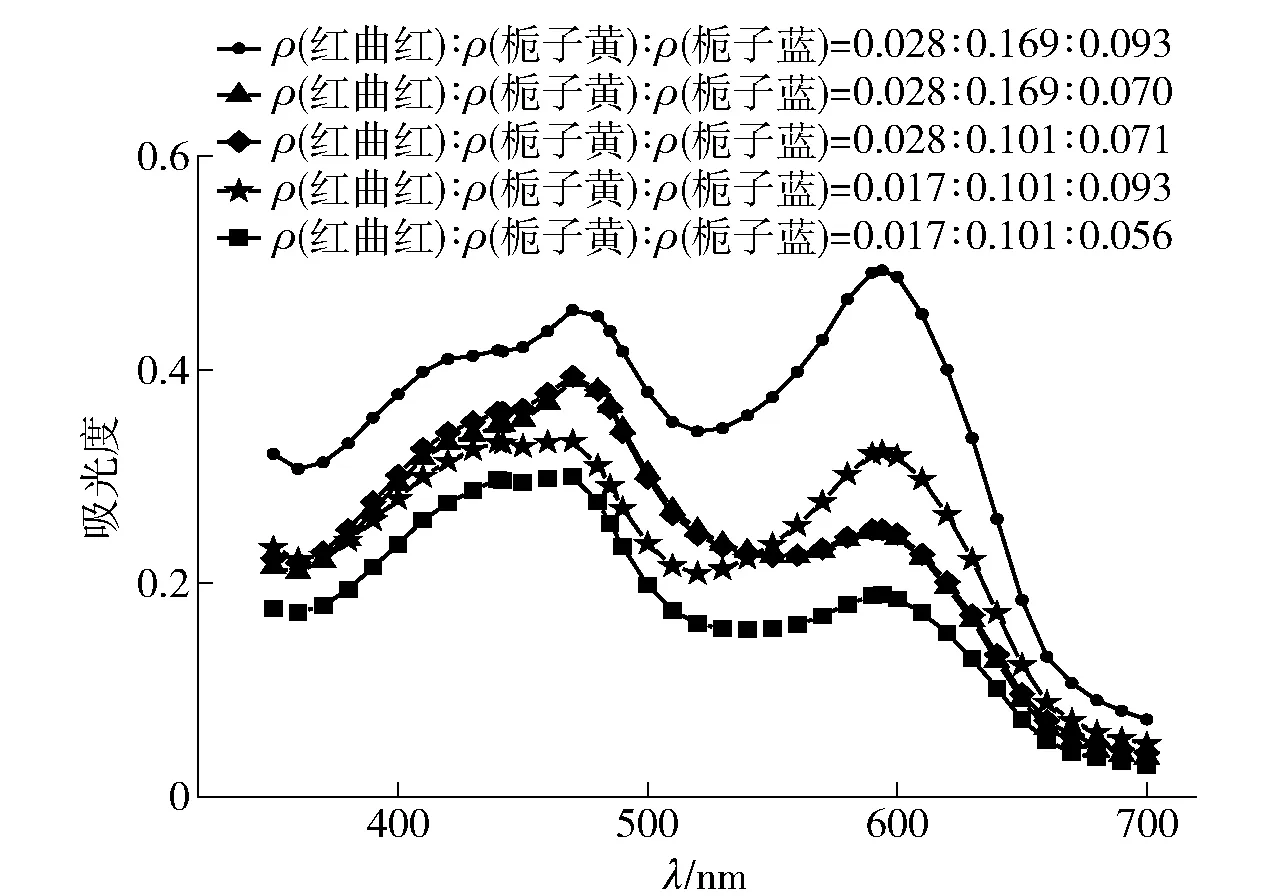
圖2 不同質量濃度三原色色素復配溶液的吸收光譜Fig.2 Absorption spectral analysis of different compound concentrations of trichromatic pigments
2.3 預測模型的構建
根據圖1(單一色素)和圖2(復配色素)的吸收光譜,為適應色素復配的不同色價需求,擴大預測復配模型的適應性,以混合色素溶液在3個特征吸收波長的吸光度為自變量,混合色素溶液內單一色素溶液的色價質量濃度為因變量,構建多元線性和神經網絡預測模型,并分析比較2個預測模型的適應性。
2.3.1多元線性預測模型構建
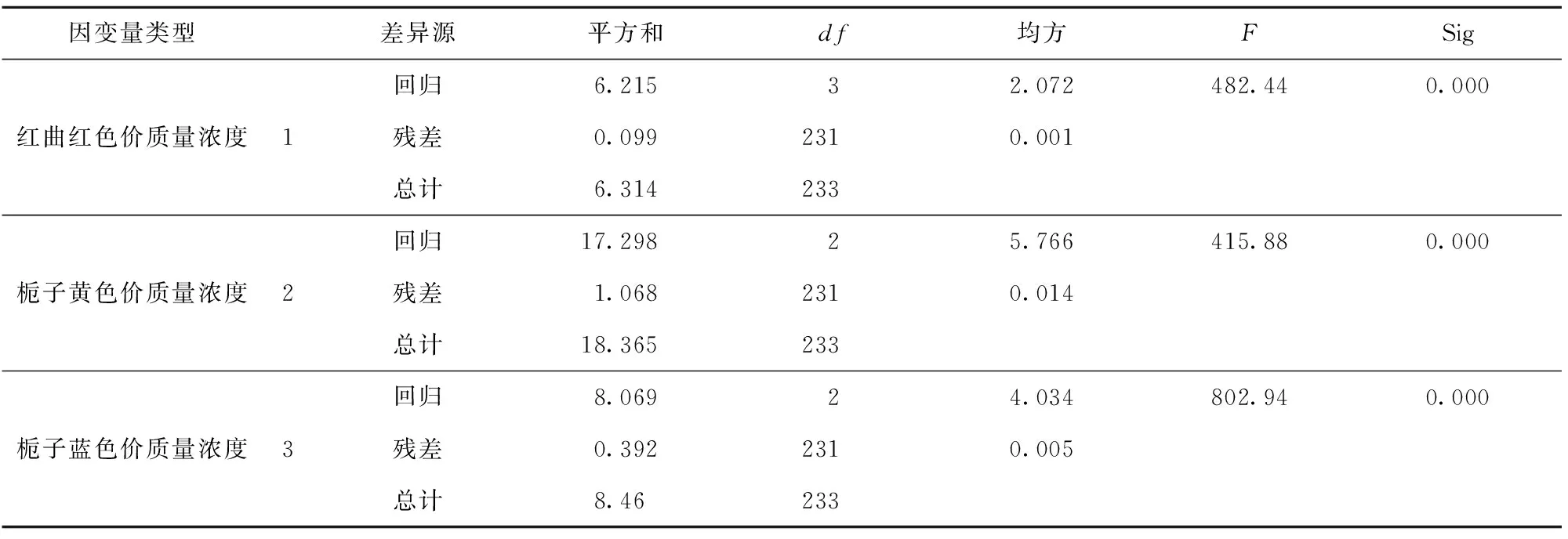
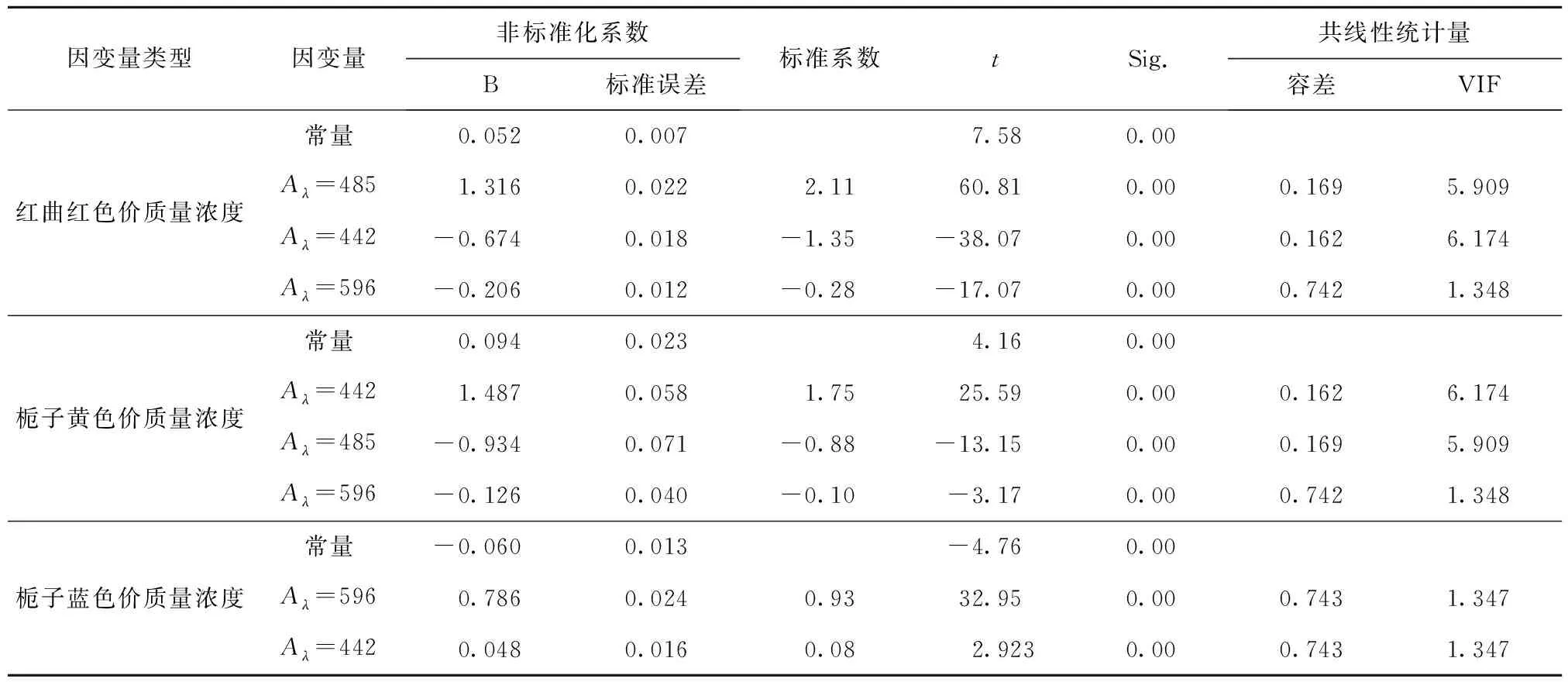
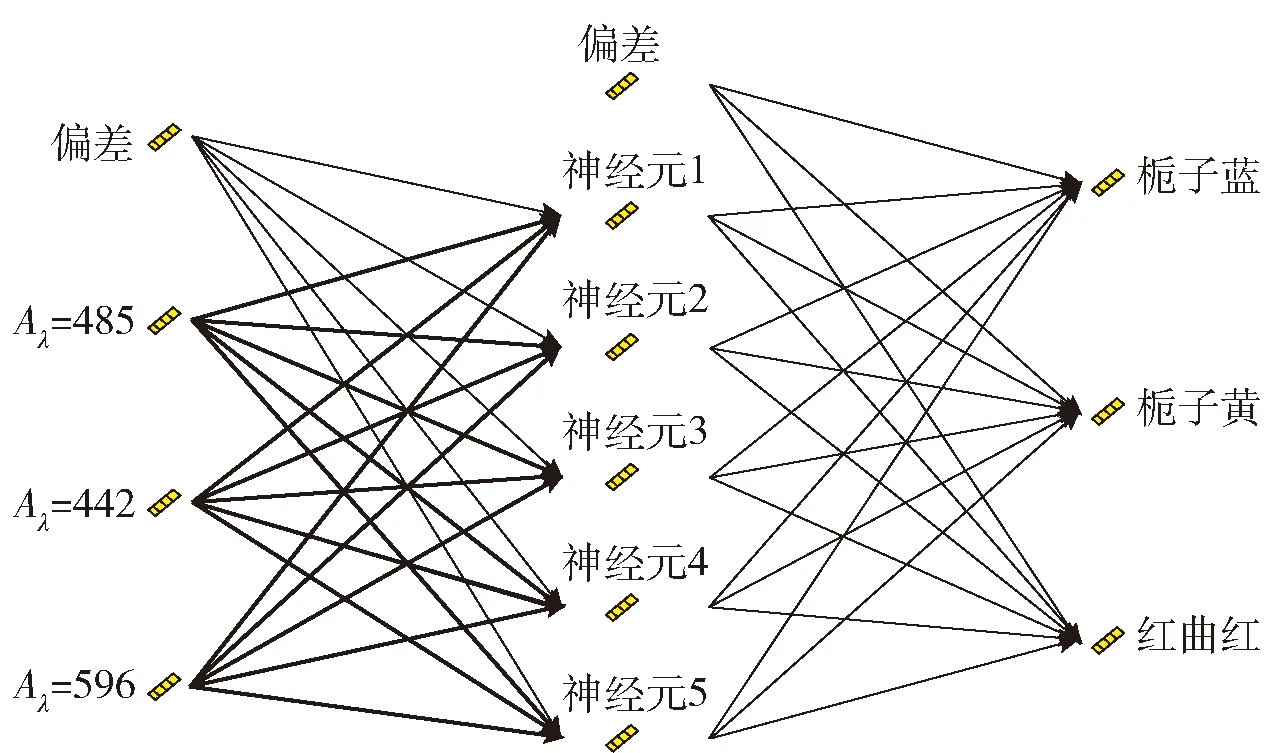
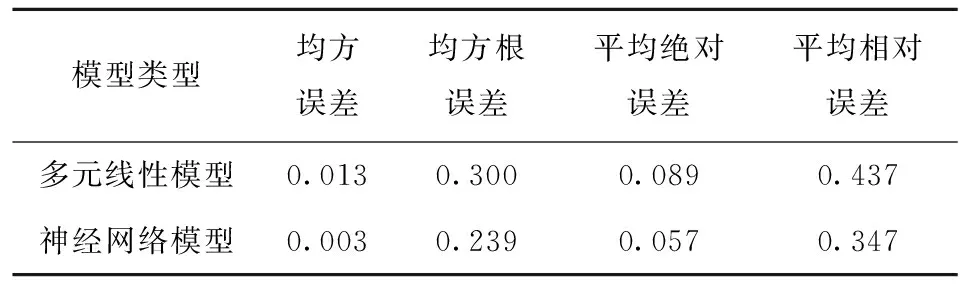
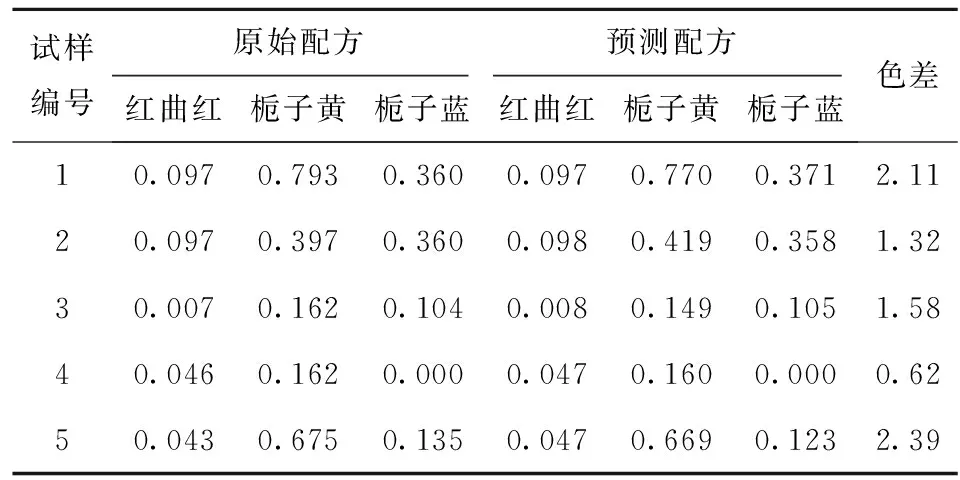
由于不能明確各影響因素對混合色素溶液特征吸收值的影響是否顯著,為建立最優回歸模型,采用逐步回歸方法,對各變量進行F檢驗,使用F值判定回歸模型的變量參數,設置步進方法的F值為:0.05 根據得到的多元線性擬合結果,得到變量移入移除表和模型擬合度檢驗表(見表2),根據R2判定回歸方程的擬合度,優化得到最優擬合方程。由表2中紅曲紅、梔子黃和梔子藍色價質量濃度為因變量,得到優化擬合方程的R2分別為0.992、0.971、0.977,調整后的R2為0.984、0.942、0.954,R2滿足要求,且較接近1,說明構建的回歸方程擬合度良好。這與丁海霞[14]的多元線性回歸模型分析織物染色配色結果相一致。 根據前述優化后擬合方程,通過方差分析得到F值和顯著性結果(見表3)。以紅曲紅、梔子黃和梔子藍色價質量濃度為目標值的回歸模型F值分別為482.44、415.88、802.94,P值均為0.000,說明建立的回歸擬合模型具有統計學上的顯著性,回歸效果有效,回歸方程擬合良好。SPSS軟件模型處理得到的回歸系數(見表4),系數的共線性統計量中,模型的容忍度均大于0.1,VIF(方差膨脹系數)均小于10,表明該模型不存在多重共線性。 2.3.2多層前饋BP神經網絡模型構建 采用IBM SPSS Modeler構建神經網絡模型(見圖3),將442、485、596 nm的復配色素溶液吸光度設置為神經網絡模型輸入層,將紅曲紅、梔子黃、梔子藍色價質量濃度為神經網絡模型輸出層,創建標準模型,選擇建立多層感知器的神經網絡模型,隱藏層數為1個,隱藏層節點為軟件自動計算,以不能進一步降低誤差為中止規則,將數據以7∶3分為訓練區、測試區。隱含層和輸出層的傳遞函數分別為tanh函數,學習速率取0.05,訓練目標為0.001,最大迭代次數為1 000,訓練的誤差精度為0.05。通過軟件的多次迭代計算,最終確定當神經網絡模型的隱藏層神經元為5個時,準確度和運行時間較佳,R2為0.957。 表2 多元回歸分析模型擬合度檢驗和變量移入表Tab.2 Fitting degree inspection and variable value of multiple regression analysis model 表3 方差分析Tab.3 Analysis of variance 表4 多元回歸系數Tab.4 Coefficients of multiple regression 圖3 BP神經網絡模型Fig.3 BP neural network model 構建的多元線性回歸模型和神經網絡模型,對預測驗證區的156組數據進行預測紅曲紅、梔子黃、梔子藍色素色價質量濃度。根據模型結果,通過計算多元線性模型和神經網絡模型的平均絕對誤差(MAE)、平均相對誤差(MAPE)、均方誤差(MSE)和均方根誤差(RMSE)等4項指標評價模型的精確度(見表5),表明神經網絡模型的各個誤差指標均小于多元線性回歸擬合模型,說明神經網絡模型精度較高,且相比于多元線性回歸模型較穩定。因此,采用BP神經網絡模型作為天然色素的復配模型,該結果與對橄欖油中二元、三元混合物的擬合結果相一致[20-21]。 表5 模型預測性能對比Tab.5 Comparison of model predictive ability 采用神經網絡模型進行復配模型的驗證,從樣品制備表中隨機選擇5個色素復配配方,根據獲得樣品的光譜吸收曲線;通過模型預測計算得到預測配方,使用全自動色差儀分別測量原配方和擬合配方獲得的顏色(色調)參數;根據CIELAB色差公式[見式(3)],計算兩者的色差(見表6)。由表6可知,根據神經網絡模型計算得到預測配方與原配方溶液的平均色差為1.604,肉眼無法分辨兩者的差別。 表6 原配方與擬合配方的色差比較Tab.6 Comparison of color aberration between sampleformula and fitting formula 本文分別測定了紅曲紅、梔子黃和梔子藍單一色素溶液及3種色素復配溶液的吸收光譜,通過分析吸收光譜發現,復配色素溶液的特征吸收峰與參與復配的單一色素的最大特征吸收峰基本一致,且色素溶液的質量濃度與其吸光度呈正比。根據色素復配溶液的特征吸收峰吸光度及其復配比例,構建了多元線性回歸模型和神經網絡模型,通過模型誤差分析,表明神經網絡模型相較于多元線性模型具有更高的精度和穩定性,神經網絡模型適用于天然色素復配模型構建。通過試驗驗證得出,預測配方和原配方溶液的色差在3以內,肉眼無法區分兩者的差別,表明使用該配色模型對天然食用色素溶液配色精確度、重復性良好,可以較好地滿足實際生產及應用的需要。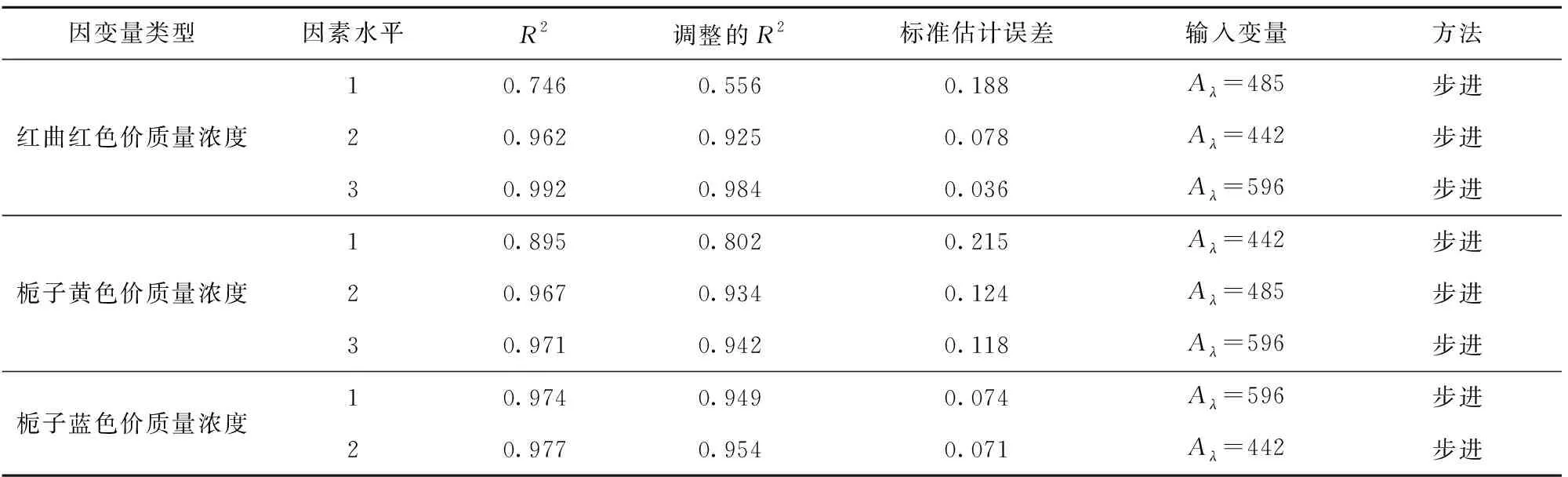
2.4 2種模型的對比分析
2.5 復配模型驗證
3 結 論

