半無限封閉含水層非穩定滲流的“浸潤鋒面”最大距離研究

劉 茂，郭 華，王雙峰，張 鵬

(四川省地質工程勘察院集團有限公司，四川 成都 610072)

半無限單一均質土層的滲流問題研究的較多，現階段理論也較成熟，但是對于半無限封閉含水層的滲流問題相對研究的較少，且大部分都是研究壩體的滲流問題。毛昶熙等[1]基于堤身浸潤線呈斜直線向前推進的假定，推導了不透水地基和透水地基(雙層和多層)上的堤防非穩定滲流浸濕距離L的簡化計算公式，但此公式中采用的補給系數受多種影響因素的影響；吳世余[2]推導了雙層地基(下為砂層、上為黏性土的覆蓋層)的非穩定滲流方程及在特殊條件下的解析解；我國《堤防工程設計規范》[3](GB 50286—2013)假設浸潤線鋒面近似呈直線狀，推導了不透水層地基浸潤線鋒面t時刻的最大距離公式；針對透水地基的浸潤線鋒面研究較少，且理論也不成熟，謝斯塔克夫假定上游斜體的滲流全部垂直下滲進入到地基(透水層)而給出了滲流量的計算式，但與實際情況誤差較大[4]，王韋等[5]假定上游斜體有部分滲流進入地基(透水層)給出滲流量的計算式，前人研究都是圍繞著滲流量進行研究，缺乏對壩體浸潤線鋒面的相關研究，對透水層地基的浸潤線鋒面的研究鮮見報道。

前人關于透水地基壩體的相關滲流研究的較多，且大多為穩定滲流問題，還有主要是針對滲流量進行研究，浸潤鋒面研究的更少，且沒有很好的簡易公式，本文借鑒透水地基均質壩體結構思想，參考岸坡的雙元結構，提出了“半無限封閉含水層結構”的概念，即：上為半透水層(黏性土)下為透水含水層(粉砂層)的地質結構被河流切割而形成。隨著計算機的發展，數值法在地下水分析中被廣泛使用，本文采用數值法進行非穩定滲流的研究，數值法主要包括有限差分法、有限元法、邊界元法、離散元法和流形元法等[6-7].本文利用Autobank有限元程序，采用二維滲流理論和相關的有限元理論，借鑒壩體滲流研究中的“浸潤鋒面”概念，針對半無限封閉含水層非穩定滲流的浸潤鋒面最大距離的影響因素進行了一系列的研究，為具有該結構岸坡的滲流規律提供一定的參考意義，為控制岸坡滲流提供一定依據。

1 理 論

1.1 滲流理論

二維滲流的一般控制微分方程為[8]：

(1)

式中：H總為總水頭；Kx為x方向的滲透系數；Ky為y方向的滲透系數；Q為施加的邊界流量；θ為單位體積含水率；t為時間。

對于有自由面的非穩定滲流，可采用平均滲流水深H的方式，即：由于微元流量流入流出差額使自由水面升降的水的體積平均分配于高度H上，得到以給水度表達的二維滲流控制微分方程，即為Boussinesq方程[9-10]，具體方程如下：

(2)

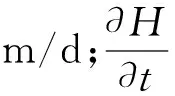
給水度除與滲透系數密切相關外，還與土的緊密度和介質的幾何性質有關[4，11]，本文給水度計算采用南京水利科研院的給水度公式，公式為：

μ=1.137n(0.0001175)0.067(6+lgk)

(3)

式中:μ為給水度，或含水層的自由孔隙率；k為滲透系數,m/d；n為體積孔隙率。

1.2 有限元理論

對控制方程應用加權余量的伽遼金方法，可以得到二維滲流的有限元方程[8,12]：

(4)

式中:[B]為梯度矩陣；[C]為單元滲透系數矩陣；[H]為節點水頭矩陣；〈N〉為插值函數向量；q為穿過單元邊界的單元流量；τ為單元厚度；t為時間；λ為存儲項，對瞬態順流等于mwγw；A為在單元面積上的求和符號；L為在單元邊界長度上的求和符號。

2 模型建立

假設條件：① 各含水層均質、各向同性、土層水平且側向無限延伸; ② 滲流為二維流且服從達西定律；③ 河水位上升為瞬時完成，不考慮入滲補給；④ 初始潛水位與河道的初水位(h0)水平[13]；⑤ 滲流模型底部透水性可忽略不計(或者采取很小的值)。

依據以上假設條件，具體模型如圖1所示。

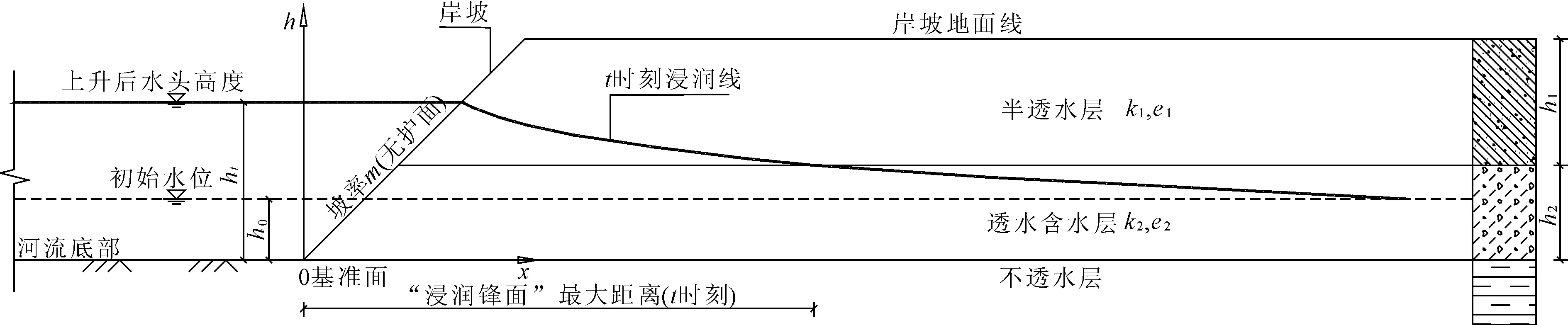
圖1 河道切割形成的半無限密閉含水層結構

鑒于三角形單元能較好地適應滲流場復雜的邊界形狀和非均質土層分布，因此，單元采用常用的三角形單元，本文模型劃分的網格密度為3.03，基本上能滿足模型的精度要求。

3 浸潤鋒面最大距離影響因素分析

3.1 滲透系數的影響

本滲流模型采用直立岸坡，含水層滲透系數k2分別取0.002 m/s，0.004 m/s和0.006 m/s，孔隙率e2=0.335，相對弱透水層滲透系數k1分別為0.000 04 m/s、0.000 08 m/s、0.000 16 m/s、0.000 40 m/s、0.000 80 m/s，孔隙率e1=0.395，初始水位為12 m，瞬時上升的水頭為28 m，計算的非穩定滲流浸潤鋒面距離見圖2和圖3。

圖2 不同持續時間的浸潤鋒面最大距離與滲透系數k1關系曲線

由圖2可知，短時間滲透，隨著上部半透水層的滲透系數增大呈凹曲線型式，上部半透水層滲透系數越小下降越快，隨著滲透系數增大，浸潤鋒面最大距離呈近直線增長，且斜率越來越大；較長時間滲透，隨著上部半透水層的滲透系數增大基本上呈線性增長趨勢(滲透系數極小的除外)；隨著下部透水層滲透系數的增大，凹曲線下降部分的歷時越來越短。

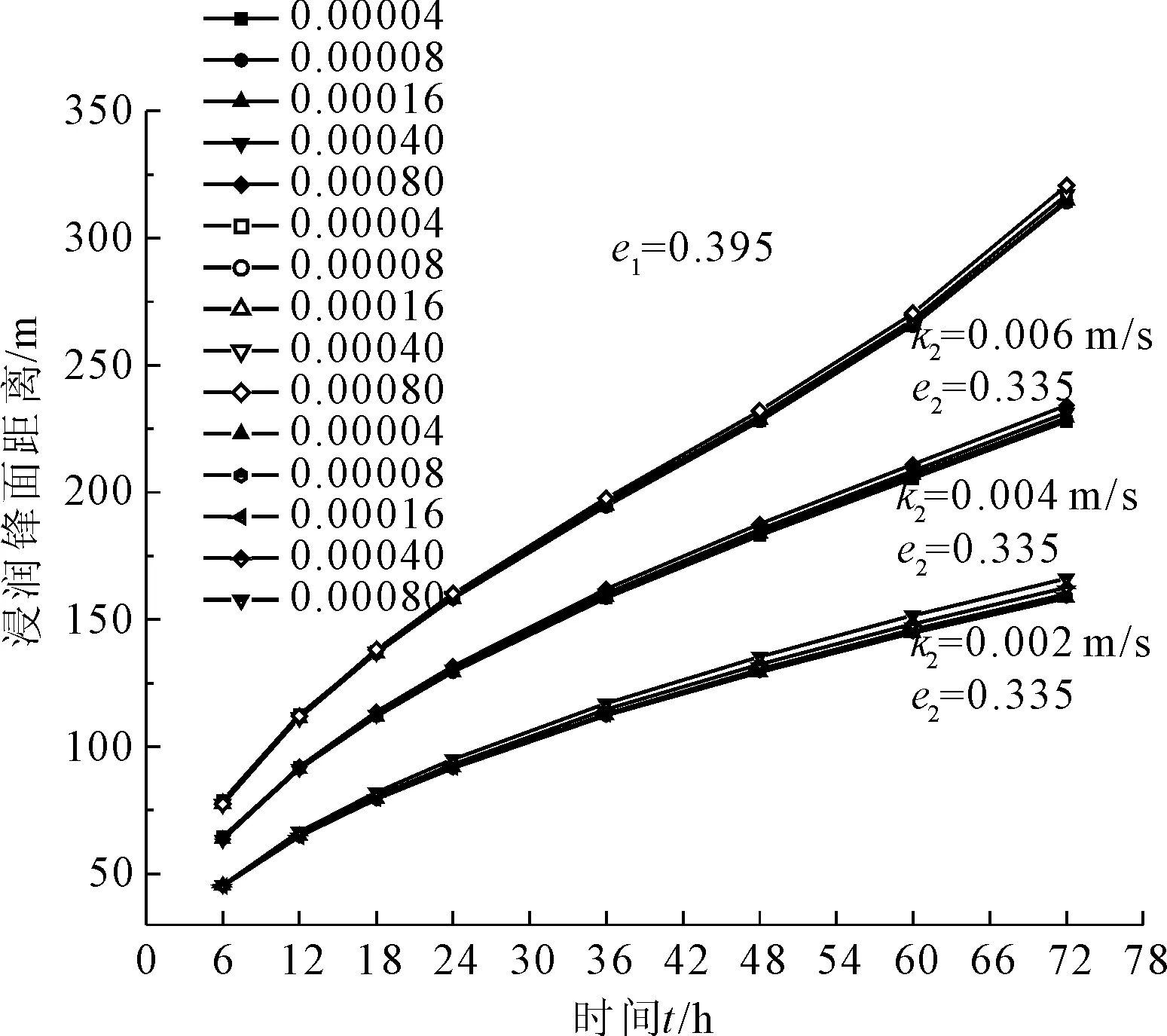
圖3 不同滲透系數的浸潤鋒面最大距離隨滲流時間關系曲線

由圖3可知，浸潤鋒面最大距離受下部透水層的滲透系數控制，受上部半透水層的滲透系數影響很小。短時間滲透，浸潤鋒面最大距離隨下部透水層滲透系數增大呈減速增長趨勢，長時間滲透，浸潤鋒面最大距離隨下部透水層滲透系數增大呈指數趨勢增長，短時間和長時間滲透的界定時間為60 h。

3.2 透水含水層厚度的影響

本滲流模型采用直立岸坡，透水含水層滲透系數k2=0.004 m/s，孔隙率e2=0.335，相對弱透水層滲透系數k1=0.000 04 m/s，孔隙率e1=0.395，初始水位為12 m，瞬時上升的水頭為28 m，含水層厚度取0.5 m～20.0 m，計算的非穩定滲流浸潤鋒面距離見圖4、圖5和圖6。

由圖4可知，浸潤鋒面最大距離隨透水含水層厚度增厚呈現先增大再減小最后趨于線性增長的趨勢。

初始水位低于下部透水層底面時，下部透水層厚度小于等于初始水位與透水層頂的距離的一半時，浸潤鋒面最大距離隨土層厚度呈上凸冪函數增長。下部透水層厚度大于初始水位與透水層頂距離一半的1/2～3/4時，滲流時間小于24 h時，隨著下部透水層厚度增大，浸潤鋒面最大距離減小，滲流時間大于24 h時，隨著下部透水層厚度增大，浸潤鋒面最大距離呈現先減小再增大趨勢，下部透水層厚度為初始水位與透水層頂距離一半的3/4～1時，浸潤鋒面最大距離呈近直線下降，且下降的速率隨著滲流時間增長而增大。

初始水位高于下部透水層底面時，隨著下部透水層厚度的增大，浸潤鋒面最大距離呈近線性增長，且隨著滲透時間推移，增長速率增大。

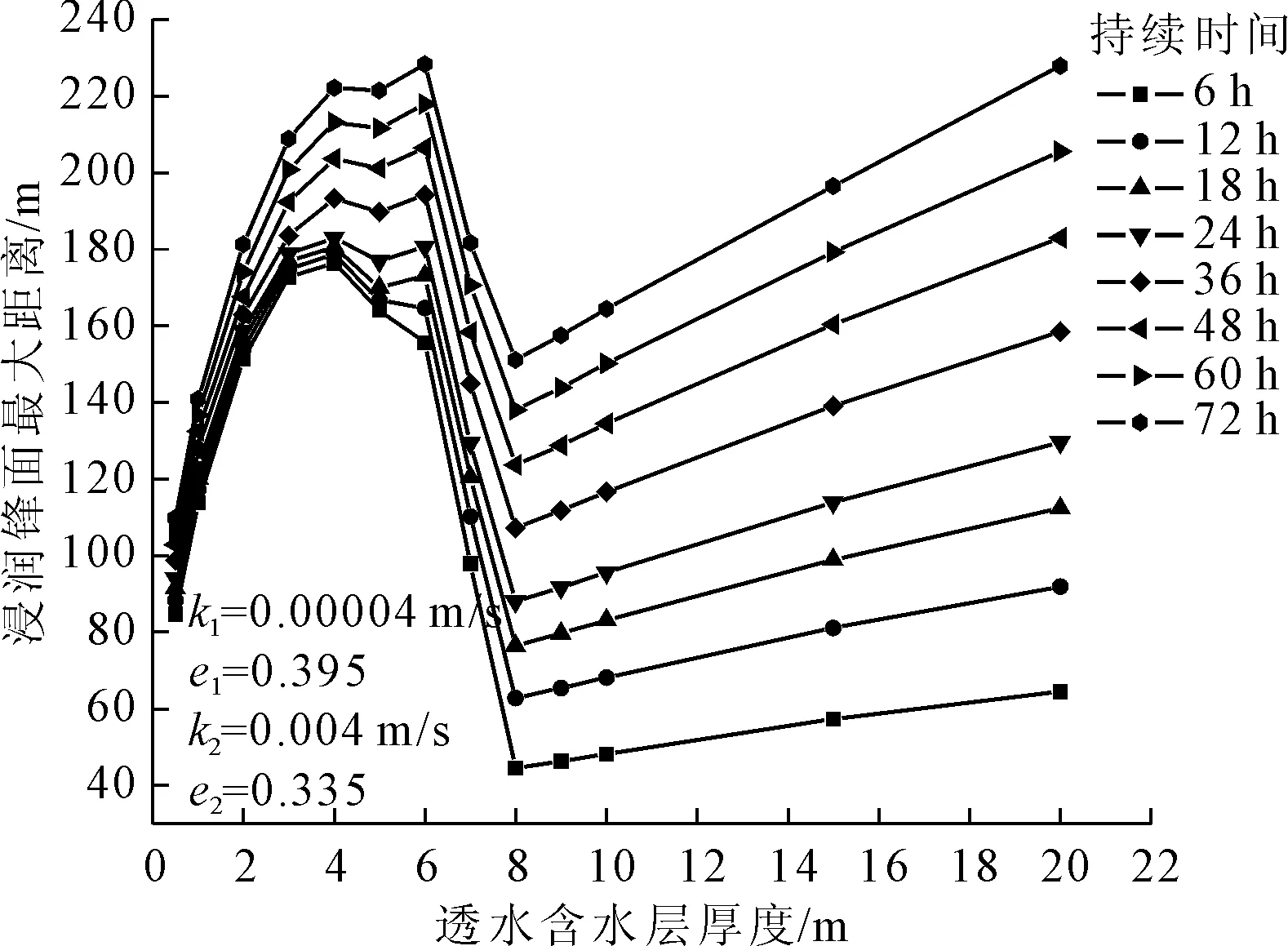
圖4 不同持續時間的浸潤鋒面最大距離與含水層厚度關系曲線

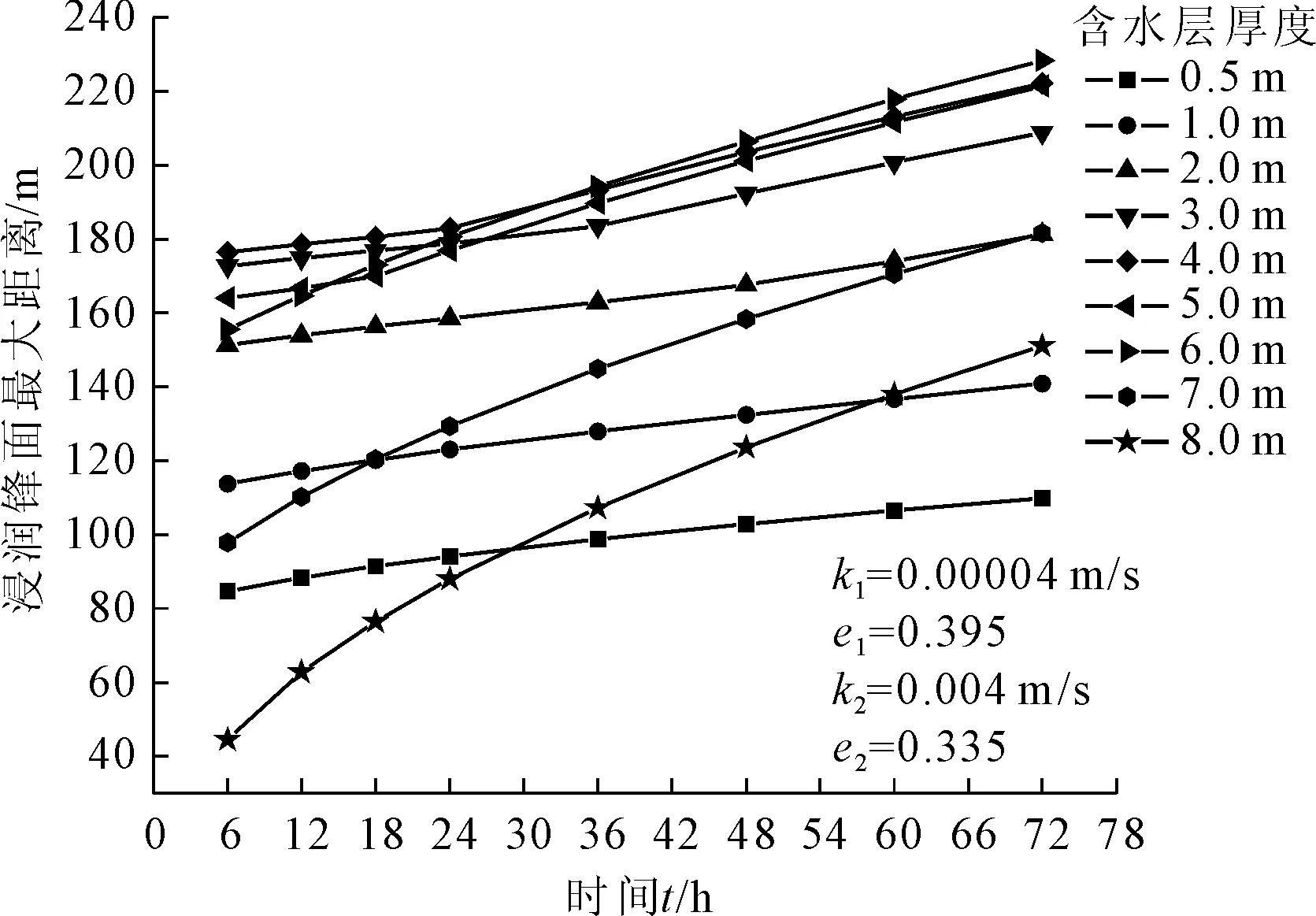
圖5 不同含水層厚度的浸潤鋒面最大距離與滲流時間關系曲線(初始水位低于下部透水層底面)

由圖5可知，初始水位低于下部透水層底面時，滲流時間小于24 h時，浸潤鋒面最大距離為下部透水層厚度等于初始水位與透水層頂的距離的一半；滲流時間大于24 h時，浸潤鋒面最大距離為下部透水層厚度等于初始水位與透水層頂的距離的3/4處。

下部透水層厚度小于等于初始水位與透水層頂的距離的一半時，浸潤鋒面最大距離隨土層厚度增大呈近線性增長；下部透水層厚度大于初始水位與透水層頂的距離的一半時，浸潤鋒面最大距離隨土層厚度增大呈上凸冪函數趨勢增長。

由圖6可知，初始水位高于下部透水層底面時，隨著滲透時間的推移，浸潤鋒面最大距離呈上凸冪函數趨勢增長，下部透水層厚度越厚，浸潤鋒面最大距離增長速率增大。

圖6 不同含水層厚度的浸潤鋒面最大距離與滲流時間關系曲線(初始水位高于下部透水層底面)

3.3 初始水位在透水層位置的影響

本模型采用直立岸坡，透水含水層厚度為20 m，含水層滲透系數k2=0.004 m/s，孔隙率e2=0.335，相對弱透水層滲透系數k1=0.000 04 m/s，孔隙率e1=0.395。初始水位分別取12 m、13 m、14 m、15 m、16 m、17 m、18 m，瞬時上升的水頭高度為28 m，計算的非穩定滲流浸潤鋒面距離見圖7和圖8。

圖7 不同持續時間的浸潤鋒面最大距離與初始水位關系曲線

由圖7可知，浸潤鋒面最大距離隨位于透水含水層的初始水位增高呈指數增長趨勢，且滲流時間越長，浸潤鋒面最大距離增長越慢。

由圖8可知，浸潤鋒面最大距離隨滲流時間呈上凸冪曲線增長，且隨著水頭的增高，浸潤鋒面最大距離增長越快。

3.4 斜坡坡率的影響

本模型采用傾斜岸坡，透水含水層滲透系數k2=0.004 m/s，孔隙率e2=0.335，相對弱透水層滲透系數k1=0.000 04 m/s，孔隙率e1=0.395，初始水位分別取12 m，瞬時上升的水頭高度為28 m，傾斜岸坡坡率分別為0.00、0.25、0.50、0.75、1.00，計算的非穩定滲流浸潤鋒面距離見圖9和圖10。

圖8 不同初始水位的浸潤鋒面最大距離與滲流時間關系曲線

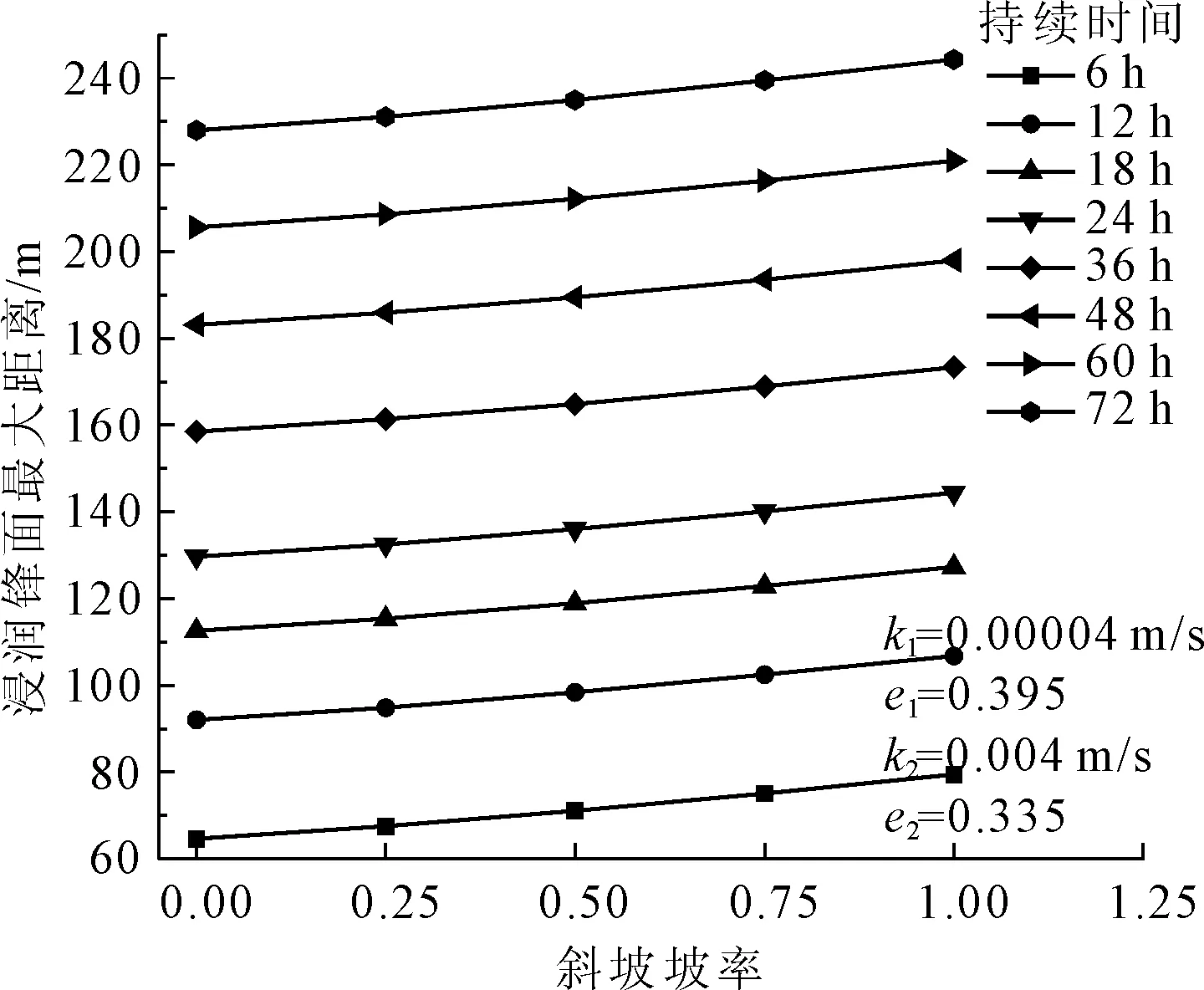
圖9 不同持續時間的浸潤鋒面最大距離與岸坡坡率關系曲線

由圖9可知，浸潤鋒面最大距離受斜坡坡率影響較大，隨著岸坡斜率的增大呈近線性增長，且增長的斜率基本不隨滲透時間變化。

圖10 不同岸坡坡率的浸潤鋒面最大距離與滲流時間關系曲線

由圖10可知，浸潤鋒面最大距離隨著滲流時間增長，基本呈上凸冪函數曲線增長，曲線形狀基本不受斜坡坡率影響，但隨著斜率增大而增大，增大的幅度基本一致。

3.5 水頭高度的影響

本模型采用直立岸坡，透水含水層滲透系數k2=0.004m/s，孔隙率e2=0.335，相對弱透水層滲透系數k1=0.000 04 m/s，孔隙率e1=0.395，初始水位分別取12 m，瞬時上升的水頭高度分別為21 m、22 m、23 m、24 m、25 m、26 m、27 m、28 m，計算的非穩定滲流浸潤鋒面距離見圖11和圖12。

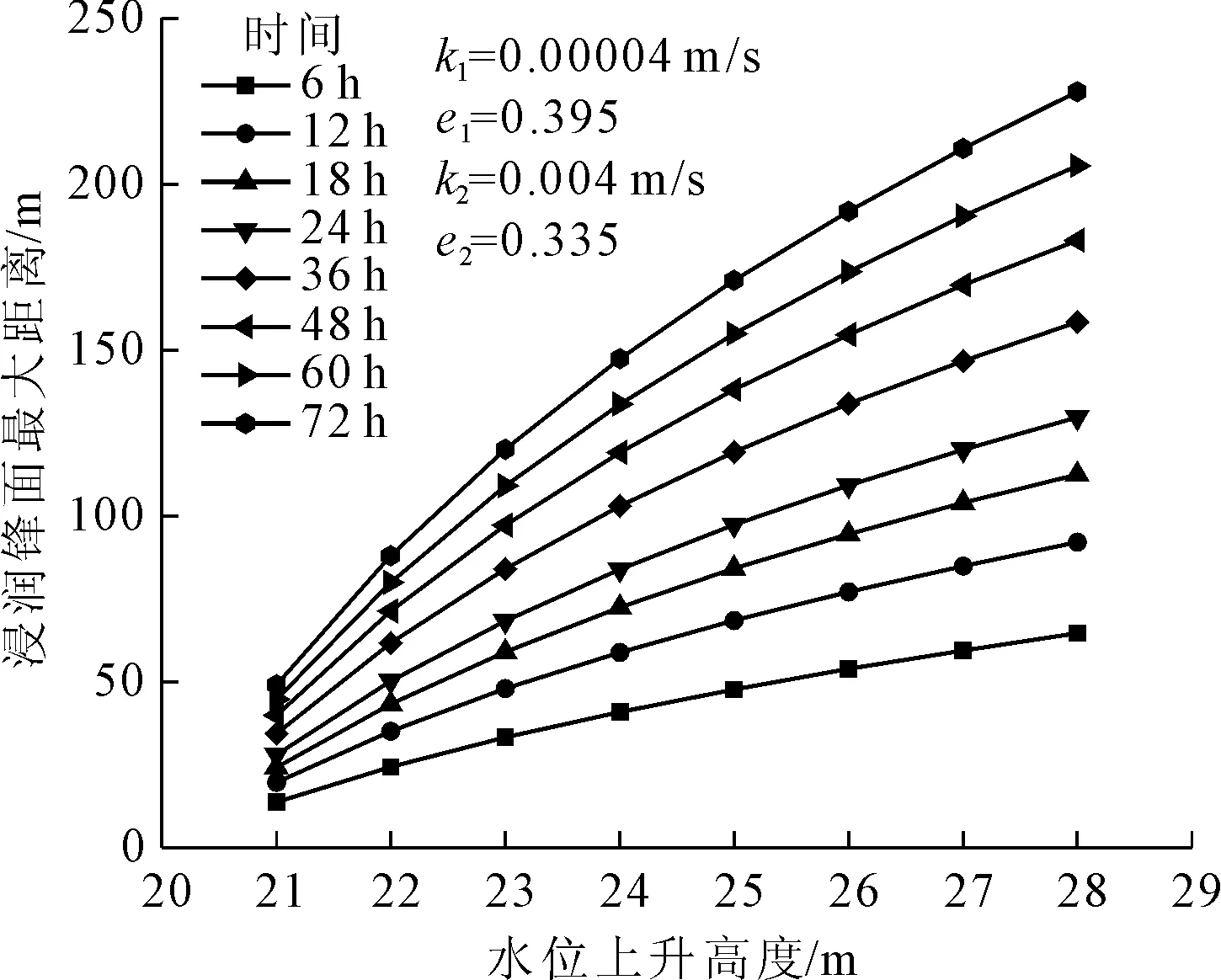
圖11 不同持續時間浸潤鋒面最大距離與水頭關系曲線

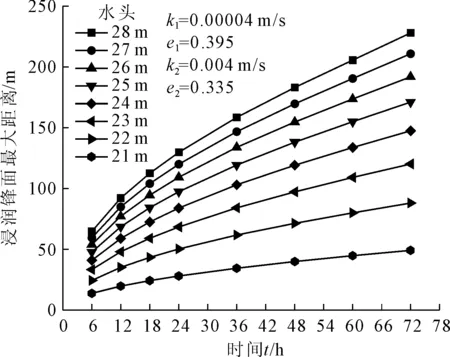
圖12 不同水頭浸潤鋒面最大距離與滲流時間關系曲線

由圖11和圖12可知，浸潤鋒面最大距離隨著水頭高度的增大呈上凸冪函數增長，同一水頭隨著滲透時間的增長，浸潤鋒面最大距離增長越慢。

4 影響浸潤鋒面最大距離的因素分析

由以上影響因素分析可知，浸潤鋒面最大距離的影響因素本次考慮如下六個因素：透水層滲透系數、初始水位、透水層厚度、水頭高度、坡率、滲流時間，每個影響因素都考慮5個水平，通過等水平正交試驗設計[14-15]，采用L25(56)等水平正交表進行試驗設計，利用極差分析法可以直觀簡便地分析實驗結果，確定因素的主次，極差越大，該因素對實驗結果的影響越大，正交試驗設計的因素及水平見表1。

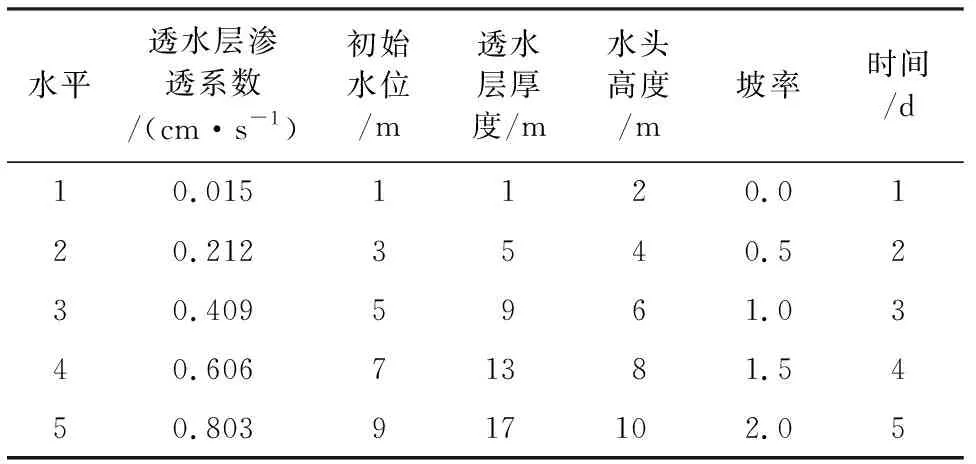
表1 正交試驗設計的因素及水平

依據正交設計和極差分析可知：各個因素對浸潤鋒面最大距離影響大小順序如下：水頭高度>透水層滲透系數>透水層厚度>滲流時間>坡率>初始水位。

5 結 論

(1) 浸潤鋒面最大距離的影響因素主要有透水層滲透系數、初始水位、透水層厚度、水頭高度、坡率、滲流時間六個影響因素。

(2) 浸潤鋒面最大距離受下部透水層的滲透系數控制，受上部半透水層的滲透系數影響很小；隨土層厚度增厚呈現先增大再減小最后趨于線性增長的趨勢；初始水位位于下部透水層范圍內時，浸潤鋒面最大距離隨初始水位增高呈指數增長趨勢，且滲流時間越長，浸潤鋒面最大距離增長越慢；隨著岸坡斜率的增大呈近線性增長，且增長的斜率基本不隨滲透時間變化；隨著水頭高度的增大呈冪函數增長，且隨著滲透時間的增長冪因素越來越大。

(3) 在未考慮復雜的水位變化過程的情況下，各個影響因素對浸潤鋒面最大距離影響大小順序河渠邊界如下：水頭高度>透水層滲透系數>透水層厚度>滲流時間>坡率>初始水位。