材料中帶有記憶項的隨機熱方程在薄域上的隨機吸引子

李 輝， 舒 級， 白欠欠， 李林妍

（四川師范大學 數學科學學院 可視化計算與虛擬現實四川省重點實驗室，四川 成都610066）

近年來，許多學者從不同的角度對薄域問題進行了廣泛的討論，用漸近展開、奇異攝動等方法研究了這類問題.確定耗散系統在薄域上的漸近行為的系統研究首先由Hale等［1］提出.后來他們的結果被大量引用［2］.除此之外，Chueshov 等［3］研究了薄域T2×（0，ε）上隨機3D Navier -Stokes 方程的遍歷性，其中T2為一個二維環面.Caraballo等［4］研究了一類半線性拋物型隨機方程組在薄有界管狀域內的同步問題.

設Q是Rn（n≥1）上光滑有界區域，Oε是如下定義的n+1 維區域：

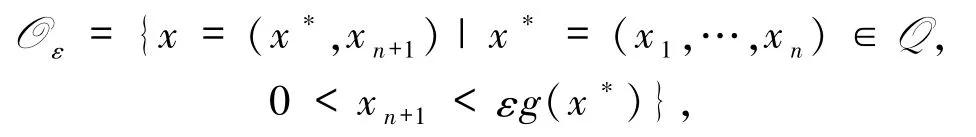
其中g∈C2（ˉQ，（0，+∞）），0 ＜ε≤1.易知存在正數r1、r2，使得對?x*∈ˉQ，有

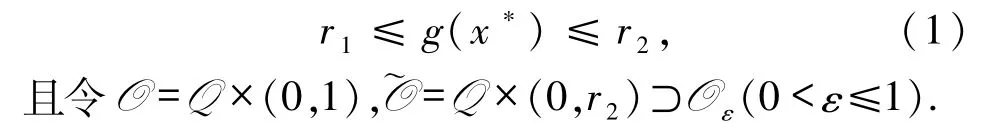
本文考慮薄域Oε上加性噪聲驅動的帶有記憶項的隨機熱方程

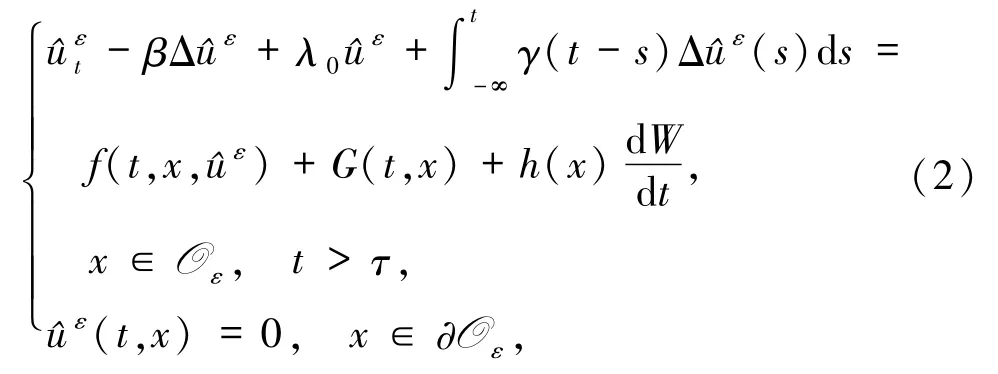
初值為

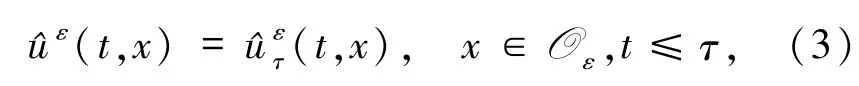
其中τ∈R，λ0，β ＞0，γ 是一個非負遞減的記憶核，是定義在?O ×R上的非負函數，h（x）∈C2（ˉQ ×［0，r2］），W是定義在概率空間上的雙邊實值Wiener 過程.s）Δ＾uε（s）ds是與＾uε有關的依賴過去歷史的擴散項.

眾所周知，方程（2）來源于帶記憶項的熱流理論［5］，它描述了一個依賴于溫度的反應過程.當γ=0，方程（2）不含記憶項，方程（2）簡化為帶噪聲的隨機拋物方程.在這種情況下，文獻［6 -7］中證明了隨機反應擴散方程的遍歷性和隨機吸引子的存在性.當不含噪聲時，方程（2）在文獻［8］中進行了一些討論.

由于隨機偏微分方程開始出現在各種各樣的應用中，需要考慮一些不確定性因素或隨機影響，它們被稱為噪聲.全局隨機吸引子的研究可以追溯到Ruelle的結果［9］.隨機系統的拉回吸引子的概念首先被文獻［10］引入，推廣了文獻［11］中確定性方程的全局吸引子.隨機偏微分方程的隨機吸引子已被許多學者討論，比如自治隨機方程［12-17］、非自治隨機方程［18-22］.最近，文獻［5］得到了一些關于帶有記憶項的隨機方程的隨機吸引子的結果.另外，文獻［23］證明了薄域上隨機反應擴散方程的隨機吸引子的存在性.然而在薄域上帶有記憶項的隨機方程卻很少有結果.受文獻［23 -24］的啟發，在本文中將研究方程（2）（3）的隨機拉回吸引子的存在性.為了在薄域Oε上處理方程（2）（3），需要轉換方程（2）（3）到一個固定區域O上.另一方面，由于記憶項包含了現象過去的全部歷史，無法證明其隨機動力系統的緊性，但是它的漸近緊性可以通過分解方法［8］來證明.

1 隨機動力系統

本節給出問題（2）（3）解的存在性和唯一性，并且該解在薄域Oε上能生成一個連續隨機動力系統.考慮如下方程

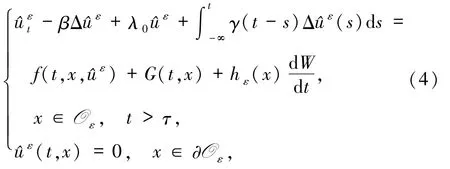
初值為

假設f滿足如下條件：對所有x∈?Q，＾uε∈R，

下面將方程（1）（2）轉化為區域O上的有界邊值問題.對?x=（x*，xn+1）∈Oε，定義變換：

對于上述薄域空間，引入新的函數空間并定義相關的內積與范數.首先賦予空間Hg（O）內積

現在考慮概率空間（Ω，F，P），其中Ω =｛ω∈C（R，R）：ω（0）=0｝，F 是由Ω 的緊開拓撲導出的Borel σ-代數，P是（Ω，F）上對應的Wiener 測度.這里規定W（t，ω）= ω（t），t∈R.定義時間平移算子

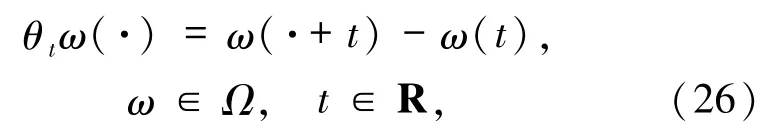
那么（Ω，F，P，｛θt｝t∈R）是一個度量動力系統.

給定ω∈Ω，令

2 解的一致估計

ω、ε、B無關的正常數.

證明將（28）式與vε在空間Hg（O）中做內積，有

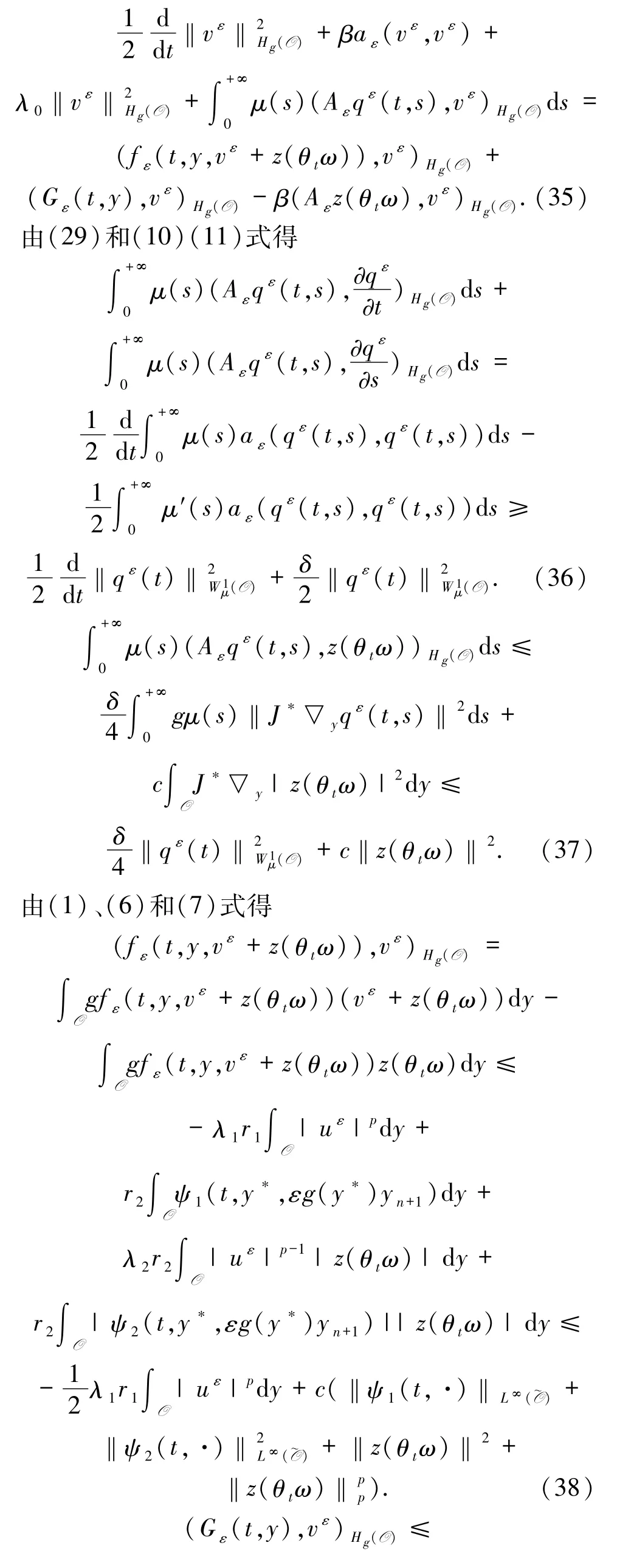
引理2.2假設（6）-（12）式成立，則存在ε0＞0，對?0 ＜ε ＜ε0，ω∈Ω，τ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在與ε 無關的T=T（τ，ω，B）＞1，使得對?t≥T，方程（28）-（31）的解滿足

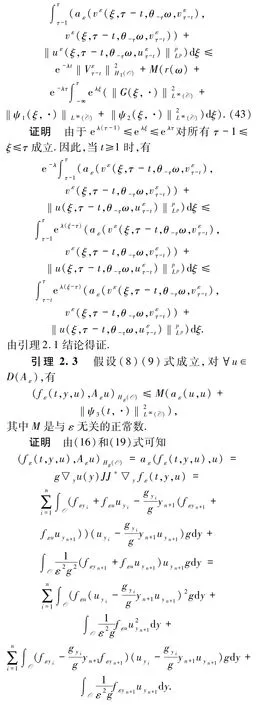
由（8）和（9）式可得

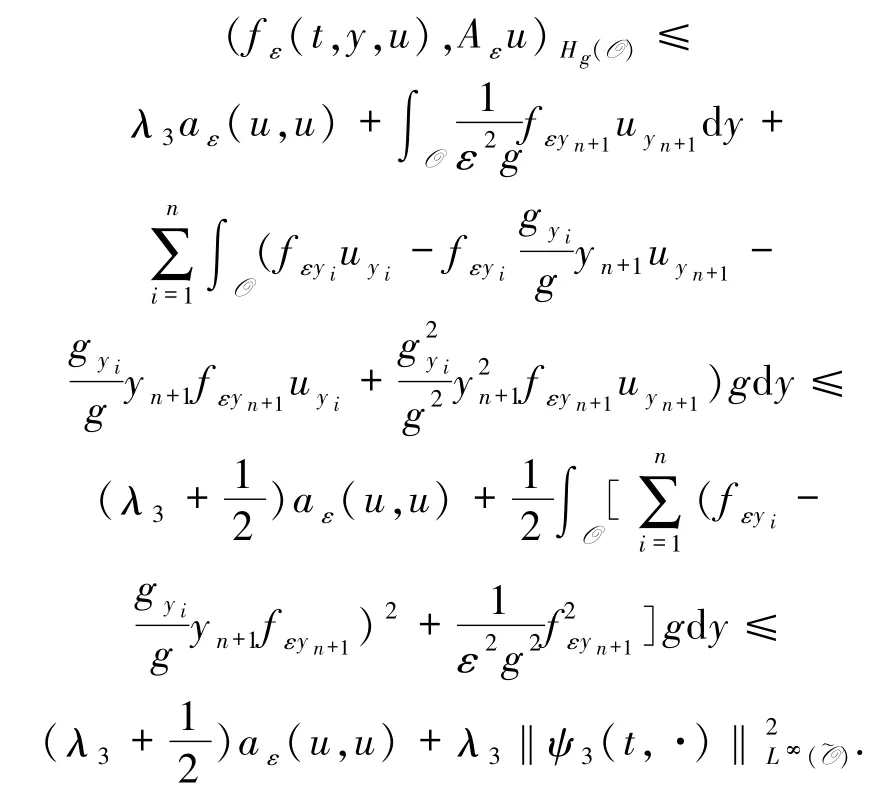
從而結論得證.

3 漸近緊性

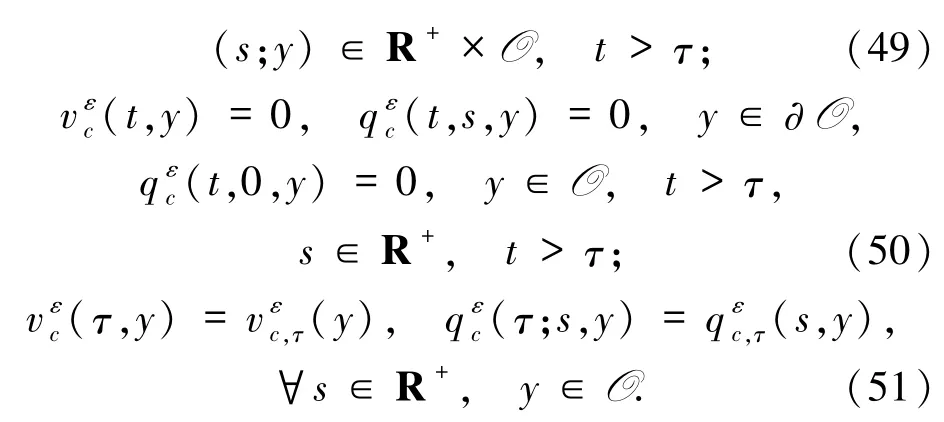
顯然，問題（44）-（47）和（48）-（51）的適定性可由Galerkin方法得到.

類似引理2.1 得

引理3.1假設（6）-（11）和（32）式成立，則存在ε0＞0，對?0 ＜ε ＜ε0，ω ∈Ω，τ ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在與ε 無關的T=T（τ，ω，B）＞0，使得對?t≥T，方程（44）-（47）的解滿足

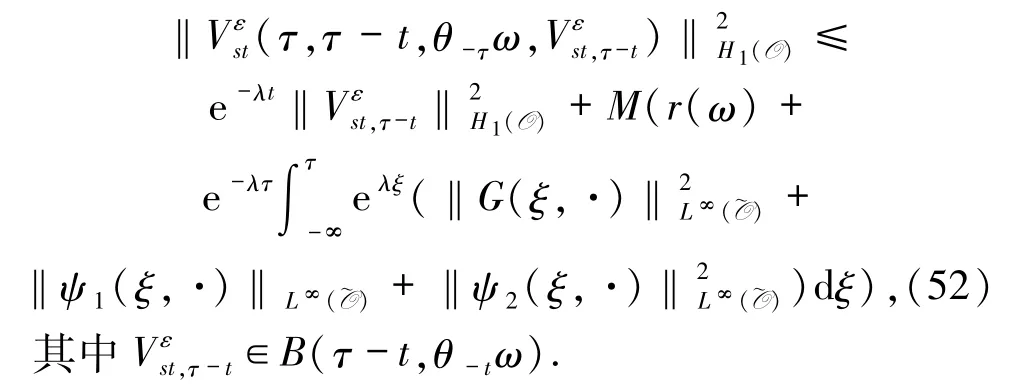
由引理3.1 易得：

引理3.2假設（6）-（11）和（32）式成立，則存在ε0＞0，對?0 ＜ε ＜ε0，ω ∈Ω，τ ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在與ε 無關的T=T（τ，ω，B）＞0，使得對?t≥T，方程（48）-（51）的解滿足

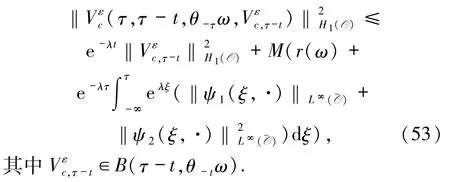
引理3.3假設（6）-（12）式成立，則存在ε0＞0，對?0 ＜ε ＜ε0，ω∈Ω，τ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在與ε無關的T=T（τ，ω，B）＞1，使得對?t≥T，方程（48）-（51）的解滿足

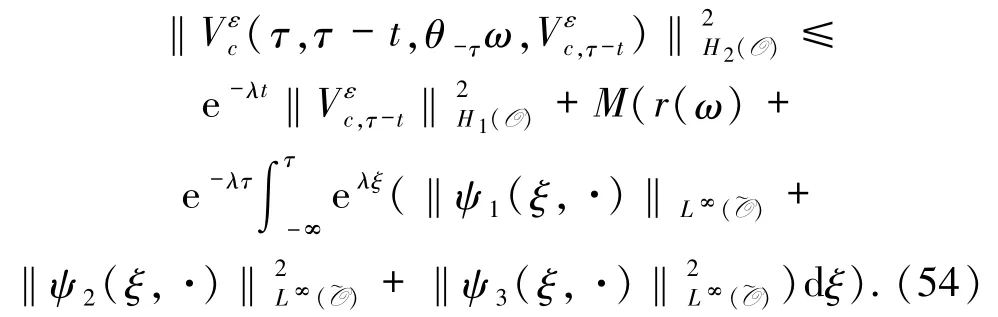
證明將（8）式與在空間Hg（O）中做內積，有

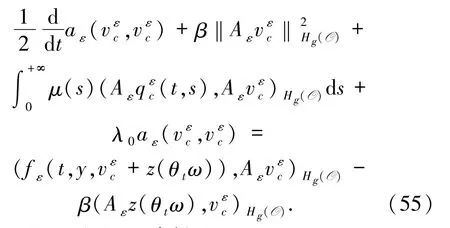
由（49）、（10）和（11）式得：

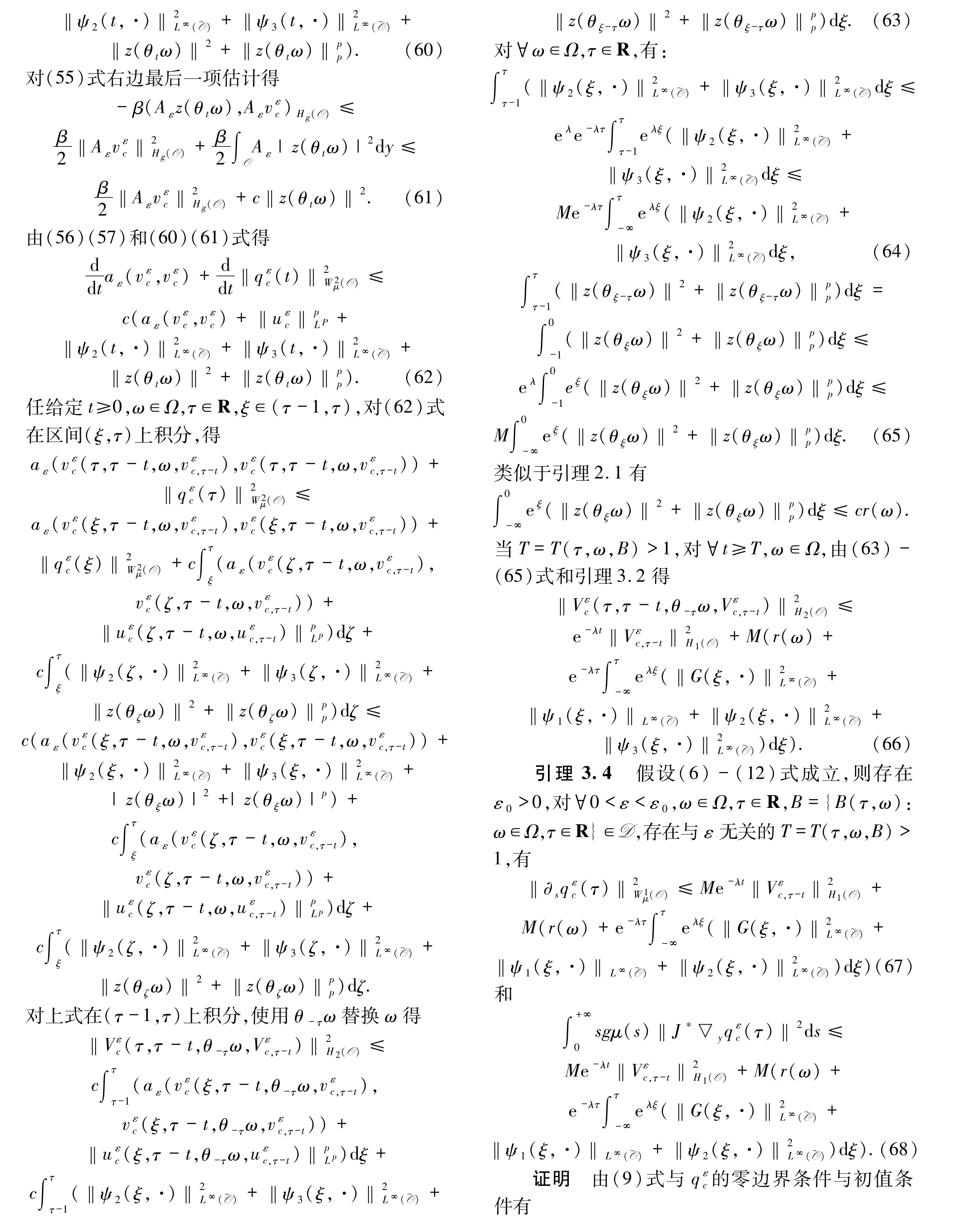
4 拉回吸引子的存在性

本節給出隨機方程（28）-（31）式對應的cocycle Φε的D1-拉回吸引子的存在性.

定理4.1假設（6）-（11）和（32）（33）式成立，則存在ε0＞0，對?0 ＜ε ＜ε0，cocycle Φε在空間H1（O）中存在唯一D1-拉回吸引子Aε=｛Aε（τ，ω）：ω∈Ω，τ∈R｝∈D1.

證明由引理3.5 和3.6、問題（28）-（31）生成的隨機動力系統在D1中是漸近緊的.因此，Φε存在唯一D1-拉回吸引子.

致謝可視化計算與虛擬現實四川省重點實驗室對本文給予了資助，謹致謝意.