一類含時滯和非線性擾動項的不確定隨機微分大系統的穩定性

易 玲， 李樹勇

（四川師范大學 數學科學學院，四川 成都610066）

含時滯的不確定隨機微分系統廣泛應用于物理、化學、生物學、工程等領域，由于時滯和隨機因素的影響，導致系統不穩定或震蕩，因而，含時滯的不確定隨機微分系統的穩定性分析受到學者們大量的關注，一系列的結果被建立［1-9］.通常，學者們用Lyapunov 泛 函 法［1-5］、Lyapunov - Razumikhin法［6］或線性矩陣不等式法（LMIs）［7-9］研究含時滯的隨機微分系統解的穩定性，然而Lyapunov泛函或函數構造較困難.因此，學者們致力于尋求其他的易于判別含時滯隨機微分系統穩定性的技巧.最近，Wang 等［10］利用非負矩陣、隨機卷積和不等式技巧研究了一類具有時滯的非線性隨機偏微分方程的穩定性，建立了這個系統解的吸引域和穩定性的判別定理.受他們思想的啟發，本文通過建立常數變易公式，利用非負矩陣性質和不等式技巧，研究一類含時滯和非線性擾動項的不確定隨機微分大系統的吸引性和穩定性，得到判斷這個系統吸引性和穩定性的充分條件，所得結果易于驗證且沒有要求非線性擾動項范數有界，擴大了穩定性的判別范圍.

1 基本準備

本文中，Rn表示n維的歐式空間，R表示n維非負的歐式空間. ?a∈Rn，定義‖·‖=I表示n×n維的單位矩陣，（Ω，F，P）是給定的完備概率空間，｛Ft｝t≥t0是（Ω，F，P）上給定的σ-代數流，滿足通常條件.w（t）是定義在其上的一維實值布朗運動，E（·）表示期望.對τ ＞0和正整數m，Cm?C（［-τ，0］，Rm）表示從［-τ，0］到Rm的連續函數空間，其上定義范數為‖φ‖τ=其中φ=（φ1，…，φm）T∈Cm.對p≥2，定義表示滿足E‖ζ‖p＜∞的Rm值F 可測的隨機過程ζ 的集合，Cm）表示滿足的Cm值F可測的隨機過程 的集合.分別定義范數

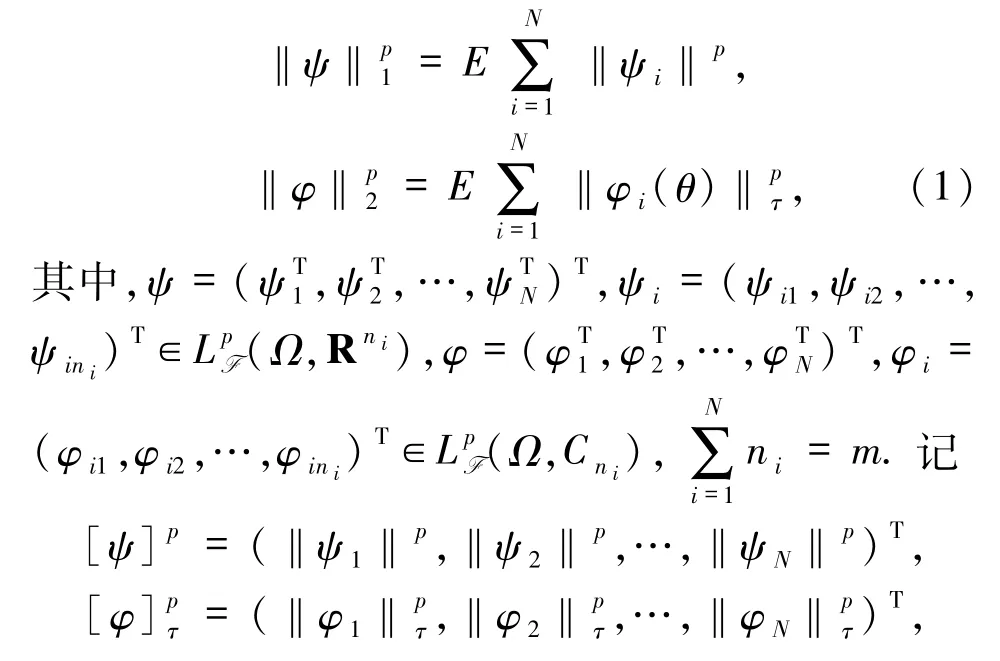
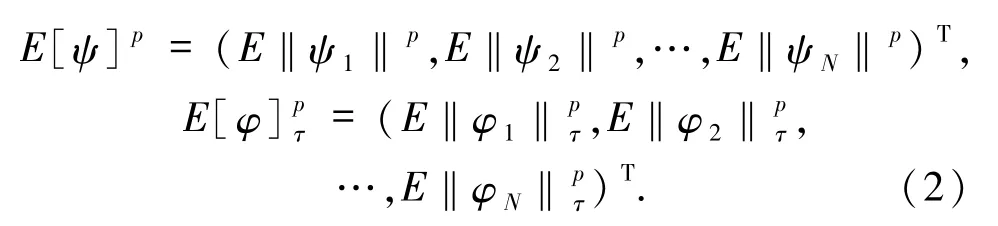
本文考慮含有時滯和非線性擾動項的不確定隨機微分大系統Σ，它由如下子系統Σi（i=1，2，…，N）組成：

定義1.3假設齊次泛函微分方程

其中，x∈Rm，L（t，xt）=A（t）x（t）+B（t）x（t-τ），A（t）和B（t）是m×m的連續矩陣函數.則稱矩陣Φ（t-s）是齊次方程（5）的基本解矩陣是指Φ（t-s）滿足

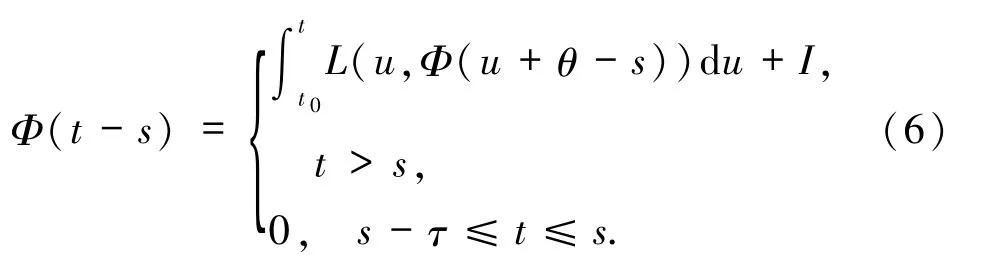
由文獻［11］的定理3. 1，方程（5）的基本解矩陣存在.

引理1.1［12］對于如下隨機微分系統

證明由（6）式，i=1，2，…，N，得

dΦi（t）=［Ai（t）Φi（t）+ Bi（t）Φi（t -τ）］dt.令ηi（t）=Φi（t）yi（t）（i=1，2，…，N），其中yi（t）滿足

與系統Σ對比，只需要證明

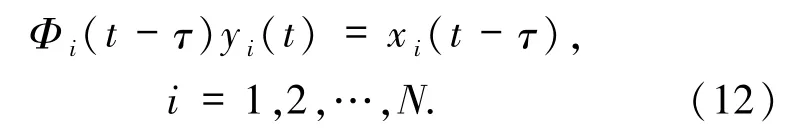
事實上，由（6）式有

Φi（t -τ- s）=0，s∈［t -τ，t］，所以

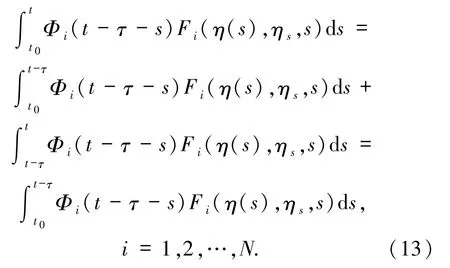
同理

因此

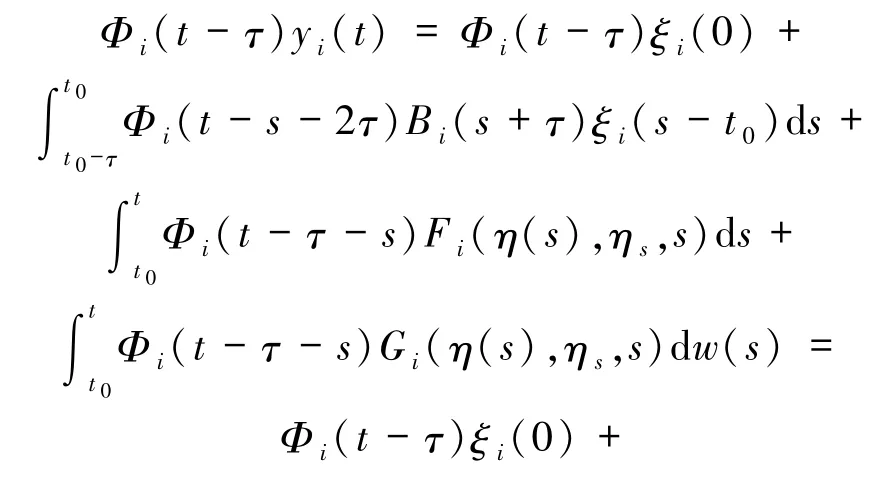
從而（12）式成立，即η（t）是系統Σ 的具有初始函數ξ的解.另一方面，由于系統Σ 的解唯一存在，所以x（t）=η（t），即（9）式成立.

2 主要結果

定理2.1對于系統Σ，假設：

（H1）存在向量函數H（φ）=（h1（φ），…，hN（φ））T和K（φ）=（k1（φ），…，kN（φ））T，且hi（φ），ki（φ）：RN+→R+是連續單調不減的凹函數，使得

（H2）設Φi（t）（i=1，2，…，N）是齊次方程（8）的基本解矩陣，滿足

并存在常數Mi≥1 和μi＞0 使得

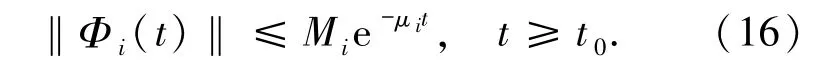
（H3）存在一個常向量z=（z1，…，zN）T≥0使得

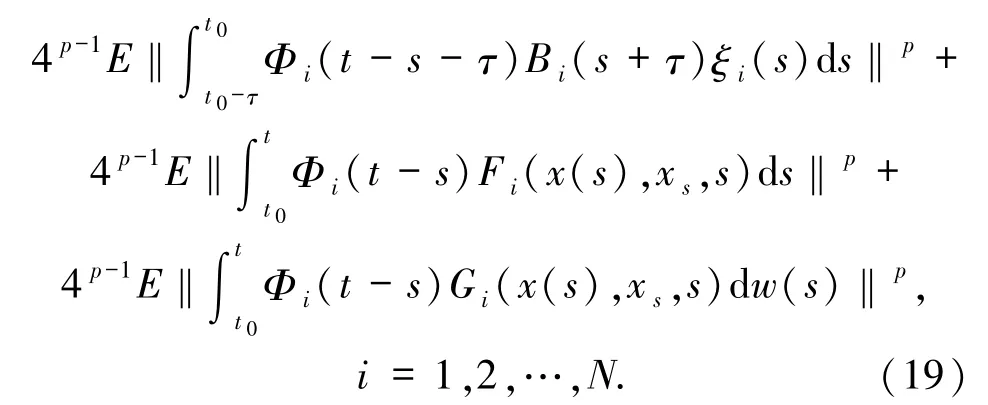
現在，對（19）式右邊分別進行估計.首先，由條件（H2）有

再次，由條件（H1）和（H2）、BDG不等式［12］和H?lder不等式有

與（28）式矛盾.因此，（27）式成立.令?→0，則（26）式成立.

定理2.2假設定理2.1 中所有條件成立.令向量函數

根據上極限的定義和（32）式，?? ＞0，?T1＞t0使得對任意的t≥T1，有

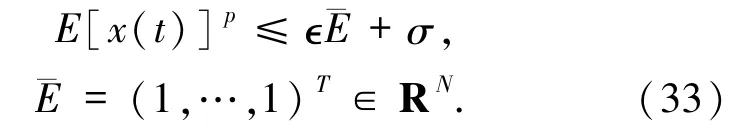
另一方面，由廣義積分性質的定義，?T2＞t0使得

（35）式兩邊求上極限得

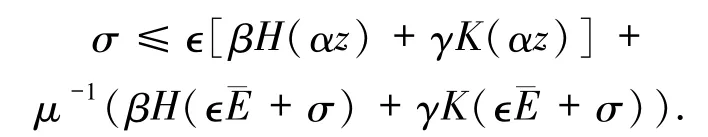
令?→0+，則

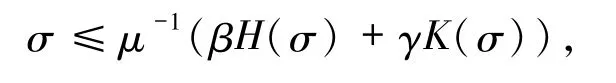
所以Ξ（σ）≥0，σ∈Ω0，即S是系統Σ 的p-階矩吸引集.

由函數Ξ（y）的定義，易知集合

3 例子

例3.1考慮如下的一維時滯的隨機不確定微分方程

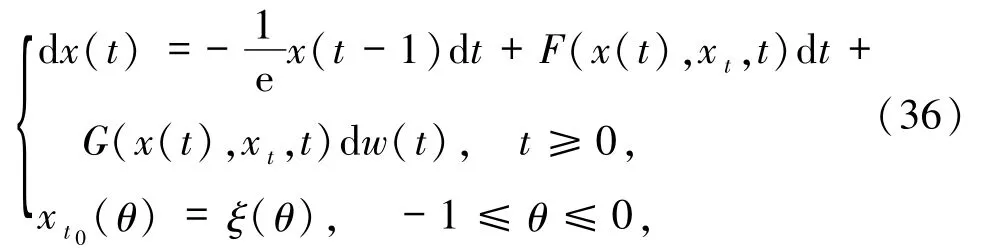
其中，xt（θ）=x（t+θ），-1≤θ≤0.

假設F和G滿足

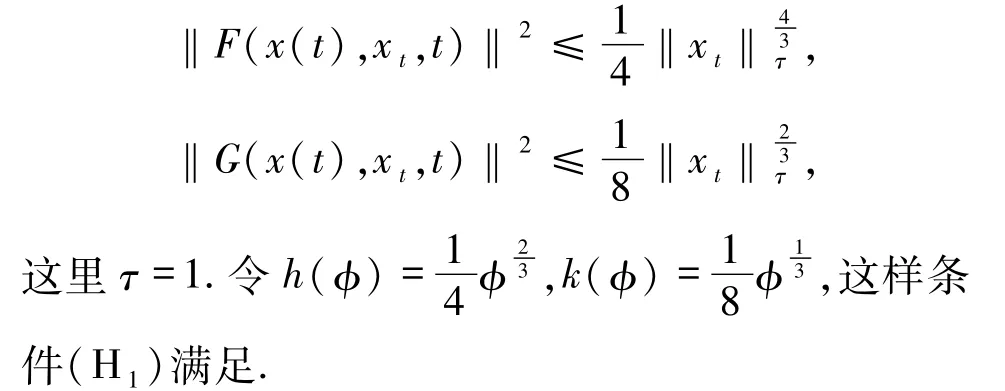
因為齊次確定方程

所以有Ξ（y）=（Ξ1（y），Ξ2（y））T，其中