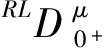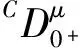一類具有非局部條件的Sobolev型Hilfer分數階發展方程的偏近似可控性
王星昭,顧海波
(新疆師范大學 數學科學學院,新疆 烏魯木齊 830017)
可控性問題是控制系統的重要問題,在許多工程問題中起到至關重要的作用,例如使用反饋控制可以使不穩定的系統穩定化。可控性大致可分為精確可控性和近似可控性,對兩者進行區分是非常有必要的:若系統是精確可控的,我們可以控制系統到一個任意的最終狀態;而若系統是近似可控的,則只能控制系統到一個任意最終狀態的任意小的鄰域內。通常,精確可控性比近似可控性要求的條件更加苛刻,而在大多數情況下,近似可控性已經可以滿足我們的需求,因此近似可控性在實際中應用更為廣泛。近幾年,有大批學者研究了多種不同類型的分數階動力系統的近似可控性問題,已有很多關于近似可控性的研究成果。例如,Kerboua等[1]研究了Hilbert空間中一類帶有Caputo分數階導數的Sobolev型隨機發展方程的近似可控性,方程具有非局部條件;Mahmudov等[2]研究了Hilbert空間中一類帶有Hilfer分數階導數的發展方程的近似可控性;Ge等[3]用近似法,研究了Banach空間中一類帶有Caputo分數階導數的發展方程的近似可控性,方程具有非局部條件和脈沖條件;Chang等[4]利用預解算子的性質,研究了Banach空間中兩類Sobolev型發展方程的近似可控性,一類帶有Caputo分數階導數,一類帶有Riemann-Liouville分數階導數;Mahmudov[5]用近似法和變分法,分別研究了Hilbert空間中一類帶有Caputo分數階導數的發展方程的偏近似可控性和有限近似可控性[6],方程具有非局部條件;He等[7]研究了Hilbert空間中一類帶有Riemann-Liouville分數階導數的隨機波動方程的近似可控性;Huang等[8]研究了Banach空間中一類帶有Caputo分數階導數的拋物方程的近似可控性;Mokkedem[9]研究了一類帶有Riemann-Liouville分數階導數的微分方程的近似可控性,方程具有無窮時滯;Jeet等[10]用近似法研究了一類中立型微分方程的近似可控性,方程具有非局部條件和脈沖條件;Anguraj等[11]研究了一類具有Poisson跳躍的隨機微分方程的近似可控性,方程具有非局部條件和脈沖條件。
然而,具有非局部條件的Sobolev型Hilfer分數階發展方程的偏近似可控性研究還未見報道。我們在沿用Mahmudov[5]方法的基礎上,對其控制系統進行了推廣,將Caputo分數階導數推廣為Hilfer分數階導數,將發展方程推廣成Sobolev型的。
更具體地,我們研究了如下一類分數階發展方程的偏近似可控性:
(1)

本文在研究系統(1)的偏近似可控性時,非局部項g并不滿足Lipschitz條件。此外,為得到控制系統解的存在性,我們構造了控制系統的近似解算子,并證明了近似解集的緊性,將解的存在性問題轉化為一個不動點序列問題。這與傳統的方法(將不動點定理直接應用于相應的解算子)是不同的。
1 預備知識
我們回顧一些符號、定義,以及分數階導數和分數階微分方程方面的結果。

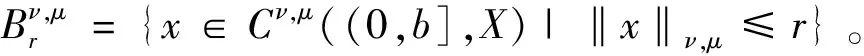
定義1[12]函數f:[0,+∞)→R的下限為0,階為μ的分數階積分為:
假設右側是逐點定義在[0,+∞)上的,R表示實數,Γ(·)是伽馬函數。
定義2[13]函數f:[0,+∞)→R的下限為0,階為ν∈[0,1]和μ∈(0,1)的Hilfer分數階導數為:
其中函數需使得右側的表示存在。
定義3[1,6,14]如果函數x∈C((0,b],X)滿足方程:
(2)
則x是(1)的一個適度解。其中
且ωμ(θ)滿足
(3)
引理1[1,14-15]算子Pν,μ和Qμ具有以下性質:
(i){Pν,μ(t)|t∈(0,+∞)}和{Qμ(t)|t∈(0,+∞)}是強連續的;
(ii)如果{S(t)|t∈(0,+∞)}是緊的,則{Pν,μ(t)|t∈(0,+∞)}和{Qμ(t)|t∈(0,+∞)}是緊算子;
(iii)對任意固定的t∈(0,+∞),Pν,μ(t)和Qμ(t)是線性算子,且對任意的x∈X,有
(4)
定義4[16]給定b∈(0,+∞),x0∈X,xb∈E,如果對任意的ε∈(0,+∞),總存在一個控制uε∈L2([0,b],U),使得(1)對應的解x(t;uε)滿足條件
‖Ξx(b;uε)-xb‖<ε,
則系統(1)在(0,b]上是偏近似可控的。
注記1特別地,當E=X時,偏近似可控性概念與近似可控性概念一致。
2 主要結果
在本文中,我們給出以下假設:
(H1)S(t),t∈(0,+∞)是緊算子;
(H2)對每個t∈[0,b],函數f(t,·):X→X是連續的,且對每個x∈X,函數f(·,x):[0,b]→X是強可測的;
(H3)存在一個正連續函數n∈C([0,b],R+),使得對任意的(t,x)∈[0,b]×X,都有
‖f(t,x)‖≤n(t);
(H4)函數g:C((0,b],X)→X是連續的,且存在一個正常數Λg,使得對任意的x∈X,都有
‖g(x)‖≤Λg;
(H5)存在δ∈(0,b),使得對任意的x,y∈C((0,b],X),都有
x(t)=y(t),t∈[δ,b],
g(x)=g(y);
(H6)線性分數階微分系統
(5)
在(0,b]上是偏近似可控的。

對任意的ε∈(0,+∞),n=1,2,3,…,定義泛函
(6)
其中
(7)
并定義算子Q:Cν,μ((0,b],X)→E如下:
=Q1(x)+Q2(x)。
(8)
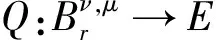
證明見本文OSID開放科學數據與內容。
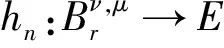
證明見本文OSID開放科學數據與內容。
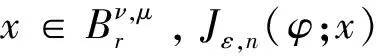
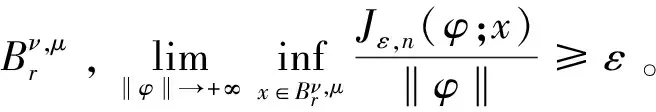
證明見本文OSID開放科學數據與內容。

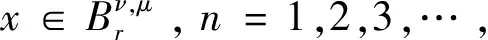
證明見本文OSID開放科學數據與內容。
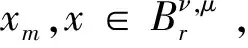
證明見本文OSID開放科學數據與內容。
對任意的ε∈(0,+∞),n=1,2,3,…,定義算子Θε,n:Cν,μ((0,b],X)→Cν,μ((0,b],X)如下:
(9)
根據式(3)可得
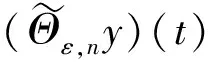
(10)
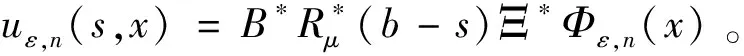
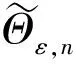
證明見本文OSID開放科學數據與內容。

證明見本文OSID開放科學數據與內容。
對任意的ε∈(0,+∞),t∈(0,b],定義(Θεx)(t)如下:
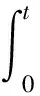
(11)

(12)
(13)
在Cν,μ((0,b],X)中的一個適度解。
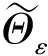
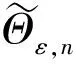
我們定義近似解集D如下:

對任意的yε,n∈D,n=1,2,3,…,定義
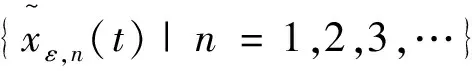
由假設(H5)可得
由S(t)和g的連續性,當n→+∞時,
故D(0)在X中是相對緊的。
(ii)對任意的t∈(0,b],集合D(t)={yε,n(t)|n=1,2,3,…}在X中是相對緊的。
(iii)D在t=0處是等度連續的。

故集合D在t=0處是等度連續的。
(iv)D在(0,b]上是等度連續的。
對任意的yε,n∈D,0 =I1+I2+I3+I4。 由假設(H4)及Pν,μ(t),t∈(0,+∞)的強連續性,對任意的yε,n∈D,當t2→t1時, 當t2→t1時, 當t2→t1時, 選取η∈(0,+∞),使得t1-η∈(0,+∞),由Rμ(t),t∈(0,+∞)的連續性,當t2→t1,η→0時, 綜上,集合D在(0,b]上是等度連續的。 因此集合D在C([0,b],X)中是相對緊的。故可以假設:當n→+∞時, yε,n→yε∈C([0,b],X), 則由引理7得,uε,n(s,xε,n)→uε(s,xε)。 由定理2知,控制系統(13)有解xε,即對任意的ε∈(0,+∞),存在xε∈Cν,μ((0,b],X),使得 定理3 若假設(H1)~(H6)成立,則系統(1)在(0,b]上是偏近似可控的. 故對任意的τ∈R,ψ∈X,有 (14) 當τ∈(0,+∞)時,式(14)兩邊同除以τ得 令τ→0+可得 (15) 當τ∈(-∞,0)時,也進行類似的討論,可得 (16) 結合式(15)、(16)有 (17) 注意到 故 (18) 結合式(17)、(18)可得 |〈Ξxε(b)-xb,ψ〉|≤ε‖ψ‖。 (19) 由式(19)可得 ‖Ξx(b;uε)-xb‖<ε, 即系統(1)是偏近似可控的。 我們最終得到了控制系統(1)在(0,b]上偏近似可控的充分條件,即假設(H1)~(H6)成立。本文的研究結果比相關問題的現有成果更具一般性。事實上,以下兩類經典的分數階發展方程是本文所研究的分數階發展方程的特例: 當算子C=I為恒等算子,階數ν=0時,系統(1)變為 (20) 當算子C=I為恒等算子,階數ν=1時,系統(1)變為 (21)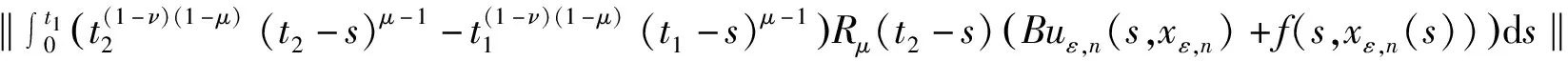
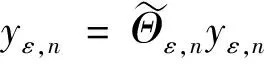



3 結論