為什么點(diǎn)那么難“描”

阮萍揚(yáng)

(福建省泉州師范學(xué)院附屬中學(xué) 福建 泉州 362000)

建系法是解決高中理科立體幾何問(wèn)題的一種有效方法，模式化也比較明顯，在完成建系和描點(diǎn)后，套入公式一般都可以解決問(wèn)題，這類問(wèn)題有較為明顯的“套路解法”，照理學(xué)生的得分率要很高，但實(shí)踐過(guò)程中筆者卻發(fā)現(xiàn)情況截然相反。究其原因，其中一個(gè)主要的問(wèn)題是學(xué)生不會(huì)描點(diǎn)，為什么點(diǎn)那么難描？可能是一些描點(diǎn)的“技巧”沒(méi)有掌握好。

1.選擇合適的空間直角坐標(biāo)系

例題1:如圖1，在四棱錐P-ABCD中，底面ABCD是邊長(zhǎng)為1的菱形，∠BAD=45°,PD=2,若平面PDC⊥底面ABCD，且PD⊥DC，求平面PAD與平面PBC所成銳二面角的余弦值。

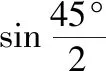
2.從空間向量角度進(jìn)行描點(diǎn)

例題2:(2014課標(biāo)1)如圖5，三棱柱ABC-A1B1C1中，側(cè)面BB1C1C為菱形，AB⊥B1C。(1)證明：AC=AB1；(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A-A1B1-C1的余弦值。

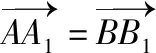
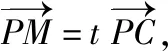
3.題目中核心信息遺漏

例題4:(2018課標(biāo)1)如圖9，四邊形ABCD為正方形，E,F分別為AD,BC的中點(diǎn)，以DF為折痕把△DFC折起，使點(diǎn)C到達(dá)點(diǎn)P的位置，且PF⊥BF。(1)證明：平面PEF⊥平面ABFD；(2)求DP與平面ABFD所成角的正弦值。

解析:過(guò)點(diǎn)P做EF的垂線，交EF于點(diǎn)O,即PO⊥面ABCD。如圖10建立空間直角坐標(biāo)系，設(shè)AB=2，瞬間發(fā)現(xiàn)，所有的坐標(biāo)都很難求。這是因?yàn)橛幸粋€(gè)核心信息遺漏了！遺漏了什么信息呢？遺漏了PF⊥面PED，就有PF⊥PE！這里△EPF是直角三角形！有了這個(gè)信息，那么描點(diǎn)就非常容易了！這樣的命題手法非常高明，對(duì)學(xué)生來(lái)說(shuō)是一個(gè)挑戰(zhàn)，如果沒(méi)有對(duì)信息進(jìn)行再挖掘，僅僅通過(guò)表象信息去解決問(wèn)題，往往無(wú)功而返耗時(shí)耗力。這給了我們一個(gè)提示，描點(diǎn)遇到障礙時(shí)，認(rèn)真細(xì)讀題目給出的信息，對(duì)信息進(jìn)行二次挖掘，把隱藏的結(jié)論揭示出來(lái)，問(wèn)題便迎刃而解。

總結(jié)

建系、描點(diǎn)、套公式，這是立體幾何建系法的三步驟。描點(diǎn)成為最關(guān)鍵的一步。除了傳統(tǒng)的將點(diǎn)投影到坐標(biāo)平面或投影到坐標(biāo)軸外，其實(shí)，我們還有一些“小技巧”、“補(bǔ)充結(jié)論”和“解題經(jīng)驗(yàn)”來(lái)幫助建系和描點(diǎn)。